Math and learning from data
Zhi Han
"Suppose that you want to teach the 'cat' concept to a very young child. Do you explain that a cat is a relatively small, primarily carnivorous mammal with retractible claws, a distinctive sonic output, etc.? I'll bet not. You probably show the kid a lot of different cats, saying 'kitty' each time, until it gets the idea. To put it more generally, generalizations are best made by abstraction from experience."
R. P. Boas (Can we make mathematics inelligible?, American Mathematical Monthly 88 (1981), pp. 727-731)
Summary
- Two algorithms
- Math and learning from data
- Implications
This talk is partly an adaptation of the YouTube series "Learning to See" by Welch Labs.
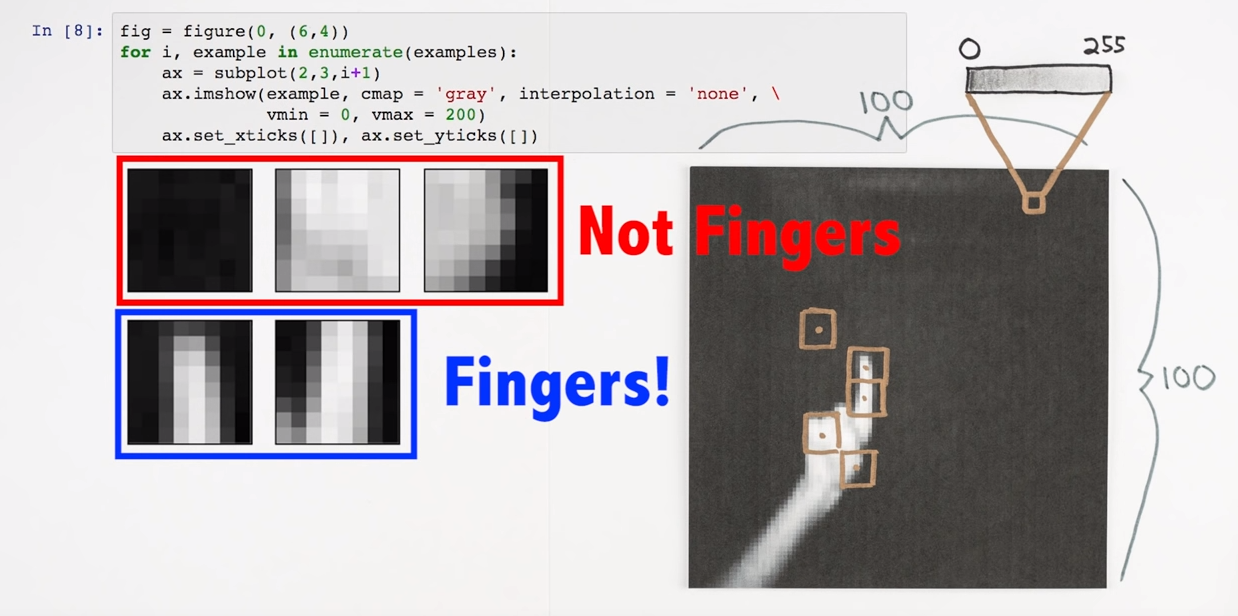
Counting fingers
Imagine we want to teach a machine how to count fingers.
After all, counting is the foundation of arithemetic. How might we do this?

Knowledge Engineering
We could just define what a finger looks like:

Knowledge Engineering
Testing the algorithm, we see:

Knowledge Engineering
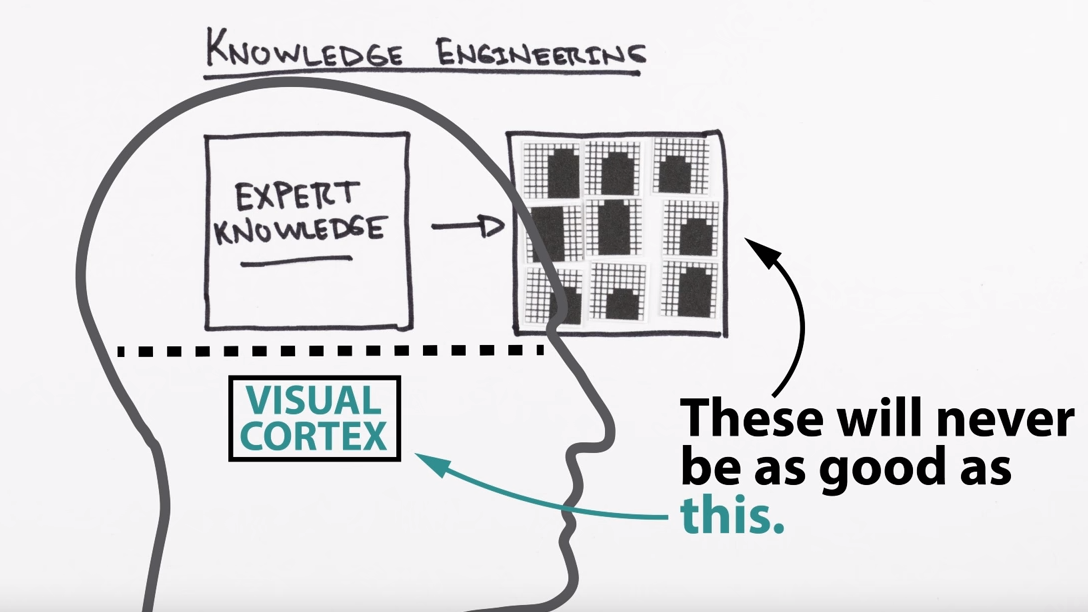
Could just keep adding rules on top of rules on top of rules, but:
- Database is tedious to maintain
- Can't recognize other objects
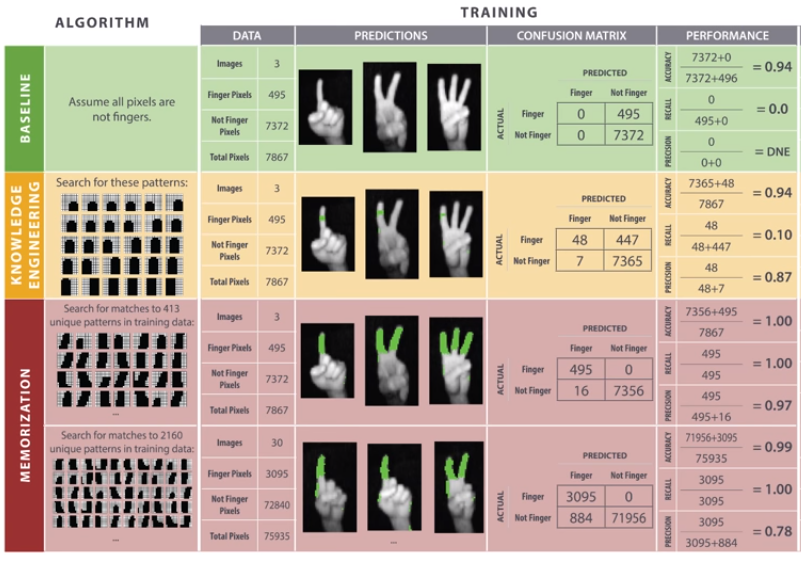
Memorization
Fine. We can't define what a finger looks like, so let's take the training examples to be rules:

Memorization
On the training data, it performs well!
Knowledge engineering: 10%
Memorization: 100%
Memorization
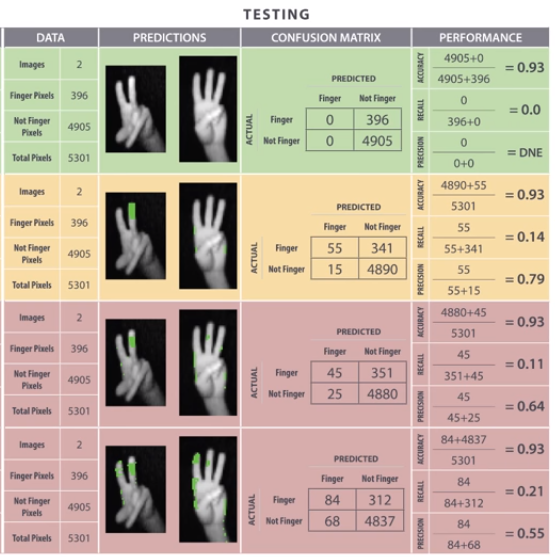
On the test set, not so well:
Knowledge engineering: 14%
Memorization: 11%
Memorization with 10x the examples: 21%
Incoming Feynman quote...

To learn is to generalize
Futility of bias free learning
We saw in our two algorithms, memorization and knowledge engineering that
- Knowledge engineering (maximum assumptions)
- Memorization (zero assumptions)
perform poorly on the testing phase.
- Data alone is not enough to determine a unique answer.
- Turns out, to generalize, need to make assumptions.
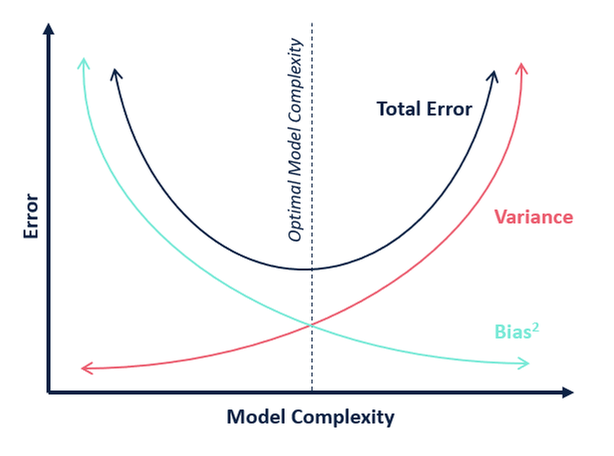
The bias variance trade off.
Futility of Bias Free Learning
In statistics, data is non-biased. This implies that:
- Machine learning is an ill-posed problem. There is no best answer.
How do we learn?
Lessons from Machine Learning
To learn is to generalize.
To learn from data, we have to make assumptions on the data.
What is the data?
Math as a learning process
Intuition
"data"
Formalism
"generalizations"
- physical world
- conjectures
- open problems
- questions
- math itself
- theorems
- axioms
- definitions
- frameworks
Proof
Abuse of notation
Child
Mathematician


Summary of the talk.
Math as a learning process
To learn from data, we have to make assumptions on the data.
Why might we prefer some axiomatic systems over others?
Suggests that math is grounded in human intuition.
Human intuition as foundations
- Explains why:
- Why we might prefer some axiomatic systems over others
- Why the axioms must be true
- Why the child and mathematician are different: learning
- Engineers don't need to know abstract math
- Children intuitively know what numbers are.
- Generalizations of the same math can lead to different results
- Different notations and interpretations
- Why we might prefer some axiomatic systems over others
- Problems:
- Non-objective, different between mathematicians
- Not rigorous.
- But the formalization of intuition is rigourous! This is what math is all about!
Conclusion
- Mathematics is about generalizing things in a rigorous way.
- Really a learning process
- Generalizing from data (human intuition)
- The physical world is the best axiom
- A good argument for structuralism.