递归

什么是递归

在计算机科学中，递归是一种方法，其中问题的解决取决于相同问题的较小实例的解决方案（与迭代相对）。

如何解决问题

将问题分解为小问题。
解决小问题。
使用小问题的结果来解决原始问题。
如果小问题与原问题相同，只是规模不同，则称为递归。

递归的属性

基本情况
- 指不需要递归即可得出答案的简单情况。
递归
- 是一组规则，将所有其他情况都归纳到基本情况下。

使用递归解决编程问题

基本情况
递归规则
使用编程函数表示问题
- 定义必要的参数
  - 定义问题的参数
  - 存储临时结果或状态的参数
- 定义返回值

斐波那契数列
- 可以使用动态规划解决，效果更好
爬楼梯
- 与斐波那契数列类似
归并排序
- 我们将在排序中详细讨论
汉诺塔
二分查找
- 这是一种只有一个递归调用的递归，因此可以使用迭代来实现

经典递归问题

问题

子问题1

基础问题

子问题2

子问题3

子子问题2

子子子问题

子子问题1

...

问题

子问题1

子子问题

子子子问题

基础问题

问题

子问题1

基础问题

子问题2

子问题3

子子问题2

子子子问题

子子问题1

...

问题

子问题1

子子问题

子子子问题

基础问题

问题

子问题1

基础问题

子问题2

子问题3

子子问题2

子子子问题

子子问题1

...

问题

子问题1

子子问题

子子子问题

基础问题

问题

子问题1

基础问题

子问题2

子问题3

子子问题2

子子子问题

子子问题1

...

问题

子问题1

子子问题

子子子问题

基础问题

问题

子问题1

基础问题

子问题2

子问题3

子子问题2

子子子问题1

子子问题1

...

问题

子问题1

子子问题

子子子问题

基础问题

问题

子问题1

子子问题

子子子问题

基础问题

问题

子问题1

基础问题

子问题2

子问题3

子子问题2

子子子问题

子子问题1

...

回溯

单子问题递归

单一子问题递归并不一定非要使用递归来解决

我们可以使用迭代的方式来解决这种问题

它也不是动态规划

int Factorial(int n， int total) {
    if(n == 1) return 1;
    return n * Factorial(n-1, n * total);
}

int Factorial(int n) {
    int sum = 1;
    for(int i = 1; i <= n; i ++) {
        sum = sum * i;
    }
    return sum;
}

格雷码

格雷码是一种二进制数码系统，在该数码系统中，两个相邻的数值仅有一位二进制数不同。

给定一个非负整数 n 表示码中总位数的数量，请输出其格雷码序列，序列必须以 0 开始。

例如，给定 n = 2，返回 [0,1,3,2]。

这是一个典型的单一子问题问题，需要在问题内部找到模式

格雷码

格雷码是一种二进制数码系统，在该数码系统中，两个相邻的数值仅有一位二进制数不同。

给定一个非负整数 n 表示码中总位数的数量，请输出其格雷码序列，序列必须以 0 开始。

例如，给定 n = 2，返回 [0,1,3,2]。

n=2

n=3

对称

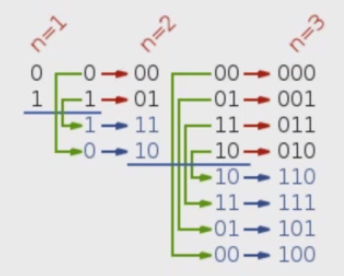
格雷码

public List<Integer> grayCode(int n) {
    List<Integer> result = new ArrayList<>();
    helper(n, result);
    return result;
}
public void helper(int n, List<Integer> result) {
    if (n == 0) {
       result.add(0);
       return;
    }
    helper(n-1, result);
    int size = result.size();
    int k = 1 << (n - 1);
    for (int i = size - 1; i >= 0; i --) {
        result.add(result.get(i) + k);
    }
    return;
}

关键在于找到每个子问题之间的关系

格雷码

public List<Integer> grayCode(int n) {
    List<Integer> result = new ArrayList<>();
    result.add(0);
    for(int i = 0; i < n; i ++) {
        int k = 1 << i;
        int size = result.size();
        for(int j = size - 1; j >= 0; j --) {
            result.add(result.get(j) + k);
        }
    }
    return result;
}

实际上，这也是一种尾递归。我们实际上可以摆脱递归代码。

0-1背包

给定一个能够容纳 s 磅物品的背包和一组具有重量 w1，w2，... wn 的物品。返回是否可以选择特定物品，使它们的总重量为 s。

示例输入：

s = 20;

w = [14, 8, 7, 5, 3];

示例输出：

True；

对于每个物品，我们只有两个选择:

把它放进背包，然后问题就转化成了 (s-w[i], w - w[i])
不把它放进背包，那么问题就转化成了 (s, w - w[i])

0-1 背包

假设有一个可容纳重量为s磅的背包，还有一组物品，它们的重量分别为w1、w2、...wn。编写一个函数来判断是否可以选取特定的物品，使它们的总重量恰好为s。

public boolean knapsack(int s, int[] weights) {
    return knapsack(s, weights, 0);
}

public boolean knapsack(int s, int[] weights, int index) {
	
    if (s == 0) {
      return true;
    }
    if (s < 0 || index == weights.length) {
      return false;
    }
    return knapsack(s - weights[index], weights, index+1) ||
      knapsack(s, weights, index+1);
}

在权重中添加/删除元素是困难的，因此可以添加一个索引，并移动索引

考虑到返回的两个值，它们的顺序是否重要？

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

示例输入：

起点: (0, 0); 终点 (5, 5);

迷宫: char[][] = {

{'.', 'X', '.', '.', '.', 'X'},

{'.', '.', '.', 'X', '.', 'X'},

{'X', 'X', '.', 'X', '.', '.'},

{'.', 'X', 'X', 'X', '.', 'X'},

{'.', '.', '.', '.', '.', 'X'},

{'.', '.', '.', '.', '.', '.'}

}

示例输出: True

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

示例输入:

起点: (0, 0); 终点 (5, 5);

迷宫: char[][] = {

{'.', 'X', '.', '.', '.', 'X'},

{'.', '.', '.', 'X', '.', 'X'},

{'X', 'X', '.', 'X', '.', '.'},

{'.', 'X', 'X', 'X', '.', 'X'},

{'.', '.', '.', '.', '.', 'X'},

{'.', '.', '.', '.', '.', '.'}

}

示例输出: True

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

越界
墙壁

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

越界
墙壁
已访问
- (1, 2) -> (2, 2) -> (1, 2) -> (2, 2) -> ...

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

public static boolean solveMaze(char[][] maze, 
                                int startX, int startY, int targetX, int targetY,
                                boolean[][] visited) {
    if (startX < 0 || startX >= maze.length ||
        startY < 0 || startY >= maze[0].length ||
        maze[startX][startY] == 'X' || visited[startX][startY]) {
      return false;
    }
    if (startX == targetX && startY == targetY) {
      return true;
    }
    visited[startX][startY] = true;
    if (solveMaze(maze, startX + 1, startY, targetX, targetY, visited) ||
        solveMaze(maze, startX, startY + 1, targetX, targetY, visited) ||
        solveMaze(maze, startX - 1, startY, targetX, targetY, visited) ||
        solveMaze(maze, startX, startY - 1, targetX, targetY, visited)) {
      return true;
    }
    return false;
}

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

public static boolean solveMaze(char[][] maze, 
                                int startX, int startY, int targetX, int targetY) {

    if (startX < 0 || startX >= maze.length ||
        startY < 0 || startY >= maze[0].length ||
        maze[startX][startY] == 'X') {
      return false;
    }
    if (startX == targetX && startY == targetY) {
      return true;
    }
    maze[startX][startY] = 'X';
    if (solveMaze(maze, startX + 1, startY, targetX, targetY) ||
        solveMaze(maze, startX, startY + 1, targetX, targetY) ||
        solveMaze(maze, startX - 1, startY, targetX, targetY) ||
        solveMaze(maze, startX, startY - 1, targetX, targetY)) {
      return true;
    }
    return false;
}

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

public static boolean solveMaze(char[][] maze, 
                                int startX, int startY, int targetX, int targetY) {

    if (startX < 0 || startX >= maze.length ||
        startY < 0 || startY >= maze[0].length ||
        maze[startX][startY] == 'X') {
      return false;
    }
    if (startX == targetX && startY == targetY) {
      return true;
    }
    maze[startX][startY] = 'X';
    int[] dx = {1, 0, -1, 0};
    int[] dy = {0, 1, 0, -1};
    for (int i = 0; i < 4; i++) {
      if (solveMaze(maze, startX + dx[i], startY + dy[i], targetX, targetY)) {
        return true;
      }
    }
    return false;
}

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

public static boolean solveMaze(char[][] maze, 
                                int startX, int startY, int targetX, int targetY) {

    if (startX == targetX && startY == targetY) {
      return true;
    }
    maze[startX][startY] = 'X';
    int[] dx = {1, 0, -1, 0};
    int[] dy = {0, 1, 0, -1};
    for (int i = 0; i < 4; i++) {
      int newX = startX + dx[i], newY = startY + dy[i];
      if (newX < 0 || newX >= maze.length || newY < 0 || newY >= maze.length ||
          maze[newX][newY] == 'X') {
        continue;
      }
      if (solveMaze(maze, newX, newY, targetX, targetY)) {
        return true;
      }
    }
    return false;
}

迷宫

给定一个迷宫，一个起点和一个目标点，返回是否可以到达目标点。

public static boolean solveMaze(char[][] maze, 
                                int startX, int startY, int targetX, int targetY,
                                String path) {
    if (startX < 0 || startX >= maze.length ||
        startY < 0 || startY >= maze[0].length ||
        maze[startX][startY] == 'X') {
      return false;
    }
    if (startX == targetX && startY == targetY) {
      System.out.println(path);
      return true;
    }
    maze[startX][startY] = 'X';
    int[] dx = {1, 0, -1, 0};
    int[] dy = {0, 1, 0, -1};
    char[] direction = {'D', 'R', 'U', 'L'};
    for (int i = 0; i < 4; i++) {
      String newPath = path + direction[i] + " ";
      if (solveMaze(maze, startX+dx[i], startY+dy[i], targetX, targetY, newPath)) {
        return true;
      }
    }
    return false;
}

迷宫

给定一个迷宫，一个起点和一个目标点，输出到达目标点的路径。

public static boolean solveMaze(char[][] maze, 
                                int startX, int startY, int targetX, int targetY,
                                ArrayList<Character> path) {
    if (startX < 0 || startX >= maze.length ||
        startY < 0 || startY >= maze[0].length ||
        maze[startX][startY] == 'X') {
      return false;
    }
    if (startX == targetX && startY == targetY) {
      return true;
    }
    maze[startX][startY] = 'X';
    int[] dx = {1, 0, -1, 0};
    int[] dy = {0, 1, 0, -1};
    char[] direction = {'D', 'R', 'U', 'L'};
    for (int i = 0; i < 4; i++) {
      path.add(direction[i]);
      if (solveMaze(maze, startX+dx[i], startY+dy[i], targetX, targetY, path)) {
        return true;
      }
      path.remove(path.size()-1);
    }
    return false;
}

迷宫

给定一个迷宫，一个起点和一个目标点，返回到达目标点的路径。

回溯算法总结

回溯算法的含义是尝试、迭代、遍历等
不断地在搜索空间中尝试，直到
- 找到解决方案
- 无法尝试更多的方法
一个Level-N 问题 -> M * Level-(N-1) 个子问题
- 当进入子问题时，对于共享字段应该保持状态不变

背包问题

给定一组候选数字（C）和一个目标数字（T），找出C中所有唯一组合，使得候选数字的总和等于T。

所有候选数字都是唯一的。

可以从C中选择相同重复的数字，数量不限。

注意：

所有数字（包括目标数字）将是正整数。
组合中的元素（a1，a2，…，ak）必须按非降序排列。（即，a1 ≤ a2 ≤ …≤ ak）。
解决方案集不能包含重复的组合。

示例输入: [7], [2, 3, 6, 7]

示例输出: [[2, 2, 3], [7]]

背包问题

将问题定义为 (C, i, T)，然后给定一个数字

选择 => (C, i, T-C[i])
不选择 => (C, i+1, T)

给定一组候选数字（C）和一个目标数字（T），找出C中所有唯一组合，使得候选数字的总和等于T。

所有候选数字都是唯一的。

可以从C中选择相同重复的数字，数量不限。

背包问题

public static ArrayList<ArrayList<Integer>> knapsack(int[] candidates, 
                                                     int target) {
    ArrayList<ArrayList<Integer>> results = new ArrayList<ArrayList<Integer>>();
    ArrayList<Integer> cur = new ArrayList<Integer>();
    knapsack(candidates, 0, target, results, cur);
    return results;
}
public static void knapsack(int[] candidates, int index, int target,
                            ArrayList<ArrayList<Integer>> results,
                            ArrayList<Integer> cur) {
    if (target < 0 || (target != 0 && index == candidates.length)) {
        return;
    }
    if (target == 0) {
        results.add(new ArrayList<Integer>(cur));
        return;
    }
    cur.add(candidates[index]);
    knapsack(candidates, index, target-candidates[index], results, cur);
    cur.remove(cur.size()-1);
    knapsack(candidates, index+1, target, results, cur);
}

给定一组候选数字（C）和一个目标数字（T），找出C中所有唯一组合，使得候选数字的总和等于T。

背包问题

给定一组候选数字（C）和一个目标数字（T），找出C中所有唯一组合，使得候选数字的总和等于T。

所有候选数字都是唯一的。

可以从C中选择相同重复的数字，数量不限。

迭代所有数字来决定是否选择当前数字。

<=>

在当前集合中，应该选择哪一个数字作为最小值。

背包问题

Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.

public ArrayList<ArrayList<Integer>> knapsack(int[] candidates, int target) {
    ArrayList<ArrayList<Integer>> results = new ArrayList<ArrayList<Integer>>();
    ArrayList<Integer> cur = new ArrayList<Integer>();
    knapsack(candidates, 0, target, results, cur);
    return results;
}
public void knapsack(int[] candidates, int index, int target,
                     ArrayList<ArrayList<Integer>> results,
                     ArrayList<Integer> cur) {
    if (target < 0) {
        return;
    }
    if (target == 0) {
        results.add(new ArrayList<Integer>(cur));
        return;
    }
    for (int i = index; i < candidates.length; i++) {
        cur.add(candidates[i]);
        knapsack(candidates, i, target-candidates[i], results, cur);
        cur.remove(cur.size()-1);
    }
    return;
}

背包问题 II

给定一组候选数字（C）和一个目标数字（T），找出C中所有唯一组合，使得候选数字的总和等于T。

候选数字可能包含重复项。

每个C中的数字在组合中只能使用一次。

public List<List<Integer>> knapsack(int[] candidates, int target) {
    Arrays.sort(candidates);
    List<List<Integer>> results = new ArrayList<List<Integer>>();
    List<Integer> cur = new ArrayList<Integer>();
    knapsack(candidates, 0, target, results, cur);
    return results;
}

public void knapsack(int[] candidates, int index, int target,
                     List<List<Integer>> results, List<Integer> cur) {
    if (target < 0)  return;
    if (target == 0) {
        results.add(new ArrayList<Integer>(cur));
        return;
    }
    for (int i = index; i < candidates.length; i++) {
        cur.add(candidates[i]);
        knapsack(candidates, i+1, target-candidates[i], results, cur);
        cur.remove(cur.size()-1);
        while (i < candidates.length-1 && candidates[i] == candidates[i+1]) i++;
    }
    return;
}

0-1 背包问题 II

给定一个可容纳重量为s磅的背包，还有一组物品，它们的重量分别为w1、w2、...wn。尝试尽可能多地将物品放入背包中，返回我们可以在背包中获得的最大重量。

public int knapsack(int s, int[] weights) {
    return knapsack(s, weights, 0);
}

public int knapsack(int s, int[] weights, int index) {
    if (s == 0 || index == weights.length) {
      return 0;
    }
    if (weights[index] > s) {
      return knapsack(s, weights, index+1);
    }
    return Math.max(knapsack(s, weights, index+1),
                    weights[index] + knapsack(s-weights[index], weights, index+1));
}

这不是最优解，我们可以使用动态规划算法来解决

排列 (Leetcode 46)

给定一个不重复的数字集合，返回所有可能的排列。

例如，
[1,2,3] 有以下排列：
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], 和 [3,2,1].

public List<List<Integer>> permute(int[] nums) {
// Implement this method.
}

给定一个不重复的数字集合，返回所有可能的排列。

public List<List<Integer>> permute(int[] num) {
    List<List<Integer>> results = new ArrayList<List<Integer>>();
    permute(results, new ArrayList<Integer>(), num);
    return results;
}
    
public void permute(List<List<Integer>> results,
                    ArrayList<Integer> cur, int[] num) {
    if (cur.size() == num.length) {
        results.add(new ArrayList<Integer>(cur));
        return;
    }
    for (int i = 0; i < num.length; i++) {
        if (cur.contains(num[i])) {
            continue;
        }
        cur.add(num[i]);
        permute(results, cur, num);
        cur.remove(cur.size() - 1);
    }
}

排列 (Leetcode 46)

给定一个不重复的数字集合，返回所有可能的排列。

public ArrayList<ArrayList<Integer>> permute(int[] num) {
    ArrayList<Integer> numList = new ArrayList<Integer>();
    for (int i = 0; i < num.length; i++)
        numList.add(num[i]);
    return permute(new ArrayList<Integer>(), numList);
}

public ArrayList<ArrayList<Integer>> permute(ArrayList<Integer> cur,
                                             ArrayList<Integer> num) {
    ArrayList<ArrayList<Integer>> results =
         new ArrayList<ArrayList<Integer>>();
    if (num.size() == 0) {
        results.add(cur);
        return results;
    }
    for (int i = 0; i < num.size(); i++) {
        ArrayList<Integer> newCur = new ArrayList<Integer>(cur);
        newCur.add(num.get(i));
        ArrayList<Integer> newNum = new ArrayList<Integer>(num);
        newNum.remove(i);
        results.addAll(permute(newCur, newNum));
    }
    return results;
}

排列 (Leetcode 46)

给定一个不重复的数字集合，返回所有可能的排列。

public List<List<Integer>> permute(int[] num) {
    return permute(new ArrayList<Integer>(), num);
}

public List<List<Integer>> permute(ArrayList<Integer> cur, int[] num) {
    List<List<Integer>> results = new ArrayList<List<Integer>>();
    if (cur.size() == num.length) {
        results.add(new ArrayList<Integer>(cur));
        return results;
    }
    for (int i = 0; i < num.length; i++) {
        if (cur.contains(num[i])) {
            continue;
        }
        cur.add(num[i]);
        results.addAll(permute(cur, num));
        cur.remove(cur.size() - 1);
    }
    return results;
}

排列 (Leetcode 46)

给定一个不重复的数字集合，返回所有可能的排列。

以上的解决方案都有一些缺点

交换方法

1 2 3 4 5

2 1 3 4 5

3 2 1 4 5

4 2 3 1 5

5 2 3 4 1

{

2 1 3 4 5

2 3 1 4 5

2 4 3 1 5

2 5 3 4 1

排列(Leetcode 46)

给定一个不重复的数字集合，返回所有可能的排列。

public List<List<Integer>> permute(int[] num) {
    List<List<Integer>> results = new ArrayList<List<Integer>>();
    permute(results, num, 0);
    return results;
}

public void permute(List<List<Integer>> results, int[] num, int index) {
    if (index == num.length) {
	ArrayList<Integer> result = new ArrayList<>();
	for (int i = 0; i < num.length; i++) {
	    result.add(num[i]);
	}
	results.add(result);
	return;
    }
    for (int i = index; i < num.length; i++) {
	swap(num, index, i);
	permute(results, num, index + 1);
	swap(num, index, i);
    }
}
public void swap(int[] num, int i, int j) {
    int temp = num[i];
    num[i] = num[j];
    num[j] = temp;
}

排列 II (Leetcode 47)

给定一个~~不重复的~~数字集合，返回所有可能的排列。

public List<List<Integer>> permuteUnique(int[] num) {
    List<List<Integer>> results = new ArrayList<List<Integer>>();
    List<Integer> numList = new ArrayList<>();
    Arrays.sort(num);
    for (int i = 0; i < num.length; i++)
        numList.add(num[i]);
    permute(results, new ArrayList<Integer>(), numList);
    return results;
}

public void permute(List<List<Integer>> results,
    List<Integer> cur, List<Integer> num) {
    if (num.size() == 0) {
        results.add(cur);
        return;
    }
    for (int i = 0; i < num.size(); i++) {
        if (i > 0 && num.get(i) == num.get(i-1))
            continue;
        ArrayList<Integer> newCur = new ArrayList<>(cur);
        newCur.add(num.get(i));
        ArrayList<Integer> newNum = new ArrayList<>(num);
        newNum.remove(i);
        permute(results, newCur, newNum);
    }
    return;
}

在生成排列之前减少重复项

排列 II (Leetcode 47)

给定一个~~不重复的~~数字集合，返回所有可能的排列。

public List<List<Integer>> permuteUnique(int[] num) {
    List<List<Integer>> results = new ArrayList<List<Integer>>();
    Arrays.sort(num);
    boolean[] visited = new boolean[num.length];
    for (int i = 0; i < visited.length; i++) {
        visited[i] = false;
    }
    permute(results, new ArrayList<Integer>(), num, visited);
    return results;
}

public void permute(List<List<Integer>> results, List<Integer> cur, int[] num, boolean[] visited) {
    if (cur.size() == num.length) {
        results.add(new ArrayList<Integer>(cur));
        return;
    }
    for (int i = 0; i < num.length; i++) {
        if (visited[i] || (i > 0 && num[i] == num[i-1] && !visited[i-1])) {
            continue;
        }
        visited[i] = true;
        cur.add(num[i]);
        permute(results, cur, num, visited);
        cur.remove(cur.size() - 1);
        visited[i] = false;
    }
    return;
}

组合

给定一组不同的数字，返回所有可能的组合。

例如,
[2, 6, 8] 有以下幂集（组合）：
[], [2], [6], [8], [2, 6], [2, 8], [6, 8], [2, 6, 8].

public List<List<Integer>> combine(int[] nums) {
// Implement this method.
}

组合

给定一组不同的数字，返回所有可能的组合。

public static List<List<Integer>> combine(int[] nums) {
    List<List<Integer>> results = new ArrayList<>();
    combination(results, nums, 0, new ArrayList<Integer>());
    return results;
}

public static void combination(List<List<Integer>> results, 
                               int[] nums, int index, ArrayList<Integer> items) {
    if (index == nums.length) {
      results.add(items);
      return;
    }
    ArrayList<Integer> newItems1 = new ArrayList<Integer>(items);
    combination(results, nums, index+1, newItems1);
    
    ArrayList<Integer> newItems2 = new ArrayList<Integer>(items);
    newItems2.add(nums[index]);
    combination(results, nums, index+1, newItems2);
  }

组合

给定一组不同的数字，返回所有可能的组合。

public static List<List<Integer>> combine(int[] nums) {
    List<List<Integer>> results = new ArrayList<>();
    combination(results, nums, 0, new ArrayList<Integer>());
    return results;
}

public static void combination(List<List<Integer>> results, 
                               int[] nums, int index, ArrayList<Integer> items) {
    if (index == nums.length) {
      results.add(new ArrayList<Integer>(items));
      return;
    }
    combination(results, nums, index+1, items);
    
    items.add(nums[index]);
    combination(results, nums, index+1, items);
    items.remove(items.size()-1);
  }

组合

给定一组不同的数字，返回所有可能的组合。

public static List<List<Integer>> combine(int[] nums) {
    List<List<Integer>> results = new ArrayList<>();
    combination(results, nums, 0, new ArrayList<Integer>());
    return results;
}

public static void combination(List<List<Integer>> results, 
                               int[] nums, int index,
                               ArrayList<Integer> items) {
    if (index == nums.length) {
      results.add(new ArrayList<Integer>(items));
      return;
    }
    for (int i = index; i < nums.length; i++) {
      items.add(nums[i]);
      combination(results, nums, i+1, items);
      items.remove(items.size()-1);
    }
}

The empty set is missing.

-There will be at least one element in the "items"

input: 2 6 8

output:

2,8

6,8

2,6,8

组合

给定一组不同的数字，返回所有可能的组合。

public static List<List<Integer>> combine(int[] nums) {
    List<List<Integer>> results = new ArrayList<>();
    combination(results, nums, 0, new ArrayList<Integer>());
    return results;
}

public static void combination(List<List<Integer>> results, 
                               int[] nums, int index,
                               ArrayList<Integer> items) {
    if (index == nums.length) {
      results.add(new ArrayList<Integer>(items));
      return;
    }
    for (int i = index; i <= nums.length; i++) {
      if (i == nums.length) {
        combination(results, nums, i, items);
        return;
      }
      items.add(nums[i]);
      combination(results, nums, i+1, items);
      items.remove(items.size()-1);
    }
}

添加了一个空集合

组合

给定一组不同的数字，返回所有可能的组合。

public static List<List<Integer>> combine(int[] nums) {
    List<List<Integer>> results = new ArrayList<>();
    combination(results, nums, 0, new ArrayList<Integer>());
    return results;
}

public static void combination(List<List<Integer>> results, 
                               int[] nums, int index,
                               ArrayList<Integer> items) {
    if (index == nums.length) {
      results.add(new ArrayList<Integer>(items));
      return;
    }
    for (int i = index; i < nums.length; i++) {
      items.add(nums[i]);
      combination(results, nums, i+1, items);
      items.remove(items.size()-1);
    }
    combination(results, nums, nums.length, items);
}

和上面的一样

幸运数字

888是一个幸运数字。对于每个美国电话号码，我们实际上可以添加一些运算符使其变成888。例如：

电话号码为7765332111，则可以得到：

7/7*65*3+3*21*11 = 888

776+5+3*32+11*1 = 888

...

我们希望得到所有可以得到特定幸运数字的运算方程列表。接口将为

List<String> luckyNumbers(String num, int target)

幸运数字

我们希望得到所有可以得到特定幸运数字的运算方程列表。接口将为

List<String> luckyNumbers(String num, int target)

附加信息：

由于是电话号码，字符串num将始终为10个数字。

我们可以有“0”，但不能有“05”，“032”。

如果一个数字不能被分割，就不能使用它。例如，55/2是不允许的，您需要确保除法始终是整数结果。

0不能被分割。

幸运数字

我们需要使用递归来解决这个问题。

由于我们要输出结果，有一些需要注意的事项：

第一个数字前面没有运算符。
为了避免数字溢出，需要使用long类型。
*和/的优先级高于+和-。如何处理这一点？
需要注意0的情况。

幸运数字

public List<String> luckyNumbers(String num, int target) {
    List<String> result = new ArrayList<>();
    recursion(num, target, "", 0, 0, 0, result);
    return result;
}
public void recursion(String num, int target, String temp, int pos, 
                        long current, long last, List<String> result) {
    if (pos == num.length()) {
        if (current == target) {
            result.add(temp);
        }
        return;
    }
    for (int i = pos; i < num.length(); i ++) {
        if (num.charAt(pos) == '0' && i != pos) break;
        String m = num.substring(pos, i + 1);
        long n = Long.valueOf(m);
        if (pos == 0) {
            recursion(num, target, temp + m, i + 1, n, n, result);
        } else {
            recursion(num, target, temp + "+" + m, i + 1, current + n, n, result);
            recursion(num, target, temp + "-" + m, i + 1, current - n, -n, result);
            recursion(num, target, temp + "*" + m, i + 1, current - last + last * n, last * n, result);
            if (n != 0 && last % n == 0) {
                recursion(num, target, temp + "/" + m, i + 1, current - last + last / n, last / n, result);
            }
        }
    }
}