树




定义
树是一种(可能非线性的)数据结构,由节点或顶点和边组成,不具有任何循环。



树
树是算法中最重要的数据结构之一
像我们目前的文件系统
树有许多不同的类型



树
Tree
B Tree
Trie Tree
Binary Tree
BST
RB Tree
AVL



术语
- 节点
- 根节点
- 叶子节点
- 父节点
- 子节点
- 兄弟节点
- 祖先节点
- 后代节点
- 边
- 高度
- 深度
- 层级
- 路径
A
B
C
D
E
F
G
J
I
H



二叉树
- 它实际上与树结构不同
- 它有右子树和左子树
- 每个节点最多只能有两个孩子



完全二叉树
- 完全二叉树在算法问题中非常有用
- 通常我们会把树的属性作为计算时间复杂度的前提条件
- 路径之和是最小的



二叉树的属性
- 在第 i 层上,最多有 2^i 个节点
- 高度为k的树,最多有2^k-1个节点。
- 一个有n个节点的完整二叉树,高度将是
- 如果我们从根节点开始编号,并基于每个层级进行编号,对于完全二叉树,我们将有:
- 对于节点编号为 k,其左子节点的编号是 2k+1。
- 对于节点编号为k,它的右子节点为2k+2。
- 如何存储二叉树?完全二叉树呢?



二叉树的基本数据结构
public class BinaryTree<T> {
private Node<T> root;
public Tree(T rootData) {
root = new Node<T>();
root.data = rootData;
}
public static class Node<T> {
private T data;
private Node<T> leftNode;
private Node<T> rightNode;
}
}


二叉树的遍历
- 前序遍历:父节点,左子节点,右子节点
- 中序遍历:左子节点,父节点,右子节点
- 后序遍历:左子节点,右子节点,父节点



二叉树的遍历
A
B
D
E
H
I
J
G
F
C
先历顺序: A B D E H I C F G J
中序遍历: D B H E I A F C G J
后序遍历: D H I E B F J G C A



二叉树的遍历
我们需要使用递归来遍历一棵树
public void preorder(TreeNode root) {
if(root != null) {
//Visit the node by Printing the node data
System.out.printf("%c ",root.data);
preorder(root.left);
preorder(root.right);
}
} 


Traversal of a Binary Tree
public void inorder(TreeNode root) {
if(root != null) {
inorder(root.left);
System.out.printf("%c ",root.data);
inorder(root.right);
}
} public void postorder(TreeNode root) {
if(root != null) {
postorder(root.left);
postorder(root.right);
System.out.printf("%c ",root.data);
}
} 


二叉树的遍历
我们能否使用栈来遍历树而不使用递归?



二叉树的遍历
前序遍历:访问当前节点,将右子节点压入栈中,再将左子节点压入栈中
因为需要先访问左子节点



二叉树的遍历
public static void PreOrder(Node root) {
Stack<Node> nodeStack = new Stack<Node>();
nodeStack.push(root);
while(!nodeStack.empty()) {
Node node = nodeStack.pop();
System.out.printf("%c ", node.data);
if(node.rightNode != null) {
nodeStack.push(node.rightNode);
}
if(node.leftNode != null) {
nodeStack.push(node.leftNode);
}
}
}


二叉树的遍历
我们有更好的方法吗?
我们能否在堆栈上节省一些空间?
我们需要同时将两个子节点推入栈中吗?



二叉树的遍历
public static void PreOrder2(Node root) {
Stack<Node> nodeStack = new Stack<Node>();
nodeStack.push(root);
Node node = root;
while(!nodeStack.empty()) {
System.out.printf("%c ", node.data);
if(node.rightNode != null) {
nodeStack.push(node.rightNode);
}
if(node.leftNode != null) {
node = node.leftNode;
}
else {
node = nodeStack.pop();
}
}
}


二叉树的遍历
中序遍历:我们应该怎么做?
中序遍历: 我们将当前节点压入栈中,然后一直向左走,如果没有左节点了,就弹出当前节点,输出它的值,并将指针指向右节点



二叉树的遍历
public static void InOrder(Node root) {
Stack<Node> nodeStack = new Stack<Node>();
Node node = root;
while(!nodeStack.empty() || node != null) {
if(node != null) {
nodeStack.push(node);
node = node.leftNode;
}
else {
node = nodeStack.pop();
System.out.printf("%c ", node.data);
node = node.rightNode;
}
}
}


二叉树的遍历
后序遍历是最困难的一种遍历方式
后序遍历:先往左走,如果没有左孩子,则访问它。然后对于栈顶的节点,我们现在访问它吗?
不,因为那是中序遍历
我们需要接着往右边走,直到不能再走,然后访问并弹出



二叉树的遍历
二叉树的后序遍历是最难的一种遍历方式
可以通过对当前数据结构的操作来实现后序遍历吗?
不行。我们不知道栈顶元素的状态。右子树是否已经被遍历过了呢?



二叉树的遍历
我们需要一个额外的标志来存储节点的状态
static class NodeWithFlag {
Node node;
boolean flag;
public NodeWithFlag(Node n, boolean value) {
node = n;
flag = value;
}
}在我们访问完右子节点后,我们会更新标志;



二叉树的遍历
public static void PostOrder(Node root) {
Stack<NodeWithFlag> nodeStack = new Stack<NodeWithFlag>();
Node curNode = root;
NodeWithFlag newNode;
while(!nodeStack.empty() || curNode != null) {
while(curNode != null) {
newNode = new NodeWithFlag(curNode, false);
nodeStack.push(newNode);
curNode = curNode.leftNode;
}
newNode = nodeStack.pop();
curNode = newNode.node;
if(!newNode.flag) {
newNode.flag = true;
nodeStack.push(newNode);
curNode = curNode.rightNode;
}
else {
System.out.printf("%c ", curNode.data);
curNode = null;
}
}
}


二叉树的遍历
另一种方法是使用 HashSet 存储已访问的节点



第一次访问:HashSet.contains() == false -> 加入到集合中
第二次访问:HashSet.contains() == true -> 输出该节点的值
构建一棵二叉树
如果我们有一个树的遍历结果,我们能构造出这个树吗?
前序遍历: A B C D
A
B
D
C
A
B
D
C



构造二叉树
无论是给定先序遍历、中序遍历还是后序遍历,都可以构建不同的二叉树
如果我们给出两个遍历结果呢?



构造二叉树
先序遍历(PreOrder): A B C D
A
B
D
C
A
B
D
C
中序遍历(InOrder): B A D C



构造二叉树
先序遍历(PreOrder): A B C D
A
B
D
C
后序遍历(PostOrder): B D C A
A
B
D
C



构造二叉树
结论:你需要两次遍历才能构造一棵树,其中之一必须是中序遍历
请给出一个先序遍历和中序遍历,如何构建一棵二叉树?



构造二叉树
A
B
D
E
H
I
J
G
F
C
先序遍历(PreOrder): A B D E H I C F G J
中序遍历(InOrder): D B H E I A F C G J
A是根节点,所以A是先序遍历中的第一个节点,而中序遍历可以使用A来分离左子树和右子树
然后我们可以进行递归



先序+中序
public TreeNode buildTree(int[] preorder, int[] inorder) {
int preStart = 0;
int preEnd = preorder.length-1;
int inStart = 0;
int inEnd = inorder.length-1;
return construct(preorder, preStart, preEnd, inorder, inStart, inEnd);
}
public TreeNode construct(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd){
if(preStart>preEnd||inStart>inEnd){
return null;
}
int val = preorder[preStart];
TreeNode p = new TreeNode(val);
int k=0;
for(int i=inStart; i<=inEnd; i++){
if(val == inorder[i]){
k=i;
break;
}
}
p.left = construct(preorder, preStart+1, preStart+(k-inStart), inorder, inStart, k-1);
p.right= construct(preorder, preStart+(k-inStart)+1, preEnd, inorder, k+1 , inEnd);
return p;
}


构建一棵二叉树
A
B
D
E
H
I
J
G
F
C
后序遍历(PostOrder): D H I E B F J G C A
中序遍历(InOrder): D B H E I A F C G J
这种构建二叉树的方法和先序遍历+中序遍历的方法类似,唯一的不同在于根节点现在是后序遍历中的最后一个元素



后序+中序
public TreeNode buildTree(int[] inorder, int[] postorder) {
int inStart = 0;
int inEnd = inorder.length - 1;
int postStart = 0;
int postEnd = postorder.length - 1;
return build(inorder, inStart, inEnd, postorder, postStart, postEnd);
}
public TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {
if (inStart > inEnd || postStart > postEnd)
return null;
int rootValue = postorder[postEnd];
TreeNode root = new TreeNode(rootValue);
int k = 0;
for (int i = inStart; i <=inEnd; i++) {
if (inorder[i] == rootValue) {
k = i;
break;
}
}
root.left = build(inorder, inStart, k - 1, postorder, postStart,
postStart + k - (inStart + 1));
root.right = build(inorder, k + 1, inEnd, postorder, postStart + k- inStart, postEnd - 1);
return root;
}


二叉搜索树
30
18
13
24
22
27
47
40
31
34



二叉搜索树
- 所有子树都是BST
- 所有左子树的元素都小于根节点
- 所有右子树中的元素都比根节点大
- 如果我们进行中序遍历,二叉搜索树的结果将是一个排序后的数组



二叉搜索树
- 查找
- 添加
-
删除



二叉搜索树
30
18
13
24
22
27
47
40
31
34
查找 24
- 30 > 24 -> 走左边
- 18 < 24 -> 走右边
- 找到 24,返回 true
查找42
- 30 < 42 -> 往右子树走
- 34 < 42 -> 往右子树走
- 40 < 42 -> 往右子树走
- 47 > 42 -> 往左子树走
- 左子树没有,返回false



二叉搜索树
public static boolean find(int value, Node root) {
Node node = root;
while(node != null) {
if(node.data > value) {
node = node.leftNode;
}
else if(node.data < value) {
node = node.rightNode;
}
else return true;
}
return false;
}


二叉搜索树
30
18
13
24
22
27
47
40
31
34
添加 42
- 首先需要确定树中是否已经存在值为42的节点
- 找到我们放置42的位置



二叉搜索树
30
18
13
24
22
27
47
40
31
34
30
18
13
24
22
27
47
40
31
34
42



二叉搜索树
public static boolean add(int value, Node root) {
if(root == null) {
root = new Node(value);
return true;
}
Node node = root;
while(node != null) {
if(node.data > value) {
if(node.leftNode != null) {
node = node.leftNode;
}
else {
node.leftNode = new Node(value);
return true;
}
}
else if(node.data < value) {
if(node.rightNode != null) {
node = node.rightNode;
}
else {
node.rightNode = new Node(value);
return true;
}
}
else return false;
}
return false;
}


二叉搜索树
查找和添加元素到树中的时间复杂度是多少?



二叉搜索树
30
18
13
24
22
27
47
40
31
34
移除 27
- 首先我们需要确认树中是否存在27
- 然后我们需要移除27
移除30
- 我们如何去除不是叶子的东西?



二叉搜索树
- 如果 Q 是叶子节点
- 如果 Q 只有一个孩子
- 如果孩子 R 是右孩子
- 如果孩子 R 是左孩子
- 如果 Q 有两个孩子



二叉搜索树
P
Q
R
P
Q
R
P
Q
R
P
Q
R
P<R<Q
P<Q<R
R<Q<P
Q<R<P
只要用R来代替Q



二叉搜索树
P
Q
R1
R2
如果我们移除 Q,哪个元素最适合替代它呢?






二叉搜索树
P
Q
R1
R2
考虑中序遍历,在Q之前和之后的节点是最佳替代者,因为如果它们替代Q,再进行中序遍历,输出结果仍然是一个排序的数组,这意味着树仍然是BST。
那么,这两个节点在哪里?



二叉搜索树
P
Q
R1
R2
因此,位于 Q 前面的元素是子树 R1 中的最大节点,而位于 Q 后面的元素是子树 R2 中的最小节点。
这个节点有没有子节点?我们能直接移除它们吗?
也许有,但最多只有一个,所以我们回到条件2。



public static boolean remove(int value, Node root) {
if(root == null) return false;
if(root.data == value) {
root = removeNode(root);
return true;
}
Node node = root;
while(node != null) {
if(node.data > value) {
if(node.leftNode != null && node.leftNode.data != value) {
node = node.leftNode;
}
else if(node.leftNode == null) return false;
else {
node.leftNode = removeNode(node.leftNode);
return true;
}
}
else if(node.data < value) {
if(node.rightNode != null && node.rightNode.data != value) {
node = node.rightNode;
}
else if(node.rightNode == null) return false;
else {
node.rightNode = removeNode(node.rightNode);
return true;
}
}
else return false;
}
return false;
}


二叉搜索树(续)
public static Node removeNode(Node node) {
if(node.leftNode == null && node.rightNode == null) {
return null;
}
else if(node.leftNode == null) {
return node.rightNode;
}
else if(node.rightNode == null) {
return node.leftNode;
}
else {
node.data = findAndRemove(node);
return node;
}
}
public static int findAndRemove(Node node) {
int result;
if(node.leftNode.rightNode == null) {
result = node.leftNode.data;
node.leftNode = node.leftNode.leftNode;
return result;
}
node = node.leftNode;
while(node.rightNode.rightNode != null) {
node = node.rightNode;
}
result = node.rightNode.data;
node.rightNode = node.rightNode.leftNode;
return result;
}


二叉搜索树
30
18
13
24
22
27
47
40
31
34
42
43
30
18
13
24
22
27
47
43
34
40
42
31



二叉搜索树
我们知道搜索时间与树的高度密切相关。
如果我们不断添加和删除元素,树就会变得不平衡。
因此,我们有红黑树和AVL树,它们可以使用旋转和重构来使树保持平衡。



Trie Tree(字典树)



字典树
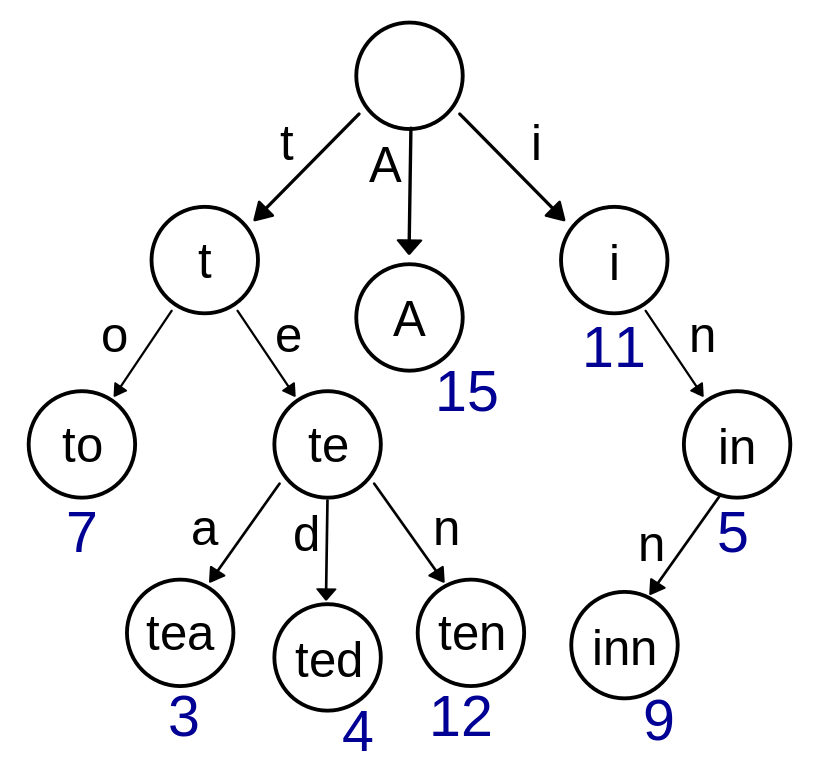



字典树
在计算机科学中,Trie树也被称为数字树,有时也称为基数树或前缀树(因为可以按前缀搜索),它是一种用于存储动态集合或关联数组的有序树数据结构,其中键通常是字符串。



What Trie Tree Can Help?
- 它可以很好地存储字典,而且不会占用太多额外的空间。
- 它可以轻松地找到两个字符串的公共前缀(这在输入提示中非常有用)。
- 它可以轻松地查找单词是否在字典中(维护顺序)。



复杂度分析
在插入和查找中,需要注意的是,在树中下降一个级别可以在常数时间内完成,每次程序下降一个级别,一个字符就会从字符串中删除。
我们可以得出结论,每个函数将在树中下降L级,每次函数在树中下降一级,时间复杂度为常数,因此在Trie中插入和查找单词的时间复杂度为O(L)。
Trie树所使用的内存取决于存储边缘的方法以及有多少个单词具有相同的前缀。



实现 Trie (前缀树)
实现一个 trie,包含插入 (insert),查找 (search),以及按前缀查找 (startsWith) 方法。
我们只使用小写字母'a'到'z'
一个节点有多少个子节点?



实现 Trie (前缀树)
class TrieNode {
// Initialize your data structure here.
boolean isWord;
TrieNode[] children;
public TrieNode() {
children = new TrieNode[26];
isWord = false;
}
}


实现 Trie (前缀树)
public class Trie {
private TrieNode root;
public Trie() {
root = new TrieNode();
}
// Inserts a word into the trie.
public void insert(String word) {
if(word == null || word.length() == 0) return;
TrieNode pNode = root;
for(int i = 0; i < word.length(); i ++) {
char c = word.charAt(i);
int index = c - 'a';
if(pNode.children[index] == null) {
TrieNode newNode = new TrieNode();
pNode.children[index] = newNode;
}
pNode = pNode.children[index];
}
pNode.isWord = true;
}
}


实现 Trie (前缀树)
// Returns if the word is in the trie.
public boolean search(String word) {
TrieNode pNode = root;
if(word == null || word.length() == 0) return true;
for(int i = 0; i < word.length(); i ++) {
int index = word.charAt(i) - 'a';
pNode = pNode.children[index];
if(pNode == null) return false;
}
return pNode.isWord;
}
// Returns if there is any word in the trie that starts with the given prefix.
public boolean startsWith(String prefix) {
TrieNode pNode = root;
if(prefix == null || prefix.length() == 0) return true;
for(int i = 0; i < prefix.length(); i ++) {
int index = prefix.charAt(i) - 'a';
pNode = pNode.children[index];
if(pNode == null) return false;
}
return true;
}


设计内存文件系统
设计一个内存文件系统,模拟以下功能:
ls:给定一个字符串格式的路径。如果它是一个文件路径,则返回只包含该文件名的列表。如果它是一个目录路径,则返回该目录中文件和目录名称的列表。输出(文件和目录名称一起)应按字典顺序排列。
mkdir:给定一个不存在的目录路径,应根据路径创建一个新的目录。如果路径中间的目录也不存在,则需要创建它们。此函数返回void类型。
addContentToFile:给定一个文件路径和字符串格式的文件内容。如果文件不存在,则需要创建包含给定内容的文件。如果文件已经存在,则需要将给定内容追加到原始内容。此函数返回void类型。
readContentFromFile:给定一个文件路径,返回其字符串格式的内容。



设计内存文件系统



我们提到文件系统是一棵树。
文件系统可以在每个节点下拥有很多子节点。因此,使用 Trie 来表示它是一个不错的选择。
class TrieNode {
// Initialize your data structure here.
boolean isFile;
String content;
Map<String, TrieNode> children;
public TrieNode() {
isFile = false;
children = new HashMap<>();
}
}设计内存文件系统



class FileSystem {
TrieNode root;
public FileSystem() {
root = new TrieNode();
}
public List<String> ls(String path) {
List<String> results = new ArrayList<>();
TrieNode cur = root;
String[] routes = path.split("/");
for (int i = 1; i < routes.length; i ++) {
cur = cur.children.get(routes[i]);
}
if (cur.isFile) {
results.add(routes[routes.length - 1]);
} else {
results.addAll(cur.children.keySet());
Collections.sort(results);
}
return results;
}
public void mkdir(String path) {
getCurrentNode(path);
}
}Design In-Memory File System



class FileSystem {
TrieNode root;
public FileSystem() {
root = new TrieNode();
}
public void addContentToFile(String filePath, String content) {
TrieNode cur = getCurrentNode(filePath);
cur.isFile = true;
if (cur.content == null) {
cur.content = new String(content);
} else {
cur.content = cur.content.concat(content);
}
}
public String readContentFromFile(String filePath) {
TrieNode cur = getCurrentNode(filePath);
return cur.content;
}
private TrieNode getCurrentNode(String path) {
TrieNode cur = root;
String[] routes = path.split("/");
for (int i = 1; i < routes.length; i ++) {
if (!cur.children.containsKey(routes[i])) {
cur.children.put(routes[i], new TrieNode());
}
cur = cur.children.get(routes[i]);
}
return cur;
}
}其他类型的Trie
我们使用 Trie 来存储只含有小写字母的单词,但是 Trie 也可以用来存储许多其他的数据。我们可以使用位或字节代替小写字母,而且 Trie 还能够存储各种数据类型,而不仅仅是字符串。



作业


