Recursion

What is recursion

Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem (as opposed to iteration).

How to solve a problem

Divide into small problems.
Solve small problems.
Use the result of small problems to solve the original problem.
If the small problems are the same as original one, just scale is different. Then this is called recursion.

Recursion Properties

Base case
- simple scenario that does not need recursion to produce an answer.
Recursion
- a set of rules that reduce all other case toward the base case.

Code problem with recursion

Base case
recursion rules
Represent the problem with coding function.
- Define the essential parameters
  - Parameters that define the problem.
  - Parameters that store the temporary result or state.
- Define the return value

Fibonacci Number
- Can be solved by DP, which is better
Climbing Stairs
- Same as Fibonacci
Merge Sort
- We will talk more about that in Sort

Classical Recursion Problem

Problem

sub-problem-1

base-problem

sub-problem-2

sub-problem-3

sub-sub-problem-2

sub-sub-sub-problem

sub-sub-problem-1

...

Problem

sub-problem-1

sub-sub-problem

sub-sub-sub-problem

base-problem

Problem

sub-problem-1

base-problem

sub-problem-2

sub-problem-3

sub-sub-problem-2

sub-sub-sub-problem

sub-sub-problem-1

...

Problem

sub-problem-1

sub-sub-problem

sub-sub-sub-problem

base-problem

Problem

sub-problem-1

base-problem

sub-problem-2

sub-problem-3

sub-sub-problem-2

sub-sub-sub-problem

sub-sub-problem-1

...

Problem

sub-problem-1

sub-sub-problem

sub-sub-sub-problem

base-problem

Problem

sub-problem-1

base-problem

sub-problem-2

sub-problem-3

sub-sub-problem-2

sub-sub-sub-problem

sub-sub-problem-1

...

Problem

sub-problem-1

sub-sub-problem

sub-sub-sub-problem

base-problem

Problem

sub-problem-1

base-problem

sub-problem-2

sub-problem-3

sub-sub-problem-2

sub-sub-sub-problem

sub-sub-problem-1

...

Problem

sub-problem-1

sub-sub-problem

sub-sub-sub-problem

base-problem

Problem

sub-problem-1

sub-sub-problem

sub-sub-sub-problem

base-problem

Problem

sub-problem-1

base-problem

sub-problem-2

sub-problem-3

sub-sub-problem-2

sub-sub-sub-problem

sub-sub-problem-1

...

Backtracking

Recursion with one sub problem

Recursion with 1 sub problem does not have to use recursion

We can think about using iteration instead

def factorial(n):
    if n == 1:
        return 1
    return n * factorial(n - 1)

def factorial(n):
    sum = 1
    for i in range(1, n + 1):
        sum = sum * i
    return sum

Gray Code

The gray code is a binary numeral system where two successive values differ in only one bit.

Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.

For example, given n = 2, return [0,1,3,2]

This is a typical problem with only one sub-problem

You need to find the pattern inside of it.

What is gray code: a form of binary that uses a different method of incrementing from one number to the next

Example: 000 001 011 010 110 111 101 100

0 1 3 2 6 7 5 4

Gray Code

The gray code is a binary numeral system where two successive values differ in only one bit.

Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.

For example, given n = 2, return [0,1,3,2]

n=2

n=3

Symmetric

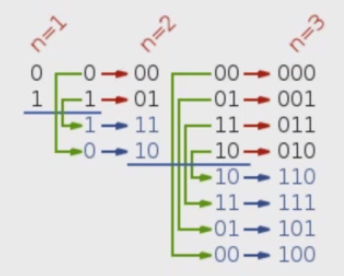
Gray Code

The key is to find the relationship between each sub-problem

def gray_code(n):
    result = []
    helper(n, result)
    return result

def helper(n, result):
    if n == 0:
        result.append(0)
        return
    helper(n - 1, result)
    size = len(result)
    k = 1 << (n - 1)
    for i in range(size - 1, -1, -1):
        result.append(result[i] + k)
    return

Gray Code

    def gray_code(self, n: int) -> List[int]:
        if n == 0:
            return [0]
        res = self.gray_code(n - 1)
        # add = 2 ** (n - 1) # this also works
        add = 1 << (n - 1)
        
        for i in range(len(res) - 1, -1, -1):
            res.append(res[i] + add)
        
        return res

Pow(x, n)

Implement pow(x, n), which calculates x raised to the power n (i.e., xn).

Input: x = 2.00000, n = 10
Output: 1024.00000

Input: x = 2.10000, n = 3

Output: 9.26100

Input: x = 2.00000, n = -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25

Pow(x, n)


    def myPow(self, x: float, n: int) -> float:
        if n == 0:
            return 1
        if n == 1:
            return x

        if n < 0:
            return self.myPow(1 / x, -n)

        if n % 2:
            return self.myPow(x * x, n // 2) * x
        else:
            return self.myPow(x * x, n // 2)

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Example Input:

Start Point: (0, 0); Target Point (5, 5);

Maze: char[][] = {

{'.', 'X', '.', '.', '.', 'X'},

{'.', '.', '.', 'X', '.', 'X'},

{'X', 'X', '.', 'X', '.', '.'},

{'.', 'X', 'X', 'X', '.', 'X'},

{'.', '.', '.', '.', '.', 'X'},

{'.', '.', '.', '.', '.', '.'}

}

Example Output: True

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Example Input:

Start Point: (0, 0); Target Point (5, 5);

Maze: char[][] = {

{'.', 'X', '.', '.', '.', 'X'},

{'.', '.', '.', 'X', '.', 'X'},

{'X', 'X', '.', 'X', '.', '.'},

{'.', 'X', 'X', 'X', '.', 'X'},

{'.', '.', '.', '.', '.', 'X'},

{'.', '.', '.', '.', '.', '.'}

}

Example Output: True

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Consider what are valid subproblem?

What direction can it go?

Out of Bound
Wall

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Out of Bound
Wall
Visited
- (1, 2) -> (2, 2) -> (1, 2) -> (2, 2) -> ...
- Why we cannot go visited place?

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

def solve_maze(maze, startX, startY, targetX, targetY, visited):
    if (startX < 0 or startX >= len(maze) or
        startY < 0 or startY >= len(maze[0]) or
        maze[startX][startY] == 'X' or visited[startX][startY]):
        return False
    if startX == targetX and startY == targetY:
        return True
    visited[startX][startY] = True
    if (solve_maze(maze, startX + 1, startY, targetX, targetY, visited) or
        solve_maze(maze, startX, startY + 1, targetX, targetY, visited) or
        solve_maze(maze, startX - 1, startY, targetX, targetY, visited) or
        solve_maze(maze, startX, startY - 1, targetX, targetY, visited)):
        return True
    return False

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Optimization 1: reuse the maze to reduce the space complexity

def solve_maze(maze, startX, startY, targetX, targetY):
    if (startX < 0 or startX >= len(maze) or
        startY < 0 or startY >= len(maze[0]) or
        maze[startX][startY] == 'X'):
        return False
    if startX == targetX and startY == targetY:
        return True
    maze[startX][startY] = 'X'
    if (solve_maze(maze, startX + 1, startY, targetX, targetY) or
        solve_maze(maze, startX, startY + 1, targetX, targetY) or
        solve_maze(maze, startX - 1, startY, targetX, targetY) or
        solve_maze(maze, startX, startY - 1, targetX, targetY)):
        return True
    return False

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Optimization 2: code style

def solve_maze(maze, startX, startY, targetX, targetY):
    if (startX < 0 or startX >= len(maze) or
        startY < 0 or startY >= len(maze[0]) or
        maze[startX][startY] == 'X'):
        return False
    if startX == targetX and startY == targetY:
        return True
    maze[startX][startY] = 'X'
    dx = [1, 0, -1, 0]
    dy = [0, 1, 0, -1]
    for i in range(4):
        if solve_maze(maze, startX + dx[i], startY + dy[i], targetX, targetY):
            return True
    return False

Maze

Given a maze and a start point and a target point, return whether the target can be reached.

Optimization 3: move the base case -> is it good?

def solve_maze(maze, startX, startY, targetX, targetY):
    if startX == targetX and startY == targetY:
        return True
    maze[startX][startY] = 'X'
    dx = [1, 0, -1, 0]
    dy = [0, 1, 0, -1]
    for i in range(4):
        newX, newY = startX + dx[i], startY + dy[i]
        if (newX < 0 or newX >= len(maze) or
            newY < 0 or newY >= len(maze[0]) or
            maze[newX][newY] == 'X'):
            continue
        if solve_maze(maze, newX, newY, targetX, targetY):
            return True
    return False

Maze

Given a maze and a start point and a target point, print out the path to reach the target.

def solve_maze(maze, startX, startY, targetX, targetY, path):
    if (startX < 0 or startX >= len(maze) or
        startY < 0 or startY >= len(maze[0]) or
        maze[startX][startY] == 'X'):
        return False
    if startX == targetX and startY == targetY:
        print(path)
        return True
    maze[startX][startY] = 'X'
    dx = [1, 0, -1, 0]
    dy = [0, 1, 0, -1]
    direction = ['D', 'R', 'U', 'L']
    for i in range(4):
        newPath = path + direction[i] + " "
        if solve_maze(maze, startX + dx[i], startY + dy[i], targetX, targetY, newPath):
            return True
    return False

Maze

Given a maze and a start point and a target point, return the path to reach the target.

def solve_maze(maze, startX, startY, targetX, targetY, path):
    if (startX < 0 or startX >= len(maze) or
        startY < 0 or startY >= len(maze[0]) or
        maze[startX][startY] == 'X'):
        return False
    if startX == targetX and startY == targetY:
        return True
    maze[startX][startY] = 'X'
    dx = [1, 0, -1, 0]
    dy = [0, 1, 0, -1]
    direction = ['D', 'R', 'U', 'L']
    for i in range(4):
        path.append(direction[i])
        if solve_maze(maze, startX + dx[i], startY + dy[i], targetX, targetY, path):
            return True
        path.pop()
    return False

Maze

Given a maze and a start point and a target point, print out the path to reach the target.

Given a maze and a start point and a target point, return the path to reach the target.

Compare these 2, what is the difference?

When we share the field, what should we do?

Importance for backtracking -> keep the subproblem has the same state

Backtracking Summary

Backtrack = try, iterate, traverse, etc.
Keep trying (in the search space) until
- Solution is found
- No more meaningful methods to try (no more search space)
Level-N problem -> M * Level-(N-1) subproblem
- Keep states the same when entering subproblem for shared fields.

Permutation (Leetcode 46)

Given a collection of distinct numbers, return all possible permutations.

For example,
[1,2,3] have the following permutations:
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1].

public List<List<Integer>> permute(int[] nums) {
// Implement this method.
}

What is the time complexity?

O(n * n!)

Given a collection of distinct numbers, return all possible permutations.

Permutation (Leetcode 46)

Which part is not efficient? -> array contains

def permute(num):
    results = []
    permute_helper(results, [], num)
    return results

def permute_helper(results, cur, num):
    if len(cur) == len(num):
        results.append(list(cur))
        return
    for i in num:
        if i in cur:
            continue
        cur.append(i)
        permute_helper(results, cur, num)
        cur.pop()

Permutation (Leetcode 46)

def permute(num):
    num_list = list(num)
    return permute_helper([], num_list)

def permute_helper(cur, num):
    results = []
    if len(num) == 0:
        results.append(cur)
        return results
    for i in range(len(num)):
        new_cur = cur + [num[i]]
        new_num = num[:i] + num[i+1:]
        results.extend(permute_helper(new_cur, new_num))
    return results

Permutation (Leetcode 46)
How to debug and learn from other solution

def permute(num):
    num_list = list(num)
    return permute_helper([], num_list)

def permute_helper(cur, num):
	print(cur, num)
    results = []
    if len(num) == 0:
        results.append(cur)
        return results
    for i in range(len(num)):
        new_cur = cur + [num[i]]
        new_num = num[:i] + num[i+1:]
        results.extend(permute_helper(new_cur, new_num))
    return results

([], [2, 6, 8])

([2], [6, 8])

([2, 6], [8])

([2, 6, 8], [])

([2, 8], [6])

([2, 8, 6], [])

([6], [2, 8])

([6, 2], [8])

([6, 2, 8], [])

([6, 8], [2])

([6, 8, 2], [])

([8], [2, 6])

([8, 2], [6])

([8, 2, 6], [])

([8, 6], [2])

([8, 6, 2], [])

Permutation II (Leetcode 47)

Given a collection of ~~distinct~~ numbers, return all possible permutations.

def permuteUnique(num):
    results = []
    num.sort()
    visited = [False] * len(num)
    permute(results, [], num, visited)
    return results

def permute(results, cur, num, visited):
    if len(cur) == len(num):
        results.append(list(cur))
        return
    for i in range(len(num)):
        if visited[i] or (i > 0 and num[i] == num[i - 1] and not visited[i - 1]):
            continue
        visited[i] = True
        cur.append(num[i])
        permute(results, cur, num, visited)
        cur.pop()
        visited[i] = False

Permutation II (Leetcode 47)

Given a collection of ~~distinct~~ numbers, return all possible permutations.

def permuteUnique(self, nums):
  results = []
  num = sorted(nums)
  self.permute(results, num, 0)
  return results

def permute(self, results, num, index):
  if index == len(num):
    results.append(num[:])
    return
  for i in range(index, len(num)):
    if i != index and num[index] == num[i]:
      continue
      num[index], num[i] = num[i], num[index]
      self.permute(results, num[:], index + 1)

Combination

Given a collection of distinct numbers, return all possible combinations.

For example,
[2, 6, 8] have the following powersets (combination):
[], [2], [6], [8], [2, 6], [2, 8], [6, 8], [2, 6, 8].

public List<List<Integer>> combine(int[] nums) {
// Implement this method.
}

Combination

Given a collection of distinct numbers, return all possible combinations.

def combine(nums):
    results = []
    combination_helper(results, nums, 0, [])
    return results

def combination_helper(results, nums, index, items):
    if index == len(nums):
        results.append(list(items))
        return
    combination_helper(results, nums, index + 1, items)
    
    items.append(nums[index])
    combination_helper(results, nums, index + 1, items)
    items.pop()

Combination

Given a collection of distinct numbers, return all possible combinations.

def combine(nums):
    results = []
    combination_helper(results, nums, 0, [])
    return results

def combination_helper(results, nums, index, items):
  results.append(list(items))
  if index == len(nums):
    return
  for i in range(index, len(nums)):
    items.append(nums[i])
    combination_helper(results, nums, i + 1, items)
    items.pop()

Lucky Numbers

888 is a lucky number. And for each American phone number, we can actually add some operators to make it become 888. For example:

phone number is 7765332111, you will have

7/7*65*3+3*21*11 = 888

776+5+3*32+11*1 = 888

...

We want to get a full list of all the operation equations that can get a certain lucky number. The interface will be

List<String> luckyNumbers(String num, int target)

Lucky Numbers

We want to get a full list of all the operation equations that can get a certain lucky number. The interface will be

List<String> luckyNumbers(String num, int target)

Additional information:

String num will always be 10 digits since it is a phone number.

we can have "0" but we cannot have "05", "032".

If a number cannot be divided, you cannot use it. For example, 55/2 is not allowed, you need to make sure the division can always be an integer result.

0 cannot be divided.

Lucky Numbers

We need to use recursion to solve the problem

Since we want to output the result. There are things we need to pay attention:

1. The first number does not have operators in front.

2. Use long in case you get the number overflow

3. * and / has higher priority than + and -. How do you handle that?

4. remind 0

Lucky Numbers

def lucky_numbers(num, target):
    result = []
    recursion(num, target, "", 0, 0, 0, result)
    return result

def recursion(num, target, temp, pos, current, last, result):
    if pos == len(num):
        if current == target:
            result.append(temp)
        return
    for i in range(pos, len(num)):
        if num[pos] == '0' and i != pos:
            break
        m = num[pos:i + 1]
        n = int(m)
        if pos == 0:
            recursion(num, target, temp + m, i + 1, n, n, result)
        else:
            recursion(num, target, temp + "+" + m, i + 1, current + n, n, result)
            recursion(num, target, temp + "-" + m, i + 1, current - n, -n, result)
            recursion(num, target, temp + "*" + m, i + 1, current - last + last * n, last * n, result)
            if n != 0 and last % n == 0:
                recursion(num, target, temp + "/" + m, i + 1, current - last + last // n, last // n, result)

Lucky Numbers

Example:

24 + 5 -> current 29, last 5

24 + 5 * 4 -> current 29 - 5 + 20 = 44, last 20

24 + 5 * 4 / 2 -> current 44 - 20 + 10 = 34, last 10

24 + 5 * 4 / 2 - 7 -> current 34 - 7 = 27, last -7

Summary

Recursion

subproblem

-> problem

subproblem-1 ||

subproblem-2 ||

subproblem-N

-> problem

subproblem-1 &&

subproblem-2 &&

subproblem-N

-> problem

Factorial,

Sum of LinkedList,

Remove Linked List Element, etc.

Maze,

Sudoku,

Most DFS problems, etc.

Knapsack

Permutations,

Combinations,

Eight Queen,

kSum, etc.

Summary

Recursion is a strategy.
Always try to split a problem into sub-problems and solve the sub-problem first.
- If the solution is the same, then you can call the same method.

Recursion

What is recursion

Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem (as opposed to iteration).

How to solve a problem

Recursion Properties

Code problem with recursion

Classical Recursion Problem

Recursion with one sub problem

Gray Code

Gray Code

Gray Code

Gray Code

Pow(x, n)

Pow(x, n)

Maze

Maze

Maze

Maze

Maze

Maze

Maze

Maze

Maze

Maze

Maze

Maze

Maze

Backtracking Summary

Permutation (Leetcode 46)

Permutation (Leetcode 46)

Permutation (Leetcode 46)

Permutation (Leetcode 46) How to debug and learn from other solution

Permutation II (Leetcode 47)

Permutation II (Leetcode 47)

Combination

Combination

Combination

Lucky Numbers

Lucky Numbers

Lucky Numbers

Lucky Numbers

Lucky Numbers

Summary

Summary

Permutation (Leetcode 46)
How to debug and learn from other solution