BFS

Breadth First Search
One starts at the root (selecting some arbitrary node as the root in the case of a graph) and explores the neighbor nodes first, before moving to the next level neighbors.
Find minimum path/distance/...
- Minimum Tree Depth
- Word Edit Distance
- etc...
No Recursion, QUEUE

Queue

Used for BFS
FIFO
VS Stack?
Multitask Queue / System queue -> Design

Queue in Java

Queue<> queue = new LinkedList<>();
- boolean offer(Element e); (add)
  - offer can return false while add can only cause exception when the element cannot be added due to capacity restriction.
- Element poll(); (remove)
  - poll returns null when empty while remove will throw exception.
- Element peek(); (element)
  - peek returns null when empty while element will throw exception.

Queue in Python

from collections import deque

# Creating a queue
queue = deque()

# Adding elements to the queue
queue.append('element1') # Similar to offer in Java
queue.append('element2')

# Removing elements from the queue
element = queue.popleft() # Similar to poll in Java; use pop() for a stack
if not queue:
print("Queue is empty")

# Peeking at the front of the queue
if queue:
front = queue[0] # Similar to peek in Java
print("Front element:", front)
else:
print("Queue is empty, nothing to peek")

BFS for Binary Trees

Binary Tree Level Order Traversal

/ \

B C

/ \ / \

D E F G

/ \

H I

Given a binary tree, return its level order traversal.

def level_order_traversal(root):
    queue = deque([root])  # Initialize the queue with the root

    while queue:
        top = queue.popleft()  # Pop from the front of the queue

        # visit top (can be replaced with any operation)
        print(top.val)  # Example visit operation

        if top.left:
            queue.append(top.left)  # Add left child to queue if exists

        if top.right:
            queue.append(top.right)  # Add right child to queue if exists

Binary Tree Level Order Traversal

/ \

B C

/ \ / \

D E F G

/ \

H I

Given a binary tree, return its level order traversal.

The output is A B C D E F G H I

What if we want to separate each level?

Binary Tree Level Order Traversal

Given a binary tree, return its level order traversal.

[
  [3],
  [9,20],
  [15,7]
]

Binary Tree Level Order Traversal

Given a binary tree, return its level order traversal.

def levelOrder(root):
    results = []
    queue = []
    if root is not None:
        queue.append(root)
    while len(queue) > 0:
        oneResult = []
        queue2 = []
        while len(queue) > 0:
            top = queue.pop(0)
            if top.left is not None:
                queue2.append(top.left)
            if top.right is not None:
                queue2.append(top.right)
            oneResult.append(top.val)
        results.append(oneResult)
        queue = queue2
    return results

Binary Tree Level Order Traversal

def levelOrder(root):
    if not root:
        return []
    results = []
    queue = []
    queue.append(root)
    queue.append(None)
    oneResult = []
    while len(queue) > 0:
        top = queue.pop(0)
        if top is None:
            results.append(oneResult)
            if len(queue) > 0:
                queue.append(None)
            oneResult = []
        else:
            if top.left is not None:
                queue.append(top.left)
            if top.right is not None:
                queue.append(top.right)
            oneResult.append(top.val)
    return results

Binary Tree Level Order Traversal

def levelOrder(root):
    results = []
    queue = []
    size = 1
    nextSize = 0
    if root is not None:
        queue.append(root)
    oneResult = []
    while queue:
        top = queue.pop(0)
        if top.left is not None:
            queue.append(top.left)
            nextSize += 1
        if top.right is not None:
            queue.append(top.right)
            nextSize += 1
        oneResult.append(top.val)
        size -= 1
        if size == 0:
            results.append(oneResult)
            oneResult = []
            size = nextSize
            nextSize = 0
    return results

Binary Tree Zigzag Level Order Traversal

Given a binary tree, return its zigzag level order traversal.

[
  [3],
  [20,9],
  [15,7]
]

Binary Tree Zigzag Level Order Traversal

def zigzagLevelOrder(root):
    results = []
    queue = []
    if root is not None:
        queue.append(root)
    isOdd = True
    while len(queue) > 0:
        oneResult = []
        queue2 = []
        while len(queue) > 0:
            top = queue.pop(0)
            if top.left is not None:
                queue2.append(top.left)
            if top.right is not None:
                queue2.append(top.right)
            oneResult.append(top.val)
        if not isOdd:
            oneResult.reverse()
        results.append(oneResult)
        isOdd = not isOdd
        queue = queue2
    return results

Binary Tree Zigzag Level Order Traversal

Reversing an ArrayList for every loop is time-consuming. It is really time consuming?
What is the run time?
Visit order is opposite from level to level
- LIFO
- Stack

def zigzagLevelOrder(root):
    results = []
    if root is None:
        return results
    stack = []
    stack.append(root)
    isOdd = True
    while len(stack) > 0:
        oneResult = []
        stack2 = []
        while len(stack) > 0:
            top = stack.pop()
            if not isOdd:
                if top.right is not None:
                    stack2.append(top.right)
                if top.left is not None:
                    stack2.append(top.left)
            else:
                if top.left is not None:
                    stack2.append(top.left)
                if top.right is not None:
                    stack2.append(top.right)
            oneResult.append(top.val)
        results.append(oneResult)
        stack = stack2
        isOdd = not isOdd
    return results

[
  [3],
  [20,9],
  [15,7]
]

Find Bottom Left Tree Value

BFS

Same as level traversal, but need to know which one is the first one of this level

Given a binary tree, find the leftmost value in the last row of the tree.

Result: 4

Find Bottom Left Tree Value

def findBottomLeftValue(root):
    queue = []
    queue.append(root)
    leftValue = 0
    isFirst = False
    while queue:
        isFirst = True
        queue2 = []
        while queue:
            top = queue.pop(0)
            if isFirst:
                leftValue = top.val
                isFirst = False
            if top.left:
                queue2.append(top.left)
            if top.right:
                queue2.append(top.right)
        queue = queue2
    return leftValue

How to level order traverse

If level is important, most cases
- Two queues.
- Dummy node, different from all other nodes to be a flag.
- Maintain size of current level.
If level is unimportant
- One queue.

Minimum Depth of Binary Tree

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Minimum Depth of Binary Tree

DFS

Minimum depth of Root
- if root is leaf, 1.
- if root.left is null, return right.
- if root.right is null, return left.
- return the minimum of (left, right).

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Minimum Depth of Binary Tree

BFS

Level Traverse the tree, return the depth of the first leaf node.

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Minimum Depth of Binary Tree

def minDepth(root):
    if root is None:
        return 0
    queue = []
    queue.append(root)
    queue.append(None)
    minDepth = 1
    while len(queue) > 0:
        top = queue.pop(0)
        if top is None:
            minDepth += 1
            queue.append(None)
            continue
        if top.left is None and top.right is None:
            return minDepth
        if top.left is not None:
            queue.append(top.left)
        if top.right is not None:
            queue.append(top.right)
    return minDepth

Minimum Depth of Binary Tree

def minDepth(root):
    if root is None:
        return 0
    queue = []
    queue.append(root)
    minDepth = 1
    while len(queue) > 0:
        queue2 = []
        while len(queue) > 0:
            top = queue.pop(0)
            if top.left is None and top.right is None:
                return minDepth
            if top.left is not None:
                queue2.append(top.left)
            if top.right is not None:
                queue2.append(top.right)
        minDepth += 1
        queue = queue2
    return minDepth

DFS, BFS which one is better ?

Level is important, most cases
- Two queues.
- Dummy node, different from all other nodes to be a flag.
- Maintain size of current level.
Level is unimportant
- One queue.
Don't add null (except dummy) into queues.
Left/Right null pointer check.

BFS for Binary Trees

General BFS

Simple Maze

We can solve using DFS

We can also do it in BFS

Simple Maze

Queue setup:

2 dimension ->

1 dimension

from collections import deque

def solveMaze(maze, startX, startY, targetX, targetY, visited):
    queue = deque()
    
    xLen, yLen = len(maze), len(maze[0])
    dx = [-1, 0, 1, 0]
    dy = [0, 1, 0, -1]

    queue.append(startX * yLen + startY)
    visited[startX][startY] = True

    while queue:
        temp = queue.popleft()
        for i in range(4):
            nx = temp // yLen + dx[i]
            ny = temp % yLen + dy[i]
            if nx == targetX and ny == targetY:
                return True
            if 0 <= nx < xLen and 0 <= ny < yLen and maze[nx][ny] == 'O' and not visited[nx][ny]:
                visited[nx][ny] = True
                queue.append(nx * yLen + ny)

    return False

There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the ball's start position, the destination and the maze, find the shortest distance for the ball to stop at the destination. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included). If the ball cannot stop at the destination, return -1.

The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.

The Maze II

the biggest difference: This time the ball not always goes only 1 step.

Example 1
Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: 12

The Maze II

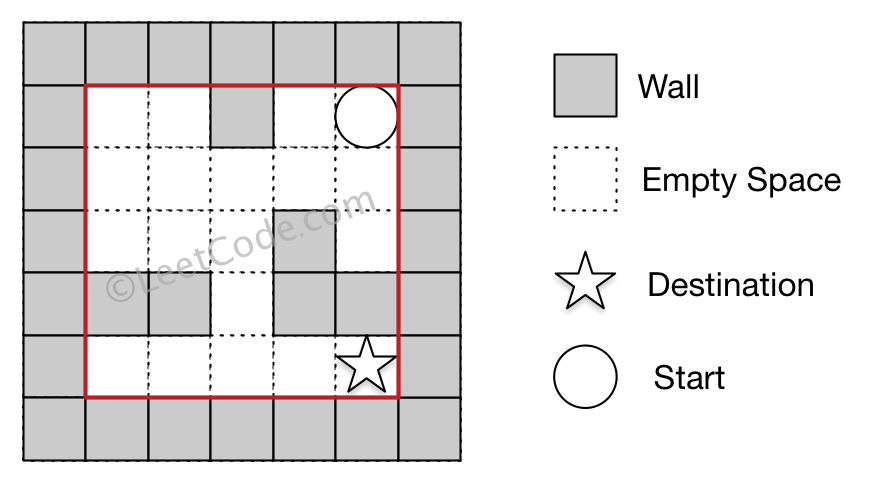
Explanation: One shortest way is :

left -> down -> left -> down -> right -> down -> right. The total distance is

1 + 1 + 3 + 1 + 2 + 2 + 2 = 12.

We need to use BFS to solve the problem since it wants to get the shortest way. And BFS could simulate the behavior well.

The most important thing is to let the queue mock the action that the ball will continue rolling till it hits the edge or a block.

As long as we can mock this operation, it will be much easier for us to solve the problem.

How do we simulate this operation?

For each step we pop from queue, we need to use a while loop to keep rolling the ball till the end

The Maze II

def shortestDistance(self, maze, start, dest):
    row = len(maze)
    col = len(maze[0])
    distance = [[float('inf') for _ in range(col)] for _ in range(row)]
    dx = [1, 0, 0, -1]
    dy = [0, -1, 1, 0]
    queue = []
    queue.append(Pair(start[0], start[1]))
    distance[start[0]][start[1]] = 0

    while queue:
        current = queue.pop(0)
        for i in range(4):
            x = current.x
            y = current.y
            dist = distance[x][y]
            while x >= 0 and x < row and y >= 0 and y < col and maze[x][y] == 0:
                x += dx[i]
                y += dy[i]
                dist += 1
            x -= dx[i]
            y -= dy[i]
            dist -= 1
            if distance[x][y] > dist:
                distance[x][y] = dist
                if x != dest[0] or y != dest[1]:
                    queue.append(Pair(x, y))

    res = distance[dest[0]][dest[1]]
    return -1 if res == float('inf') else res

The Maze II

class Pair:
    def __init__(self, x, y):
        self.x = x
        self.y = y

There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up (u), down (d), left (l) or right (r), but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction. There is also a hole in this maze. The ball will drop into the hole if it rolls on to the hole.

Given the ball position, the hole position and the maze, your job is to find out how the ball could drop into the hole by moving shortest distance in the maze. The distance is defined by the number of empty spaces the ball go through from the start position (exclude) to the hole (include). Output the moving directions by using 'u', 'd', 'l' and 'r'. Since there may have several different shortest ways, you should output the lexicographically smallest way. If the ball cannot reach the hole, output "impossible".

The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The ball and hole coordinates are represented by row and column indexes.

The Maze III

Example:

Input 1: a maze represented by a 2D array

0 0 0 0 0
1 1 0 0 1
0 0 0 0 0
0 1 0 0 1
0 1 0 0 0

Input 2: ball coordinate (rowBall, colBall) = (4, 3)
Input 3: hole coordinate (rowHole, colHole) = (0, 1)

Output: "lul"
Explanation: There are two shortest ways for the ball to drop into the hole.
The first way is left -> up -> left, represented by "lul".
The second way is up -> left, represented by 'ul'.
Both ways have shortest distance 6, but the first way is lexicographically smaller because 'l' < 'u'. So the output is "lul".

The Maze III

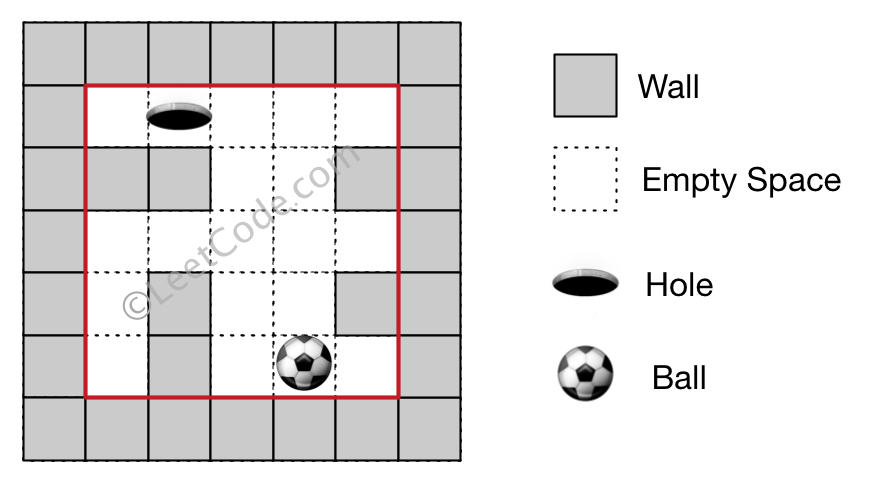
We still need to use BFS to solve the problem.

We need to use a Path to keep the result since even within the same shortest way, we want to output the smallest one in lexicographical order.

The other part is very similar to The Maze II. But one thing to keep in mind:

If you hit the destination, since it is a trap, you can stop immediately instead of keeping rolling foward.

The Maze III

def findShortestWay(self, maze, ball, hole):
    row = len(maze)
    col = len(maze[0])
    dx = [1, 0, 0, -1]
    dy = [0, -1, 1, 0]
    dir = ["d", "l", "r", "u"]
    distance = [[float('inf')] * col for _ in range(row)]

    distance[ball[0]][ball[1]] = 0
    queue = [(ball[0], ball[1])]
    path = [[""] * col for _ in range(row)]
    path[ball[0]][ball[1]] = ""

    while queue:
        cur = queue.pop(0)

        for i in range(4):
            x, y = cur[0], cur[1]
            dist = distance[x][y]
            currentPath = path[x][y]

            while x >= 0 and x < row and y >= 0 and y < col and maze[x][y] == 0 and (x != hole[0] or y != hole[1]):
                x += dx[i]
                y += dy[i]
                dist += 1

            if x != hole[0] or y != hole[1]:
                x -= dx[i]
                y -= dy[i]
                dist -= 1

            newPath = currentPath + dir[i]

            if distance[x][y] > dist or (distance[x][y] == dist and path[x][y] > newPath):
                distance[x][y] = dist
                path[x][y] = newPath

                if x != hole[0] or y != hole[1]:
                    queue.append((x, y))

    result = path[hole[0]][hole[1]]
    return "impossible" if distance[hole[0]][hole[1]] == float('inf') else result

Given two words (beginWord and endWord), and a dictionary's word list, find the length of shortest transformation sequence from beginWord to endWord, such that:

Only one letter can be changed at a time
Each intermediate word must exist in the word list

For example,
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.

Note:

Return 0 if there is no such transformation sequence.
All words have the same length.
All words contain only lowercase alphabetic characters.

Word Ladder

DFS

begin: hot, end: hip, list: [hog, hig, dig, dip, hip, hit]
hot -> hog -> hig -> dig -> dip -> hip
Much deeper than needed, time consuming.

BFS

Keep a set of all words that can be transformed to.
Put all words with 1 edit distance into the set every time.
When the end word is met, then the minimum distance is found.

Word Ladder

BFS
- Keep a set of all words that can be transformed to.
- Put all words with 1 edit distance into the set every time.
- When the end word is met, then the minimum distance is found.

Word Ladder

beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

BFS
- Keep a set of all words that can be transformed to.
- Put all words with 1 edit distance into the set every time.
- When the end word is added, then the minimum distance is found.

Word Ladder

beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

BFS
- Keep a set of all words that can be transformed to.
- Put all words with 1 edit distance into the set every time.
- When the end word is added, then the minimum distance is found.

Word Ladder

beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

dot

lot

BFS
- Keep a set of all words that can be transformed to.
- Put all words with 1 edit distance into the set every time.
- When the end word is added, then the minimum distance is found.

Word Ladder

beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

dot

lot

dog

log

BFS
- Keep a set of all words that can be transformed to.
- Put all words with 1 edit distance into the set every time.
- When the end word is added, then the minimum distance is found.

Word Ladder

beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

dot

lot

dog

log

cog

Word Ladder

transformed_words <- beginWord

while (transformed_words is not empty) {

for (word_b in transformed_words) {

if (endWord is within 1 distance) {

return distance

}

if (some word in dict is within 1 distance

&& it is not in transformed_words) {

transformed_words.add(word)

}

update distance

}

return 0

How to check?

Word Ladder

transformed_words <- beginWord

while (transformed_words is not empty) {

for (word_b in transformed_words) {

if (endWord is within 1 distance) {

return distance

}

if (some word in dict is within 1 distance

&& it is not in transformed_words) {

transformed_words.add(word)

}

update distance

}

return 0

How to check?

Word Ladder

transformed_words <- beginWord

while (transformed_words is not empty) {

for (word_b in transformed_words) {

if (endWord is within 1 distance) {

return distance

}

if (some word in dict is within 1 distance

&& it is not in transformed_words) {

transformed_words.add(word)

}

update distance

}

return 0

How to check?

Word Ladder

 def ladderLength(beginWord, endWord, wordList):
    wordSet = set(wordList)
    queue = []
    queue.append(beginWord)
    visited = set()
    visited.add(beginWord)
    distance = 1
    while queue:
        queue2 = []
        distance += 1
        while queue:
            top = queue.pop(0)
            wordsWithinDistance = getWordsWithinDistance(wordSet, top)
            for word in wordsWithinDistance:
                if word == endWord:
                    return distance
                if word not in visited:
                    queue2.append(word)
                    visited.add(word)
        queue = queue2
    return 0

Word Ladder

def getWordsWithinDistance(wordSet, word):
    results = []
    wordCharArr = list(word)
    for i in range(len(word)):
        oriChar = wordCharArr[i]
        for c in range(ord('a'), ord('z')+1):
            if c == ord(oriChar):
                continue
            wordCharArr[i] = chr(c)
            newStr = ''.join(wordCharArr)
            if newStr in wordSet:
                results.append(newStr)
        wordCharArr[i] = oriChar
    return results

Word Ladder

def ladderLength(beginWord, endWord, wordList):
    wordSet = set(wordList)
    queue = [beginWord]
    distance = 1
    
    while queue and wordSet:
        queue2 = []
        distance += 1
        
        while queue:
            top = queue.pop(0)
            wordsWithinDistance = getWordsWithinDistance(wordSet, top)
            
            if endWord in wordsWithinDistance:
                return distance
            
            queue2.extend(wordsWithinDistance)
        
        queue = queue2
    
    return 0

Word Ladder

def getWordsWithinDistance(wordSet, word):
    results = []
    wordCharArr = list(word)
    
    for i in range(len(word)):
        oriChar = wordCharArr[i]
        
        for c in 'abcdefghijklmnopqrstuvwxyz':
            if c == oriChar:
                continue
            wordCharArr[i] = c
            newStr = ''.join(wordCharArr)
            if newStr in wordSet:
                results.append(newStr)
                wordSet.remove(newStr)
        
        wordCharArr[i] = oriChar
    
    return results

访问过的可以在wordSet删掉，已经在results保存，下次也不需要再check

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

Example:

beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

Return

  [
    ["hit","hot","dot","dog","cog"],
    ["hit","hot","lot","log","cog"]
  ]

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

Example:

beginWord = "hit"

endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

Example:

beginWord = "hit"

endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

Example:

beginWord = "hit"

endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

dot

lot

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

Example:

beginWord = "hit"

endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

dot

lot

dog

log

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

Example:

beginWord = "hit"

endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

dot

lot

dog

log

cog

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

Example:

beginWord = "hit"

endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

dot

lot

dog

log

cog

Visited needs to be updated after one level.
wordList need to be updated after one level.

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

Example:

beginWord = "hit"

endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

hit

hot

dot

lot

dog

log

cog

Path needs to be recorded backwards.
HashMap<String, ArrayList<String>>

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

BFS to get shortest transformation
Record the path information during transformation so that the sequence can get regenerated later.
- with visited set, all nodes on the path can guarantee the shortest distance.
DFS to get all the transformation sequences
- backward from endWord instead of forward from startWord

Word Ladder II

def findLadders(beginWord, endWord, wordList):
    wordSet = set(wordList)
    results = []
    preList = {}
    
    queue = [beginWord]
    visited = set()
    visited.add(beginWord)
    
    while queue and wordList:
        queue2 = set()
        isFinished = False
        
        while queue:
            top = queue.pop(0)
            wordsWithinDistance = getWordsWithinDistance(wordList, top)
            
            for word in wordsWithinDistance:
                if word == endWord:
                    isFinished = True
                if word not in visited:
                    updatePreList(preList, word, top)
                    queue2.add(word)
        
        visited.update(queue2)
        
        if isFinished:
            getPaths(results, preList, [], endWord)
            break
        
        queue.extend(queue2)
    
    return results

Word Ladder II

def updatePreList(preList, cur, pre):
    if cur not in preList:
        preList[cur] = []
    preList[cur].append(pre)

def getWordsWithinDistance(wordSet, word):
    results = set()
    wordCharArr = list(word)
    
    for i in range(len(word)):
        oriChar = wordCharArr[i]
        
        for c in 'abcdefghijklmnopqrstuvwxyz':
            if c == oriChar:
                continue
            wordCharArr[i] = c
            newStr = ''.join(wordCharArr)
            if newStr in wordSet:
                results.add(newStr)
        
        wordCharArr[i] = oriChar
    
    return results

Word Ladder II

How to get paths backward from endWord?
- DFS (recursion)
  - Base Case: endWord.pre == null
  - Recursion rule: path from endWord = path from endWord.pre + endWord

Word Ladder II

def getPaths(paths, preList, curPath, end):
    # Base case: if this word has no predecessors
    if end not in preList:
      curPath.append(end)
      curPath.reverse()          # reverse since we built backwards
      paths.append(curPath)      # add one complete path
      return

    # Recursive case: expand all predecessors
    for pre in preList[end]:
      newPath = curPath.copy()   # copy current partial path
      newPath.append(end)        # extend with current word
      getPaths(paths, preList, newPath, pre)

Word Ladder II

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord

BFS to get shortest transformation
Record the paths from beginning while BFSing
Add only the valid paths into results.

Distance means level important
- Two queues
Pruning for duplicate word
- HashSet for visited words
- Remove from dict.

BFS for Word Distance

Both complete search
DFS is recursion
- stack
- better at checking connection, etc.
BFS is iteration
- queue
- better at minimum distance, etc.
Many problems are both solvable by DFS/BFS
- Surrounded Region
- Number of Islands
- etc.

DFS v.s. BFS

Given a 2D board containing 'X' and 'O', capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Surrounded Region

X X X X
X O O X
X X O X
X O X X

X X X X
X X X X
X X X X
X O X X

Given a 2D board containing 'X' and 'O', capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Surrounded Region

def solve(board):
    if len(board) == 0 or len(board[0]) == 0:
        return
    
    for j in range(len(board[0])):
        search(board, 0, j)
        search(board, len(board) - 1, j)
    
    for i in range(len(board)):
        search(board, i, 0)
        search(board, i, len(board[0]) - 1)
    
    for i in range(len(board)):
        for j in range(len(board[0])):
            board[i][j] = 'O' if board[i][j] == 'F' else 'X'

Given a 2D board containing 'X' and 'O', capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Surrounded Region

# BFS
def search(board, x, y):
    if board[x][y] == 'X':
        return
    
    queue = []
    xLen = len(board)
    yLen = len(board[0])
    dx = [-1, 0, 1, 0]
    dy = [0, 1, 0, -1]
    
    queue.append(x * yLen + y)
    board[x][y] = 'F'
    
    while queue:
        temp = queue.pop(0)
        for i in range(4):
            nx = temp // yLen + dx[i]
            ny = temp % yLen + dy[i]
            if nx >= 0 and nx < xLen and ny >= 0 and ny < yLen and board[nx][ny] == 'O':
                board[nx][ny] = 'F'
                queue.append(nx * yLen + ny)

Given a 2D board containing 'X' and 'O', capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Surrounded Region

# DFS
def search(board, i, j):
    if board[i][j] != 'O':
        return
    board[i][j] = 'F'
    if i > 1:
        search(board, i - 1, j)
    if i < len(board) - 2:
        search(board, i + 1, j)
    if j > 1:
        search(board, i, j - 1)
    if j < len(board[i]) - 2:
        search(board, i, j + 1)