Emergence of Collective Behaviors in Hub-Based Colonies using
Grammatical Evolution
and
Behavior Trees
Aadesh Neupane
Problem
- Designing collective behaviors is cumbersome
- Requires experts for modeling
Solution
- Evolutionary computation to generate collective behaviors
$$\frac{dR}{dt} = -aR + vnD , R(0) = R_0$$
$$\frac{dO}{dt} = aR -bO +cE, O(0) = O_0$$
$$\frac{dE}{dt} = q(D)bO - cE, E(0) = E_0$$
$$\frac{dA}{dt} = p(D)bO - mA + wnD$$
$$\frac{dD}{dt} = mA - nD, D(0) = D_0$$
Reference: Stability of choice in the honey bee nest-site selection process

Presentation Structure
- Demo
- Related work
- GEESE
- Challenges
- Validation
- Summary
Real Ants
Demo
Single Source Foraging
Demo
Cooperative Transport
Demo
Nest Maintenance
Related Work - Evolutionary Robotics
Reference: Evolution of collective behaviors for a real swarm of aquatic surface robots
- Swarm behaviors like homing, dispersion, clustering and monitoring by Duarte et. at
- Validation of scalability, flexibility, and robustness on transferred controller
Neural Network based controllers
Merits
- Easy mapping from sensory inputs into actuators values
- Provides generalized solutions
- Only a few human inputs needed
Demerits
- Issues with reverse engineering
- Insights on collective behavior difficult
- Almost impossible to modify the behaviors
Related Work - Evolutionary Robotics
Reference: GESwarm: Grammatical Evolution for the Automatic Synthesis of Collective Behaviors in Swarm Robotics
- Foraging problem using GE by Ferrante et. al.
- Preconditions, low-level behavior and actions gave behaviors
Grammatical Evolution (GE) based controllers
Advantages
Disadvantages
- BNF grammar and objective function
- Analyzing and modifying collective behaviors easier
- Primitive low-level rules defined by experts
- Mapping to raw sensors and actuators values difficult
Related Work - Behavior Tree
Reference: Behavior Trees for Evolutionary Robotics
DelFly Explorer
Related Work - Evolution
Reference: odNEAT: An algorithm for distributed online, onboard evolution of robot behaviours
odNEAT
- Online distributed evolution of Neural networks
- Applicable for online learning in groups of embodied agents (robots)
- Performs well in aggregation task
Combination of best features from all these works?
- A multi-agent Grammatical Evolution with BT
GEESE


















GEESE





Hello! Neighbour!
How are you doing with the phenotype in this environment?
Hello!
I collected 35 oz of water with the phenotype.
Take my genome and perform magic using genetic operators !
Agent

Initialization

GEESE Pipeline

Simulator

BNF Grammar - Swarms

Swarm Behaviors




Composite Carry
Composite Drop
Move Towards
Explore
Challenges
Non-episodic learning

Partially observable

Huge search space
Credit Assignment
Solution - Fitness Functions
Task-Specific
- Foraging : Total food collection in hub
- Cooperative Transport : Total heavy object collected in hub
- Nest Maintenance : Total debris removed from hub
Spatial
- Exploration : Area explored
- Prospective : Total objects carried
Diversity
- Phenotypic Diversity : Total unique behaviors
Thesis Statement
The interaction of hundreds of agents within the framework of distributed grammatical evolution will increase the effectiveness of evolving collective behaviors of bio-swarms. The evolved behaviors can be reused for different collective problems that have similar properties. Furthermore, with a slight variation of the objective function, the same set of primitive behaviors, encoded in the grammar, can lead to collective behaviors over a wider range of collective problems.
Validation
| Claim | Metric |
|---|---|
| Effectiveness | Quality solutions in fewer generations |
| Robustness | Same behavior for both single and multiple foraging problem |
| Breadth |
Solutions for Foraging and cooperative transport problem |
Validation

Effectiveness

Validation
Effectiveness
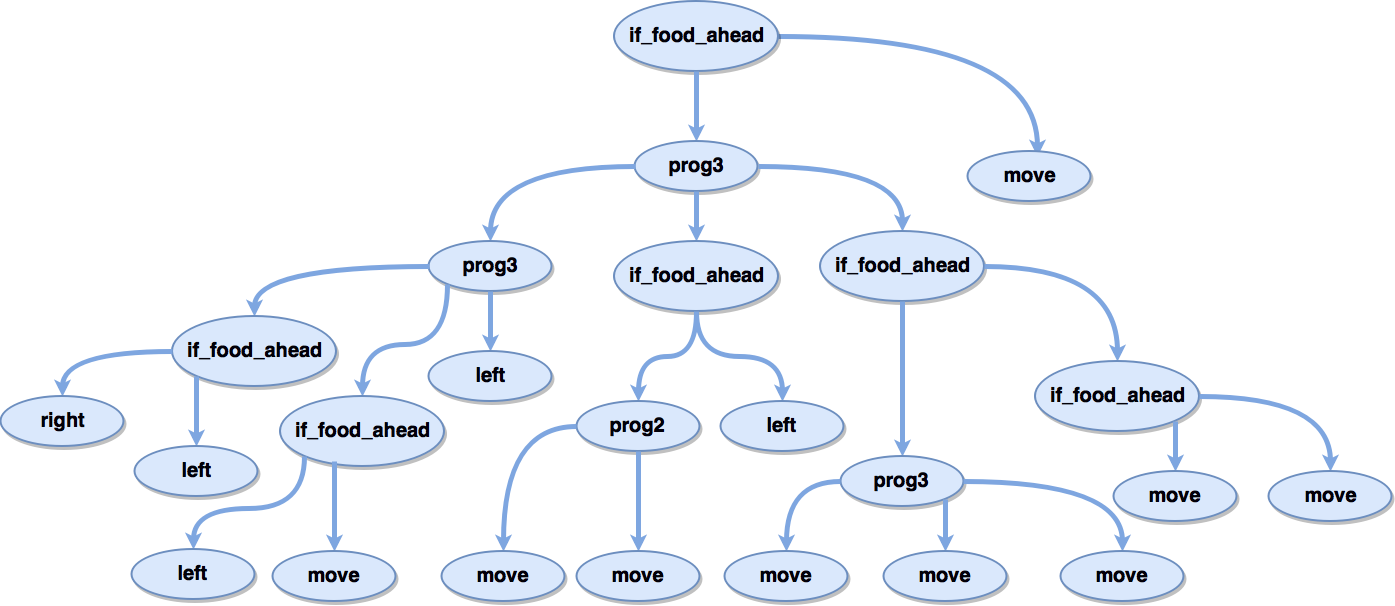
Solves the Santa Fe Trail in 324 steps
GE [Novelty] solved in 331 steps
Validation
- Breadth
Cooperative Transport
Nest Maintenance


Cooperative Transport
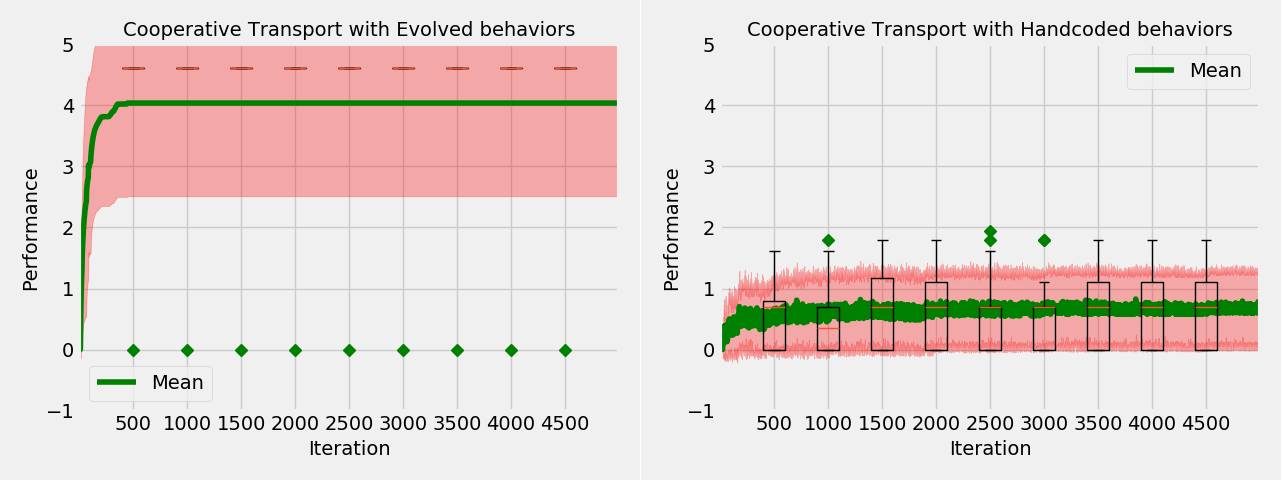
Nest Maintanence

Interesting Foraging Behavior
Interesting Nest Maintenance behavior
Summary
| Claims from thesis | Evidence |
|---|---|
| Effectiveness | Least number of steps for SantaFe Trail problem. |
| Robustness | Transferability of evolved behaviors in foraging problems |
| Breadth | Applicability of same BNF grammar for different swarm tasks |
| Novelty | Combination of GE with BT |
Future Work
-
General
- Test in actual robots
- Probabilistic modeling
-
Learning
- Solve regression and classification tasks
- General consensus decision-making
-
Swarms
- Interference effects
- Analysis of behavioral diversity and diversity heuristic
Acknowledgement
This work has been funded by ONR grant number N000141613025.