Computational Biology Seminar

Class 05 - Storytelling

(BIOSC 1630)

September 27, 2023

Towards Atomistic Modeling of Complex Environments with Many-Body Machine Learning Potentials

Alex M. Maldonado

aalexmmaldonado

Maldonado, A. M.; et al. Digital Discovery 2023, 2, 871-880. DOI: 10.1039/D3DD00011G

Clean energy is growing, but slowly

Solvation plays an important role in advancing energy technologies

Nuclear power

Molten salts

Nuclear Reactor by Olena Panasovska from Noun Project

Batteries

Electrolyte by M. Oki Orlando from Noun Project

Charge carriers and electrolytes

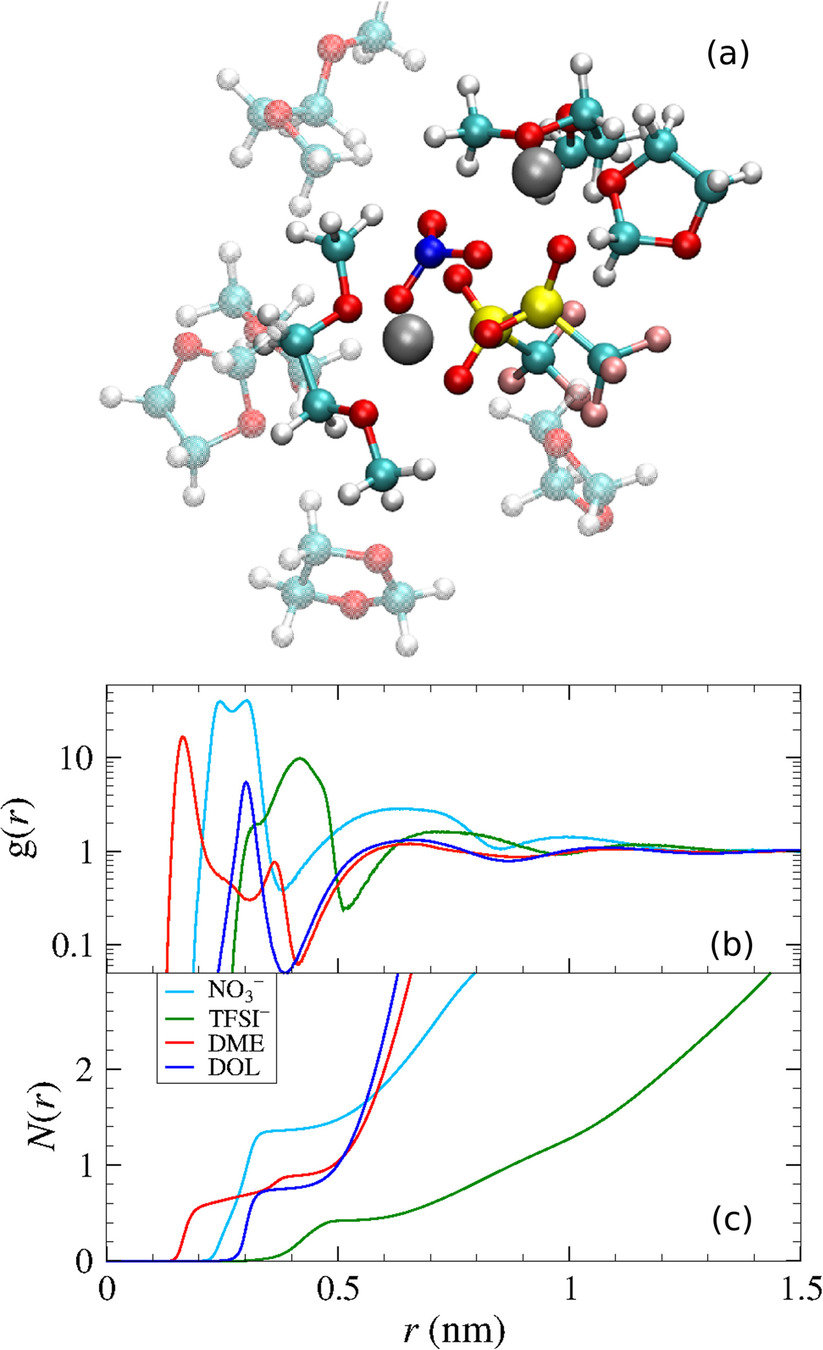
Park, C.; et al. J. Power Sources 2018, 373, 70-78. DOI: 10.1016/j.jpowsour.2017.10.081

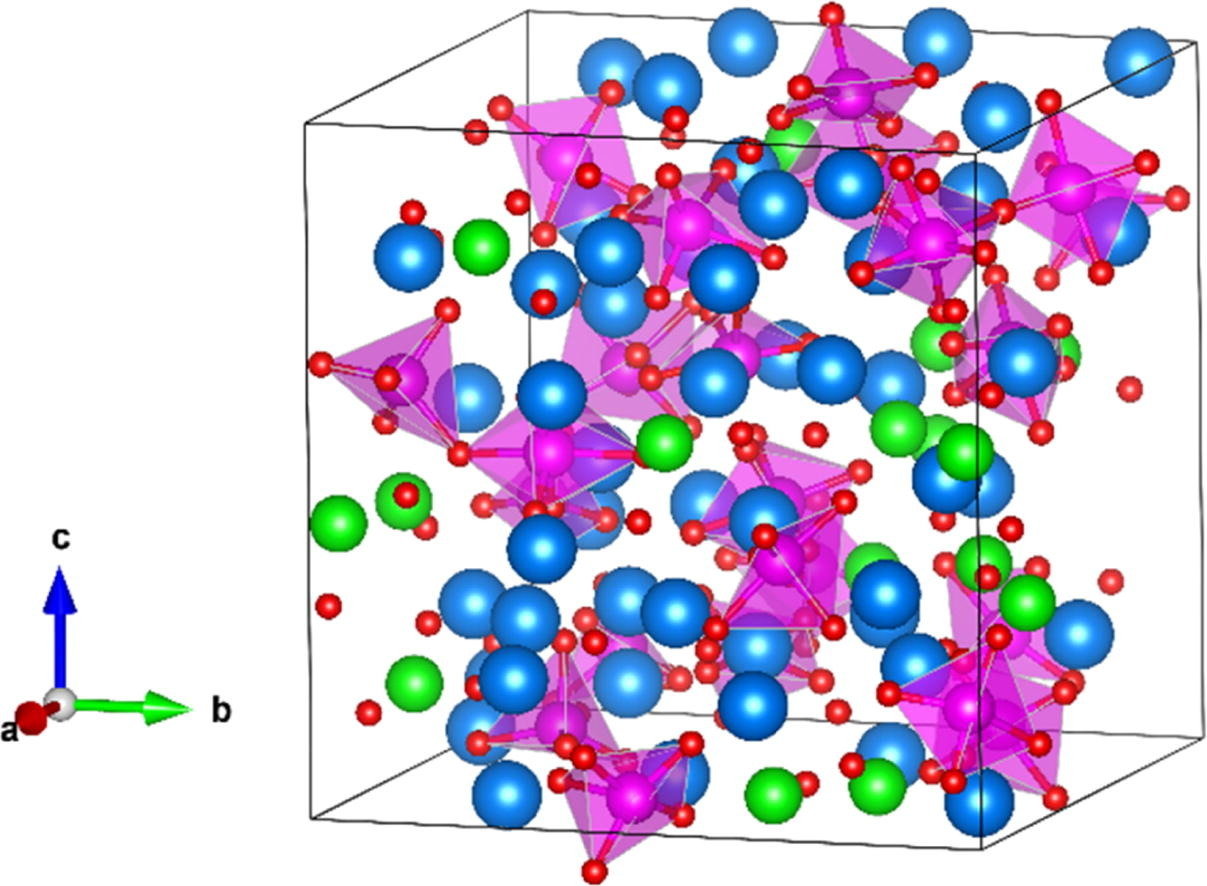
Lv, X.; et al. Chem. Phys. Lett. 2018, 706, 237-242. DOI: 10.1016/j.cplett.2018.06.005

Fuel production

Catalysts

Ma, C.; et al. ACS Catal. 2012, 373, 1500-1506. DOI: 10.1021/cs300350b

Complex simulations are hindered by our current force fields

Lv, X.; et al. Chem. Phys. Lett. 2018, 706, 237-242. DOI: 10.1016/j.cplett.2018.06.005

Let's model a molten salt

Pro: Fast

Con: Parameters

Classical potential

Quantum chemistry

Pro: Accurate

Con: Cost

DFT

N^{3-4}

MP2

N^5

CCSD(T)

N^7

Confidence

Confident predictions require explicit molecular simulations

Computational modeling

Cost

AIMD

Classical MD

Implicit/explicit

Implicit

Confidence

Cost

Screening

approach

Promising candidates

Search space

without experimental data

Solvation treatments

Goal

Machine learning potentials accelerate quantum chemical predictions

Structure

ML potential

Energy and forces

Quantum

chemistry

Machine learning potentials accelerate quantum chemical predictions

Most ML force fields use per-atom contributions

Calculate total energies with QC

Training a typical ML potential

Sample tens of thousands of configurations

Approximation: atomic contributions can reproduce total energy

Examples: DeePMD, GAP, SchNet, PhysNet, ANI, . . .

E_{total} \approx \sum\limits^{N_{atoms}} \varepsilon_i

Known

Learned

with a local descriptor

Global descriptors provide superior data efficiency

Local

Global

Encodes each

atom

Encodes entire

structure

Many descriptors and parameters

Single descriptor

Training on force enables better force field interpolation

Training on forces provides more information about the geometry and energy relationship

Chimiela, S. ; et al. Sci. Adv. 2017, 3 (5), e1603015. DOI: 10.1126/sciadv.1603015

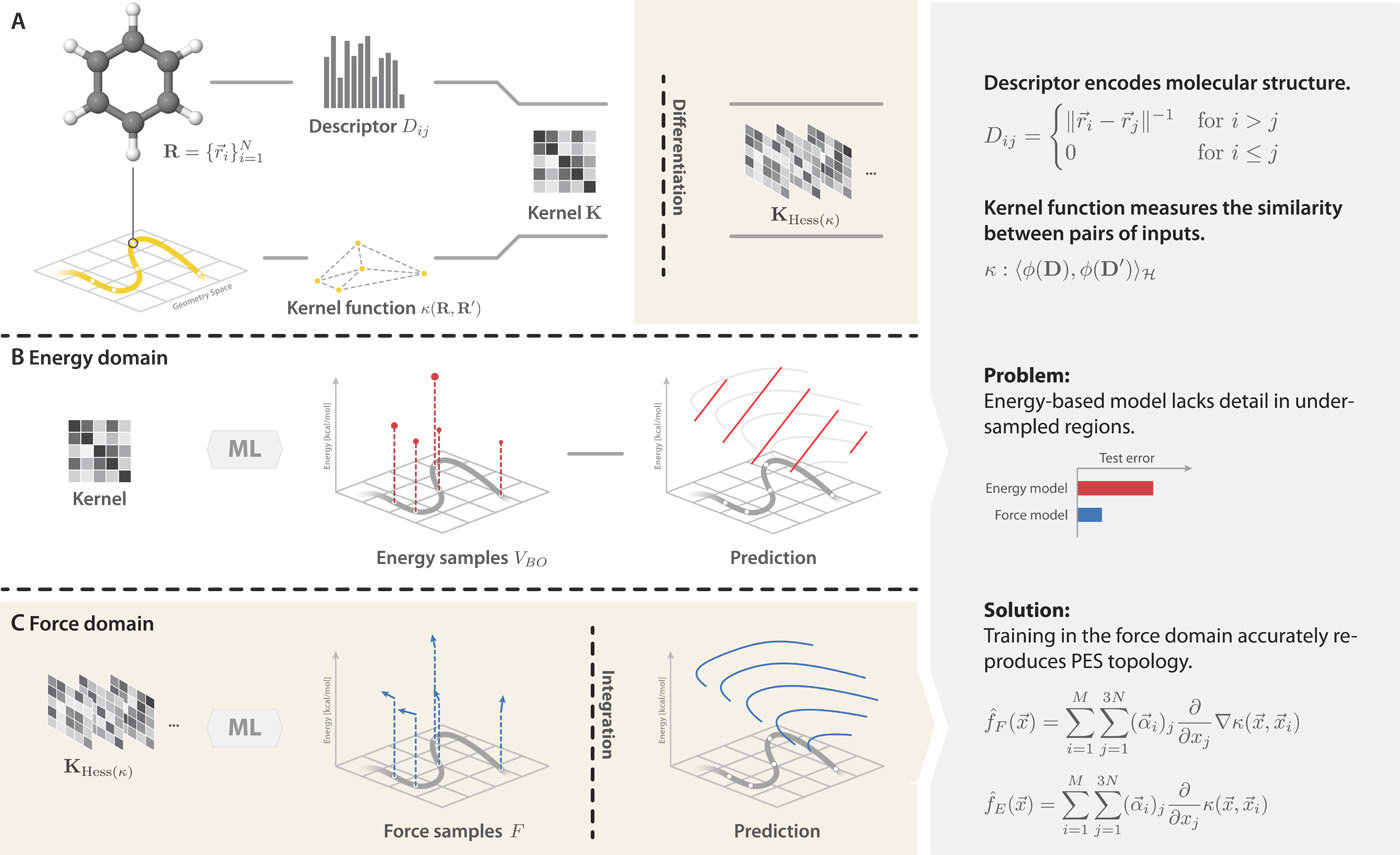
Gradient-domain machine learning (GDML)

Better interpolation

Global descriptor

Training on forces

requires 1 000 structures instead of 10 000+

Global descriptors are not size transferable

System size is still a limiting factor

Global

Fewer structures enables higher levels of theory

Local

Tons of sampling

Descriptor

Size transferable?

CCSD(T)

How can we make GDML potentials size transferable?

CCSD(T)

What we want

CCSD(T)

What we can afford

Transferability with n-body interactions

-76.31270

-76.31251

-76.31273

-228.96298

-0.00831

-0.00705

-0.00700

-228.93794

(-0.02504)

-228.96031

(-0.00267)

1 body

1+2 body

3-body

Add energy

Remove energy

All energies are in Hartrees

Many-body expansion (MBE) unlocks size transferability for expensive methods

MBE: the total energy of a system is equal to the sum of all n-body interactions

Truncate

E =

\sum E_i^{(1)}

\sum\Delta E_{ij}^{(2)}

\sum \Delta E_{ijk}^{(3)}

+ \cdots

CCSD(T)

Many-body GDML force fields incorporates more physics

Training a many-body GDML (mbGDML) potential

Sample a thousand

configurations

Calculate n-body energy (+ forces) with QC

Calculate total energies with QC

Known

E_{total} \approx \sum E_i^{(1)} + \sum\Delta E_{ij}^{(2)} + \sum \Delta E_{ijk}^{(3)}

E_{total} \approx \sum\limits^{N_{atoms}} \varepsilon_i

Known

Learned

Reproduce physical n-body energies

Approximation: atomic contributions can reproduce total energy

Sample tens of thousands of configurations

Our innovation: Many-body expansion framework accelerated with GDML

Less training data
Use higher levels of theory
Easy to parallelize

Unique opportunity with GDML accuracy and efficiency

If successful

keithgroup.github.io/mbGDML

Case study: Modeling three common solvents

Water (H2O)

Acetonitrile (MeCN)

Methanol (MeOH)

Training set

1 000 structures

(instead of 10 000+)

Sampling

n-body structures from GFN2-xTB simulations

Level of theory

MP2/def2-TZVP

ORCA v4.2.0

Useful ML force fields requires accurate relative energies

Which tetramer (4mer) has the lowest energy (i.e., global minimum)?

Isomer #1

Isomer #2

Isomer #3

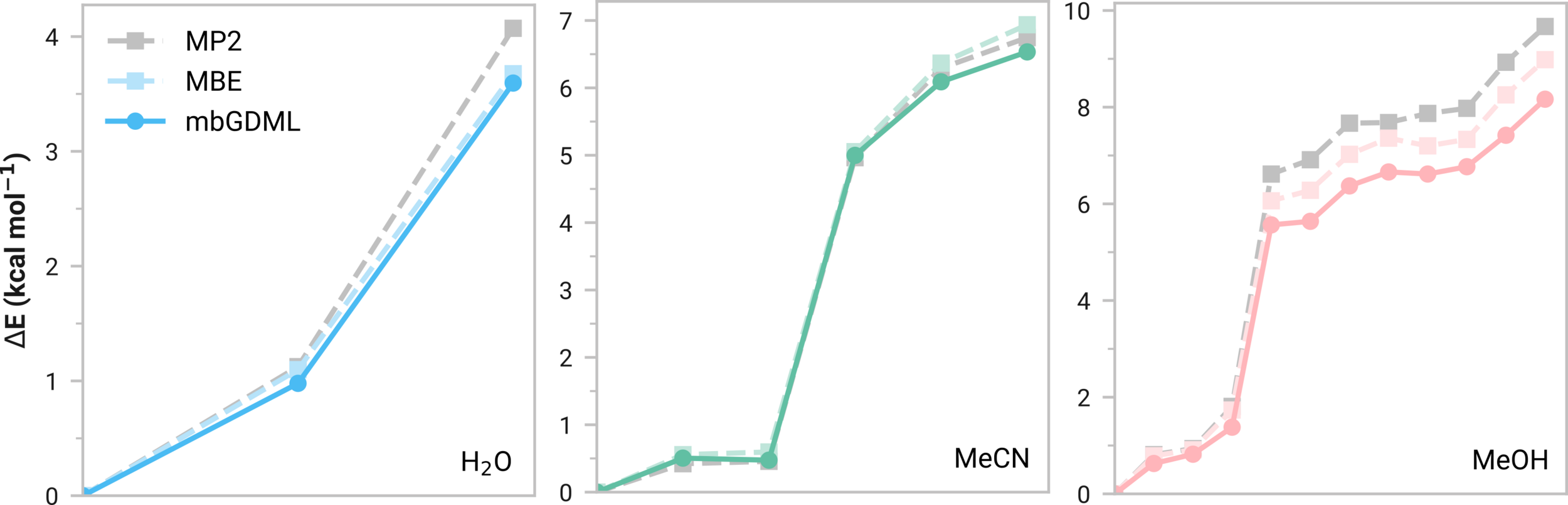
Many-body GDML accurately captures relative energies in tetramers

System	Energy Error [kcal/mol]	Force RMSE [kcal/(mol A)]
(H2O)16	4.01 (0.25)	1.12 (0.02)
(MeCN)16	0.28 (0.02)	0.35 (0.004)
(MeOH)16	5.56 (0.35)	1.79 (0.02)

mbGDML maintains accuracy on larger systems

Consistent normalized errors

Size transferable

Can we model liquids accurately?

Radial distribution function (rdf)

What we want

g(r)

Tells us if we are getting the correct liquid structure

Many-body GDML accurately captures liquid structure

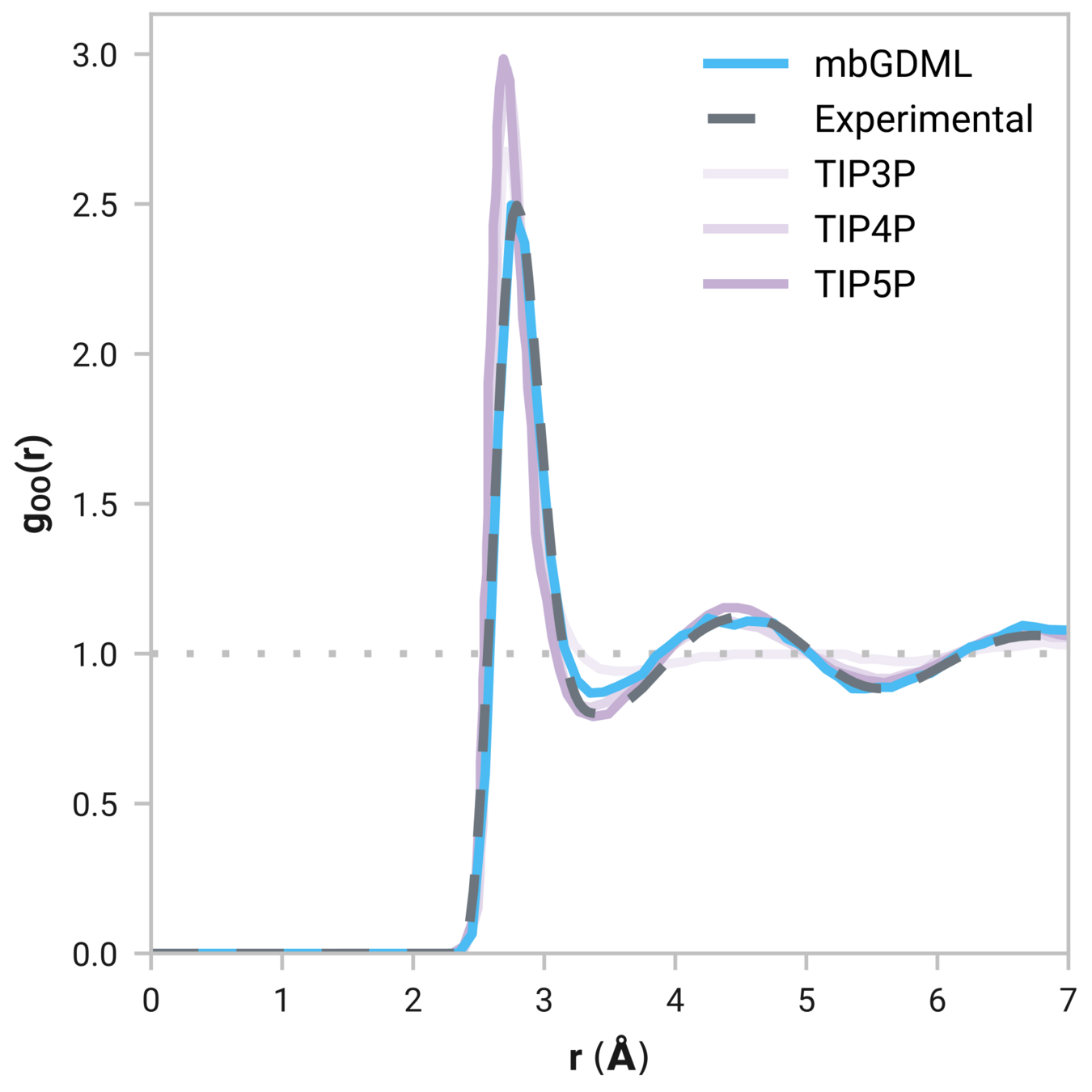
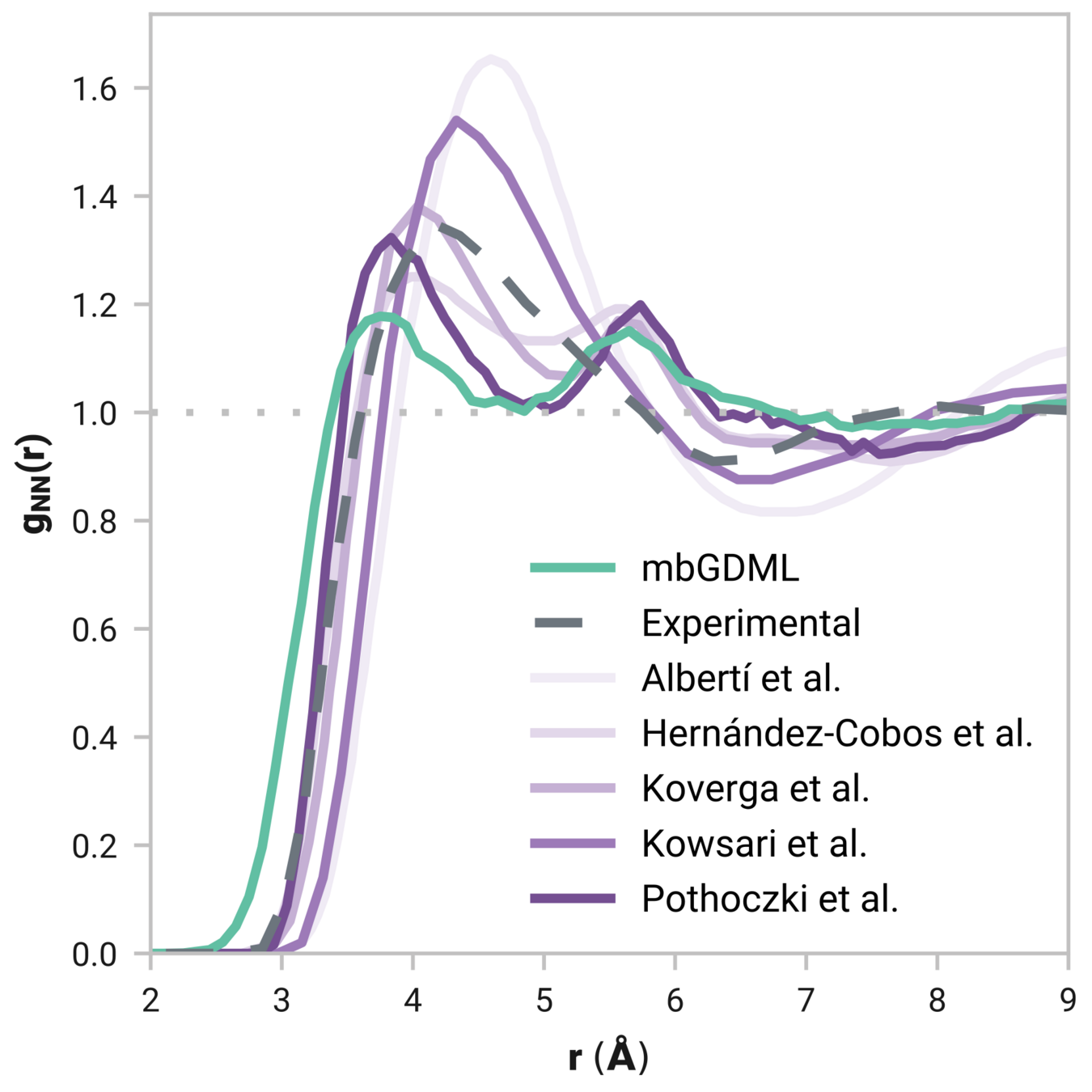
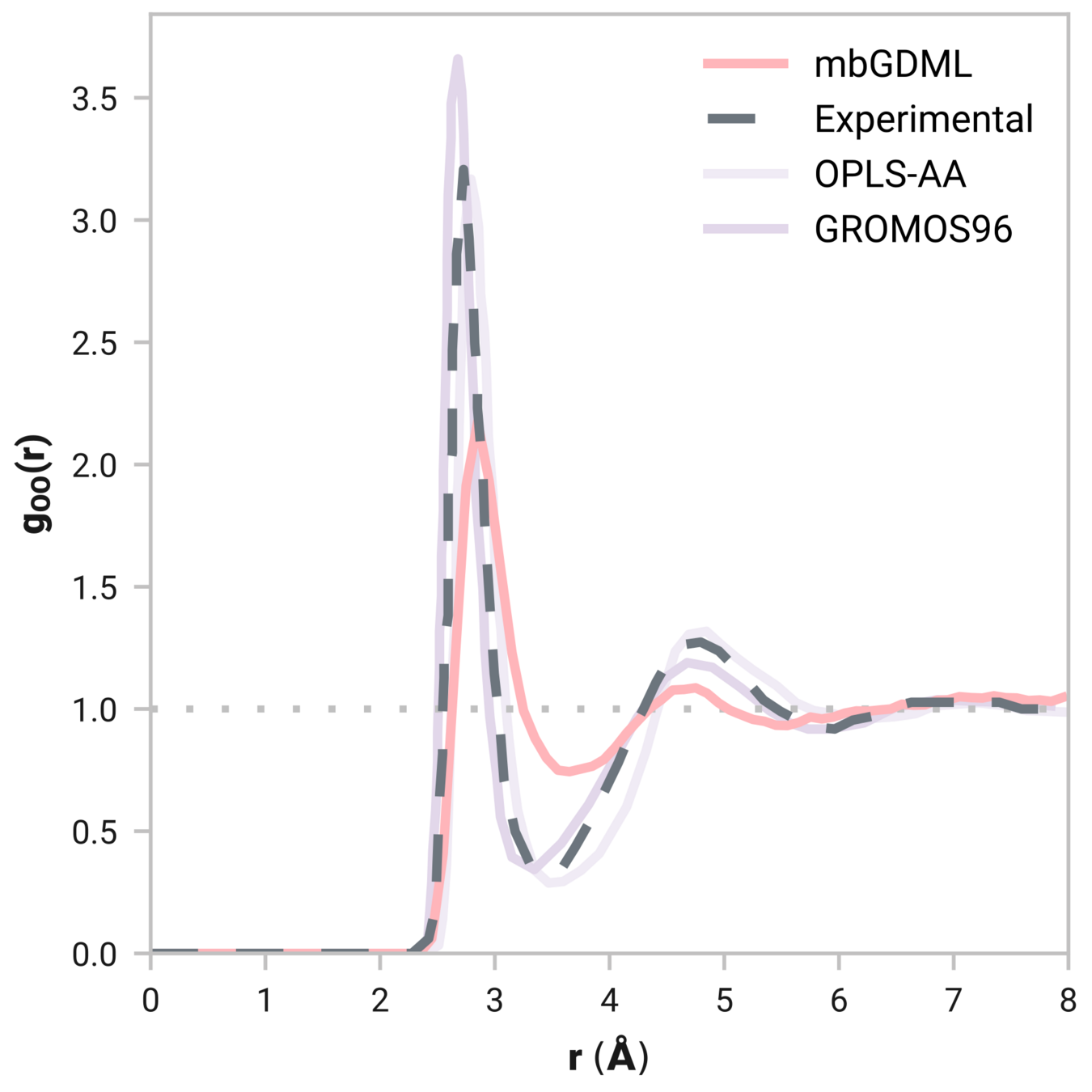
137 H2O molecules

67 MeCN molecules

61 MeOH molecules

Reminder: We have only trained on clusters with up to three molecules

Time for 10 ps MeCN simulation:

mbGDML 19 hours

\approx

MP2 23 762 years

\approx

20 ps NVT MD simulations; 1 fs time step; Berendsen thermostat at 298 K

Explicit solvent modeling without experimental data

Classical

Ab initio

mbGDML

Training

Speed

Accuracy

Scaling

Poor

Excellent