Computational Biology Seminar

(BIOSC 1630)

Sep 11, 2024

Lecture 03:
Paper 1

Announcements

  • I had to rework assignment due dates to give us more time to read the papers
  • Review assignment is due next week

Disclaimer: There are some oversimplifications and missing nuances in some physics and explanations. This is done to help students digest this material

After today, you should be able to

Describe the basic stages of drug discovery and explain the role of computational methods in modern drug design

Experimental drug discovery

Many use biochemical, in vitro, and in vivo assays to identify drug targets

This is relevant, but costly data

Reducing this cost is a high priority (and we are making good progress)

New drugs take a long time and $$$

Computer-aided drug design

Using computational power to expand our search space for novel compounds

Highly interdisciplinary:

  • Physics
  • Chemistry
  • Biology
  • Computer science

Hit identification finds small molecules that modulate target

Search through tons of molecules to find a few that show promise

Need to assess

  • Potency
  • Selectivity
  • Physicochemical properties
  • Synthesis

Two categories of drug discovery

Structure-based

  • Known target
  • Trying to find molecules that bind and modulate

Ligand-based

  • The target may be unknown
  • Have known drugs
  • Often used for lead optimization

After today, you should be able to

Identify the main types of molecular forces and explain how they relate to binding affinity and free energy.

How do we identify promising drug targets?

We want "just the right amount" of ligand binding

P + L \rightleftharpoons PL

We can model this as a reversible protein-ligand binding

Too much binding: Potential toxicity and long-term effects

Too little binding: No effect

However, it is much harder to identify drugs that bind enough

\Delta G_{PL}^\circ = - RT \ln \left( K_{eq} \right)
K_{eq} = e^{\frac{-\Delta G_{PL}^\circ}{RT}}

Thermodynamics

Kinetics

Computing either 

K_{eq}
\Delta G_{PL}^\circ

or

is sufficient for now

Computing thermodynamics is easier than kinetics

We usually start with free energy change

Kinetic calculations are numerically sensitive and require long simulations

Gibbs free energy accounts for all energy contributions

\Delta G_{bind} = \Delta H_{bind} - T\Delta S_{bind}
\Delta H_{bind}
\Delta S_{bind}

Entropy

Enthalpy

Accounts for energetic interactions

How much conformational flexibility changes

Typically, we don't calculate enthalpy and entropy separately; just straight free energy

Let's focus on enthalpy

Non-covalent interactions drive enthalpy

If the molecule connectivity does not change; intramolecular interactions are consistent

We can then focus on intermolecular (i.e., non-covalent) interactions

Intermolecular forces are just electrostatics with extra steps

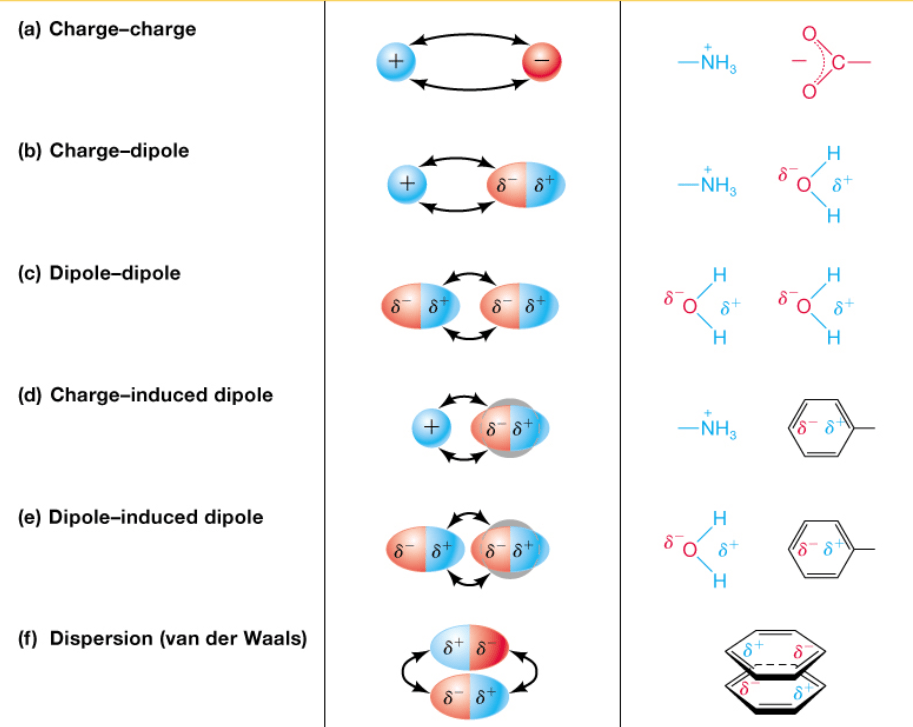
Changes in these interactions contribute to enthalpic changes

(Desolvation is another, but not important right now.)

Point charges follow Coulomb's law

Electron density

Hard spheres

\vec{F} = k \frac{q_1 q_2}{r^2} \hat{r}

Instead of modeling the wave function, we model atoms as hard spheres

Quantum particles are like charged dust clouds

Quantum particles behave like a "wave" and "particle"

Electrons are neither; they are something else

A (over) simplification is to think of electrons like a swirling, charged dust cloud

Two electron clouds with different properties will spatially distort

Thus, our electron clouds will distort based on "unequal sharing of electrons"

Here, Si and O have different electronic properties

(We call this "electronegativity")

Cannot treat spatially varying charges as points

We call these dipoles because they vary about the radius and z axis

Quadrupoles have additional variation

These contributions are called "polarization", and they are not always included because of cost

Hydrogen bonding is just electrostatics with extra steps

pi-interactions are also electrostatic with extra steps

There is an unequal distribution of electron density in rings

Edge-to-face

Displaced

Face-to-face

These non-covalent interactions dominate protein-ligand binding

After today, you should be able to

Explain basic concepts of statistical thermodynamics, including ensemble averages and the relationship between microscopic properties and macroscopic observables.

Computing differences in non-covalent interactions gives us enthalpy

Great!

Now we just need to compute these differences

\Delta G_{PL} = G_{PL} - G_{P} - G_{L}

Let's focus on the enthalpic contributions of the ligand

Remember that these are free energies in solution!

Compute all intra and intermolecular interactions

The issue is, there is more than one conformation

We can go through and compute all interactions using a force field (discussed later)

Generate conformations and compute energies

We can compute the ligand's free energy by computing the mean of all conformations

G = \sum_i G_{\text{Conf}_i}

Well, no. We have an issue.

(This collection of conformations is called an ensemble.)

Molecules do not spend equal time in each conformation

Suppose some conformations have really high energy

If we use a simple mean, then these conformations have equal weight to low energy conformations

Molecules spend more time in low-energy conformations, so they should have a larger contribution to the average

We need to compute a weighted average

So, we can compute a weighted average by

G = \sum_i w_i G_i

What is the weight for each conformation?

The most natural weighting factor is the energy

w_i = \frac{e^{-\beta E_i}}{\sum_i e^{-\beta E_i}}

This is called the Boltzmann weight

\beta = k_B T

is the Boltzmann constant

k_B

Great! I can compute a weighted average, but how do I get all configurations?

Systematic searches numerically iterate over all possible conformations

Identify important degrees of freedom

  • Angles
  • Dihedrals

Scan along each angle with a step size of a N degrees

Remove structures with high strain

Systematic searches are only possible for very small molecules

How many different conformations would we have in this molecule if we scanned only dihedrals every 45 degrees?

Systematic searches are only possible for very small molecules

8 dihedrals

1

2

3

4

5

6

7

8

8 angles

8 × 8 × 8 × 8 × 8 × 8 × 8 × 8 = 16,777,216

That's a lot of structures, and many of them will clash!

We almost never do a systematic search in practice without some precautions to combinatorics

Low-energy conformers dominate our average

w_i = \frac{e^{-\beta E_i}}{\sum_i e^{-\beta E_i}}

High energy conformations will have a small weight, so we can get close enough if we just identify low energy conformations

It's much easier to run molecular simulations to "sample" low energy geometries

For high accuracy, you still need high energy conformations

After today, you should be able to

Explain the basic principles of molecular simulations.

Molecular simulations compute an atomistic trajectory

Suppose we have 3D coordinates of atoms in our system

These atoms exert forces on each other

Using Newton's equation of motion, we can predict their velocity

Now, we move the atoms the distance they would travel in one femtosecond

Then we repeat

Then you get an trajectory of atomic positions

By running these simulations correctly, you can sample low energy conformations

Molecular simulations have difficulty capturing long-scale dynamics

Most simulations (in my experience) are on the order of 100s of ns

After today, you should be able to

Explain the basic principles of force fields.

How we compute these atomic forces is with a "force field"

Computing accurate atomic forces is paramount

Quantum mechanics is the most accurate at a steep, step computational cost

Iteratively optimize orbital shapes until you minimize energies

Many, many intensive integrals

30 atoms can take hours

Computing accurate atomic forces quickly is paramount

Instead, we use analytical expressions to approximate quantum chemical forces

Analytical functions (i.e., typical equations) are way faster to compute

Let's look at bond dissociation

H2 energies along a bond scan

What do you think the curve would look like?

Energies are computed with CISD/aug-cc-pVTZ

How to reproduce this analytically?

Do we care about all bond lengths?

No

Unless we are breaking bonds, we only care about the minimum

How to reproduce this analytically?

Harmonic centered on minimum

V = \frac{1}{2} k \left( r - r_{eq} \right)^2

Note that we shifted the minimum to be at zero

1/2 is optional

V = D_e \left( 1 - e^{-a \left( r - r_{eq} \right)} \right)^2

Morse potential better captures bond-breaking of a quantum oscillator

V = D_e \left( 1 - e^{-a \left( r - r_{eq} \right)} \right)^2

Most force fields use harmonic oscillators, why?

V = \frac{1}{2} k \left( r - r_{eq} \right)^2

Exponentials are significantly slower to calculate

Simple timing test showed Morse potentials are at least 1.5 to 2.0 times slower

Balance of cost and accuracy

Different parameters for different bonding

Systematic evaluations can develop transferable, generalized parameters

Different parameters for different bonding

Energies are computed with CISD/cc-pVTZ

Quantum systems have quantized energy levels

Aside: We have been ignoring the zero-point vibrational energy

The lowest energy of a dimer is not at the bottom of the energy function

However, this is computationally intensive to account for?

Molecules will still vibrate at 0 Kelvin (and we can never get to 0 Kelvin)

Angles

Energies are computed with CISD/cc-pVTZ

V = k \left( \theta_i - \theta_{eq} \right)^2

Torsions

Energies are computed with MP2/cc-pVTZ

V = K_\omega \left[ 1 + \cos \left( n \omega_i - \gamma_i \right) \right]

van der Waals interactions

V = 4 \varepsilon_{ij} \left[ \left( \frac{\sigma_{ij}}{r_{ij}} \right)^{12} + \left( \frac{\sigma_{ij}}{r_{ij}} \right)^{6} \right]

We use experimental data to improve our classical force fields

Even if we could, QC is not perfect

Different "level of theories" gives you different accuracy

If you fit a classical force field just to QC, you will get "okay" accuracy

We cannot run accurate QC on whole proteins, so we have to chunk it into amino acid interactions 

How do we get accurate, useable force fields?

Use experimental data

After fitting our QC data, we tune our parameters to match experimental data

Experimental Data for Protein Force Field Fitting:

  • X-ray crystallography: Atomic structures
  • NMR spectroscopy: Protein dynamics and conformations
  • Vibrational spectroscopy (IR/Raman): Bond vibrations
  • Thermodynamic data: e.g., Heat capacities, solvation energies
  • Protein-ligand binding data: Experimental affinities

This is why we have different force fields. Different labs focus on specific criteria and have opinions on what is important

After today, you should be able to

Compare and contrast Free Energy Perturbation (FEP) and Thermodynamic Integration (TI), including their advantages and limitations.

At this point, we could run molecular simulations of different states

This is a theoretically valid way, but is not practical

\Delta G_{PL} =
G_{PL}
G_{PL}
G_{L}
-
-

Binding energies are small (e.g., ~10 kcal/mol)

Absolute free energies are very large (e.g., thousands of kcal/mol)

Sampling is largely uncorrelated

What if we slowly disappear the ligand?

This has several advantages:

More relevant conformational sampling

Can run independent simulations in parallel

Focuses on taking differences with smaller numbers

This technical is generally called alchemical simulations

An alchemical parameter controls our protein-ligand interactions

\lambda = 1.0
\lambda = 0.5
\lambda = 0.0

One means interactions are normal; zero means no intermolecular interactions are on

Intramolecular interactions are left alone

What interactions are turned off?

Our non-covalent interactions:
Electrostatic and van der Waals interactions

Thermodynamic integration provides a way to compute free energy differences

\Delta F_{A \to B} = F_B - F_A = \int_0^1 \left\langle \frac{\partial U(\lambda)}{\partial \lambda} \right\rangle_\lambda d\lambda

We can to integrate over these small free energy changes 

Free energy perturbation is similar

In TI, we run a simulation with one alchemical parameter value

In FEP, we run fewer simulations but calculate the energy of other alchemical parameters at the same time

After today, you should be able to

Explain how replica exchange methods enhance sampling in molecular simulations and their application in free energy calculations.

Recall: Accurate averages require sampling of low and high energy structures

Similar to a reaction, our simulations have to overcome energetic barriers to sample conformations

For vanilla molecular simulations, all we can do is sit and wait simulations to end up in that conformation

Rare-event sampling helps accelerate this process

We artificially add energy to conformations we have seen before

This reduces the energetic barrier to get to high energy conformations

After our simulations, we can remove this bias

This is called metadynamics

Metadynamics is challenging because we have to choose a coordinate

For reactions, we can use bond lengths as coordinates

What coordinate can we use for protein and ligand conformations?

Root-mean squared deviation is a common metric

However, reducing all of these conformations to one number is a massive oversimplification

We can ramp up our temperature to decrease barriers

By cycling the temperature, we can help escape local minima

Replica-exchange has parallel simulations that randomly change temperature

EDS changes our molecule instead of temperature

Before the next class, you should

Lecture 04:
Paper 01 discussion

Lecture 03:
Paper 01 methods

Today

Next Wednesday