Computational Biology Seminar
(BIOSC 1630)
Sep 11, 2024
Lecture 03:
Paper 1
Announcements
- I had to rework assignment due dates to give us more time to read the papers
- Review assignment is due next week
Disclaimer: There are some oversimplifications and missing nuances in some physics and explanations. This is done to help students digest this material
After today, you should be able to
Describe the basic stages of drug discovery and explain the role of computational methods in modern drug design
Experimental drug discovery
Many use biochemical, in vitro, and in vivo assays to identify drug targets
This is relevant, but costly data
Reducing this cost is a high priority (and we are making good progress)
New drugs take a long time and $$$
Computer-aided drug design
Using computational power to expand our search space for novel compounds
Highly interdisciplinary:
- Physics
- Chemistry
- Biology
- Computer science
Hit identification finds small molecules that modulate target
Search through tons of molecules to find a few that show promise
Need to assess
- Potency
- Selectivity
- Physicochemical properties
- Synthesis
Two categories of drug discovery
Structure-based
- Known target
- Trying to find molecules that bind and modulate
Ligand-based
- The target may be unknown
- Have known drugs
- Often used for lead optimization
After today, you should be able to
Identify the main types of molecular forces and explain how they relate to binding affinity and free energy.
How do we identify promising drug targets?
We want "just the right amount" of ligand binding
P + L \rightleftharpoons PL
We can model this as a reversible protein-ligand binding
Too much binding: Potential toxicity and long-term effects
Too little binding: No effect
However, it is much harder to identify drugs that bind enough
\Delta G_{PL}^\circ = - RT \ln \left( K_{eq} \right)
K_{eq} = e^{\frac{-\Delta G_{PL}^\circ}{RT}}
Thermodynamics
Kinetics
Computing either
K_{eq}
\Delta G_{PL}^\circ
or
is sufficient for now
Computing thermodynamics is easier than kinetics
We usually start with free energy change
Kinetic calculations are numerically sensitive and require long simulations
Gibbs free energy accounts for all energy contributions
\Delta G_{bind} = \Delta H_{bind} - T\Delta S_{bind}
\Delta H_{bind}
\Delta S_{bind}
Entropy
Enthalpy
Accounts for energetic interactions
How much conformational flexibility changes
Typically, we don't calculate enthalpy and entropy separately; just straight free energy
Let's focus on enthalpy
Non-covalent interactions drive enthalpy
If the molecule connectivity does not change; intramolecular interactions are consistent
We can then focus on intermolecular (i.e., non-covalent) interactions
Intermolecular forces are just electrostatics with extra steps
Changes in these interactions contribute to enthalpic changes
(Desolvation is another, but not important right now.)
Point charges follow Coulomb's law
Electron density
Hard spheres
\vec{F} = k \frac{q_1 q_2}{r^2} \hat{r}
Instead of modeling the wave function, we model atoms as hard spheres
Quantum particles are like charged dust clouds
Quantum particles behave like a "wave" and "particle"
Electrons are neither; they are something else
A (over) simplification is to think of electrons like a swirling, charged dust cloud
Two electron clouds with different properties will spatially distort
Thus, our electron clouds will distort based on "unequal sharing of electrons"
Here, Si and O have different electronic properties
(We call this "electronegativity")
Cannot treat spatially varying charges as points
We call these dipoles because they vary about the radius and z axis
Quadrupoles have additional variation
These contributions are called "polarization", and they are not always included because of cost
Hydrogen bonding is just electrostatics with extra steps
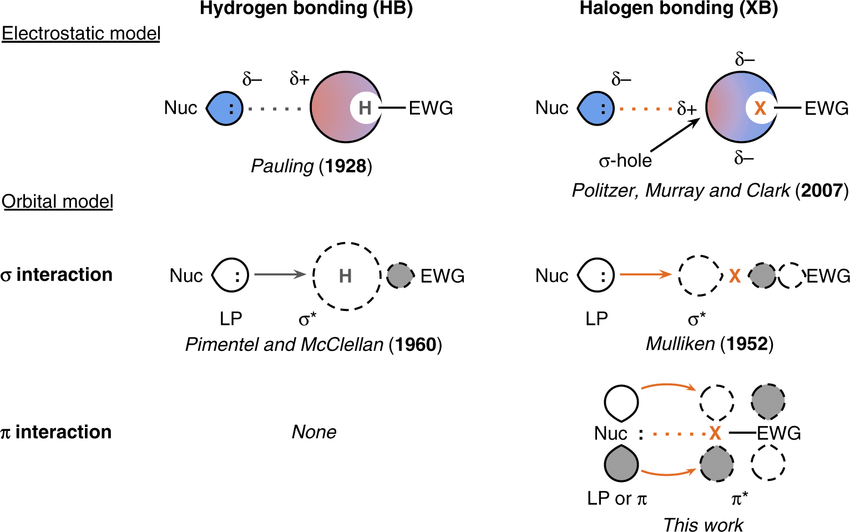
pi-interactions are also electrostatic with extra steps
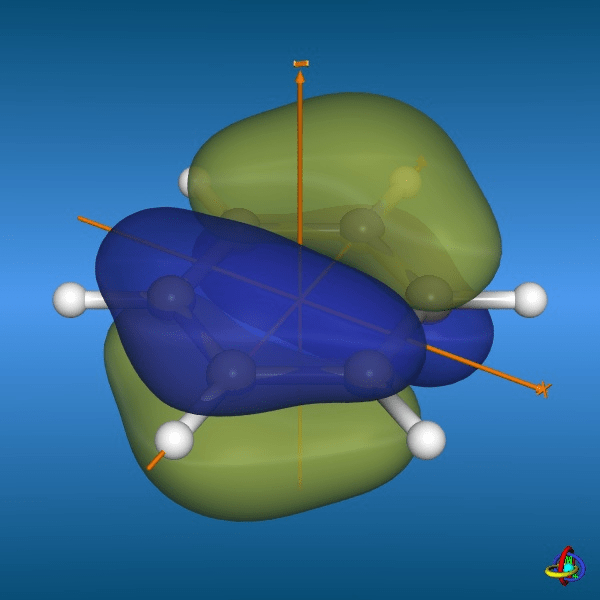
There is an unequal distribution of electron density in rings
Edge-to-face
Displaced
Face-to-face
These non-covalent interactions dominate protein-ligand binding
After today, you should be able to
Explain basic concepts of statistical thermodynamics, including ensemble averages and the relationship between microscopic properties and macroscopic observables.
Computing differences in non-covalent interactions gives us enthalpy
Great!
Now we just need to compute these differences
\Delta G_{PL} = G_{PL} - G_{P} - G_{L}
Let's focus on the enthalpic contributions of the ligand
Remember that these are free energies in solution!
Compute all intra and intermolecular interactions
The issue is, there is more than one conformation
We can go through and compute all interactions using a force field (discussed later)
Generate conformations and compute energies
We can compute the ligand's free energy by computing the mean of all conformations
G = \sum_i G_{\text{Conf}_i}
Well, no. We have an issue.
(This collection of conformations is called an ensemble.)
Molecules do not spend equal time in each conformation
Suppose some conformations have really high energy
If we use a simple mean, then these conformations have equal weight to low energy conformations
Molecules spend more time in low-energy conformations, so they should have a larger contribution to the average
We need to compute a weighted average
So, we can compute a weighted average by
G = \sum_i w_i G_i
What is the weight for each conformation?
The most natural weighting factor is the energy
w_i = \frac{e^{-\beta E_i}}{\sum_i e^{-\beta E_i}}
This is called the Boltzmann weight
\beta = k_B T
is the Boltzmann constant
k_B
Great! I can compute a weighted average, but how do I get all configurations?
Systematic searches numerically iterate over all possible conformations
Identify important degrees of freedom
- Angles
- Dihedrals
Scan along each angle with a step size of a N degrees
Remove structures with high strain
Systematic searches are only possible for very small molecules
How many different conformations would we have in this molecule if we scanned only dihedrals every 45 degrees?
Systematic searches are only possible for very small molecules
8 dihedrals
1
2
3
4
5
6
7
8
8 angles
8 × 8 × 8 × 8 × 8 × 8 × 8 × 8 = 16,777,216
That's a lot of structures, and many of them will clash!
We almost never do a systematic search in practice without some precautions to combinatorics
Low-energy conformers dominate our average
w_i = \frac{e^{-\beta E_i}}{\sum_i e^{-\beta E_i}}
High energy conformations will have a small weight, so we can get close enough if we just identify low energy conformations
It's much easier to run molecular simulations to "sample" low energy geometries
For high accuracy, you still need high energy conformations
After today, you should be able to
Explain the basic principles of molecular simulations.
Molecular simulations compute an atomistic trajectory
Suppose we have 3D coordinates of atoms in our system
These atoms exert forces on each other
Using Newton's equation of motion, we can predict their velocity
Now, we move the atoms the distance they would travel in one femtosecond
Then we repeat
Then you get an trajectory of atomic positions
By running these simulations correctly, you can sample low energy conformations
Molecular simulations have difficulty capturing long-scale dynamics
Most simulations (in my experience) are on the order of 100s of ns
After today, you should be able to
Explain the basic principles of force fields.
How we compute these atomic forces is with a "force field"
Computing accurate atomic forces is paramount
Quantum mechanics is the most accurate at a steep, step computational cost
Iteratively optimize orbital shapes until you minimize energies
Many, many intensive integrals
30 atoms can take hours
Computing accurate atomic forces quickly is paramount
Instead, we use analytical expressions to approximate quantum chemical forces
Analytical functions (i.e., typical equations) are way faster to compute
Let's look at bond dissociation
H2 energies along a bond scan
What do you think the curve would look like?
Energies are computed with CISD/aug-cc-pVTZ
How to reproduce this analytically?
Do we care about all bond lengths?
No
Unless we are breaking bonds, we only care about the minimum
How to reproduce this analytically?
Harmonic centered on minimum
V = \frac{1}{2} k \left( r - r_{eq} \right)^2
Note that we shifted the minimum to be at zero
1/2 is optional
V = D_e \left( 1 - e^{-a \left( r - r_{eq} \right)} \right)^2
Morse potential better captures bond-breaking of a quantum oscillator
V = D_e \left( 1 - e^{-a \left( r - r_{eq} \right)} \right)^2
Most force fields use harmonic oscillators, why?
V = \frac{1}{2} k \left( r - r_{eq} \right)^2
Exponentials are significantly slower to calculate
Simple timing test showed Morse potentials are at least 1.5 to 2.0 times slower
Balance of cost and accuracy
Different parameters for different bonding
Systematic evaluations can develop transferable, generalized parameters
Different parameters for different bonding
Energies are computed with CISD/cc-pVTZ
Quantum systems have quantized energy levels
Aside: We have been ignoring the zero-point vibrational energy
The lowest energy of a dimer is not at the bottom of the energy function
However, this is computationally intensive to account for?
Molecules will still vibrate at 0 Kelvin (and we can never get to 0 Kelvin)
Angles
Energies are computed with CISD/cc-pVTZ
V = k \left( \theta_i - \theta_{eq} \right)^2
Torsions
Energies are computed with MP2/cc-pVTZ
V = K_\omega \left[ 1 + \cos \left( n \omega_i - \gamma_i \right) \right]
van der Waals interactions
V = 4 \varepsilon_{ij} \left[ \left( \frac{\sigma_{ij}}{r_{ij}} \right)^{12} + \left( \frac{\sigma_{ij}}{r_{ij}} \right)^{6} \right]
We use experimental data to improve our classical force fields
Even if we could, QC is not perfect
Different "level of theories" gives you different accuracy
If you fit a classical force field just to QC, you will get "okay" accuracy
We cannot run accurate QC on whole proteins, so we have to chunk it into amino acid interactions
How do we get accurate, useable force fields?
Use experimental data
After fitting our QC data, we tune our parameters to match experimental data
Experimental Data for Protein Force Field Fitting:
- X-ray crystallography: Atomic structures
- NMR spectroscopy: Protein dynamics and conformations
- Vibrational spectroscopy (IR/Raman): Bond vibrations
- Thermodynamic data: e.g., Heat capacities, solvation energies
- Protein-ligand binding data: Experimental affinities
This is why we have different force fields. Different labs focus on specific criteria and have opinions on what is important
After today, you should be able to
Compare and contrast Free Energy Perturbation (FEP) and Thermodynamic Integration (TI), including their advantages and limitations.
At this point, we could run molecular simulations of different states
This is a theoretically valid way, but is not practical
\Delta G_{PL} =
G_{PL}
G_{PL}
G_{L}
-
-
Binding energies are small (e.g., ~10 kcal/mol)
Absolute free energies are very large (e.g., thousands of kcal/mol)
Sampling is largely uncorrelated
What if we slowly disappear the ligand?
This has several advantages:
More relevant conformational sampling
Can run independent simulations in parallel
Focuses on taking differences with smaller numbers
This technical is generally called alchemical simulations
An alchemical parameter controls our protein-ligand interactions
\lambda = 1.0
\lambda = 0.5
\lambda = 0.0
One means interactions are normal; zero means no intermolecular interactions are on
Intramolecular interactions are left alone
What interactions are turned off?
Our non-covalent interactions:
Electrostatic and van der Waals interactions
Thermodynamic integration provides a way to compute free energy differences
\Delta F_{A \to B} = F_B - F_A = \int_0^1 \left\langle \frac{\partial U(\lambda)}{\partial \lambda} \right\rangle_\lambda d\lambda
We can to integrate over these small free energy changes
Free energy perturbation is similar
In TI, we run a simulation with one alchemical parameter value
In FEP, we run fewer simulations but calculate the energy of other alchemical parameters at the same time
After today, you should be able to
Explain how replica exchange methods enhance sampling in molecular simulations and their application in free energy calculations.
Recall: Accurate averages require sampling of low and high energy structures
Similar to a reaction, our simulations have to overcome energetic barriers to sample conformations
For vanilla molecular simulations, all we can do is sit and wait simulations to end up in that conformation
Rare-event sampling helps accelerate this process
We artificially add energy to conformations we have seen before
This reduces the energetic barrier to get to high energy conformations
After our simulations, we can remove this bias
This is called metadynamics
Metadynamics is challenging because we have to choose a coordinate
For reactions, we can use bond lengths as coordinates
What coordinate can we use for protein and ligand conformations?
Root-mean squared deviation is a common metric
However, reducing all of these conformations to one number is a massive oversimplification
We can ramp up our temperature to decrease barriers
By cycling the temperature, we can help escape local minima
Replica-exchange has parallel simulations that randomly change temperature
EDS changes our molecule instead of temperature
Before the next class, you should
Lecture 04:
Paper 01 discussion
Lecture 03:
Paper 01 methods
Today
Next Wednesday
BIOSC 1630: Lecture 03
By aalexmmaldonado
