Greedy
&
二分搜
&
分治
演算法小社 [5] 、[6]
by 鹽亞倫
索引(可以點)

我也不知道今天可以上多少於是決定和下週用同個簡報
題外話:
請學弟妹將你的 codeforces handle 私訊給講師,我們要把你們加入建北電資的 CF group 內
Greedy
貪婪
貪婪是什麼?
- 姜姜一個女朋友還不夠,還要追別的女生
- Brine 一科校隊了還想要再拿一科
Want more and better!
蛤?
不拿白不拿
直接給一個例子:
給你很多杯飲料,有的喝下去會精神百倍,增加你的能量值(蛤?),而有的喝下去會讓你想吐,倒扣能量值。
現在給你每次給你一杯飲料和他能帶給你的能量\(E_i\) \(( -10^5 < E_i < 10^5)\)
問你要不要喝
你要怎麼選擇才能讓能量最高?
你會想說:阿我就只喝會增加能量的就好了啊!
所以貪婪到底是什麼?
我每一次只選擇當前看起來比較好的那個做法
而我希望這個作法可以讓最後的結果最好!
But~
使用前要想想,這個題目貪婪確定會是對的嗎?
以剛剛飲料為例,只選擇能量是正的
重要事項:想到貪婪作法之後,要記得證明他是對的
直接講定義大概聽不太懂,因此直接帶幾題貪婪的例題
想到 Greedy 做法之後很重要的步驟:
如何證明是對的?
通常會用兩個做法:
- 數學歸納法
- 反證法
(證明照著greedy做,不會有更好的解你找不到)


範例時間 1
TIOJ 1072 誰先晚餐
寫Greedy :
- 想到一個做法
- 驗證那個做法
所以有人有想到作法嗎?
先想想題目要求的那個時間怎麼算?
答案 \(= \displaystyle \max_{1\le i \le n} ( \)第 \(i\) 人上菜時間 \(+\, i\) 吃飯時間\()\)
先做吃飯快的?慢的?要做比較久的?做比較快的?
按照吃東西的時間排序,比較慢的先吃
為什麼這是對的?
假設兩個人a、b
做菜時間為\(C_a\)、\(C_b\)
吃飯時間為 \(E_a\)、\(E_b\),且 a 吃比較慢
這時候可以發現
a 先吃
b 先吃
b 耗時
a 耗時
\(C_a + C_b + E_a\)
\(C_b + E_b\)
\(C_b + C_a + E_b\)
\(C_a + E_a\)
所以,較慢的人先吃的最後時間一定比較快先吃時間還要少
結論:用排序的!
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <climits>
#include <bitset>
#define All(x) begin(x),end(x)
#define ll long long int
#define debug(x) cerr<<#x<<" = "<<(x)<<endl
#define _ ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
int main() {_
int n;
while (cin >> n && n) { // 迴圈到n不為0
vector<pair<int, int>> arr;
for (int i=0; i<n; ++i) {
int c,e;
cin >> c >> e;
arr.push_back(make_pair(e, c));
}
sort(arr.begin(), arr.end(), greater<pair<int, int>>()); // pair 的 greater 會先比較第一項大小再比較第二項
ll curTime = 0; // 廚師煮飯到現在的時間
ll maxTime = 0;
for (int i=0; i<n; ++i) {
curTime = curTime + arr[i].second;
maxTime = max(maxTime, curTime + arr[i].first); // curTime + arr[i].first是第i人離開的時間
}
cout << maxTime << endl;
}
return 0;
}
AC code
範例時間 2
TIOJ 1861 蘿莉切割問題
原題序很噁心請忽視
和諧版題序:
- 給你一塊東西,你要把它切成 K 塊,每塊有指定的大小。
- 而將一塊大小為 \(w_i \) 東西切分為兩塊的代價是\(w_i\)
- 問要怎麼切,才可以讓代價最小?
- 提示:
- 正確的做法其實不是從切割下手
要怎麼做?
換個思考方式
改成把切塊的東西合併!
代價為兩個合併的東西大小相加
有想到要怎麼greedy嗎?(再給你們想30秒)
正確做法:
每次選兩個最小的合併!
How To 實作?
還記得上禮拜的priority_queue嗎
怎麼(不嚴謹)證明
假設這個合併順序是我們greedy的做法
a
b
a + b
a + b + c
c
也就是說 a , b < c
假設我們合併時不按照greedy的順序,舉例,我們把a和c互換
再去計算我們花費的代價,你會發現無論ac互換或是bc順序互換,greedy的做法都不會比較差
計算過程我就爛的寫了
然後,你可以說明一件事
任何一棵需要被你合併的樹
如果將較深的節點先以最佳解做完之後,都會變成剛剛的狀況
所以就可以用數學歸納法證明了
聽到這邊覺得聽不太懂很正常
因為greedy做法的證明有時候的確需要較複雜的數學。
可以嘗試看看用心感受是不是對的
因此在比賽當中常常更需要的是直覺,覺得可以用greedy寫,就試試看吧,吃WA了就再說
AC code:
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
#define ll long long
#define _ ios::sync_with_stdio(false);cin.tie(0);
using namespace std;
signed main() {_
ll n;
while (cin>>n) {
priority_queue<ll, vector<ll>, greater<ll> > pq;
for (ll i=0; i<n; i++) {
ll temp;
cin>>temp;
pq.push(temp);
}
ll sum=0;
ll a,b;
while (pq.size() > 1) {
a = pq.top();
pq.pop();
b = pq.top();
pq.pop();
sum += a+b;
pq.push(a+b);
}
cout << sum << endl;
}
return 0;
}
記得開long long!!!
偷偷教一個爛招式,如果你寫完int結果想要改成long long,你可以
#define int long long
但是int main()要記得改成signed main()
練習時間
再來看看一題超級通靈的題目
NPSC 2021 pG 陣列刪除
(TIOJ 2271)
哈哈自己加油吧等等下課前再公佈答案
(我絕對不會跟你說下一頁就有詳解)
hint:
ANS:
答案為陣列最小的 n/2 個元素的和
sort過去就好
蛤這麼簡單????
proof:
- 總花費這樣一定是最小
- 但你怎麼肯定我一定有辦法用前 n/2 個最小的東西讓整個陣列消失?
如果 紅球代表陣列中值較小的元素 白球為較大的
可以發覺無論怎麼排,消失過哪些東西,一定有一個紅球和白球相臨!
因此一定可以用紅球把白球消失掉!
AC code
#include <bits/stdc++.h>
using namespace std;
#define AI(x) begin(x),end(x)
#define ll long long
#define endl '\n'
#define _ ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
signed main() {_
int n;
cin >> n;
vector<int> arr(n);
for (auto &i : arr) cin >> i;
sort(AI(arr));
ll ans = 0;
for (int i = 0; i < n/2; ++i) {
ans += arr[i];
}
cout << ans << endl;
return 0;
}
反悔貪婪
聽起來好渣
先做再說,後果等等再處理
給你一個數列,可以從左至右取數字,問在
過程中數字和不小於零的情況下,最多可以
拿取幾個數字?
| 4 | -4 | 1 | -3 | 1 | -3 |
|---|
總和:
4
0
1
-2 (+4) = 2
3
0
A:5個
作法:
照順序看,一開始通通都選
等到發覺新的數字\(a_i\)加進總和會 \(<0\) 的時候,就放棄一個數字
放棄哪一個勒?
已選擇的數字中 & 新數字中最小的那一個
證明就留給各位摟
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
int main(){
priority_queue<long long,vector<long long>,greater<long long>> pq;
//pq維護代價最大的藥水
int n;
cin>>n;
long long hp = 0;
long long cnt = 0;
while(n--){
int k;
cin>>k;
hp+=k;
cnt++;
pq.push(k);
while(hp<0){//生命少於0 開始反悔
cnt--;
hp-=pq.top();
pq.pop();
}
}
cout<<cnt<<endl;
}實作,用pq!
更多題目:
提示:分狀況! 詳解點我
我有照難度排列你們就greedy的往下寫吧
我錢還夠的話會繼續給獎品
Enumeration
枚舉
電腦解決有什麼難,不就暴力窮舉就好嗎
你,真的知道怎麼窮舉嗎
什麼是窮舉
當一個問題,我很難直接找出答案
但是答案是有限個,而且我有辦法判斷一個答案是不是對的
那我就把所有可能的答案一一列出來看看對不對
aka會考選擇題的答題技巧
來舉個栗子(x)雞蛋(o)
阿蘇很喜歡在雞蛋裡面挑骨頭
因此他常常會買一堆雞蛋回家,也因此他常常會發現有趣的蛋蛋,別人給他一個綽號叫做蛋王
有一天,阿蘇發現了一顆有趣的雞蛋,出其不意地硬。
這時候阿蘇不經開始思索
這顆蛋到底有多硬呢?
他整日廢寢忘食,不吃不合,半夜騎車到淡水找人emo
但還是想不出要怎麼檢查這顆蛋的硬度
終於... 他撐不下去了... 爬到屋頂上... 眺望遠方... 深吸一口氣......
把蛋一口氣丟了下去~
“ㄟ~這顆雞蛋沒有破誒”
這時候他靈光一閃
雞蛋的硬度可以用從幾樓丟才會破來代表
跑去一棟更高的大樓,開始丟雞蛋
於是,阿蘇就從較低樓層一路往上
看看雞蛋要從幾樓丟下去才不會破!
丟下去之後,阿蘇突然發覺
這就是一種窮舉方式
我沒辦法直接得知丟雞蛋的硬度
但是我可以透過嘗試所有的樓層
來檢查雞蛋會不會破
不過或許你會發現,要是這顆雞蛋超級硬,一直都不破
一層一層丟,你要丟很多次雞蛋
因此等等會想想其他更好的作法
還有什麼窮舉?
遞迴那邊有講到的
窮舉排列樹
Binary Search
二分搜
先來玩個國(ㄐㄧㄢˋ)小(ㄓㄨㄥ)生遊戲
我心中想一個 1 ~ 100 的數字給你們猜
但我只會跟你們說你們猜太大或太小
很多人應該都知道怎麼猜可以最快猜中吧
my num: 41
1
100
your guess:
50
25
37
就這樣一直砍半檢查中點!
這個技巧我們就叫做二分搜!
二分搜每一次會把東西砍成一半
因此時間複雜度為 \( \mathcal O(\log n)\)
是一個非常好用的搜尋方式
所以什麼樣的東西可以二分搜呢?
要有單調性!
蛤?供三小
這是一個01陣列
0000000000111111111111111111
假設我今天要找到第一個 0 和 1 的交界,要怎麼做?
以剛剛二分搜的想法,先檢查中間那一格是0還是1
如果中間是1,我們可以知道右邊的都不用看了(一定是1)
如果中間是0,我們可以知道左邊的都不用看了(一定是0)
101011111000111001010
但如果長這樣呢?
我中間切下去的是0,但我放棄左邊的話
第一的01交界處就找不到了!
所以,長得像是這樣的東西,我們稱之為有單調性,可以二分搜
0000000000111111111111111111
101011111000111001010
1111111111111111000000000000
而長這樣的東西,則沒有單調性,不可以二分搜
我們可以發現,如果我們把猜數字太大的結果視為1,太小視為0,那其實就是上面有單調性的陣列,而我心中的數字就是那個01的交點!
- 也就是説,能夠二分搜時,總是會有一個函式 check(x) 只回傳 0 或 1
- 而此函數具有單調性:存在一個分界,使得以上皆回傳 1,以下皆回傳 0
- 我們的目標是尋找分界處
二分搜是不是聽起來很簡單~
來就來寫寫看吧~
這題是互動題喔!
好,這時候你心中一定滿頭問號
二分搜看起來是很簡單沒有錯,啊可是我不會寫誒

Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky.
— Donald Knuth
二分搜其實超級多人會寫錯!
以下提供兩種寫法
- 左閉右閉
注意,以下 \(l\) 代表二分搜的左界
\(r\) 代表二分搜的右界
int binery_search(int l, int r) {
while (l < r) { // 注意!
int mid = (l + r) / 2; // 求中點
if (check(mid) == 1) {
r = mid; // 注意!
} else {
l = mid + 1; // 注意!
}
}
return l;
}l和r維護「可能是 1 的區間」,搜尋第一個1的位置

如果 mid 為1
讓 r 變成 mid
(mid +1已經不會為答案了)
如果 mid 為0
讓 \(l\) 變成 mid + 1
(mid 已經不會為答案了)
最後的結果:
\(l\) 會是第一個1!
2. 左閉右開
- 維護「一個 0 + 可能是 1 的區間」
- \(l\)的值會是0,\(r\)會是1

int binery_search(int l, int r) {
while (r - l > 1) { // 注意!
int mid = (l + r) / 2; // 求中點
if (check(mid) == 1) {
r = mid; // 注意!
} else {
l = mid; // 注意!
}
}
return l;
}如果 mid 為1
讓 r 變成 mid
(mid +1已經不會為答案了)
如果 mid 為0
讓 \(l\) 變成 mid
(我要維護至少一個0)
最後的結果:
\(l\) 會是最後一個0!
兩種做法各有支持者
選哪個都可以
重點是:
要知道自己在寫哪一個!
不要寫錯!
最好可以直接背起來
這題的 AC code 的拉 (點我) (我用左閉右閉)
#include <iostream>
#include "lib1044.h"
#define ll long long int
#define _ ios::sync_with_stdio(false);cin.tie(0);
using namespace std;
int main() {_
int n = Initialize();
int l = 1; int r = n;
int mid = (l+r)/2;
while (l < r) {
mid = (l+r)/2;
if (Guess(mid)){
r = mid;
}else{
l = mid + 1;
}
}
Report(l);
return 0;
}
對答案二分搜
你以為二分搜只有猜數字那麼簡單而已嗎?
回想看看剛剛的丟雞蛋
假設今天你有 10 次丟雞蛋的機會,有沒有辦法告訴我在 1 ~ 500 樓之中
從哪一層開始丟會破掉?
我們可以發現
樓層數量 vs 雞蛋會不會破
有單調性!!!
因此我們可以對樓層(答案)二分搜
再去檢查某一個樓層會不會破,來做為我們二分搜的標準!
還是聽不懂?
來看個題目:
ZJ h084 牆上海報 (APCS 2022 1月)
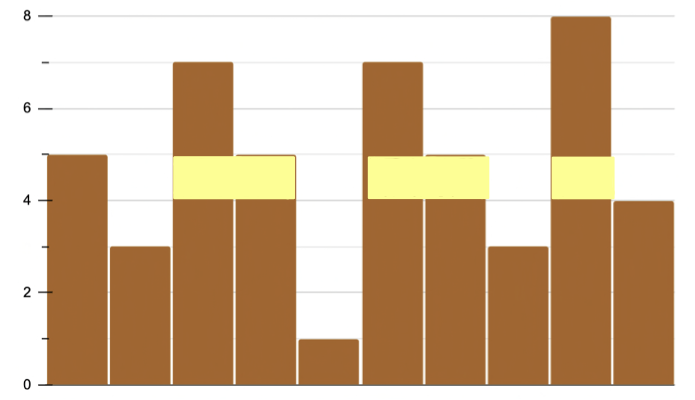
給你一面牆和很多張海報,牆由多塊不同高度木板拼起來
每張海報有寬度 w[i]
問最高可以貼多高?
注意事項:每張海報要一樣高,且按照順序貼
要怎麼做勒?
先來想窮舉
從最高的開始貼,看看什麼時候才可以貼成功?

請原諒我用excel做圖
海報: 1, 3, 2
X
X
X
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 2e5 + 5;
const int KSIZ = 5005;
const int INF = 1e9;
int n, k;
int h[SIZE], w[KSIZ];
bool check (int x) {
int pos = 1, len = 0;
for (int i = 1; i <= n; i++) {
if (h[i] >= x) len++;
else len = 0;
if (len == w[pos]) {
pos++;
len = 0;
}
if (pos > k) return 1;
}
return 0;
}
int main() {
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> h[i];
for (int i = 1; i <= k; i++) cin >> w[i];
int maxheight = 0;
for (int &i : h) maxheight = max(maxheight, i);
for (int i = maxheight; i >= 0; i--) { // 窮舉每個高度
if (check(i)) { // 檢查能不能貼海報
cout << i << endl;
break;
}
}
}
暴力窮舉的TLE code


h到1e9
O(n h)太慢了
再觀察?
我們可以發現幾件事情
- 高度越高,越不可能達成
- 假設有一個高度可以達成,比他矮的都可以!
對高度二分搜!!!
蛤?
直接來看看程式怎麼寫
高度和能不能達成有單調性!
#include <bits/stdc++.h>
using namespace std;
const int SIZE = 2e5 + 5;
const int KSIZ = 5005;
const int INF = 1e9+5;
int n, k;
int h[SIZE], w[KSIZ];
bool ok (int x) {
int pos = 1, len = 0;
for (int i = 1; i <= n; i++) {
if (h[i] >= x) len++;
else len = 0;
if (len == w[pos]) {
pos++;
len = 0;
}
if (pos > k) return 1;
}
return 0;
}
int main() {
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> h[i];
for (int i = 1; i <= k; i++) cin >> w[i];
int l = 1, r = INF;
while (l < r) {
int mid = (l + r) / 2;
if (!ok (mid)) r = mid;
else l = mid + 1;
}
cout << l - 1 << '\n';
}
複雜度 O(n log h),AC
給 \(N\) 個電信公司需要服務的據點的座標 \(x_i\)
並且最多可以架設 \(K\) 個基地台在任一座標位置
每個基地台服務的半徑範圍皆一樣
求半徑至少為多少可以覆蓋所有據點?
\(1 \le K<N \le 50000, \ 0 \le x_i \le 10^9\)
有點難?
換個問題
換一個問題
給 \(N\) 個電信公司需要服務的據點的座標 \(x_i\)
並且最多可以架設 \(K\) 個基地台在任一座標位置
每個基地台服務的半徑範圍皆一樣
給定一個半徑,問你能不能覆蓋到全部的基地台
how
每次都把半徑的最左邊卡在目前最左邊的基地台,被半徑覆蓋住的就忽略它,做到沒有基地台為止
這就是check函數!
換一個問題ㄉcode
每次都把半徑的最左邊卡在目前最左邊的基地台,被半徑覆蓋住的就忽略它,做到沒有基地台為止
bool is_legal(int r){
int cover = 0; // 最右側覆蓋位置
int stand = 0; // 用了幾個基地台
for(int i=0; i<n; i++){
if(arr[i] > cover){
cover = arr[i] + r;
stand++;
}
}
if(stand > k) return false; // 基地台數量不符合
else return true;
}
然後勒?
給 \(N\) 個電信公司需要服務的據點的座標 \(x_i\)
並且最多可以架設 \(K\) 個基地台在任一座標位置
每個基地台服務的半徑範圍皆一樣
求半徑至少為多少可以覆蓋所有據點?
\(1 \le K<N \le 50000, \ 0 \le x_i \le 10^9\)
如果目前的半徑可以覆蓋所有據點
那麼比這個半徑大的都可以覆蓋所有據點
半徑和能不能覆蓋成正比
所以我們就可以對半徑二分搜!
AC code
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define endl '\n'
#define AI(x) begin(x),end(x)
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int arr[50005];
int n, k;
bool is_legal(int r){
int cover = 0; // 最右側覆蓋位置
int stand = 0; // 用了幾個基地台
for(int i=0; i<n; i++){
if(arr[i] > cover){
cover = arr[i] + r;
stand++;
}
}
if(stand > k) return false; // 基地台數量不符合
else return true;
}
signed main(){_
cin >> n >> k;
for (int i = 0; i < n; ++i) {
cin >> arr[i];
}
sort(arr, arr+n);
int l = 0, r = 1e9+5;
while (l < r) { // 左閉右閉 維護1區間
int mid = l + (r - l) / 2;
if (is_legal(mid)) {
r = mid;
} else {
l = mid + 1;
}
}
cout << l << endl;
return 0;
}
練習題
問訓練幾天之後可以贏過對手
一樣觀察,什麼東西有單調性?
訓練越多天,越可能贏!
作法:
對訓練天數二分搜
check( x ) : 計算訓練x天可不可行
how? 直接算出每匹馬的強度,sort,賽跑!
more and more題目
STL的二分搜
upper_bound() / lower_bound()
#include <iostream>
#include <set>
using namespace std;
int main() {
//set
s.upper_bound(x);//O(log N)
upper_bound(s.begin(),s.end(),x);//O(n)
//vector or deque
//記得先sort
upper_bound(v.begin(),v.end(),x);//O(log n)
}
回傳sort 過的容器中 大於 / 大於等於 x 的第一個物品的iterator
注意:set的寫法要和vector不一樣
Divide and Conquer
分治
(DQ)
從一個問題開始
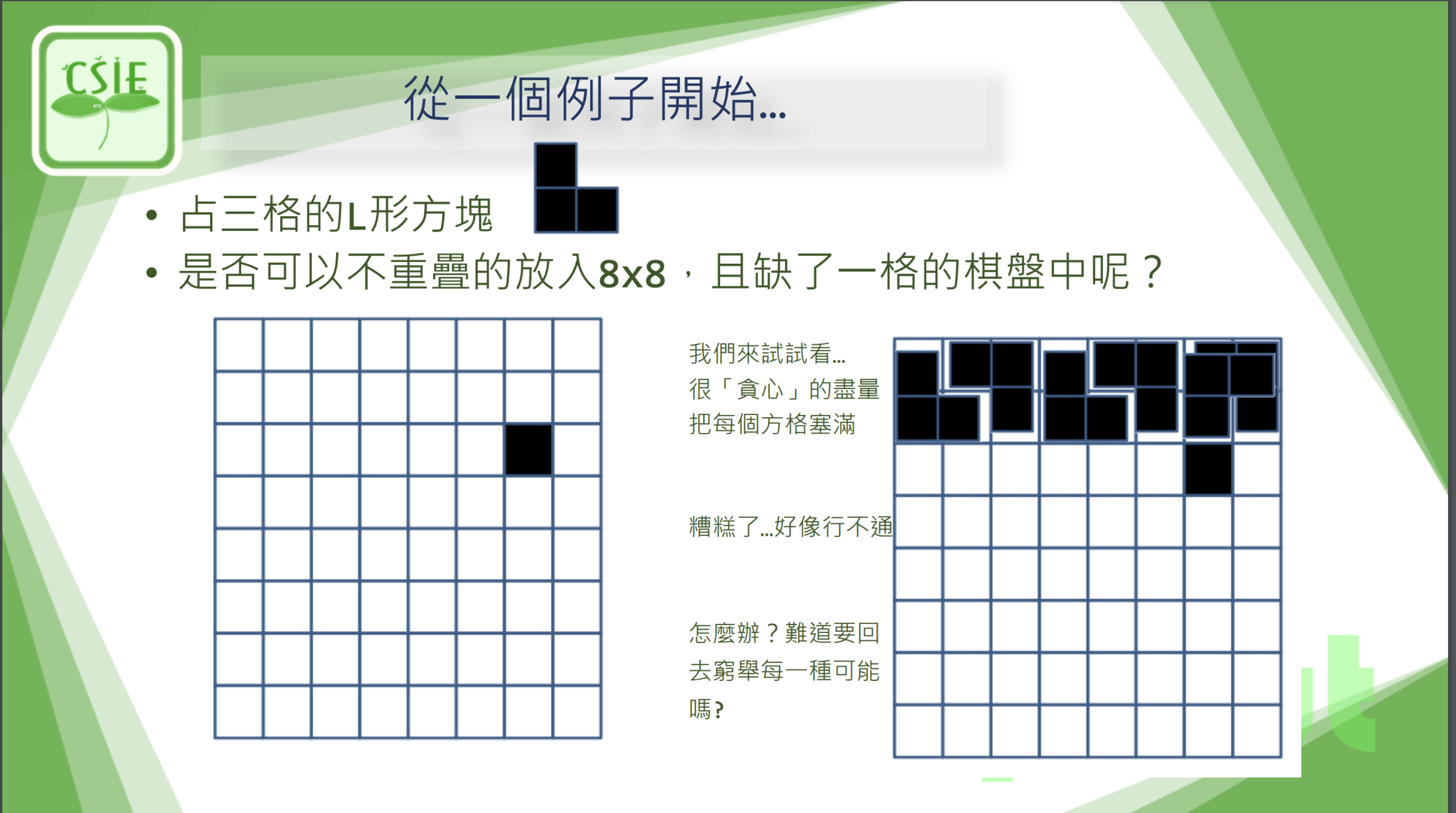
先不要想想8*8好了
從簡單的開始
如果2*2一樣缺一格
要怎麼做?

看起來簡單到不能再簡單
那4*4勒?
要怎麼做?
有沒有辦法說把它變成我們會做的2*2的樣子?
有!

先放一塊...
變成4個2*2了!
同理,8*8也可以先變成4*4,再變成2*2,再取得答案!
像這種每次把東西變一半
再把答案合起來的技巧
就叫做分治
注意:分治跟剛剛的二分搜沒有關係
分治的基本想法:
把大問題化為小問題,而小問題對我們根本不是問題
再合併小問題的答案
得到原本的大問題答案!
如何實作? 遞迴!!!
不過今天應該來不及講實作技巧和題目w
寫分治要做的事情:
- 怎麼分
-
解決子問題
-
怎麼合
再來看看一個分治的經典
merge sort
1. 分成子問題
把序列切一半
2. 解決子問題
遞迴處理(先假設做得到)
3. 合併子問題
假設有兩個已排序好的序列,要怎麼有效率地將它們合併成一個?
| 1 | 3 | 5 | 8 | 9 |
|---|---|---|---|---|
| 1 | 2 | 2 | 7 |
1
1
2
2
3
5
7
8
9
聽懂了ㄇ?
從兩個子陣列中,選較小的放入新的陣列!
O(n)
2 1 4 4,7 8 3 6 4,7
1,2 4,4,7 3,8 4,6,7
7 4 4 7
1,2,4,4,7 3,4,6,7,8
1,2,3,4,4,4,6,7,8
這樣有 O(logn)層
每層都是O(n)
所以就能O(nlogn)排序了!!
差不多講到這樣
進階思考:
逆序數對
想想看要怎麼做吧
下課摟

開始報名了快去啦