
Astro-Model
Методы математического моделирования в проектном обучении астрономии
Докладчик
Байгашов Алексей Сергеевич

Коллектив проекта

Работа с детьми

Курс: Школа Юного Астронома
(БФУ им. И. Канта)

Курс: Математическое моделирование
(БФУ им. И. Канта)
(лектор - д.ф.-м.н. Асташенок А. А.)

Популяризация науки

Астрономический лекторий
(лектор - д.ф.-м.н. Никитин М. А.)

Мероприятие "Дни открытой астрономии"
(коллеги из клуба - любителей "Kenig-Astro")

Астрономические выезды



Олимпиадные результаты

ВОШ по астрономии 2018 г.
Юшкин Матвей - призер

ВОШ по астрономии 2020 г.
Шаронова Александра - призер

Проектные результаты


Конкурс: "Народное достояние России"

Конференция им. Вернадского

Президентский грант


Основная идея





Научная работа
Наблюдения / эксперимент
Решение задачи / отчетная статья
Публикация результатов
Защита результатов
Личный кабинет на сайте Astro-Model


Научный блок
Общий вид

Принцип публикации статьи
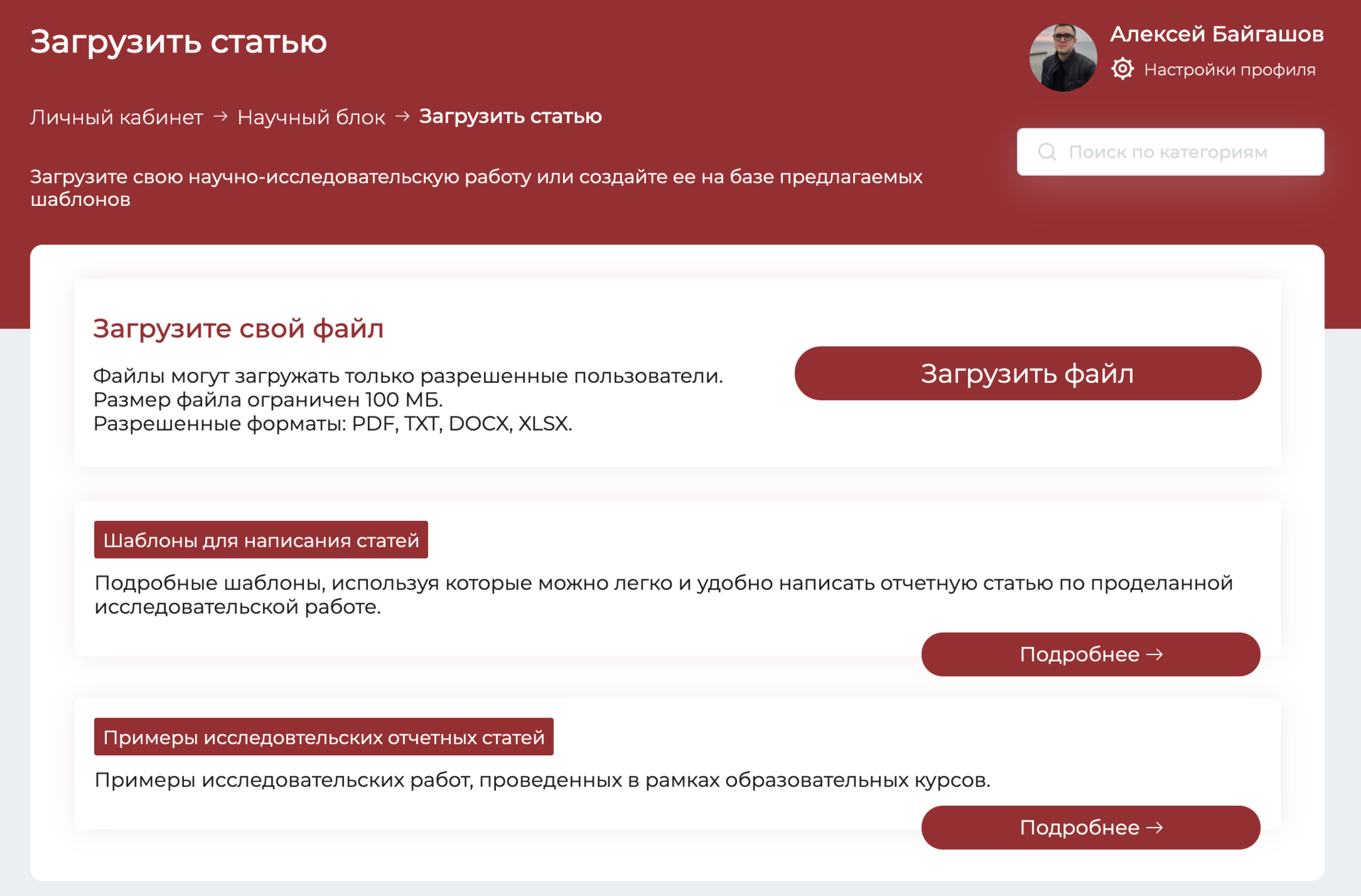
Шаблоны статей
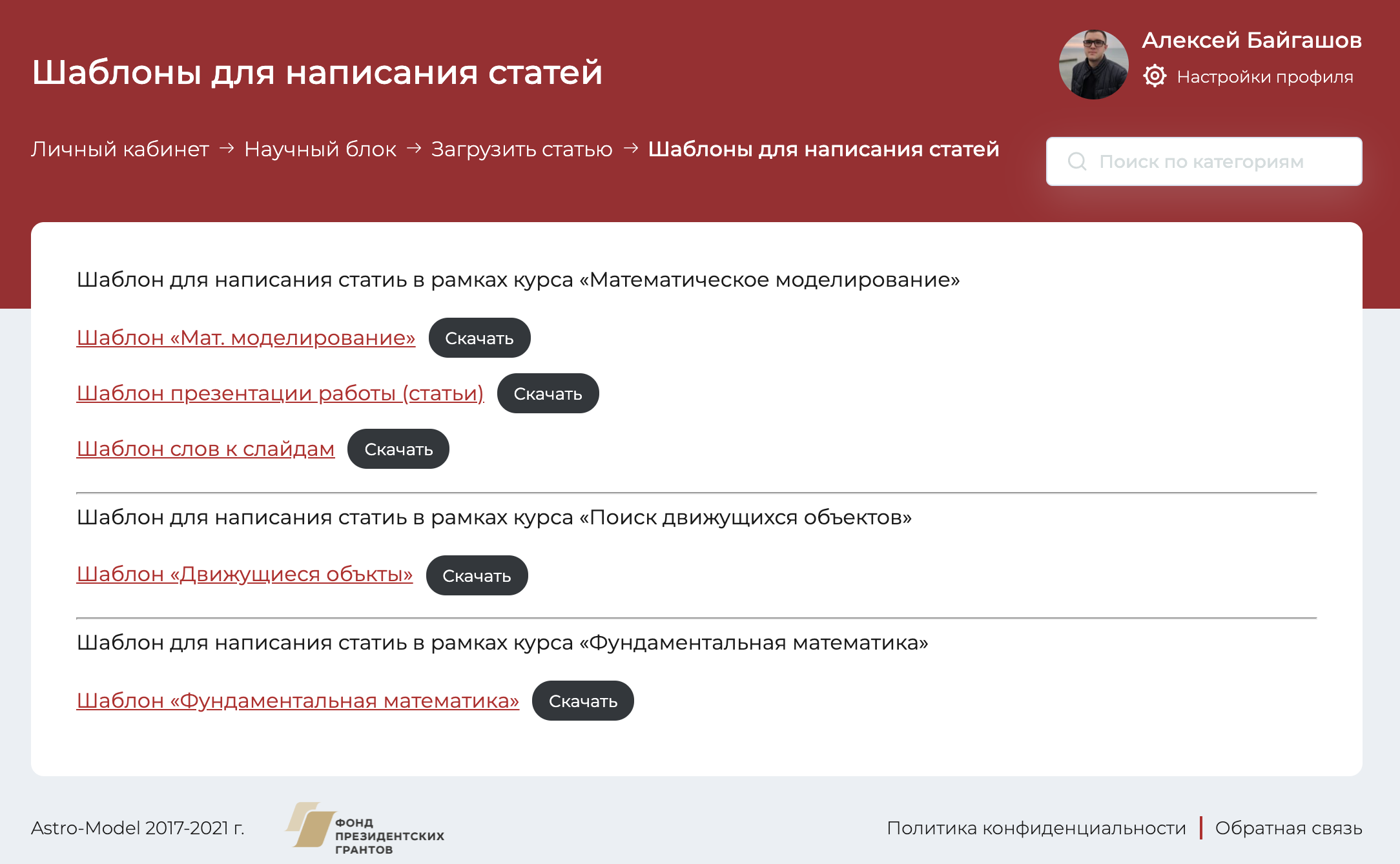

Архив статей

Архив статей
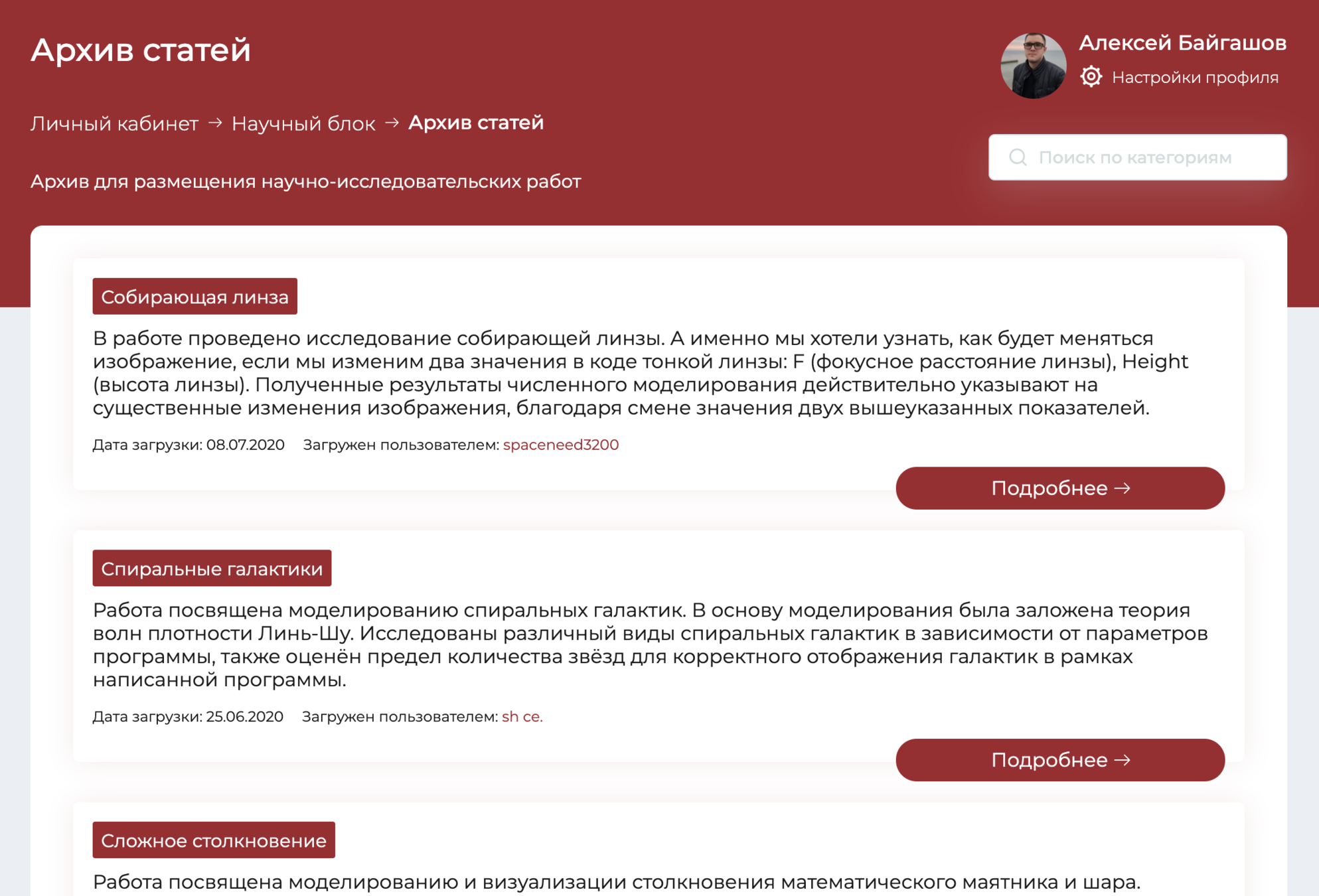
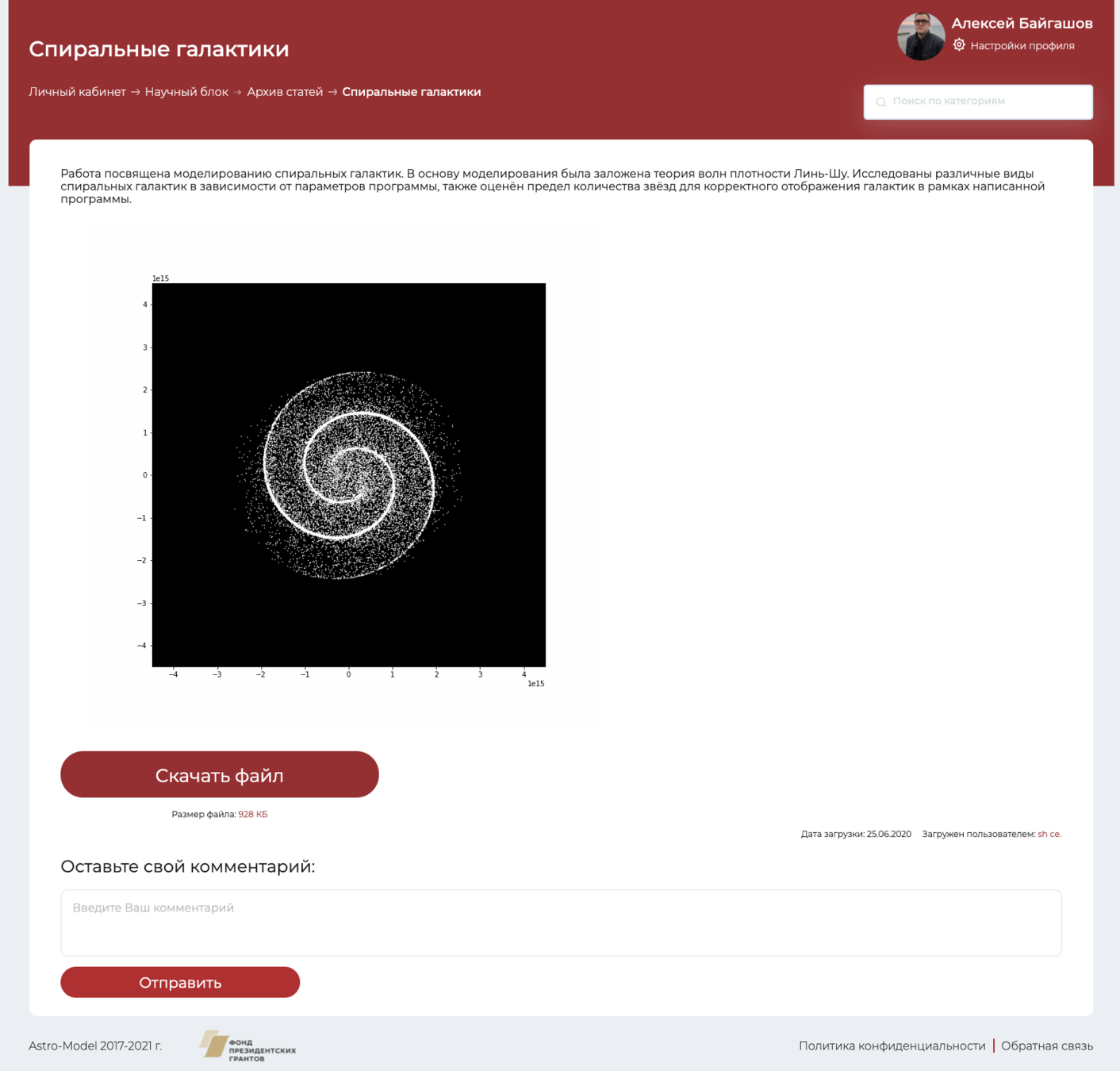
Примеры работ школьников


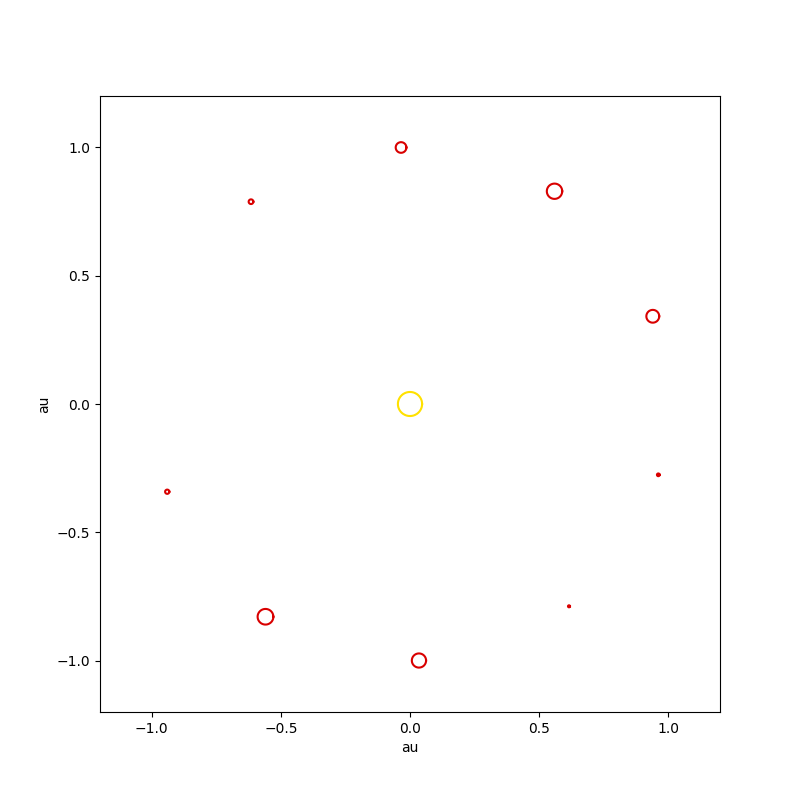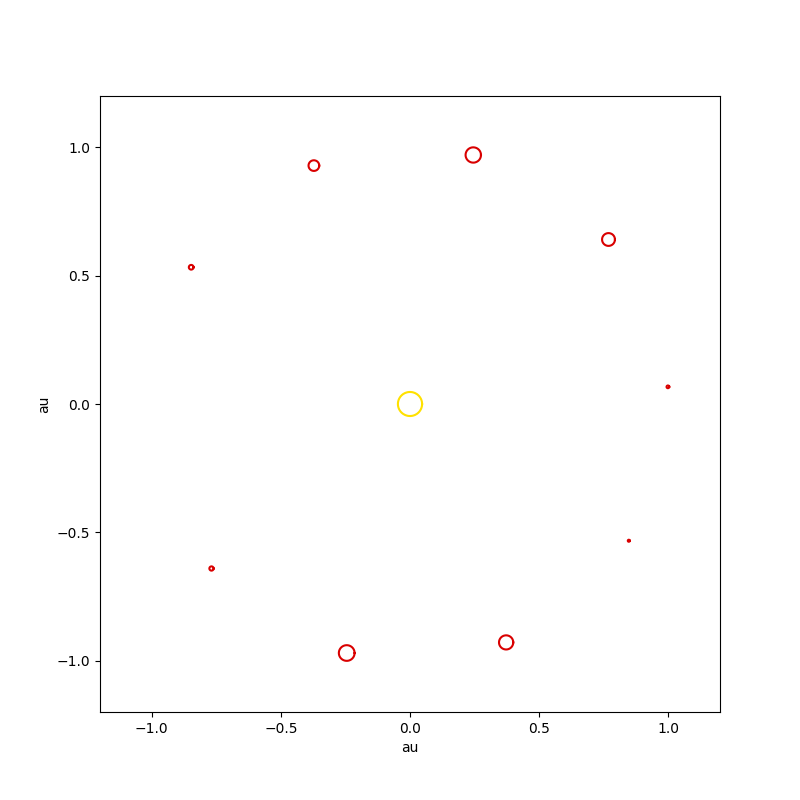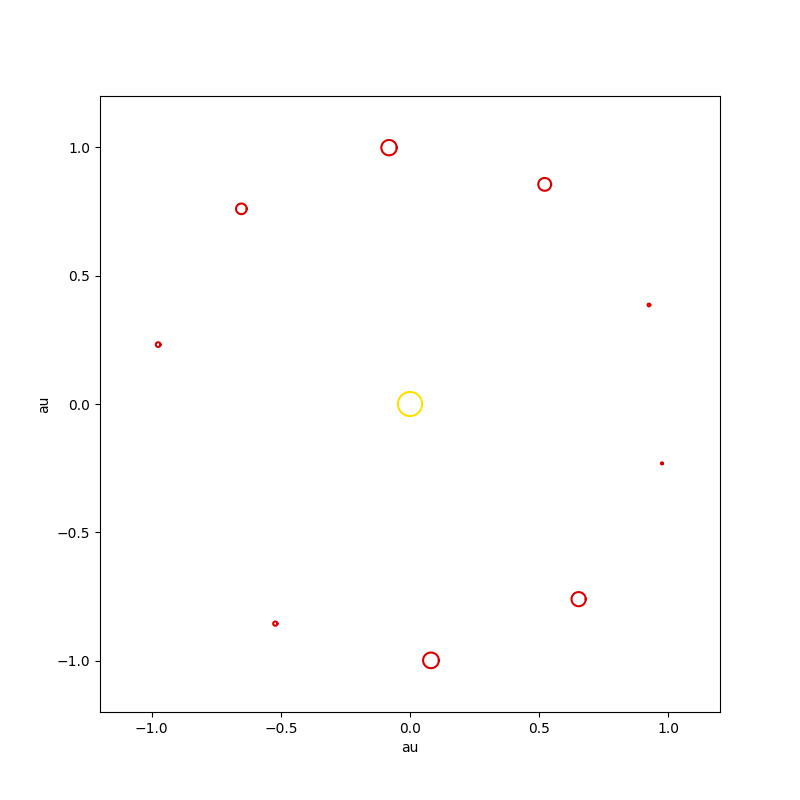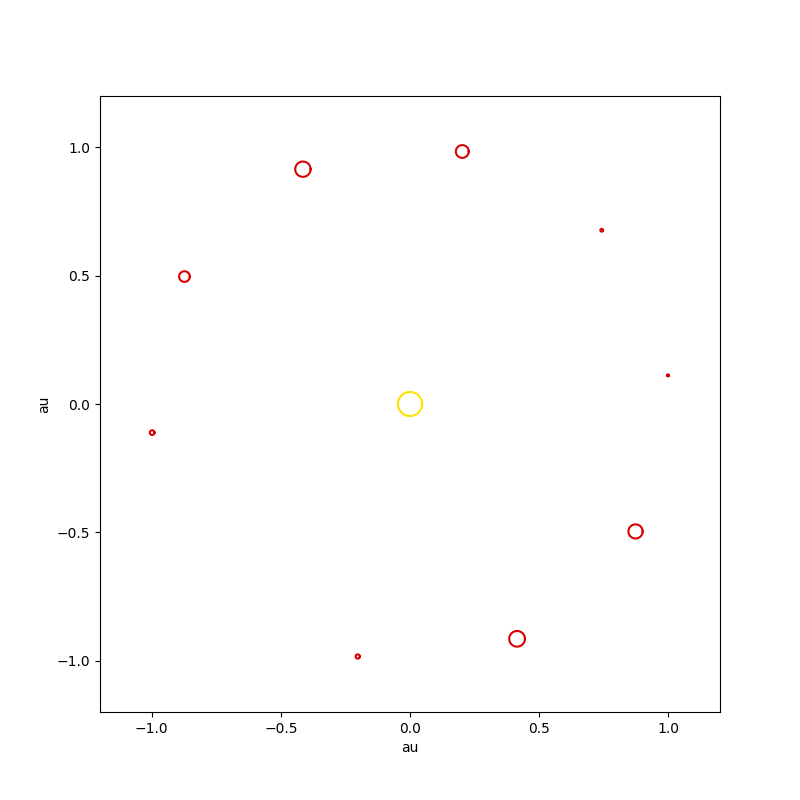
Спиральные галактики
Моделирование системы колец массивных тел
Примеры работ школьников


Взрыв сверхновой
К явлению радуги
Примеры работ школьников


Броуновское движение
Бильярдные шары
Примеры работ школьников


Забавная горка
Сложное столкновение

Образовательный блок
Проектные блоки

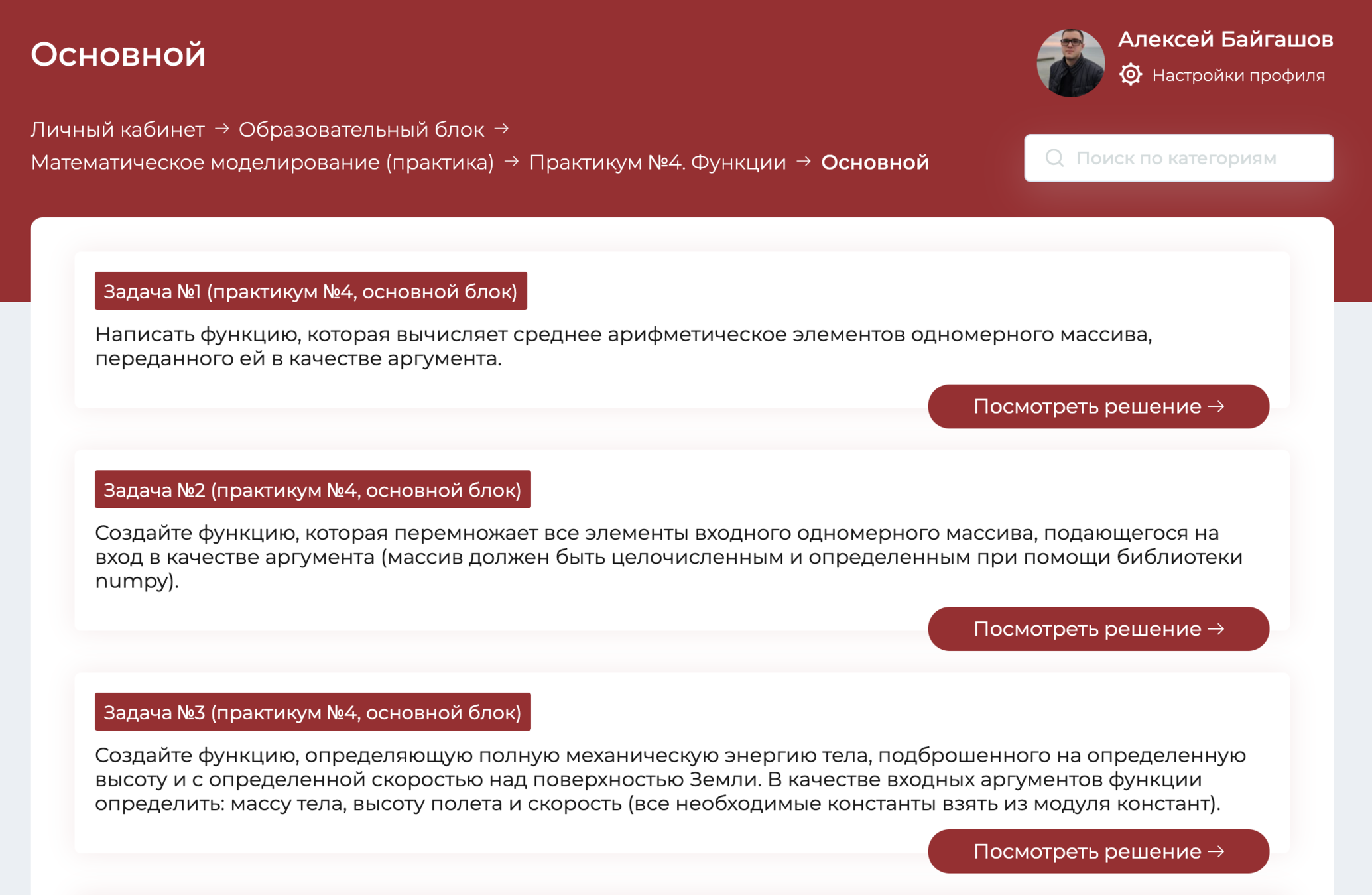
Математическое моделирование


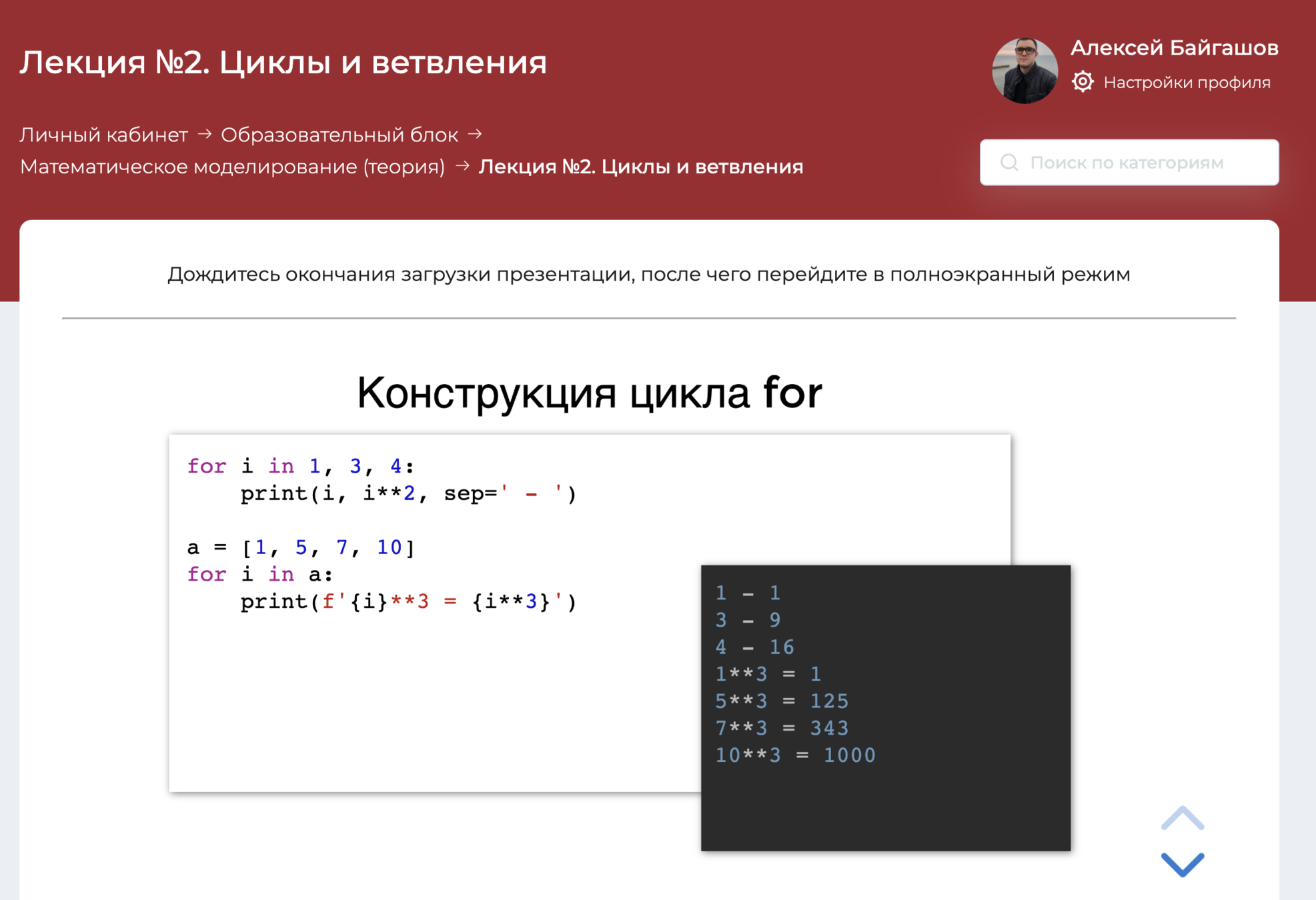
Python 3



Виды уравнений
линейное уравнение
квадратное уравнение
кубическое уравнение
трансцендентное уравнение
дифференциальное уравнение

Дифференциальное уравнение
Дифференциальное уравнение – уравнение, в которое входят производные функции, и может входить сама функция, независимая переменная и параметры.
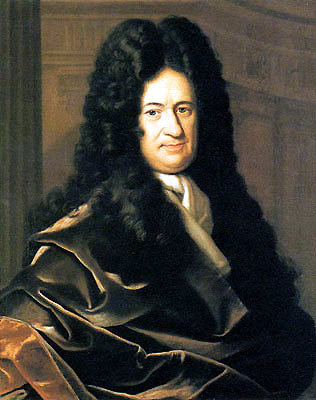




Алгоритм постановки
Алгоритма нет!
Методика:
• определитель изменяемую функцию "f(x)"
• определить независимую переменную величину "x"
• определить начальные условия

Пример - задача
Из эксперимента известно, что скорость радиоактивного распада пропорциональна количеству вещества. Определить закон изменения количества вещества со временем и найти период, за который распадется половина вещества (период полураспада).


Постановка диф. задачи
Дано:
Найти:
Начальное условие:
изменяемая величина -
количество вещества
переменная величина -
время
закон изменения
со временем:
Решение:
это исходя из условий задачи
минус – означает, что величина уменьшается

Постановка диф. задачи
изменение, малое, но конечное



Постановка диф. задачи

бесконечно малое изменение

В итоге
средняя скорость изменения
Дифференциальное уравнение
мгновенная скорость изменения

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# Пределы изменения переменной величины
# В данной задаче переменной величиной является время
t = np.arange(0, 10**6, 100)
# Запись диф. уравнения в виде функции
def radio_function(m, t):
dmdt = - k * m
return dmdt
# Определение начальных условий и параметров
m_0 = 10
k = 1.61*10**(-6) # Постоянная распада для Висмута 210
Алгоритм численного решения
'''
k_Ur_238 = 4.84*10**(-18) # Уран 238
k_Tl_210 = 8.76*10**(-3) # Талий 210
'''
# Решение дифференциального уравнения функцией odeint
solve_Bi = odeint(radio_function, m_0, t)
# Построение решения в виде графика функции
plt.plot(t, solve_Bi[:,0], label='Распад Висмута 210')
plt.xlabel('Период распада, секунды')
plt.ylabel('Функция распада')
plt.title('Радиоактивный распад')
plt.legend()
plt.show()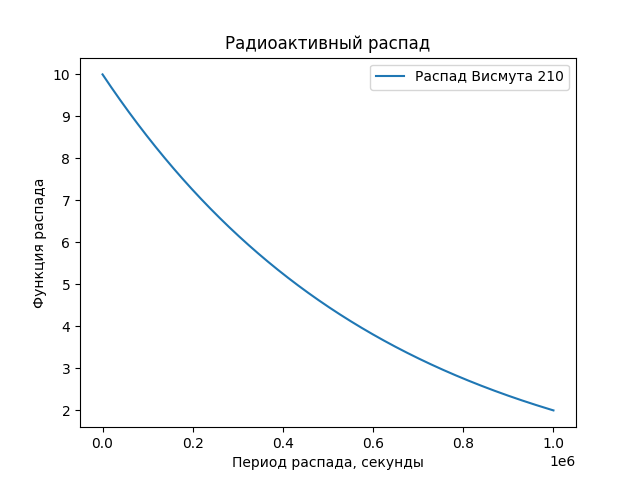

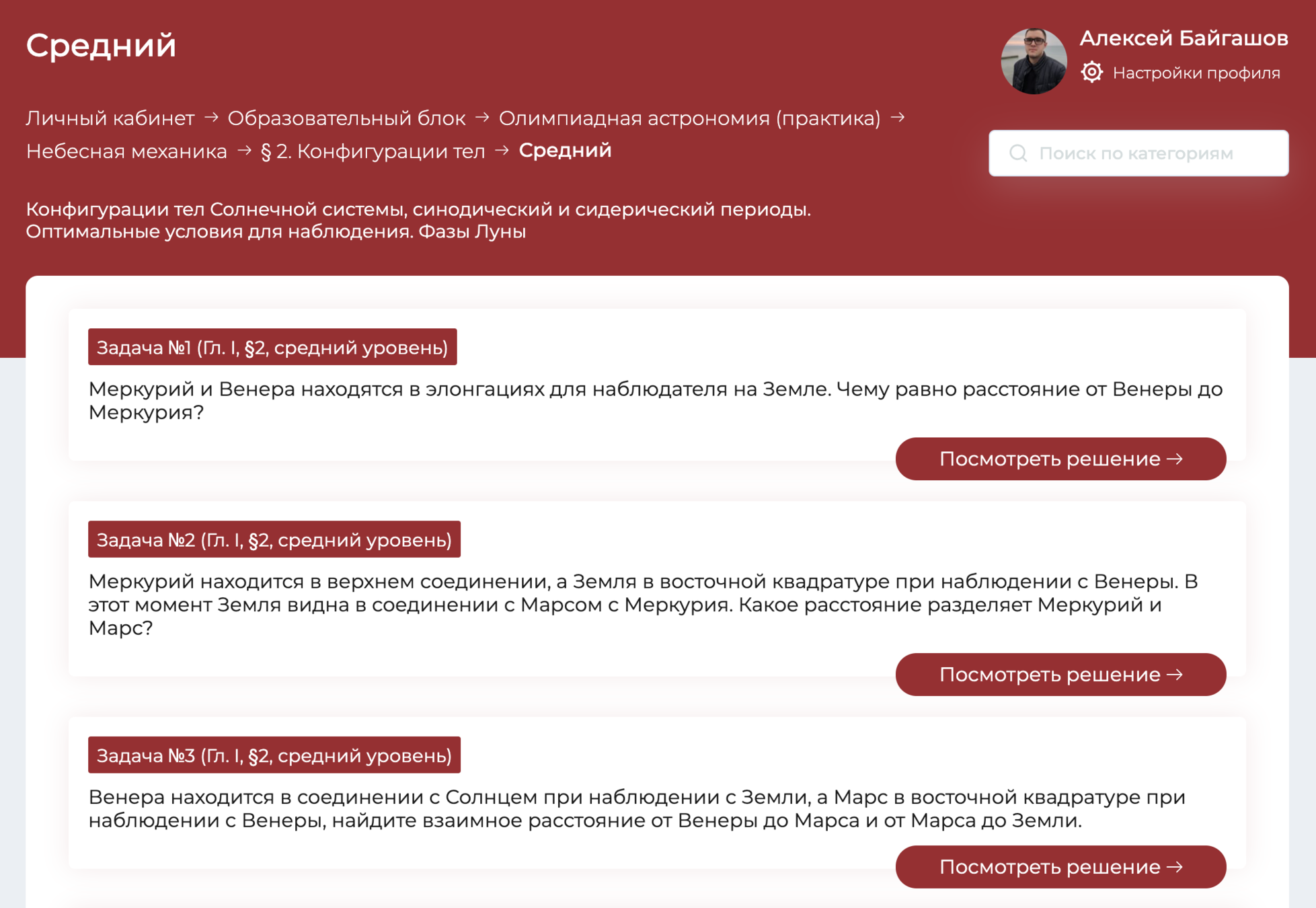
Школьные задачи, сводимые к диф. уравнениям
Математическое моделирование

Математическое моделирование

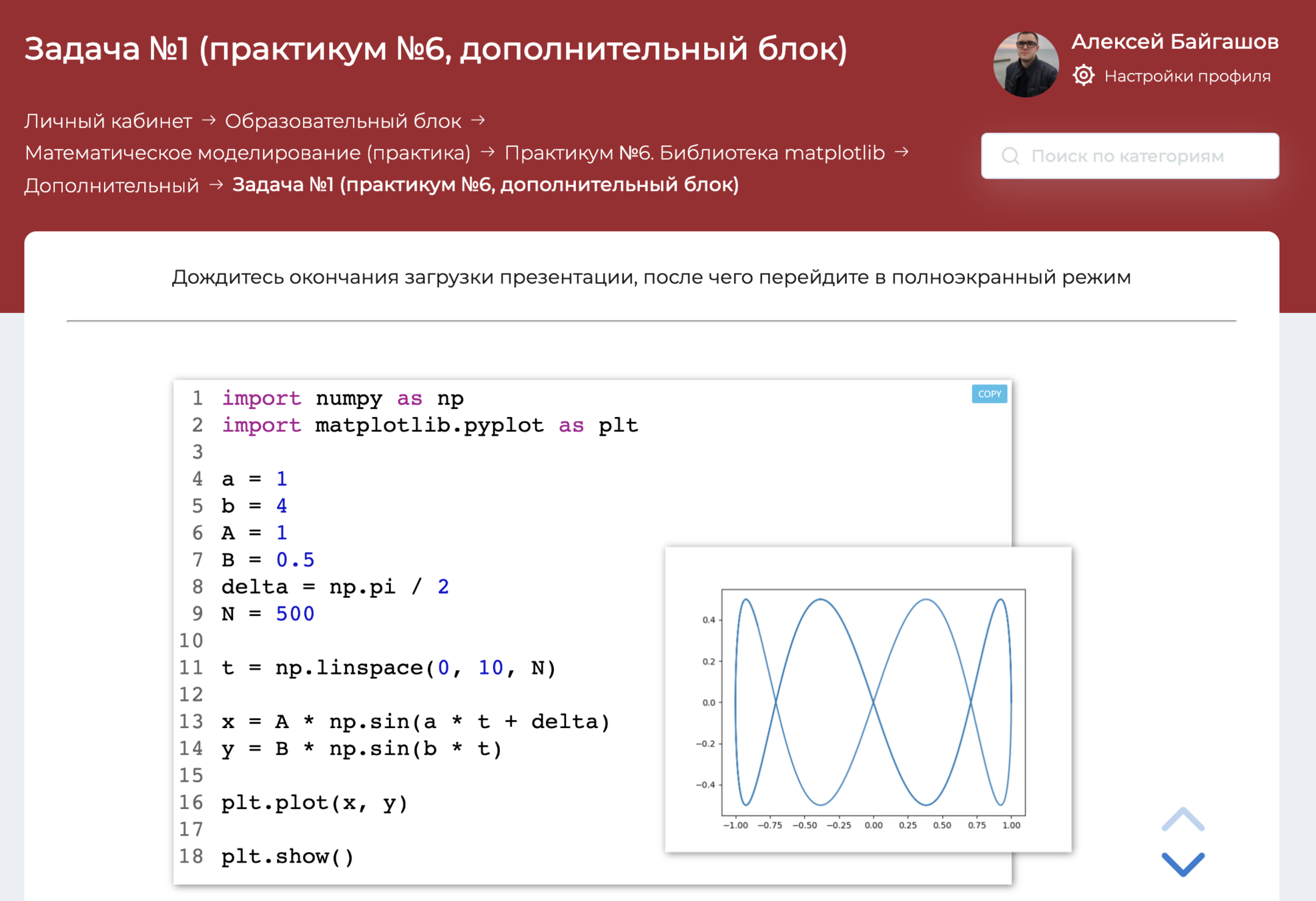

Блок моделирования

Общий вид


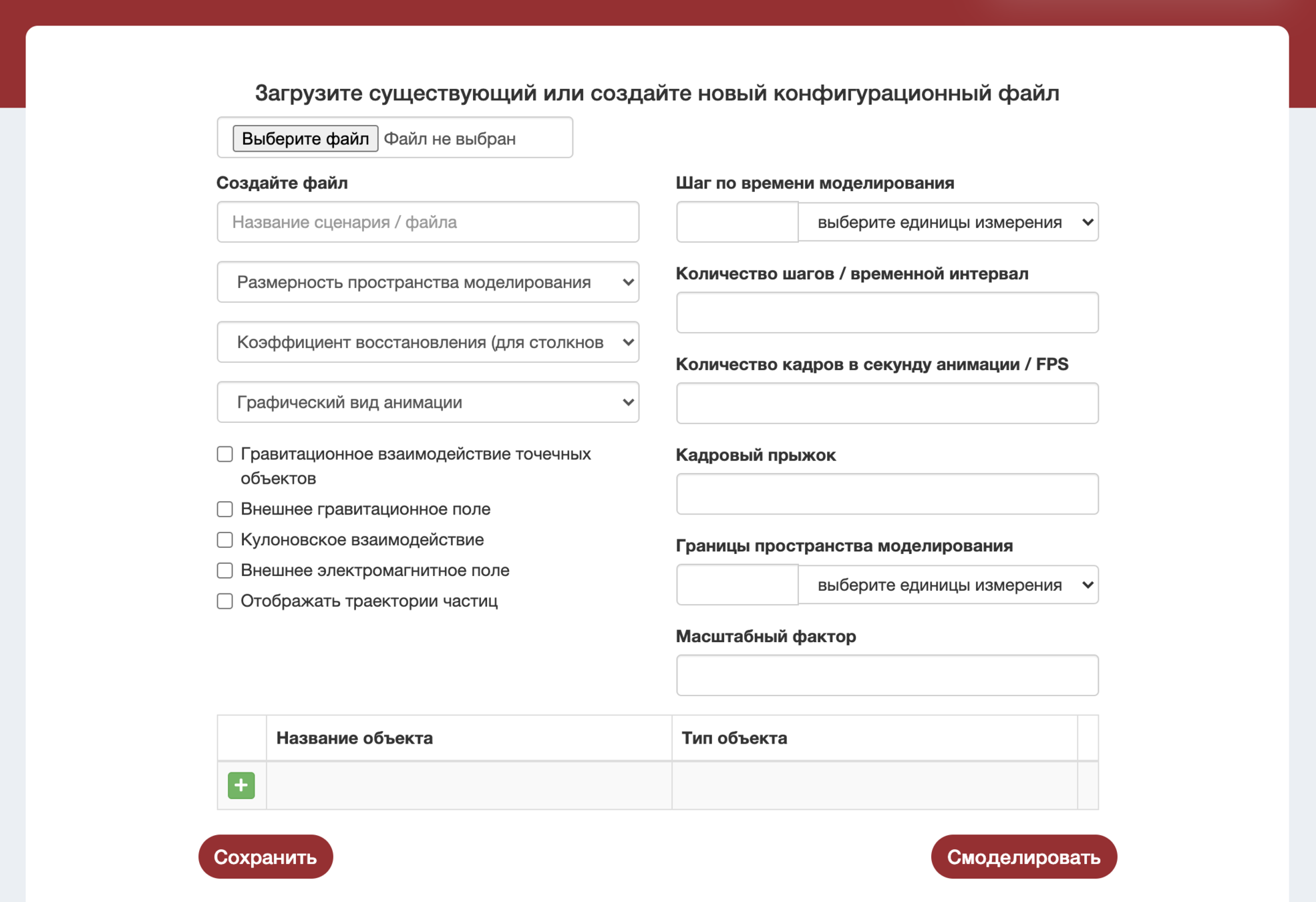
Конфигуратор моделирования

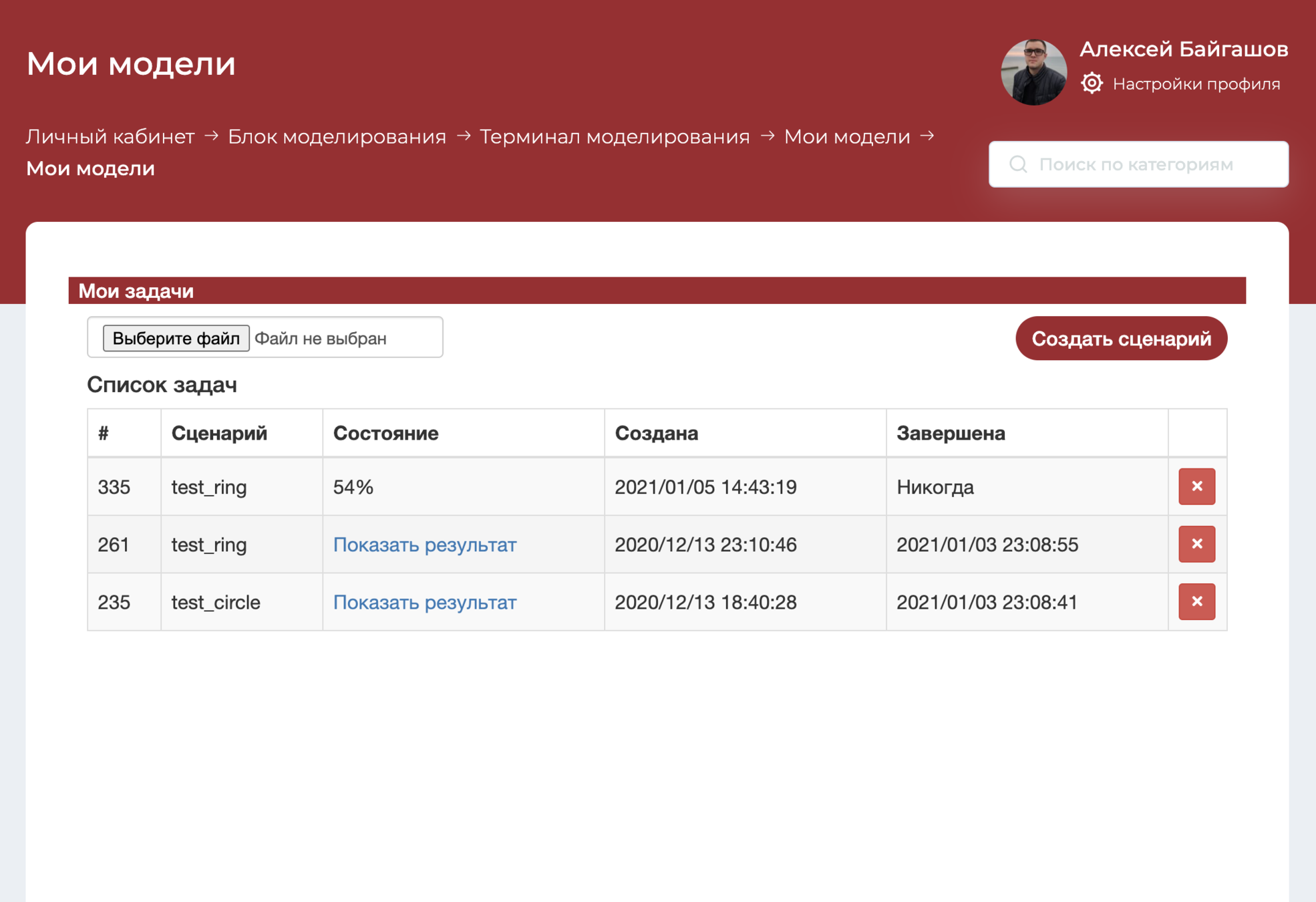
Терминал моделирования

Астрономическое образование

Олимпиадная астрономия


Познавательный блок


Заключение
1. Математическое моделирование - эффективный инструмент проектного обучения астрономии
2. Платформа Astro-Model - универсальная среда очного и дистанционного обучения
3. Использование авторских методик и инструментов обеспечивает высокие результаты наших учеников
Контактные данные:
a.baigashov@gmail.com
astrobfu@gmail.com
