An introduction to gradient descent algorithms

 Abdellah CHKIFA

abdellah.chkifa@um6p.ma

Outline

1. Gradient Descent

  • Gradient Descent
  • Linear regression
  • Batch Gradient Descent
  • Stochastic Gradient Descent 

2. ​Back-propagation

  • Logistic regression
  • Soft-max regression
  • Neural networks
  • Deep neural networks

Gradient Descent: an intuitive algorithm

objective function (also called loss function or cost function etc.)

\theta^{(k+1)} = \theta^{(k)} - \eta \nabla f (\theta^{(k)})
f
\theta^{(0)}

initial guess

min_{\theta \in \Omega} f(\theta)

Importance of learning rate

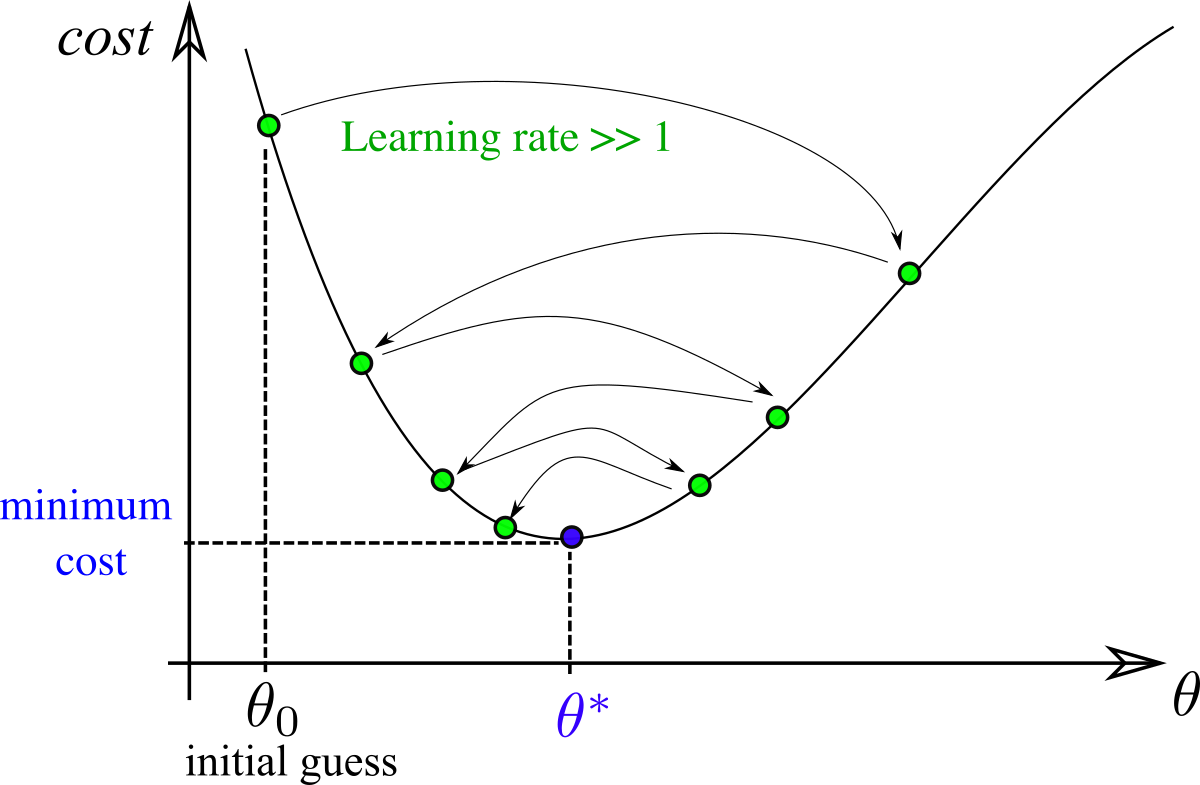
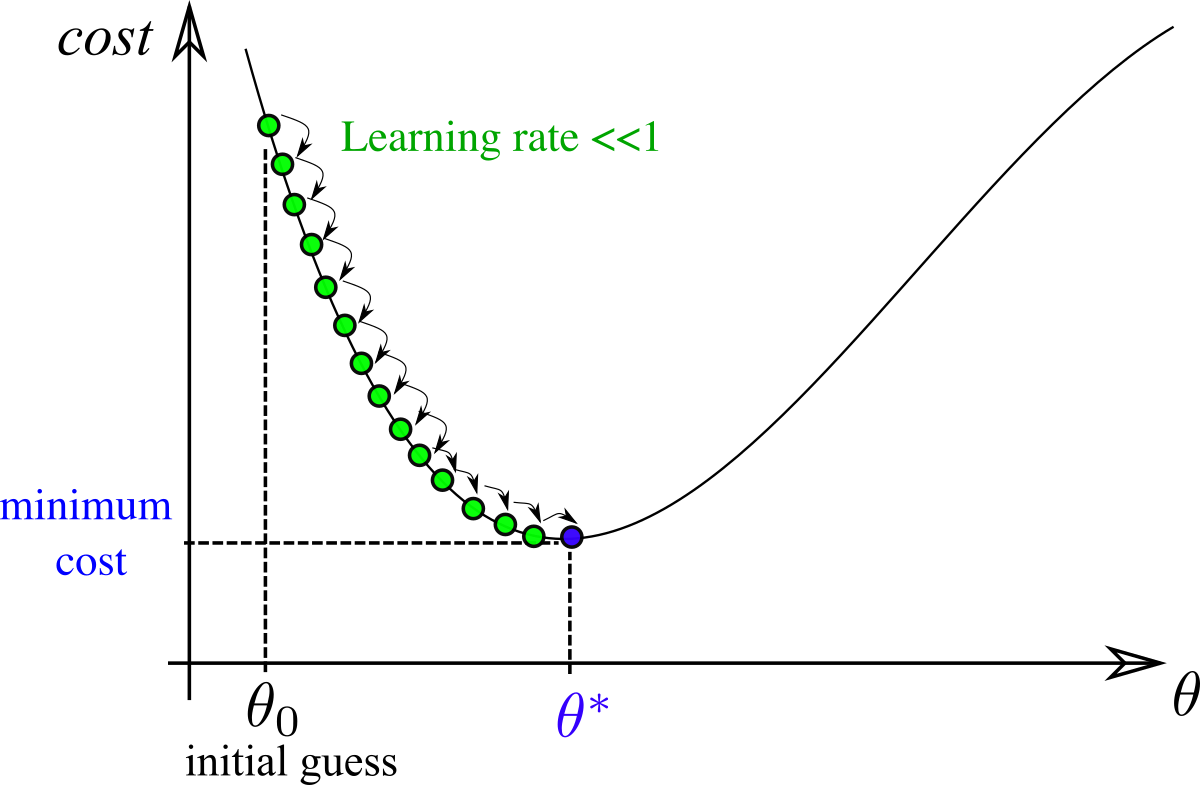
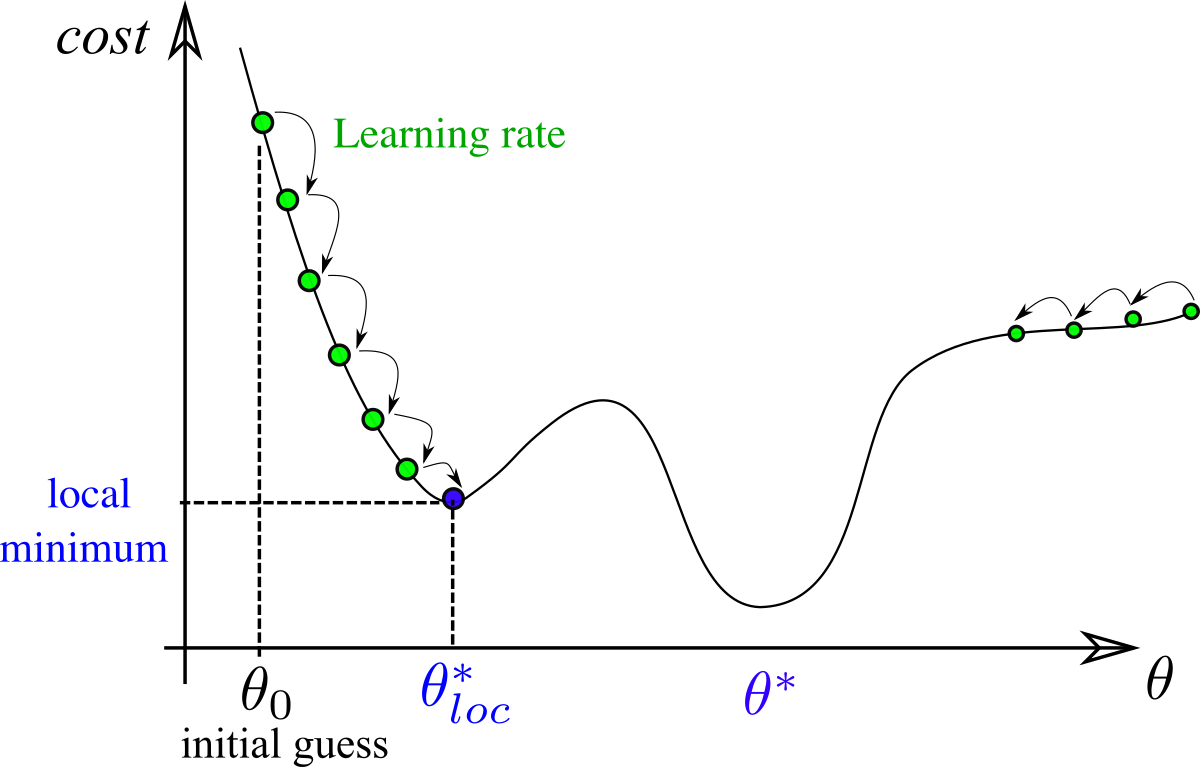
We consider GD applied to

f: x\mapsto x^2

with

x_0=4

and rates

\eta=0.1
\eta=0.01
\eta=0.9
\eta=1.01

Gradient Descent: a convergence theorem

\theta^{(k+1)} = \theta^{(k)} - \eta \nabla f (\theta^{(k)})
\theta^{(0)}

initial guess

f(t\theta + (1-t)\theta') \leq t f(\theta) + (1-t) \theta',\quad\quad \theta,\theta'\in{\mathbb R^d}, t\in [0,1]

  f    convex:

  f    L-smooth:

\| \nabla f(\theta) - \nabla f(\theta')\| \leq L \|\theta-\theta'\|,\quad\quad \theta,\theta'\in{\mathbb R^d}.

Suppose that f is convex and L-smooth. The gradient descent algorithm with η < 1/L converge to θ* and yields the convergence rate

 

 

2
f: \R^d \to R
0 \leq f(\theta^{(k)}) - f(\theta^*) \leq \frac {\|\theta^{(0)} - \theta^*\|^2}{2\eta k}

Theorem

Gradient Descent: a convergence theorems

\theta^{(k+1)} = \theta^{(k)} - \eta \nabla f (\theta^{(k)})
\theta^{(0)}

initial guess

f     μ-strongly convex:

f: \R^d \to R
f(\theta') \geq f(\theta) + ⟨ \nabla f(\theta), \theta'-\theta ⟩ + \frac \mu 2 \|\theta'-\theta\|^2 ,\quad \quad \theta,\theta'\in{\mathbb R^d}.

suppose that f is μ-strongly convex and L-smooth. The gradient descent algorithm with η < 1/L converge to θ* with

\| \theta^{(k)} - \theta^* \| \leq (1-\eta \mu)^k \|\theta^{(0)} - \theta^* \|

Theorem

μ-strong convexity can be weakened to Polyak-Lojasiewicz Condition 🔗

  • Easy to implement.

  • Each iteration is (relatively!) cheap, computation of one gradient.

  • Can be very fast for smooth objective functions, as shown.
  • The coefficient L may not be accurately estimated.

  • => Choice of small  learning rate.

  • Concrete objective functions  are usually not strongly convex nor convex.

  • GD does not handle non-differentiable functions (biggest downside).

Pros and Cons

Reference

https://www.stat.cmu.edu/~ryantibs/convexopt/

Part 2

Made with Slides.com