Google just built a quantum computer(?), and Pakistan is sitting ducks!
Abdullah Khalid
Quantum Information Scientist
Guftugu Seminar Series
11th November 2019

How to prepare for the coming quantum computing age.
What is a computer?



Chemistry
Biology
Computer science
Computing Machine = Physical System
Computers solve computational problems



Decision
Search
Optimization
Decision Problems
Multiplication
Input: integers P and Q
Output: integer R = P x Q

Factorization
Input: integer R
Ouput: prime numbers P and Q
such that R = P x Q
R = 21
digits = 2
R = 498556150811
digits = 12 = problem size
General number field sieve algorithm

Computational Complexity
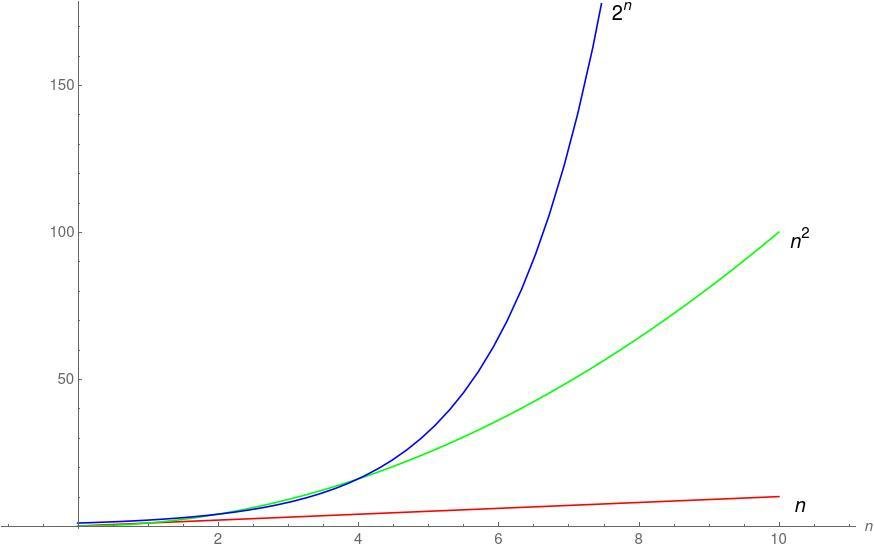
Multiplication
Factorization
Resources = time/memory
Problem size (n)
Hard/inefficient
Easy/efficient
Application of computation: Cryptography

"Top secret info"
"Top secret info"
"hf72h18v82ja9"
You
You
Military
Bank
Email provider
Military

RSA encryption protocol

Encryption/Decryption = Multiplication = Easy
Cracking = Factorization = Hard
Rivest–Shamir–Adleman
Key: 10101011101...
Security ∝ number of digits

Recommended key size: 4096 bits
(for security till 2030)
Cracking RSA
Sampling Problems
Binomial sampling
Input: n, p
Output: a sample from the binomial probability distribution
A random number generator!

"The underlying physical laws ... of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble." 1929

Simulation Problem
Simulating atoms, molecules and materials
Paul Dirac
Quantum Computers

Computing Machines = Physical Systems
=> Computational complexity is determined by physical laws



Visions of Quantum Computing
Simulating atoms, molecules and materials
Simulate this
By controlled experiments on this



Quantum Computers: The transport analogy
Laptop
Super computer
Quantitative
Qualitative
Quantum computer
Solve computational problem = Go from A to B
Quantum computers can
simulate atoms, molecules and materials,
exponentially faster than classical computers.

Quantum computers can
maybe do machine learning and optimization
exponentially faster than classical computers.

Quantum computers can
break all currently used asymmetric encryption protocols
exponentially faster than classical computers.


arXiv:1909.07353
Cryptographic Algorithms in Use
Quantum computers CANNOT
do industrial optimization
predict the stock market
optimize airline schedules
predict the stock market
optimize airline schedules
NP-Complete problems
exponentially faster than classical computers.

If this was true, quantum computers could solve NP-complete problems efficiently
But they don't!
Quantum vs Classical Computers

Breaking encryption on Quantum Computer
Text
NP-Complete Problems on Classical/Quantum Computer
Breaking encryption on Classical Computer
Resources
Problem size (n)
Quantum Computing Today


Road to Quantum Computers
Quantum computers
Quantum supremacy devices
Solve a (useless) problem exponentially faster than a classical computer
Solve a (useful) problem exponentially faster than a classical computer


Analogy


Nature | Vol 574 | 24 OCTOBER 2019

Quantum Random Circuit

Computational problem
Input: Circuit C
Output: a sample from the output probability distribution of C
Difficult for classical computer
Outputs = 2n Output strings, each with different probability

Google's superconducting chip
53+1 qubits, depth = 20
How to verify a device which you claim can't even be classically simulated?
Is quantum supreme?
Google's claim: 10,000 years on a state of the art supercomputer, using the best classical algorithm they could think of.
IBM's claim: Sorry, 2.5 days only, using our better classical algorithm!
Quantum device performance: 600 seconds to sample 3 million times
How do we prepare for the coming quantum computing world?
First Option: Post-Quantum Crypto Algorithms

arXiv:1909.07353
No proofs of security, but hope!
Second Option: Quantum Key Distribution

Secret key: 1011101111010... for symmetric key encryption
Second Option: Quantum Key Distribution

$5000-50,000