Pakistan, quantum computing and cryptography
Abdullah Khalid
Quantum Information Scientist
The Second Floor
3rd October 2019






(Human) Computer
1788
1700s
1950s

Mechanical Computer
1940s


Electronic Computers
Total world computing capacity
2 x 1020 – 1.5 x 1021 FLOPS
Computational Problems
Multiplication
Input: integers P and Q
Output: integer R = P x Q


Algorithms
Computational Problems
Factorization
Input: integer R
Ouput: prime numbers P and Q
such that R = P x Q
Algorithms
R = 21
digits = 2
R = 498556150811
digits = 12
- Dixon's algorithm
- Continued fraction factorization
- Quadratic sieve
- Rational sieve
- General number field sieve
- Shanks's square forms factorization

Computational Problems
Multiplication
Factorization
Cryptography

"Top secret info"
"Top secret info"
"hf72h18v82ja9"
You
You
Military
Bank
Email provider
Military

RSA encryption protocol

Encryption/Decryption = Multiplication
Cracking = Factorization
Rivest–Shamir–Adleman
Key: 10101011101...
Security ∝ number of digits

Recommended key size: 4096 bits
(for security till 2030)
Cracking RSA
Quantum Computers

Classical Physics
1600 onwards
Quantum Physics
1900 onwards


Newton Faraday




Einstein
Heisenberg
Born
Schrodinger

"The underlying physical laws ... of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble." 1929

Computational Problem
Simulating atoms, molecules and materials
Paul Dirac
Birth of Quantum Computers
Simulating atoms, molecules and materials
"Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy." Richard Feynman, 1982



Quantum Computers: The transport analogy
Human computer
Super computer
Quantitative
Qualitative
Quantum computer
Computational problem: Go from A to B


Visions of Quantum Computing
Simulating atoms, molecules and materials
Simulate this
By controlled experiments on this
Quantum Computing Today




Quantum computers CANNOT
do industrial optimization
predict the stock market
optimize airline schedules
predict the stock market
optimize airline schedules
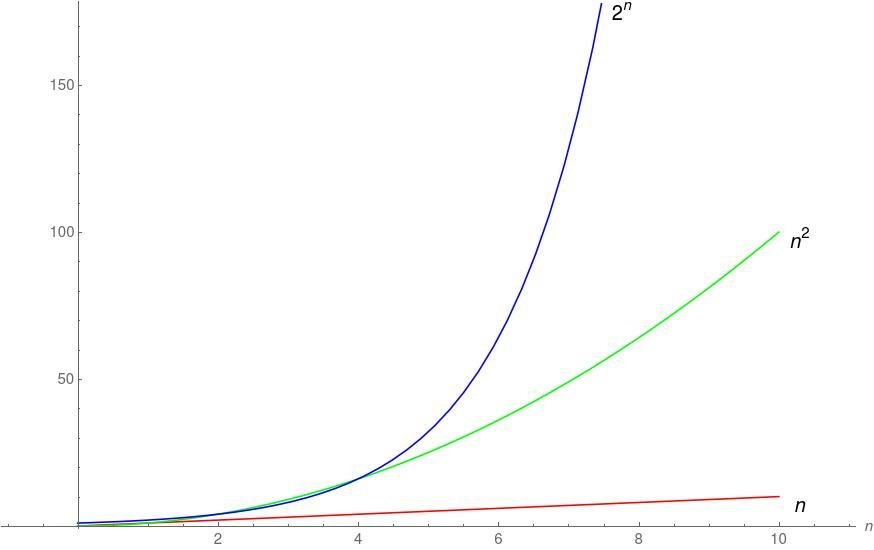
NP-Complete problems
exponentially faster than classical computers.
Quantum computers can
simulate atoms, molecules and materials,
exponentially faster than classical computers.

Quantum computers can
maybe do machine learning and optimization
exponentially faster than classical computers.

Quantum computers can
break all currently used asymmetric encryption protocols
exponentially faster than classical computers.

Quantum Computer

Breaking encryption on Quantum Computer
Text
NP-Complete Problems on Classical Computer
NP-Complete Problems on Quantum Computer
Breaking encryption on Classical Computer

arXiv:1909.07353
Cryptographic Algorithms in Use
How do we prepare for the a world where Quantum Computers exist?
First Option: Post-Quantum Crypto Algorithms

arXiv:1909.07353
No proofs of security, but hope!
Second Option: Quantum Key Distribution

Secret key: 1011101111010...
Second Option: Quantum Key Distribution

Provably secure against quantum computers
Second Option: Quantum Key Distribution

$5000-50,000
What should Pakistan do to prepare for the quantum computing future?
- Invest in quantum computing and cryptography research.
- Build quantum cryptography infrastructure.
- Invest in policy research.
- Participate in international encryption standards committees.