Recommendations in eCommerce. Basics

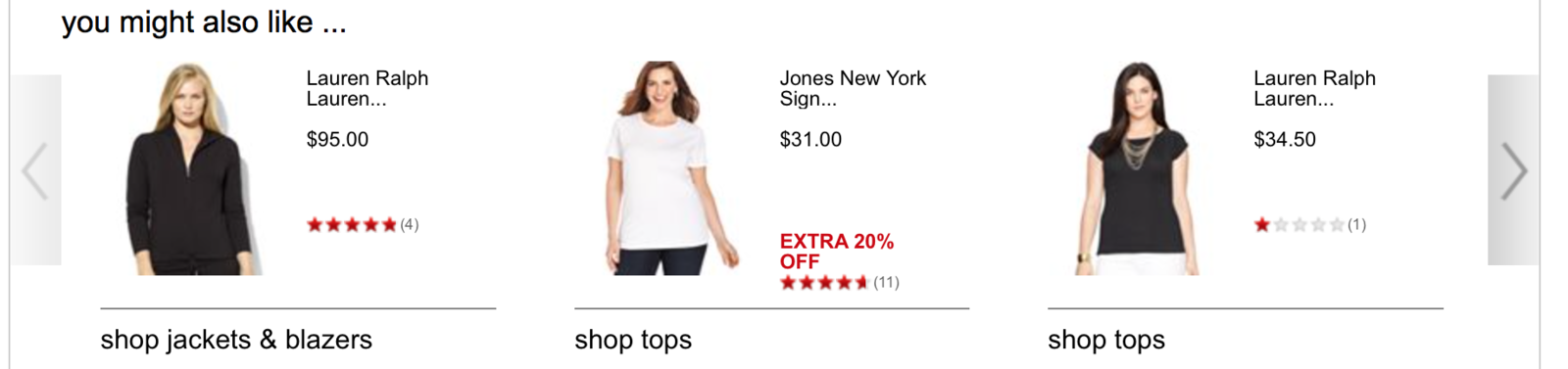
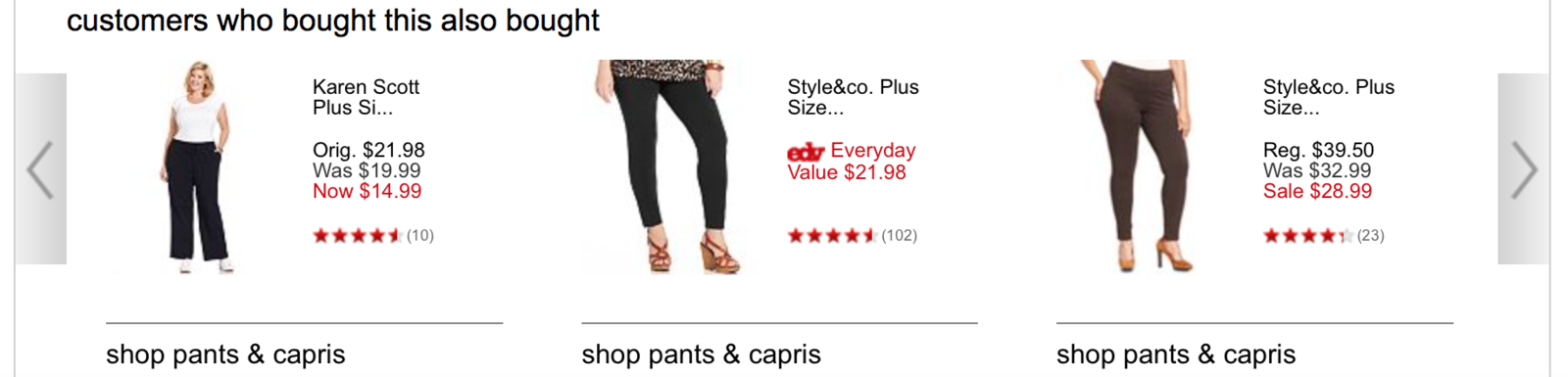
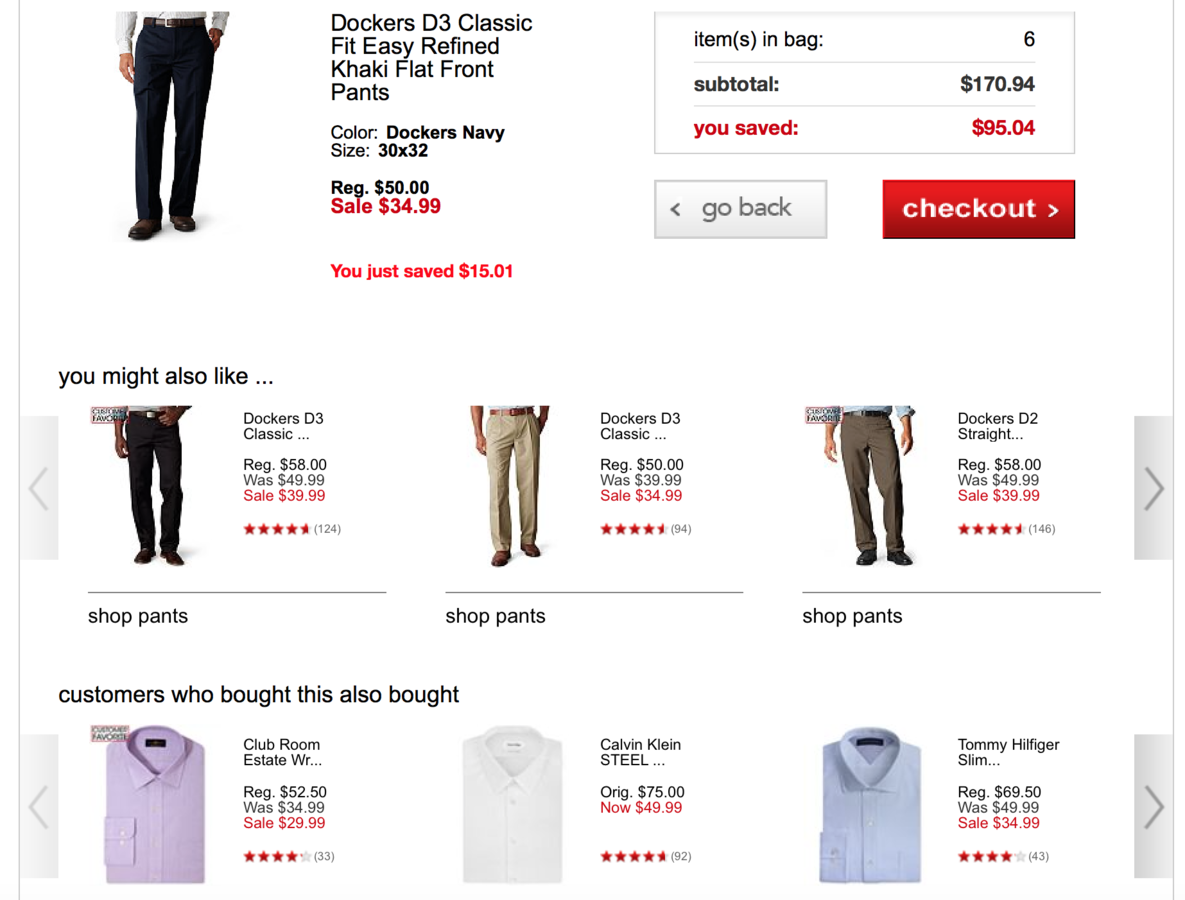
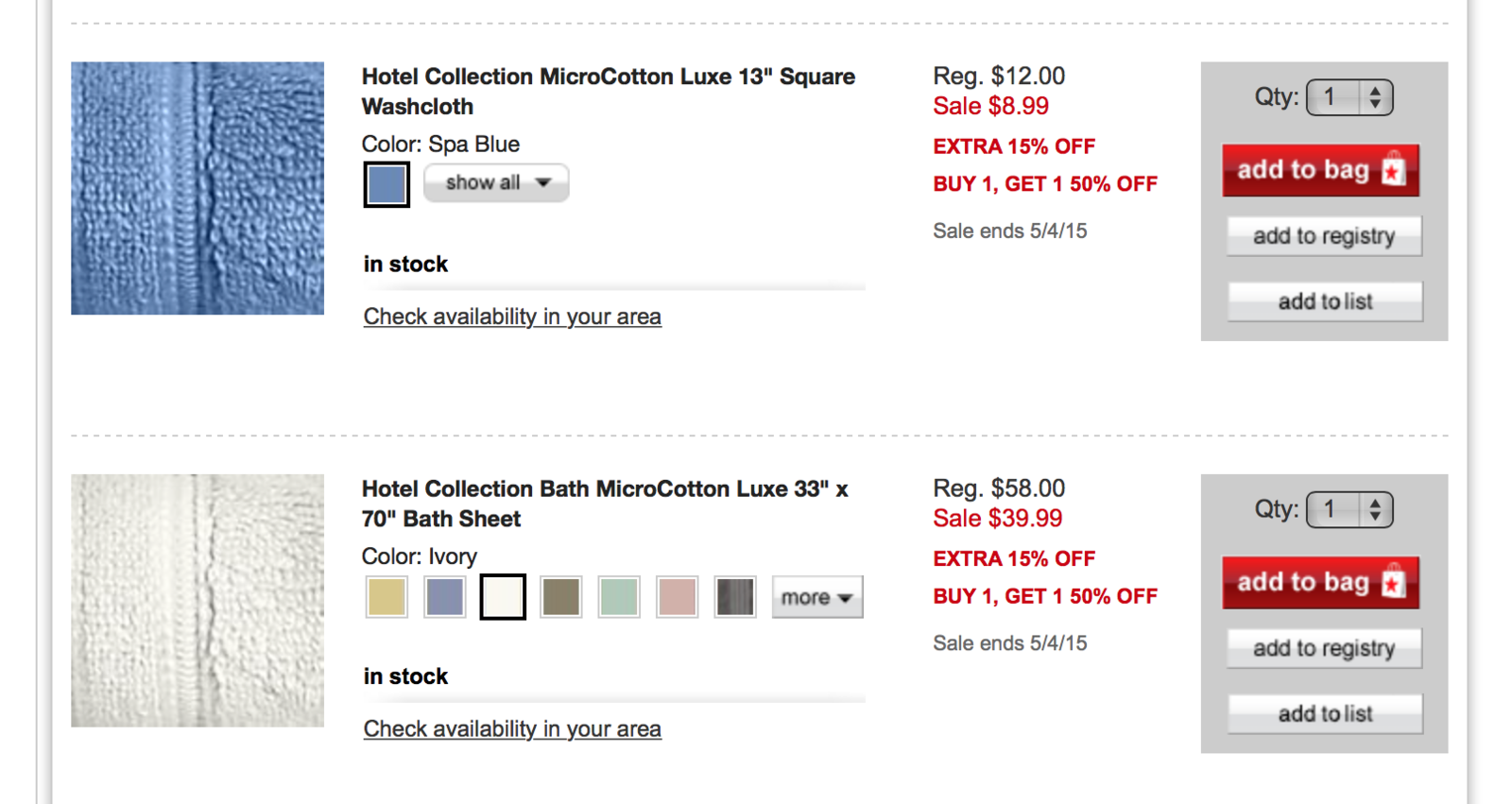
Methods

Frequent itemsets (Association rules)
Collaborative Filtering:
- Item-to-Item (item-based)
- user-to-user (user-based)

Frequent itemsets (assocation rules)

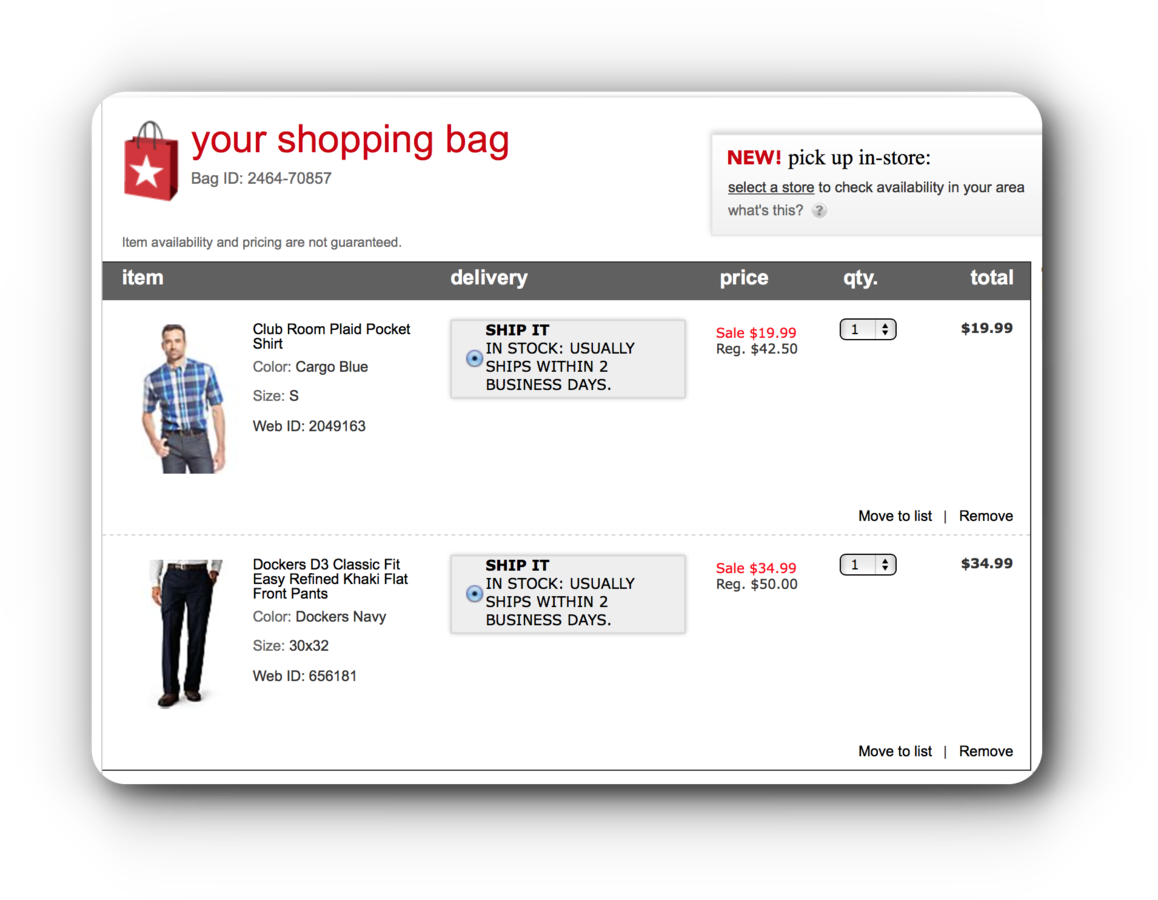
Intuitively, a set of items that appears in many baskets is said to be “frequent”

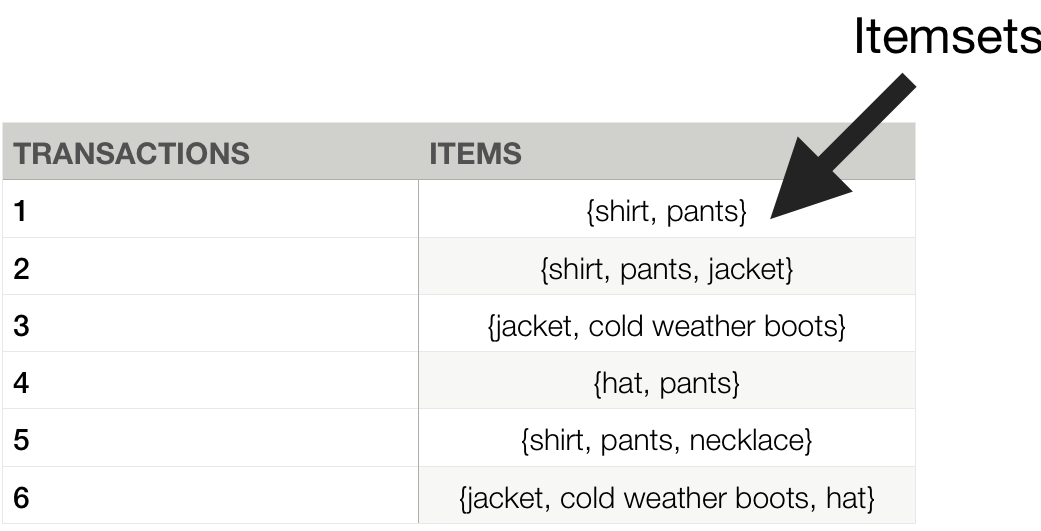
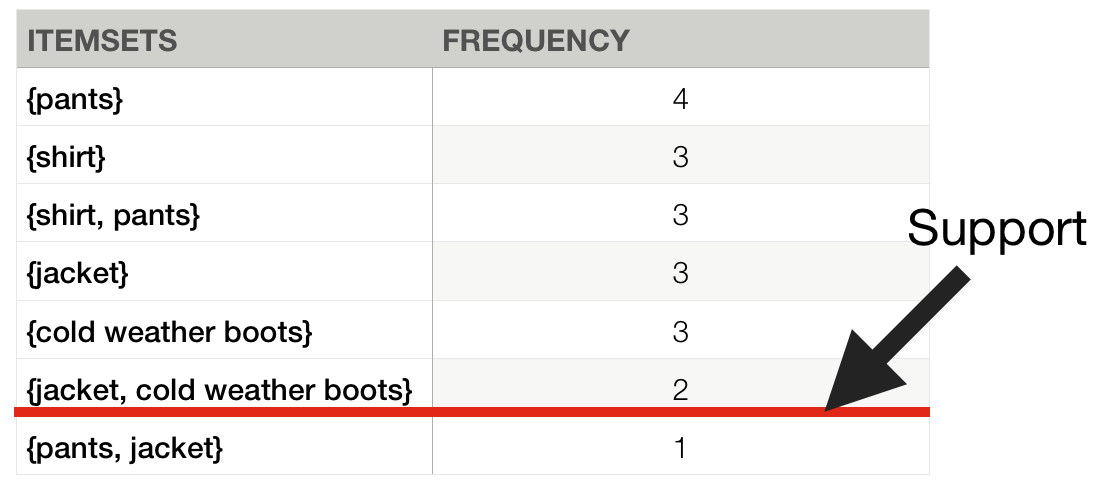
Association rules

{shirt} → pants

{pants} → shirt

{jacket} → cold weather boots

{cold weather boots} → jacket

Is everything OK?

Confidence

Is everything OK?

Confidence = 0.1

NOTE: don't be confused. {shirt}, {pants} aren't categories they are UPSs

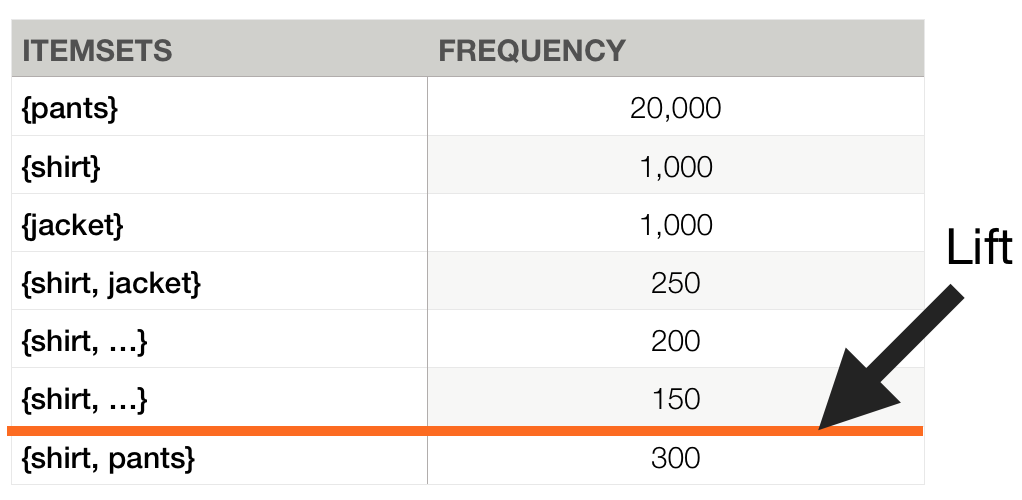
Lift

Transactions count = 100,000

Lift({shirt, jacket}) = 25

Lift({shirt, pants}) = 1.5
We're looking for Lift > 1.0 but it's better to have Lift > 2.0
just for sure

So what do we want?

1. We want do find frequent itemsets.

2. For found itemsets we'd like to build most frequent associations

3. We'd like to find not just statistically probable

Formalism

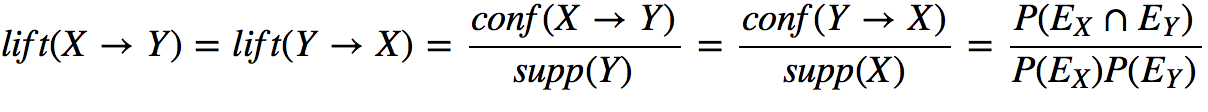
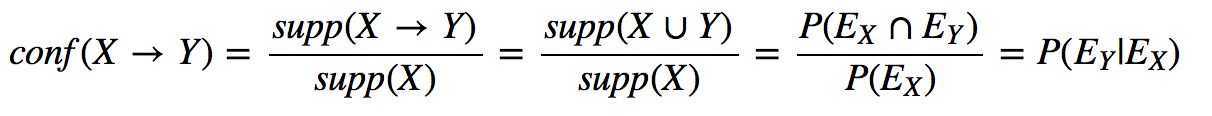
Complexity analysis

Let transaction size be = n

Max itemset cardinality = k

Combination:

k <= 3

Complexity analysis. Examples

Transaction (4) = {t-shirt, shirt, pants, coat}

= 4

= 6

= 4

Transaction (10) = {t-shirt, shirt, pants, coat, jacket, ....}

= 10

= 45

= 10

Overall itemsets count: 14

Overall itemsets count: 65

Transaction (100) = {....}

Overall itemsets count: 5150

Transactions count = 100,000,000 | itemsets count:

100,000,000 * 50 = 5,000,000,000 itemsets

Algorithms

Apriori algorithm - just classic

ParEclat algorithm - parallel, used in R (Eclat), package: "arules"

Parallel FP-growth algorithm - applicable for BigData. Used in Mahout. Based on FP-tree

Top-K (Non Redundant) Association Rules - applicable for real big data. It is used by Predictiveworks for their solution which is based on Spark, named (spark-arules).

Collaborative Filtering

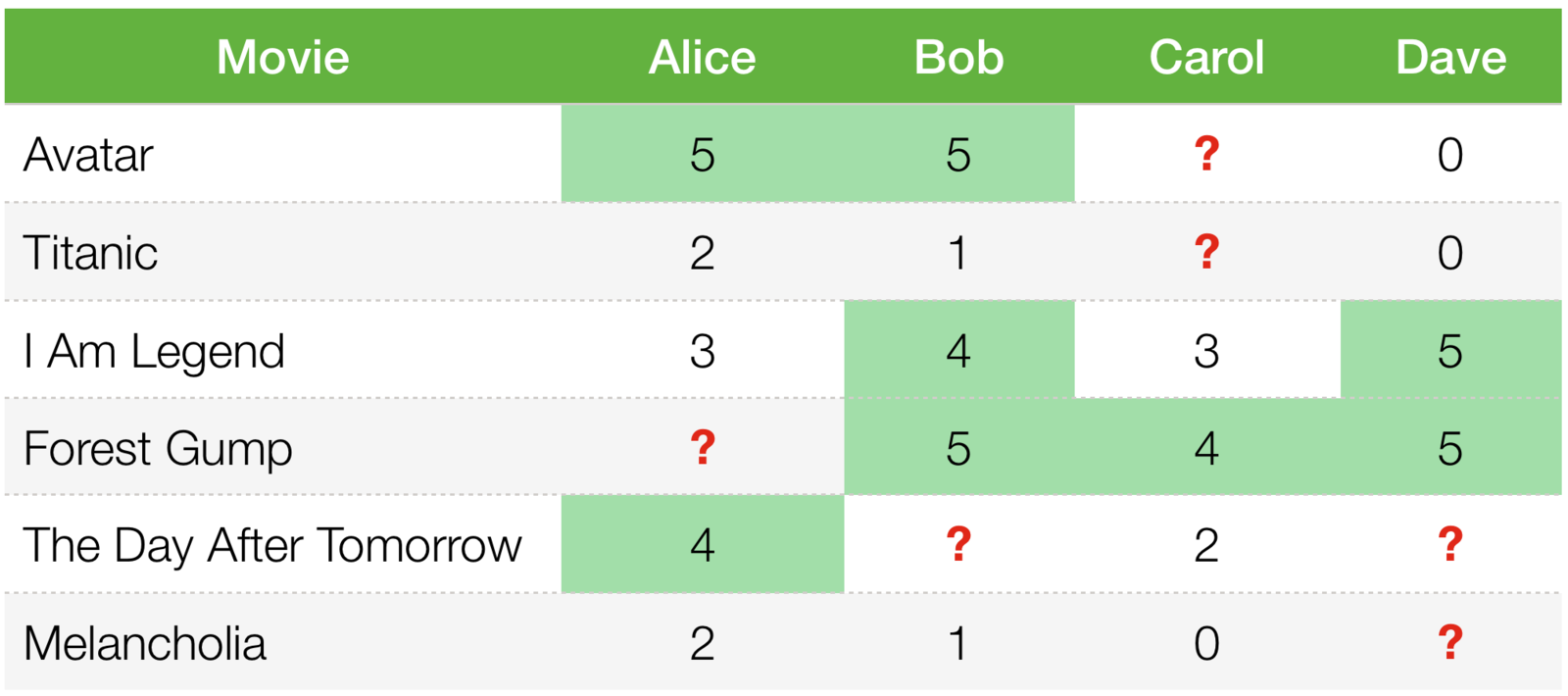
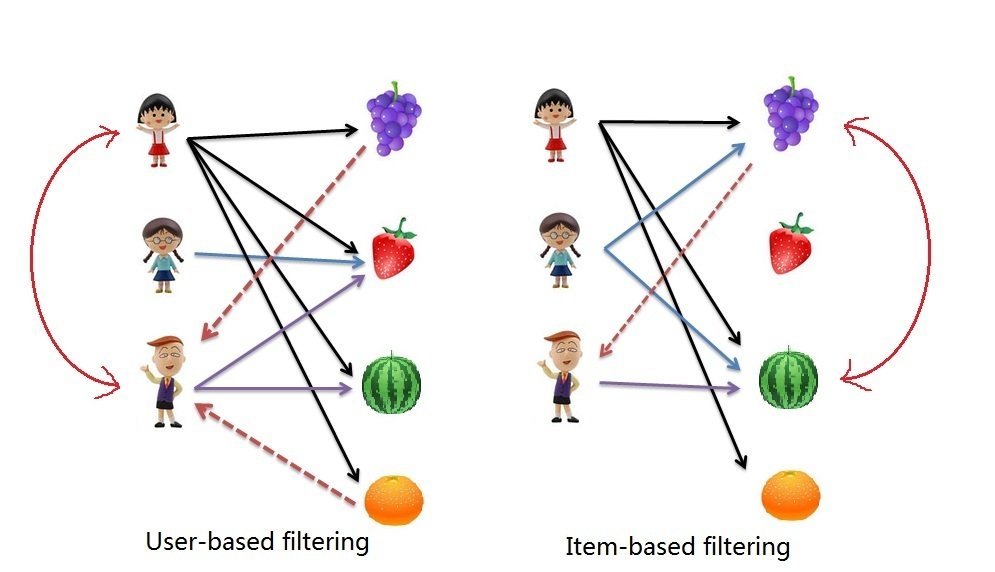
What an idea!

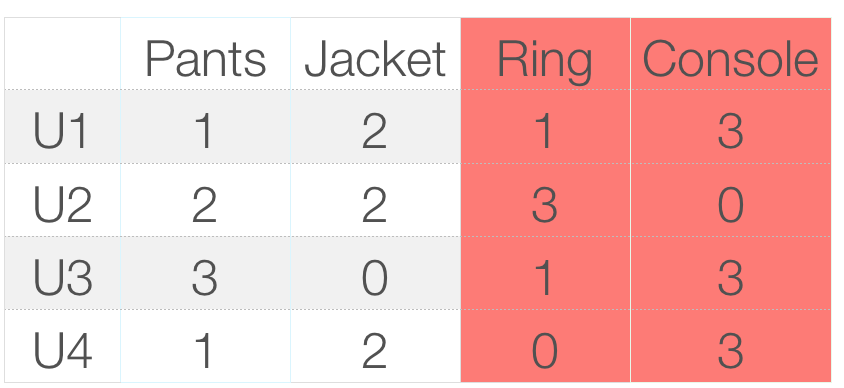
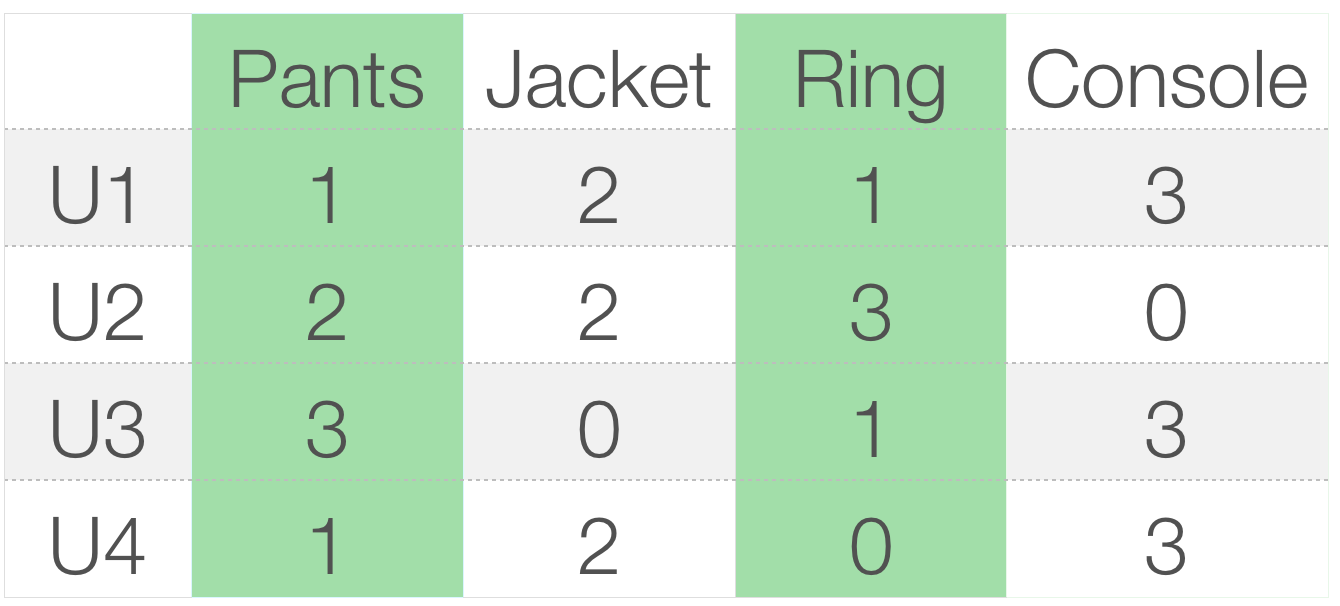
User’s purchases and rates items

Which is better?

What's a problem with user-based collaborative filtering?

Computationally expensive. It is O(MN) in the worst case

... But it can be reduced approximately to O(M + N). Still it's

"Even so, for very large data sets — such as 10 million or more customers and 1 million or more catalog items — the algorithm encounters severe performance and scaling issues."

Is it reasonable?

We could build a product-to-product matrix by iterating through all item pairs and computing a similarity metric for each pair.

Similarity types:

Cosine

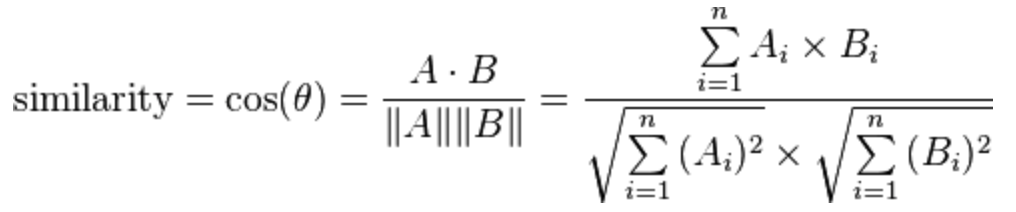
Jaccard similarity

Pearson (correlation)-based similarity

...

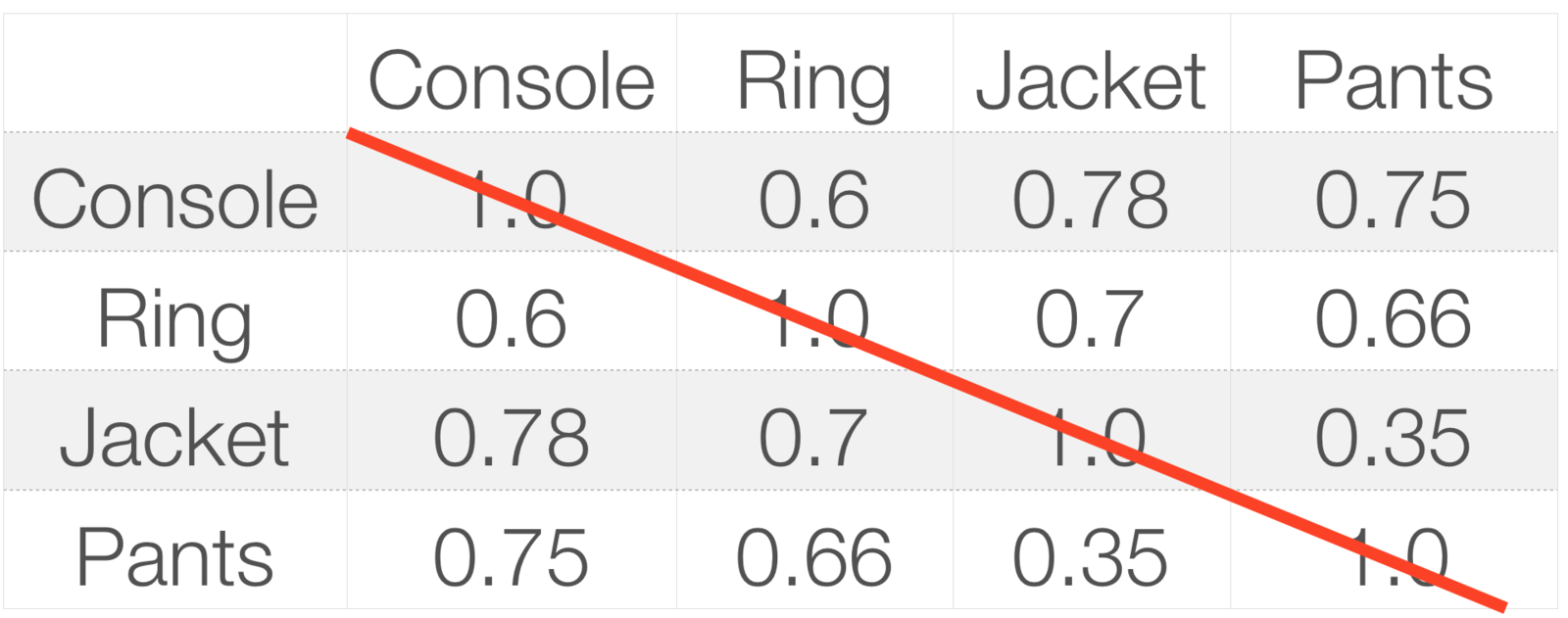
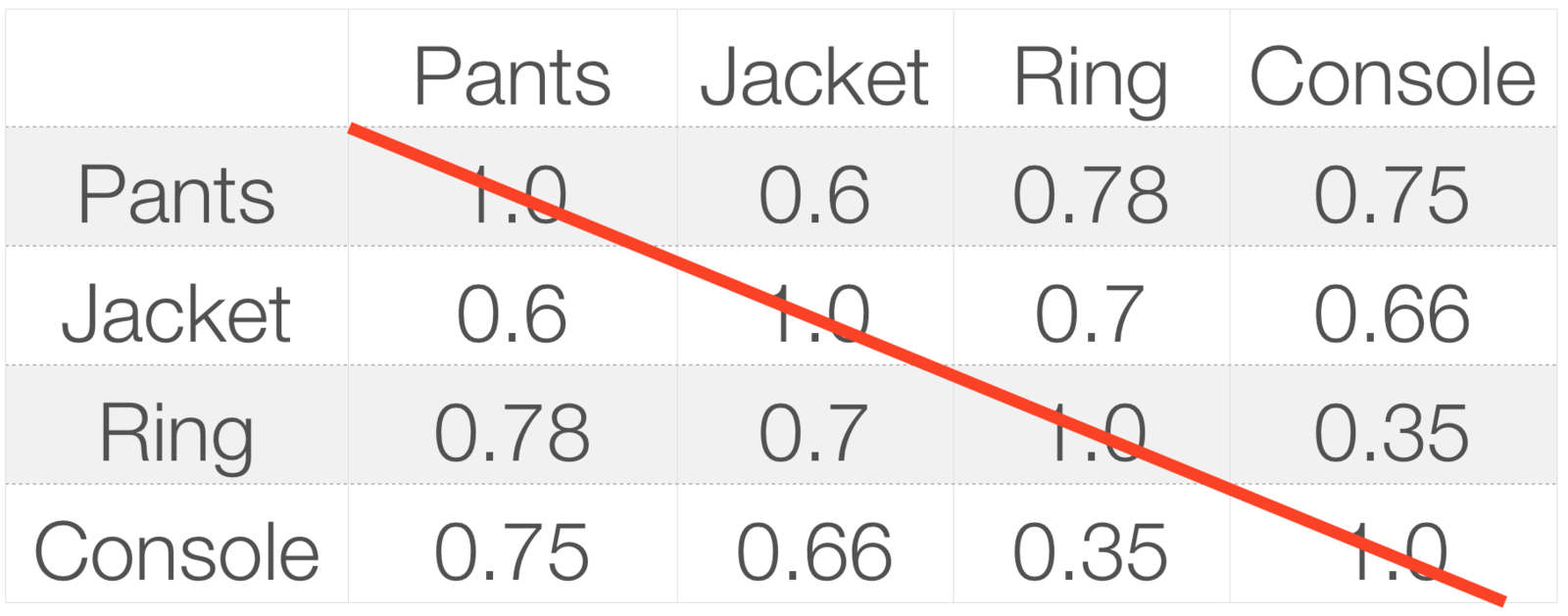
Example

L2norm(A)

A, B = A'

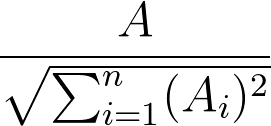
L2norm(A) * L2norm(A)' =

Data Mining

Wikipedia: is the computational process of discovering patterns in large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics, and database systems.

Using

Having

and

Discover

project "Celestial Mechanics" by colleagues Scott Hessels and Gabriel Dunne at UCLA

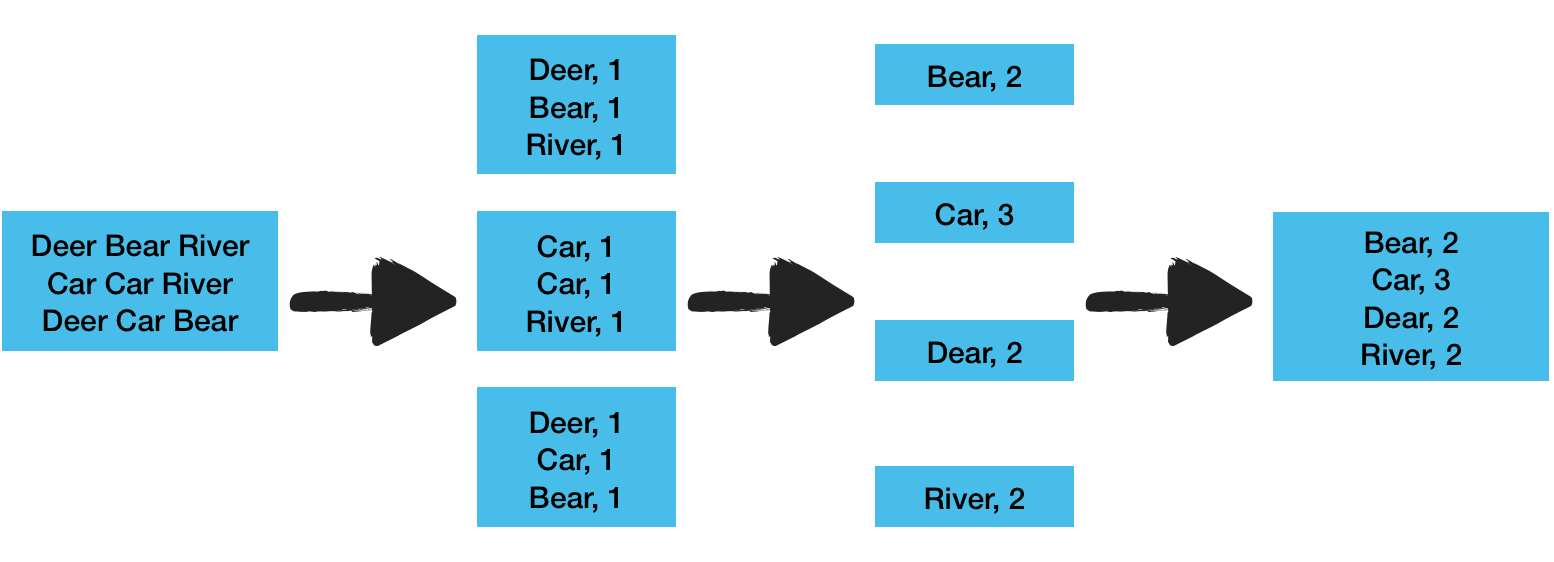
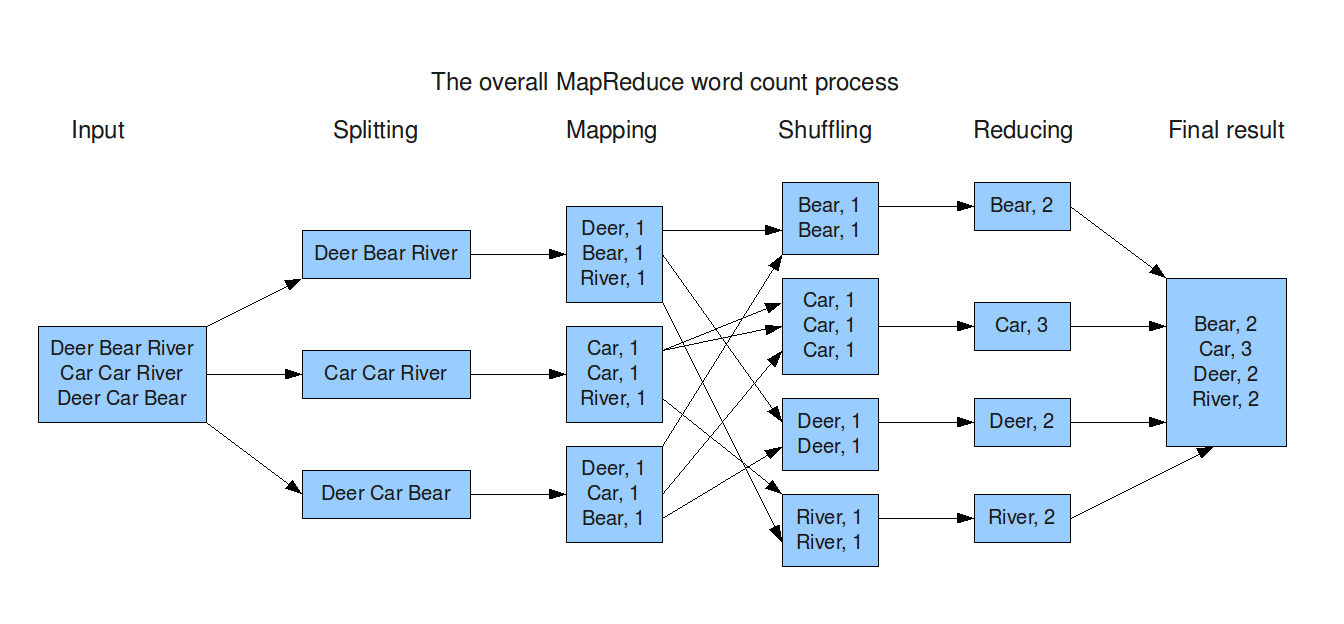
MapReduce

Input

Mapping

Reducing

Result

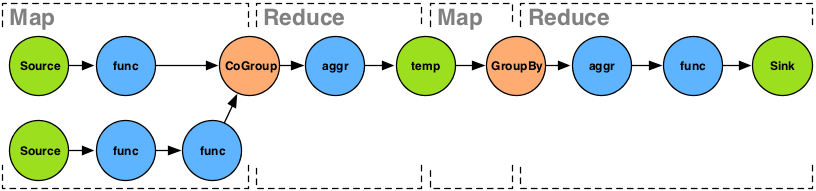
MapReduce Algorithms

1. Page Rank

2. Matrix-Matrix/Vector Multiplication

3. Grouping and Aggregation

4. Union, Intersection, and Difference

etc.

Examples

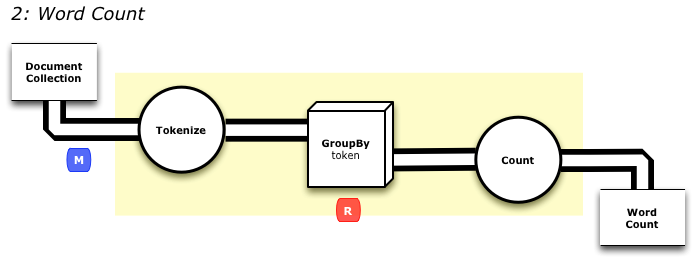
class WordCountJob(args: Args) extends Job(args) {
  TypedPipe.from(TextLine(args("input")))
    .flatMap { line => tokenize(line) }
    .groupBy { word => word } // use each word for a key
    .size // in each group, get the size
    .write(TypedTsv[(String, Long)](args("output")))

  // Split a piece of text into individual words.
  def tokenize(text : String) : Array[String] = {
    // Lowercase each word and remove punctuation.
    text.toLowerCase.replaceAll("[^a-zA-Z0-9\\s]", "").split("\\s+")
  }
}

kiji-modeling

kiji-scoring

org.kiji.modeling.lib.RecommendationPipe

kiji-modeling

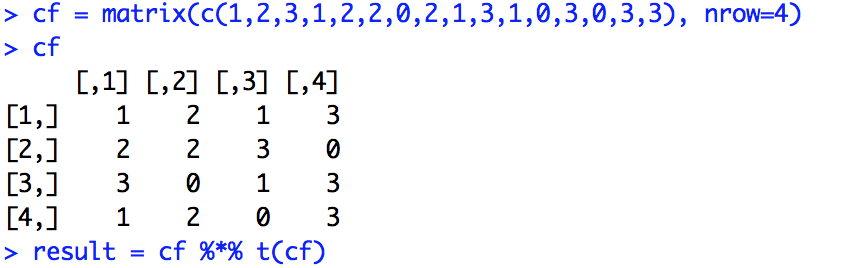
def cosineSimilarity[R <% Ordered[R], C <% Ordered[C]](fieldSpec: (Fields, Fields)): Pipe = {

    // Convert pipe into a matrix with rows for users and columns for items
    val userRatingsMatrix: Matrix[R, C, Double] =
        pipeToUserItemMatrix[R, C](fieldSpec._1)

    val preparedMatrix = userRatingsMatrix
      .transpose
      .rowL2Normalize
      .transpose

    val similarityMatrix = (preparedMatrix.transpose * preparedMatrix)

    similarityMatrixToPipe[C](fieldSpec._2, similarityMatrix)
}

com.twitter.scalding.mathematics.Matrix

com.twitter.scalding.mathematics.RowVector

Bla Bla Cluster Diagram

(proprietary information)

!!!FOR NERDS ONLY!!!

Mahout Examples

mahout recommenditembased -s SIMILARITY_COSINE -i /path/to/input/file 
    -o /path/to/desired/output --numRecommendations 25

/path/to/input/file should contain userID, itemID and preference



DataModel model = new FileDataModel(new File("data.txt"));
...
// Construct the list of pre-computed correlations
Collection<GenericItemSimilarity.ItemItemSimilarity> correlations = ...;
ItemSimilarity itemSimilarity = new GenericItemSimilarity(correlations);
...
Recommender recommender = new GenericItemBasedRecommender(model, itemSimilarity);
Recommender cachingRecommender = new CachingRecommender(recommender);
...
List<RecommendedItem> recommendations = cachingRecommender.recommend(1234, 10);

Console based:

Java based:

R Examples

R. The Eclat Algorithm

Hadoop. MapReduce



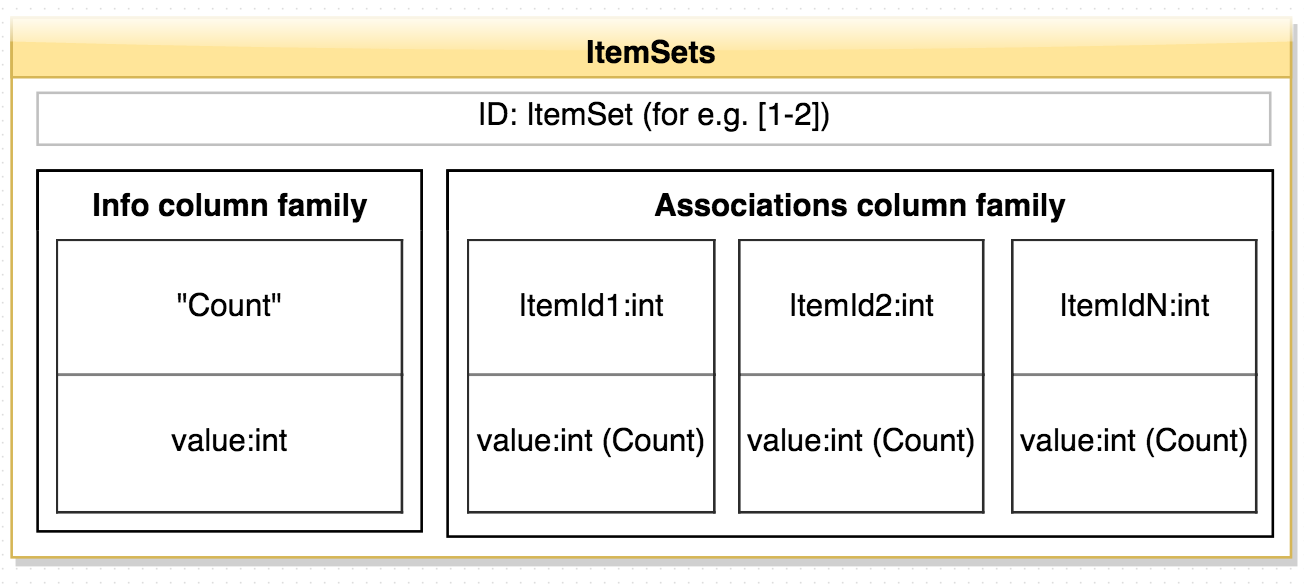
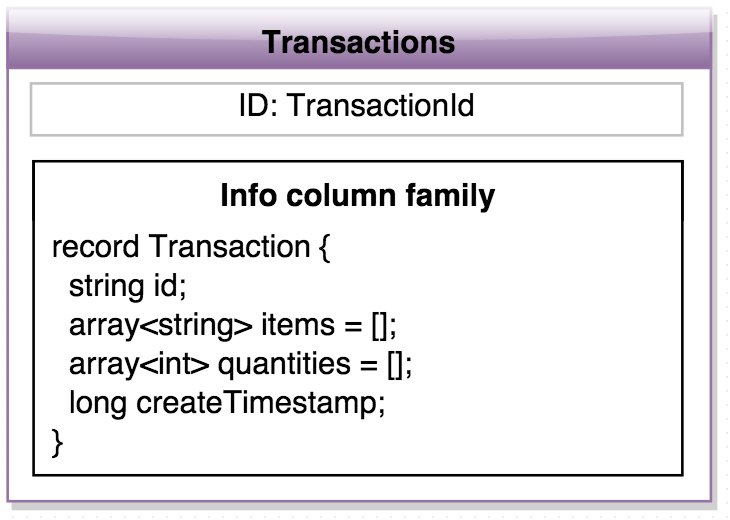
public class AssociationsMapper extends TableMapper<ImmutableBytesWritable, Association> {

    public void map(ImmutableBytesWritable row, Result value, Context context) throws ... {
        Transaction transaction = Avro.bytesToTransaction(value.getValue(INFO_FAM, ITEMS_COLUMN));

        Collection<ItemSetAndAssociation<String>> itemSetAndAssociations = itemSetsGenerator
                .generateItemSetsAndAssociations(transaction.getItems(), 1);

        context.getCounter(COUNTER).increment(itemSetAndAssociations.size());
        for (ItemSetAndAssociation<String> itemSetAndAssociation : itemSetAndAssociations) {
            for (Map.Entry<String, Long> association : 
					itemSetAndAssociation.getAssociationMap().entrySet()) {
                ...
                itemSetCount = itemSetAndAssociation.getCount();
				...
                context.write(toBytesWritable(itemSetAndAssociation.getItemSet()),
                        new Association(itemSetCount, association.getKey(), association.getValue()));
                context.getCounter(Counters.ASSOCIATIONS).increment(1);
            }
            ...
        }
        context.getCounter(Counters.ROWS).increment(1);
    }
}

Mapper



public class AssociationsReducer extends TableReducer<ImmutableBytesWritable, Association, 
    ImmutableBytesWritable> {

    @Override
    public void reduce(ImmutableBytesWritable key, Iterable<Association> values, Context context)
            throws IOException, InterruptedException {
        Put put = new Put(key.get());
        long itemSetCount = 0;

        Map<String, AtomicLong> associationsMap = new HashMap<>();
        for (Association value : values) {
            itemSetCount += value.getItemSetCount();
            ...
            associationsMap.putIfAbsent(value.getAssociationId(), new AtomicLong(0l));
            associationsMap.get(value.getAssociationId()).addAndGet(value.getAssociationCount());
        }
        for (Map.Entry<String, AtomicLong> entry : associationsMap.entrySet()) {
            put.add(ASSOCIATION_FAM, toBytes(entry.getKey()), toBytes(entry.getValue().get()));
        }
        put.add(COUNT_FAM, COUNT_COL, toBytes(itemSetCount));
        context.write(key, put);
    }
}