Causal Dynamical Triangulations with CGAL

Adam Getchell

acgetchell@ucdavis.edu

University of California, Davis

C++Now 2016

Causal Dynamical Triangulations

A candidate theory of quantum gravity

(Not             )

10^{100}
1010010^{100}

Why is this hard?

(In English)

Everything else is simpler at short distances.

 

 

 

 

Time

Space

Credit: Wikipedia

Why is this hard?

(In English)

Everything else is simpler at short distances.

 

Gravity is more complicated.

  • No local observables
    • Mass is really only defined at the horizon
    • Energy is not conserved
  • Time is a problem
    • No universal clock
    • Closed timelike curves possible

And a bunch of other highly entertaining issues ...

Does CDT have a Newtonian Limit?

CDT looks like GR at cosmological scales, does it have a Newtonian limit?

F=G_{N}\frac{m_{1}m_{2}}{r^2}
F=GNm1m2r2F=G_{N}\frac{m_{1}m_{2}}{r^2}

At first glance, this is hard:

  • CDT is not well-suited for approximating smooth classical space-times
  • We don't have the time or resolution to watch objects fall

Path Integral

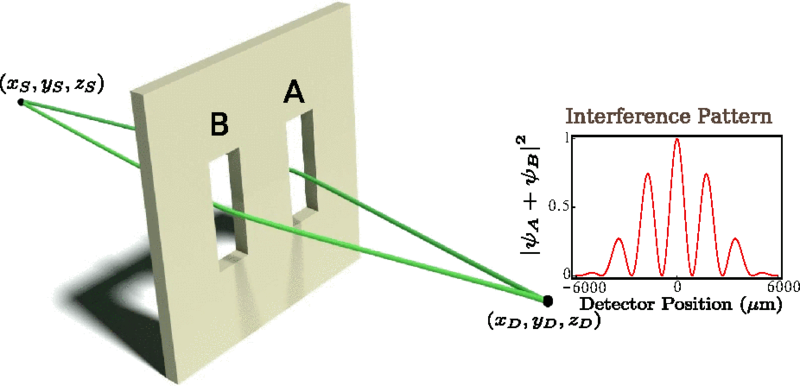
Path Integral

\langle B|T|A\rangle=\int\mathcal{D}[g]e^{iS_{EH}}
⟨B∣T∣A⟩=∫D[g]eiSEH\langle B|T|A\rangle=\int\mathcal{D}[g]e^{iS_{EH}}
S_{EH}=\frac{1}{16\pi G_{N}}\int d^{4}x\sqrt{-g}(R-2\Lambda)
SEH=116πGN∫d4x−g(R−2Λ) S_{EH}=\frac{1}{16\pi G_{N}}\int d^{4}x\sqrt{-g}(R-2\Lambda)

Equations of Motion

\partial S = 0 \rightarrow R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}
∂S=0→Rμν−12Rgμν=8πGNTμν\partial S = 0 \rightarrow R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}

Ricci scalar

Cosmological constant

Ricci tensor

Ricci scalar

Stress-Energy tensor

Transition probability amplitude

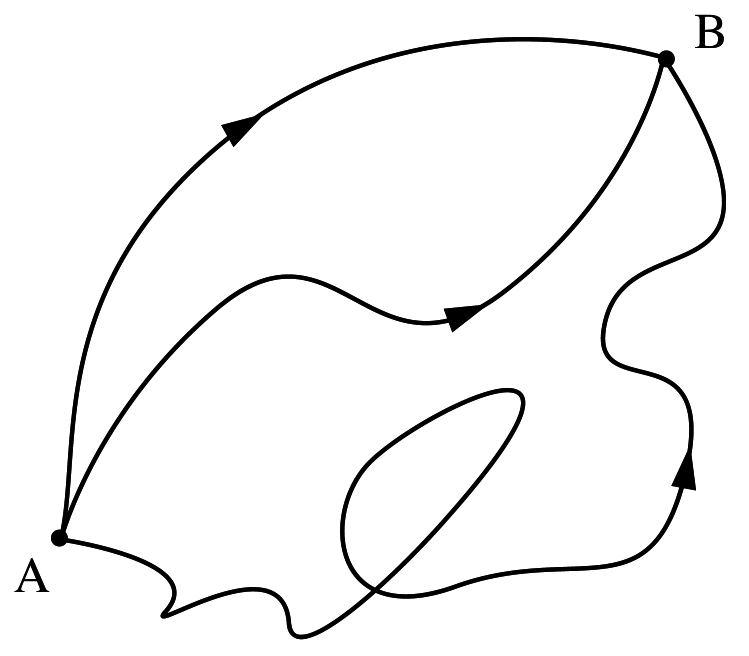
Calculating the Path Integral

Quickly gets complicated!

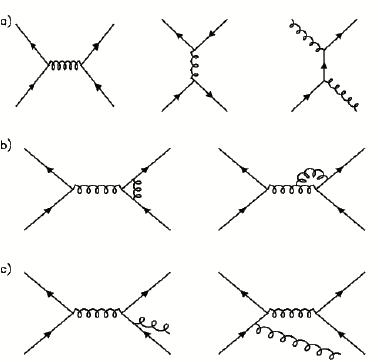
Background

R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}
Rμν−12Rgμν=8πGNTμνR_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}

Parallel Transport

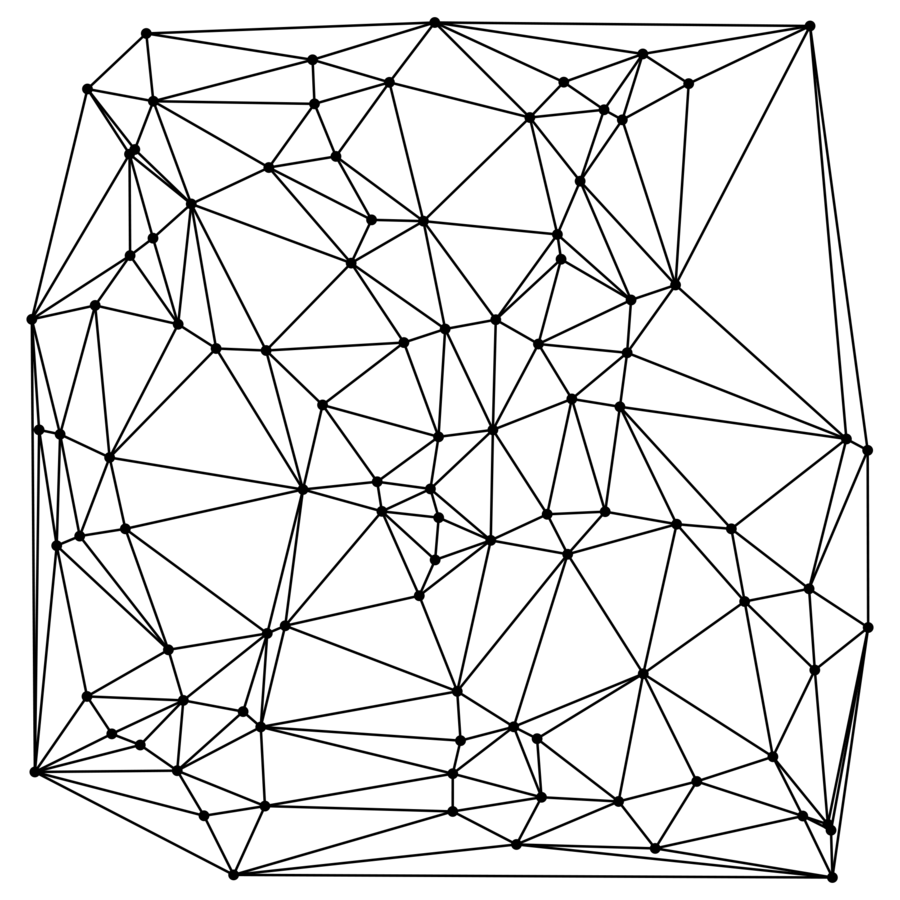
DT Path Integral

\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{iS_{R}(T)}
⟨B∣T∣A⟩=∑triangulations1C(T)eiSR(T)\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{iS_{R}(T)}
S_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)
SR=18πGN(∑hingesAhδh−Λ∑simplicesVs)S_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)

Inequivalent Triangulations

Regge Action

Partition Function

Transition probability amplitude

Now What?

Foliation

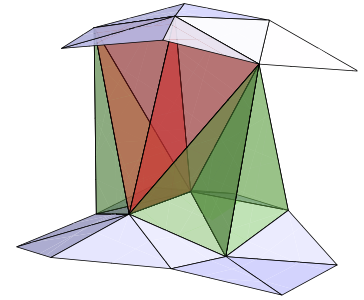
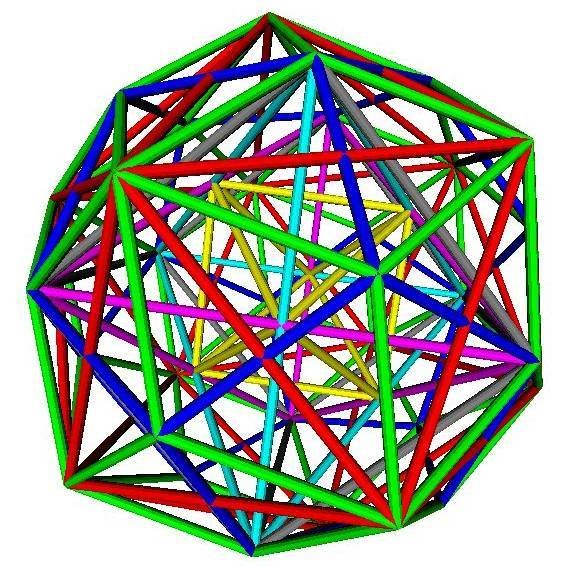
CDT Path Integral

\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{iS_{R}(T)}
⟨B∣T∣A⟩=∑triangulations1C(T)eiSR(T)\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{iS_{R}(T)}

CDT Path Integral

\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-S_{R}(T)}
⟨B∣T∣A⟩=∑triangulations1C(T)e−SR(T)\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-S_{R}(T)}

Wick rotation

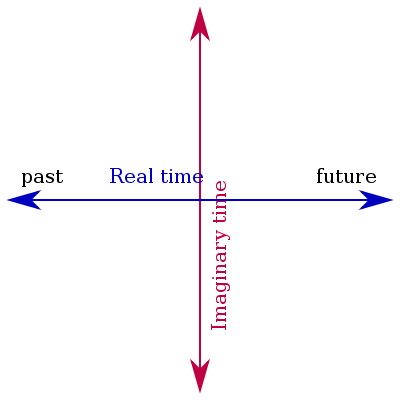
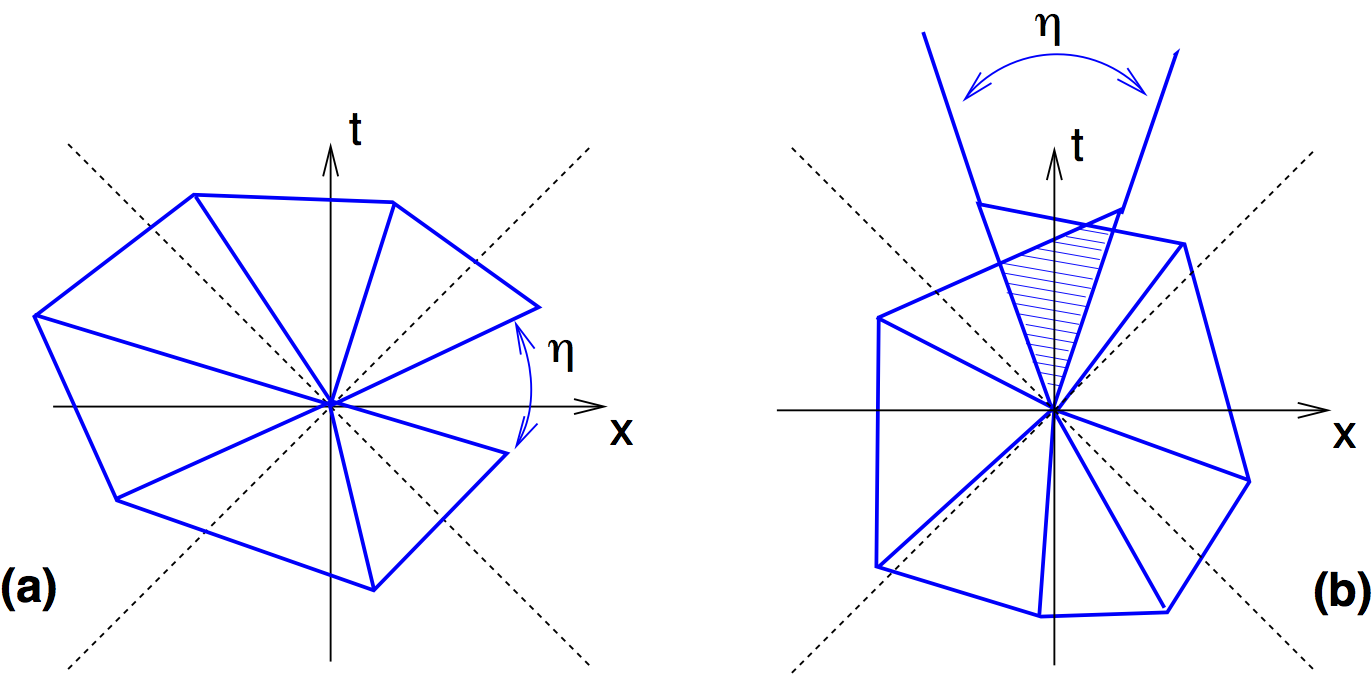
What is an inequivalent triangulation?

3D Ergodic Moves

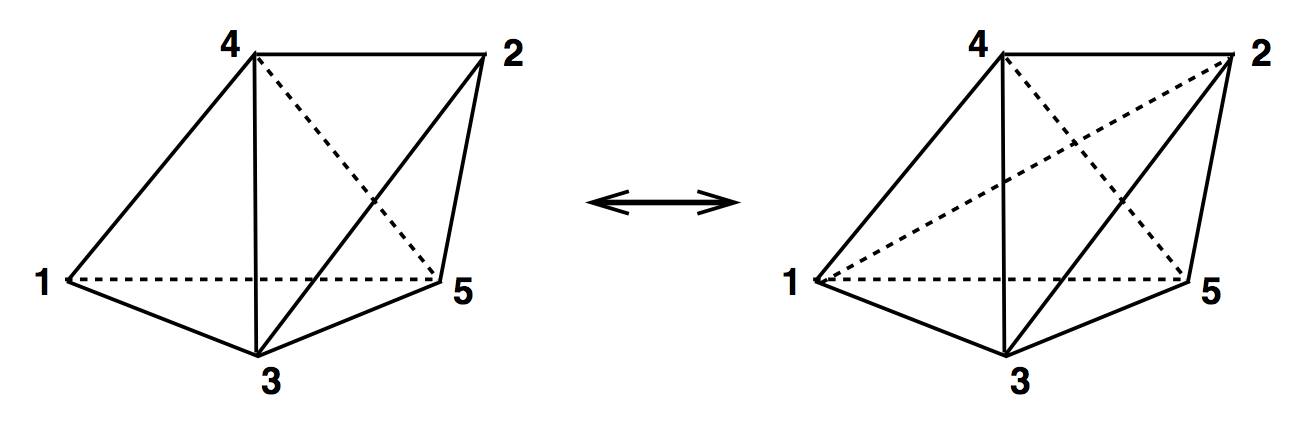
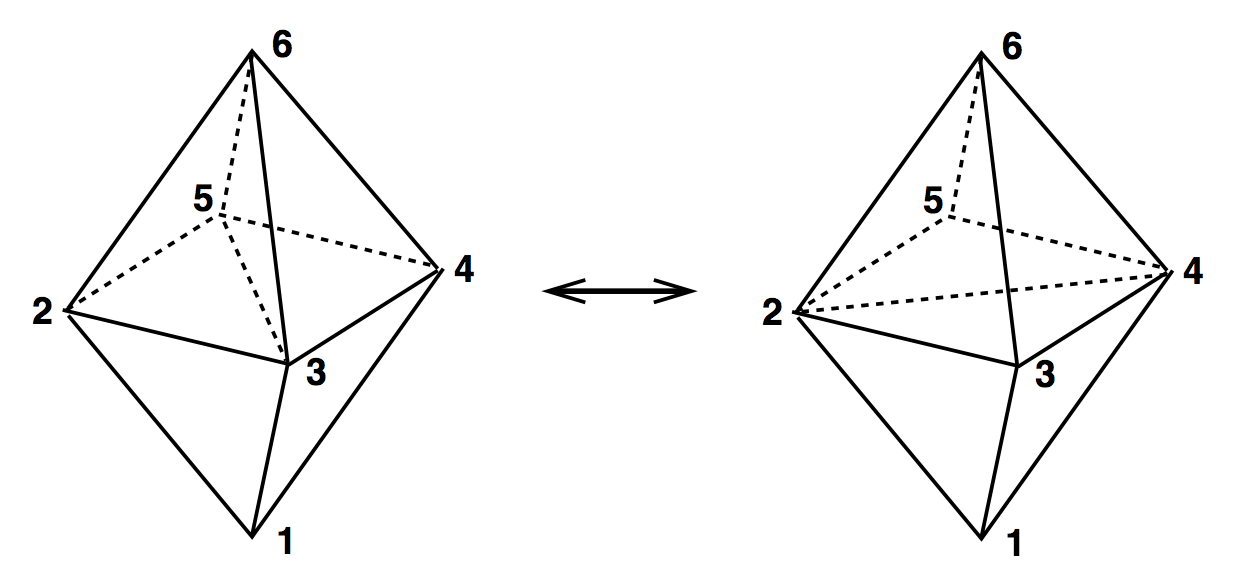
(2,3) & (3,2)

(4,4)

(2,6) & (6,2)

Simplices involved

Move name

(3,1) & (2,2)

2 (1,3) & 2 (3,1)

(1,3) & (3,1)

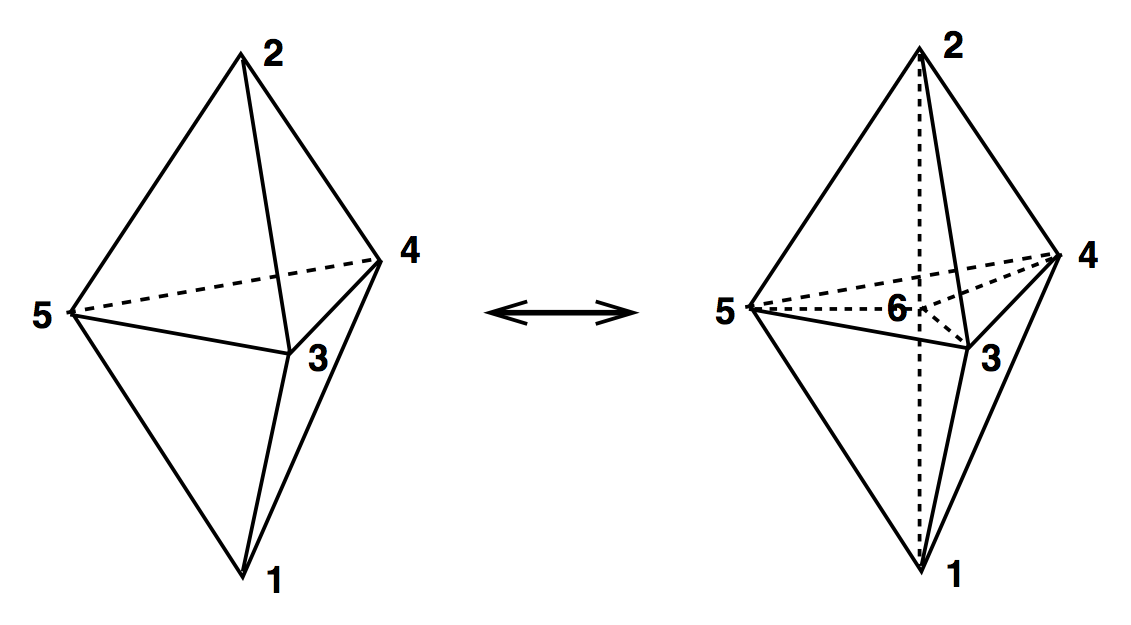
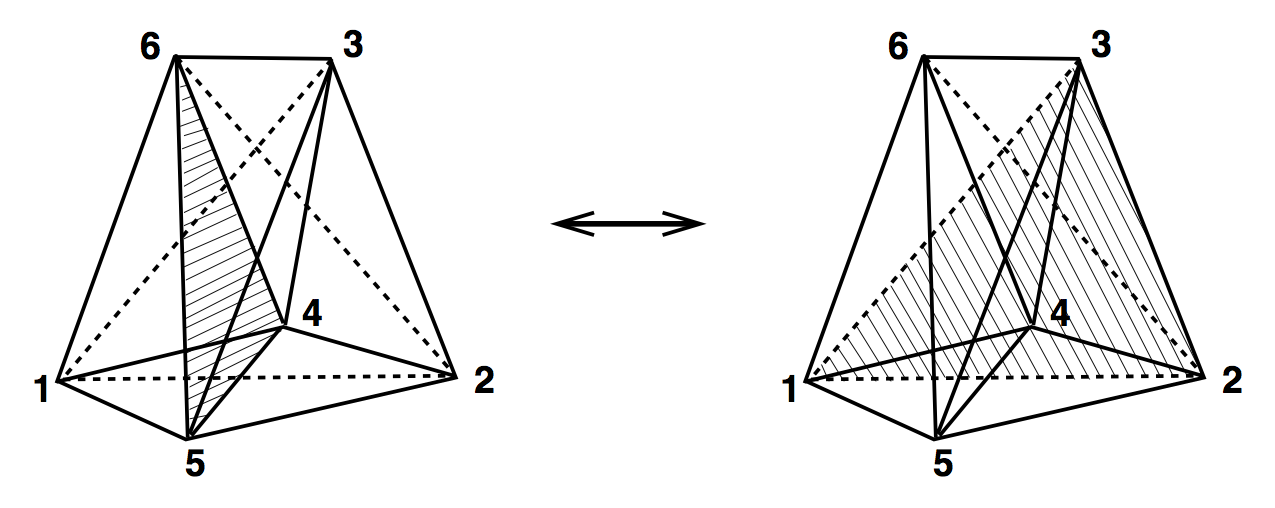
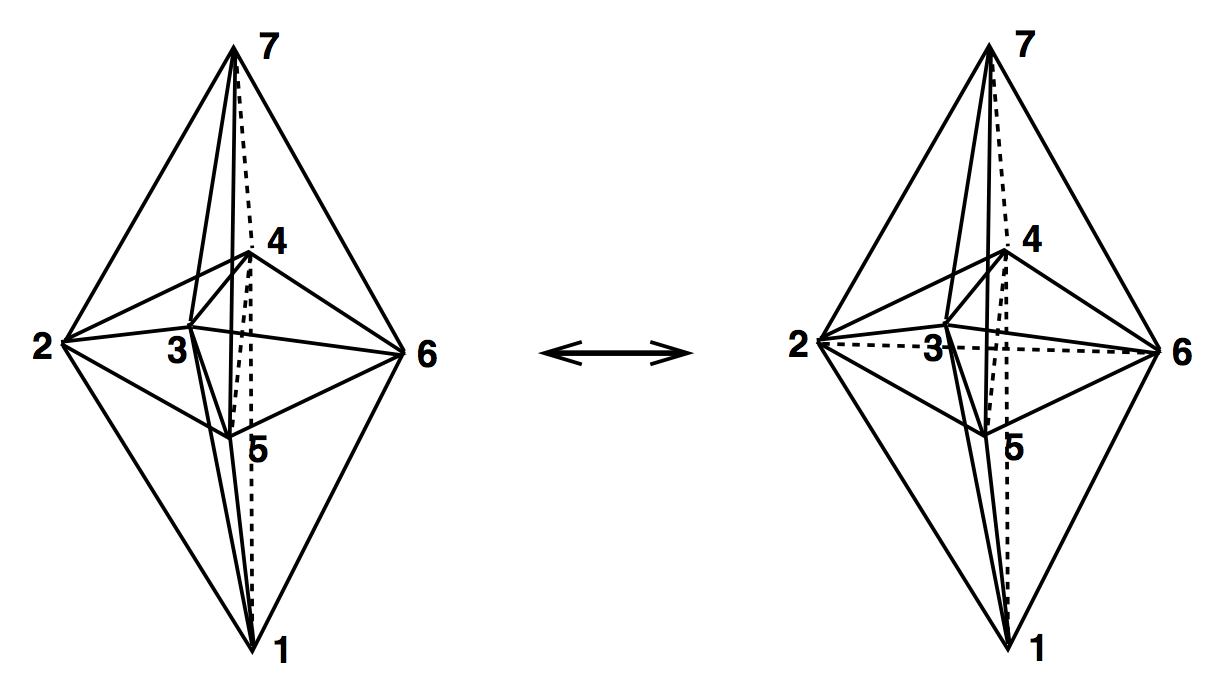
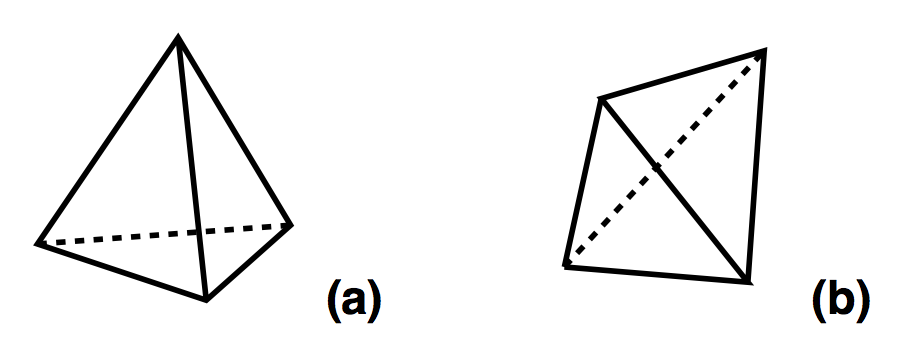
4D Ergodic Moves

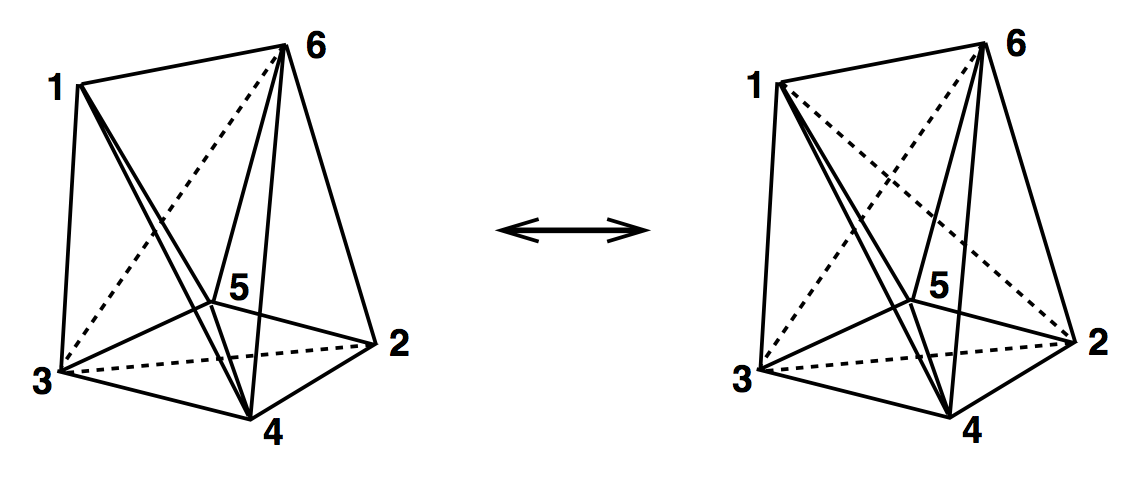
(2,4) & (4,2)

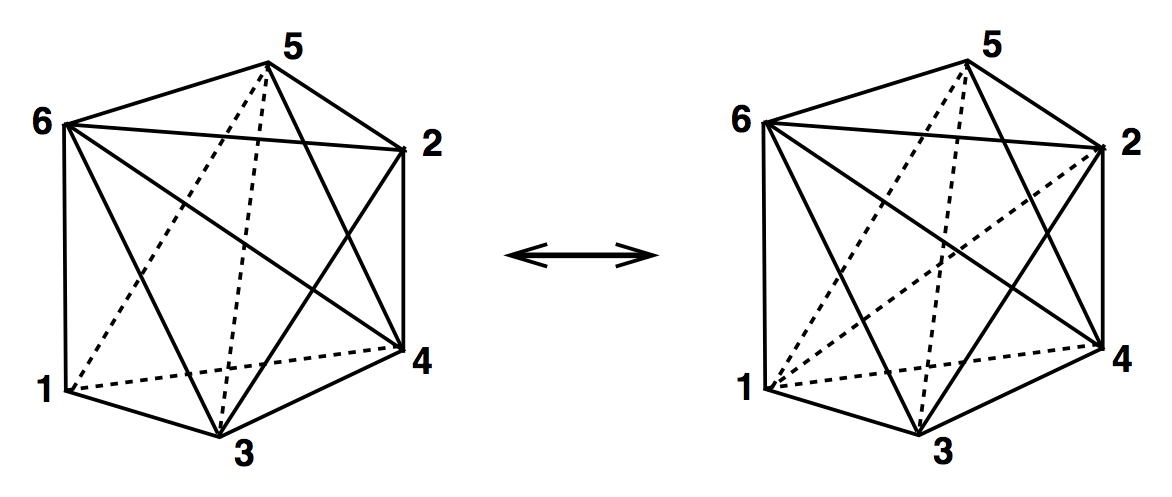
(3,3)

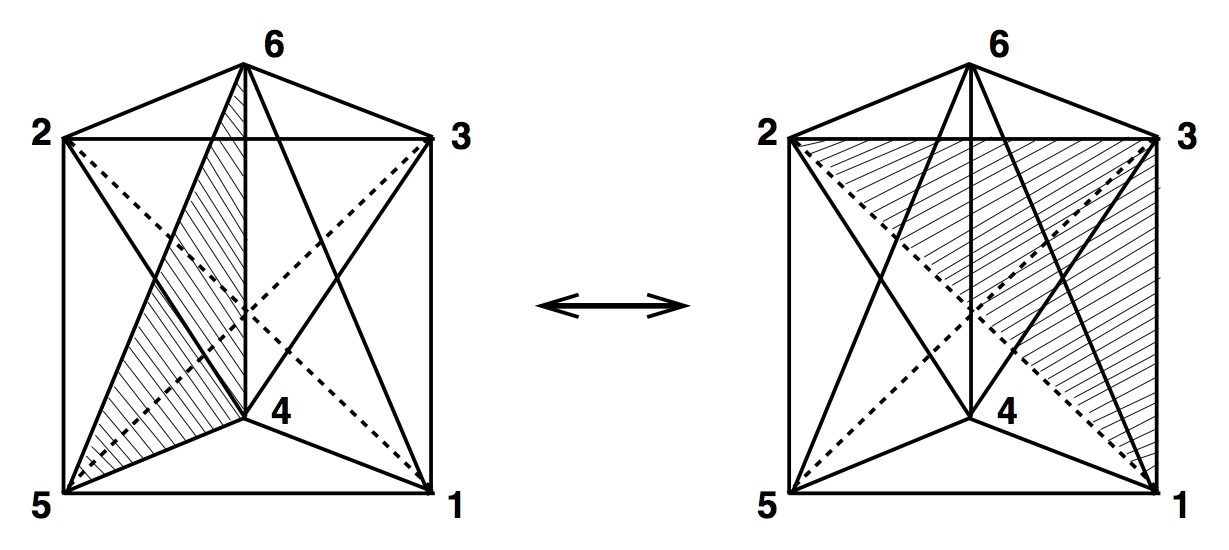
(4,6) & (6,4)

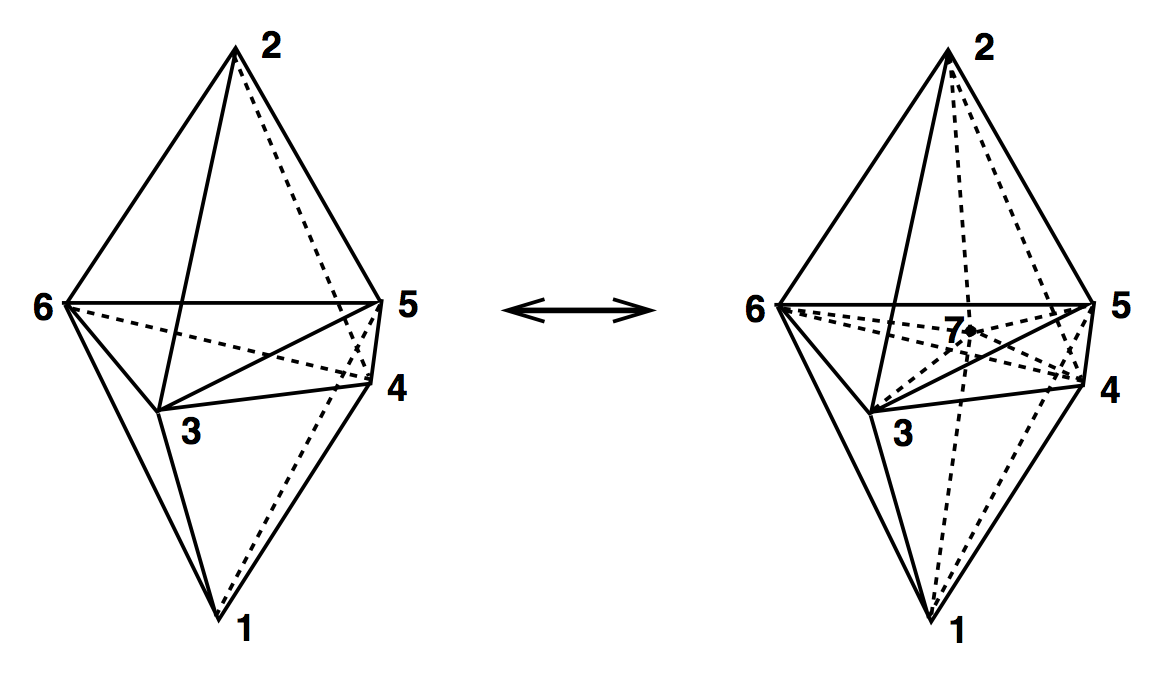
(2,8) & (8,2)

Metropolis-Hastings

\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-S_{R}(T)}
⟨B∣T∣A⟩=∑triangulations1C(T)e−SR(T)\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-S_{R}(T)}

Inequivalent Triangulations

Partition Function

Wick rotation

  1. Pick an ergodic (Pachner) move
  2. Make that move with a probability of a1a2, where:
a_{1}=\frac{move[i]}{\sum\limits_{i}move[i]}
a1=move[i]∑imove[i]a_{1}=\frac{move[i]}{\sum\limits_{i}move[i]}
a_{2}=e^{\Delta S}
a2=eΔSa_{2}=e^{\Delta S}

CDT Action

\begin{array}{l} S^{(3)} &=& 2\pi k\sqrt{\alpha}N_1^{TL} \\ &+& N_3^{(3,1)}\left[-3k\text{arcsinh}\left(\frac{1}{\sqrt{3} \sqrt{4\alpha +1}}\right)-3k\sqrt{\alpha}\text{arccos}\left(\frac{2\alpha+1} {4\alpha+1}\right)-\frac{\lambda}{12}\sqrt{3\alpha+1}\right] \\ &+& N_3^{(2,2)}\left[2k\text{arcsinh}\left(\frac{2\sqrt{2}\sqrt{2\alpha+1}} {4\alpha +1}\right)-4k\sqrt{\alpha}\text{arccos}\left(\frac{-1}{4\alpha+1} \right)-\frac{\lambda}{12}\sqrt{4\alpha +2}\right] \end{array}
S(3)=2πkαN1TL+N3(3,1)[−3karcsinh(134α+1)−3kαarccos(2α+14α+1)−λ123α+1]+N3(2,2)[2karcsinh(222α+14α+1)−4kαarccos(−14α+1)−λ124α+2]\begin{array}{l} S^{(3)} &=& 2\pi k\sqrt{\alpha}N_1^{TL} \\ &+& N_3^{(3,1)}\left[-3k\text{arcsinh}\left(\frac{1}{\sqrt{3} \sqrt{4\alpha +1}}\right)-3k\sqrt{\alpha}\text{arccos}\left(\frac{2\alpha+1} {4\alpha+1}\right)-\frac{\lambda}{12}\sqrt{3\alpha+1}\right] \\ &+& N_3^{(2,2)}\left[2k\text{arcsinh}\left(\frac{2\sqrt{2}\sqrt{2\alpha+1}} {4\alpha +1}\right)-4k\sqrt{\alpha}\text{arccos}\left(\frac{-1}{4\alpha+1} \right)-\frac{\lambda}{12}\sqrt{4\alpha +2}\right] \end{array}

3D

CDT Action

4D

\begin{array}{l} S^{(4)}\!\! &=&\!\! \frac{k \pi}{2} \sqrt{4\alpha +1}\ N_{2}^{TL} + N_{4}^{(4,1)}\cdot \\ && \!\!\Biggl( -\sqrt{3} k\ {arcsinh} \frac{1}{2\sqrt{2}\sqrt{3\alpha +1}} -\frac{3 k}{2} \sqrt{4\alpha +1} \arccos\frac{2\alpha +1}{2 (3\alpha +1)} -\lambda \frac{\sqrt{8\alpha +3}}{96} \Biggr) \\ &+&\!\! N_{4}^{(3,2)} \Biggl( \frac{\sqrt{3} k}{4}\ {arcsinh}\frac{\sqrt{3}\sqrt{12 \alpha +7}} {2 (3 \alpha+1)} - \frac{3 k}{4} \sqrt{4\alpha +1}\\ &&\!\!\biggl( 2\arccos\frac{-1}{2\sqrt{2}\sqrt{2\alpha +1}\sqrt{3\alpha +1}} + \arccos\frac{4\alpha +3}{4 (2\alpha +1)}\biggr) -\lambda \frac{\sqrt{12\alpha +7}}{96}\Biggr) \end{array}
S(4)=kπ24α+1 N2TL+N4(4,1)⋅(−3k arcsinh1223α+1−3k24α+1arccos2α+12(3α+1)−λ8α+396)+N4(3,2)(3k4 arcsinh312α+72(3α+1)−3k44α+1(2arccos−1222α+13α+1+arccos4α+34(2α+1))−λ12α+796)\begin{array}{l} S^{(4)}\!\! &=&\!\! \frac{k \pi}{2} \sqrt{4\alpha +1}\ N_{2}^{TL} + N_{4}^{(4,1)}\cdot \\ && \!\!\Biggl( -\sqrt{3} k\ {arcsinh} \frac{1}{2\sqrt{2}\sqrt{3\alpha +1}} -\frac{3 k}{2} \sqrt{4\alpha +1} \arccos\frac{2\alpha +1}{2 (3\alpha +1)} -\lambda \frac{\sqrt{8\alpha +3}}{96} \Biggr) \\ &+&\!\! N_{4}^{(3,2)} \Biggl( \frac{\sqrt{3} k}{4}\ {arcsinh}\frac{\sqrt{3}\sqrt{12 \alpha +7}} {2 (3 \alpha+1)} - \frac{3 k}{4} \sqrt{4\alpha +1}\\ &&\!\!\biggl( 2\arccos\frac{-1}{2\sqrt{2}\sqrt{2\alpha +1}\sqrt{3\alpha +1}} + \arccos\frac{4\alpha +3}{4 (2\alpha +1)}\biggr) -\lambda \frac{\sqrt{12\alpha +7}}{96}\Biggr) \end{array}

CDT, Kommu et. al.

  • First independent confirmation of results
  • Written in Lisp
  • 256 timeslices, 512K simplices about 6 months on an HPC cluster
  • Lots and lots of data files

Does CDT have a Newtonian Limit?

CDT looks like GR at cosmological scales, does it have a Newtonian limit?

F=G_{N}\frac{m_{1}m_{2}}{r^2}
F=GNm1m2r2F=G_{N}\frac{m_{1}m_{2}}{r^2}

At first glance, this is hard:

  • CDT is not well-suited for approximating smooth classical space-times
  • We don't have the time or resolution to watch objects fall

Find the Newtonian Limit, if it exists

  • Test case, no limit in 3D

Re-implement CDT

  • Rewrite in modern C++
  • Use well-known libraries

Use current tools

Easy to evaluate, use, and contribute

Fast foliated Delaunay Triangulations in CGAL

Fast foliated Delaunay Triangulations in CGAL

256 timeslices, 222,132 vertices,  2,873,253 faces, 1,436,257 simplices

Creation time: 284.596s

(MacBook Pro Retina, Mid 2012)

Remaining Work

  • 4D Ergodic moves
  • Restore Delaunay triangulation after moves(?)
  • HDF5 format data output
  • Improve Visualization pipeline
  • Build data analysis pipeline
  • Parallelize (RaftLib, etc.)
  • Containerize (Docker, etc.)

Interested? Please Join!

Thank You!

[1] The CGAL Project. CGAL User and Reference Manual. CGAL Editorial Board, 4.6.3 edition, 2015.

 

[2] Steve Carlip. Why Quantum Gravity is Hard. Conceptual and Technical Challenges for Quantum Gravity, Rome, September 2014.

 

[3] J. Ambjorn, J. Jurkiewicz, and R. Loll. “Dynamically Triangulating Lorentzian Quantum Gravity.” Nuclear Physics B 610, no. 2001 (May 27, 2001): 347–82.

 

[4] Rajesh Kommu. “A Validation of Causal Dynamical Triangulations.” arXiv:1110.6875, October 31, 2011. http://arxiv.org/abs/1110.6875.

Mass = Epp quasilocal energy

E_E\equiv\frac{1}{8\pi G_N}\int_{\Omega}d^2x\sqrt{|\sigma|}\left(\sqrt{k^2-l^2}-\sqrt{\bar{k}^2-\bar{l}^2}\right)
EE≡18πGN∫Ωd2x∣σ∣(k2−l2−k¯2−l¯2)E_E\equiv\frac{1}{8\pi G_N}\int_{\Omega}d^2x\sqrt{|\sigma|}\left(\sqrt{k^2-l^2}-\sqrt{\bar{k}^2-\bar{l}^2}\right)
l\equiv\sigma^{\mu\nu}l_{\mu\nu}
l≡σμνlμνl\equiv\sigma^{\mu\nu}l_{\mu\nu}
k\equiv\sigma^{\mu\nu}k_{\mu\nu}
k≡σμνkμνk\equiv\sigma^{\mu\nu}k_{\mu\nu}
  • In 1+1 simplicial geometry, extrinsic curvature at a vertex is proportional to the number of connected triangles

 

  • In 2+1 simplicial geometry, extrinsic curvature at an edge is proportional to the number of connected tetrahedra

 

  • In 3+1 simplicial geometry, extrinsic curvature at a face is proportional to the number of connected pentachorons (4-simplices)

Non-Euclidean Distance

  • Calculate single-source shortest path between the two masses using Bellman-Ford algorithm in O(VE)
  • Modify allowed moves to not permit too many successive moves which increase or decrease distance between masses (hold relatively fixed)

 

Hausdorff Distance(?)

  • Calculate Voronoi diagram of Delaunay triangulation
  • Find minimal Hausdorff distance in diagram for sets in O((m+n)^6 log(mn)) (Huttenlocher, Kedem, and Kleinberg)

A Trick from GR

ds^{2} = e^{2\lambda}dt^{2} - e^{2\left(\nu-\lambda\right)}\left(dr^{2}+dz^{2}\right) - r^{2}e^{-2\lambda}d\phi^{2}
ds2=e2λdt2−e2(ν−λ)(dr2+dz2)−r2e−2λdϕ2 ds^{2} = e^{2\lambda}dt^{2} - e^{2\left(\nu-\lambda\right)}\left(dr^{2}+dz^{2}\right) - r^{2}e^{-2\lambda}d\phi^{2}

The static axisymmetric Weyl metric:

With two-body Chazy-Curzon (circa 1924) solutions of the Einstein field equations:

\lambda(r,z)=-\frac{\mu_1}{r_1}-\frac{\mu_2}{r_2}
λ(r,z)=−μ1r1−μ2r2\lambda(r,z)=-\frac{\mu_1}{r_1}-\frac{\mu_2}{r_2}
\nu(r,z)=\frac{1}{2}\frac{\mu_{1}^{2}r^2}{r_{1}^{4}}-\frac{1}{2}\frac{\mu_{2}^{2}r^2}{r_{2}^{4}}+\frac{2\mu_1\mu_2}{(z-z_2)^2}\left[\frac{r^2+(z-z_1)(z-z_2)}{r_{1}r_{2}}-1\right]
ν(r,z)=12μ12r2r14−12μ22r2r24+2μ1μ2(z−z2)2[r2+(z−z1)(z−z2)r1r2−1]\nu(r,z)=\frac{1}{2}\frac{\mu_{1}^{2}r^2}{r_{1}^{4}}-\frac{1}{2}\frac{\mu_{2}^{2}r^2}{r_{2}^{4}}+\frac{2\mu_1\mu_2}{(z-z_2)^2}\left[\frac{r^2+(z-z_1)(z-z_2)}{r_{1}r_{2}}-1\right]
r_1=\sqrt{r^2+(z-z_1)^2}
r1=r2+(z−z1)2r_1=\sqrt{r^2+(z-z_1)^2}

Leads to a strut:

With a stress:

That can be integrated to get the Newtonian force!

\nu(0,z)=\frac{4\mu_{1}\mu_{2}}{z_{1}^2-z_{2}^2}
ν(0,z)=4μ1μ2z12−z22\nu(0,z)=\frac{4\mu_{1}\mu_{2}}{z_{1}^2-z_{2}^2}
T_{zz}=\frac{1}{8\pi G_{N}}\left(1-e^{-\nu(r,z)}\right)2\pi\delta
Tzz=18πGN(1−e−ν(r,z))2πδT_{zz}=\frac{1}{8\pi G_{N}}\left(1-e^{-\nu(r,z)}\right)2\pi\delta
F=\int T_{zz}dA=\frac{1}{4G_{N}}\left(1-e^{-\nu(r,z)}\right)=G_{N}\frac{m_1m_2}{z_1^2-z_2^2}\:\text{for}\:\mu_i=G_Nm_i
F=∫TzzdA=14GN(1−e−ν(r,z))=GNm1m2z12−z22forμi=GNmiF=\int T_{zz}dA=\frac{1}{4G_{N}}\left(1-e^{-\nu(r,z)}\right)=G_{N}\frac{m_1m_2}{z_1^2-z_2^2}\:\text{for}\:\mu_i=G_Nm_i

A Trick from GR

ds^{2} = e^{2\lambda}dt^{2} - e^{2\left(\nu-\lambda\right)}\left(dr^{2}+dz^{2}\right) - r^{2}e^{-2\lambda}d\phi^{2}
ds2=e2λdt2−e2(ν−λ)(dr2+dz2)−r2e−2λdϕ2 ds^{2} = e^{2\lambda}dt^{2} - e^{2\left(\nu-\lambda\right)}\left(dr^{2}+dz^{2}\right) - r^{2}e^{-2\lambda}d\phi^{2}
g_{\mu\nu}=\left(\begin{array}{cccc} e^{2\lambda} & 0 & 0 & 0\\ 0 & -e^{2\left(\nu-\lambda\right)} & 0 & 0\\ 0 & 0 & -e^{2\left(\nu-\lambda\right)} & 0\\ 0 & 0 & 0 & -\frac{r^{2}}{e^{2\lambda}} \end{array}\right)
gμν=(e2λ0000−e2(ν−λ)0000−e2(ν−λ)0000−r2e2λ)g_{\mu\nu}=\left(\begin{array}{cccc} e^{2\lambda} & 0 & 0 & 0\\ 0 & -e^{2\left(\nu-\lambda\right)} & 0 & 0\\ 0 & 0 & -e^{2\left(\nu-\lambda\right)} & 0\\ 0 & 0 & 0 & -\frac{r^{2}}{e^{2\lambda}} \end{array}\right)
\Gamma_{\mu\nu}^{\lambda}=\frac{1}{2}g^{\lambda\sigma}\left(\partial_{\mu}g_{\nu\sigma}+\partial_{\nu}g_{\sigma\mu}-\partial_{\sigma}g_{\mu\nu}\right)
Γμνλ=12gλσ(∂μgνσ+∂νgσμ−∂σgμν)\Gamma_{\mu\nu}^{\lambda}=\frac{1}{2}g^{\lambda\sigma}\left(\partial_{\mu}g_{\nu\sigma}+\partial_{\nu}g_{\sigma\mu}-\partial_{\sigma}g_{\mu\nu}\right)
R_{\sigma\mu\nu}^{\rho}=\partial_{\mu}\Gamma_{\nu\sigma}^{\rho}-\partial_{\nu}\Gamma_{\mu\sigma}^{\rho}+\Gamma_{\mu\lambda}^{\rho}\Gamma_{\nu\sigma}^{\lambda}-\Gamma_{\nu\lambda}^{\rho}\Gamma_{\mu\sigma}^{\lambda}
Rσμνρ=∂μΓνσρ−∂νΓμσρ+ΓμλρΓνσλ−ΓνλρΓμσλR_{\sigma\mu\nu}^{\rho}=\partial_{\mu}\Gamma_{\nu\sigma}^{\rho}-\partial_{\nu}\Gamma_{\mu\sigma}^{\rho}+\Gamma_{\mu\lambda}^{\rho}\Gamma_{\nu\sigma}^{\lambda}-\Gamma_{\nu\lambda}^{\rho}\Gamma_{\mu\sigma}^{\lambda}
R_{\mu\nu}=R^{\rho}_{\mu\rho\nu}
Rμν=RμρνρR_{\mu\nu}=R^{\rho}_{\mu\rho\nu}
R=R^{\mu}_{\mu}
R=RμμR=R^{\mu}_{\mu}
R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}
Rμν−12Rgμν=8πGNTμνR_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}

Metric

Affine connection

Riemann tensor

Ricci tensor & Ricci scalar

Einstein field equations

Made with Slides.com