Quantum Gravity Using (Hidden) Markov Models

Adam Getchell

University of California, Davis

Department of Physics

Why?

"Nevertheless, due to the interatomic movements of electrons, atoms would have to radiate not only electromagnetic but also gravitational energy, if only in tiny amounts. As this is hardly true in nature, it appears that quantum theory would have to modify not only Maxwellian electrodynamics, but also the new theory of gravitation."

 

— A. Einstein, Approximative Integrations of the Field Equations of Gravitation, 1916

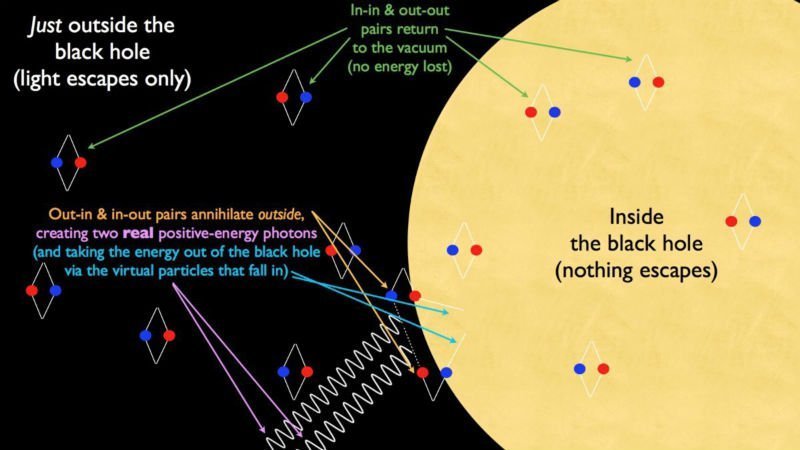
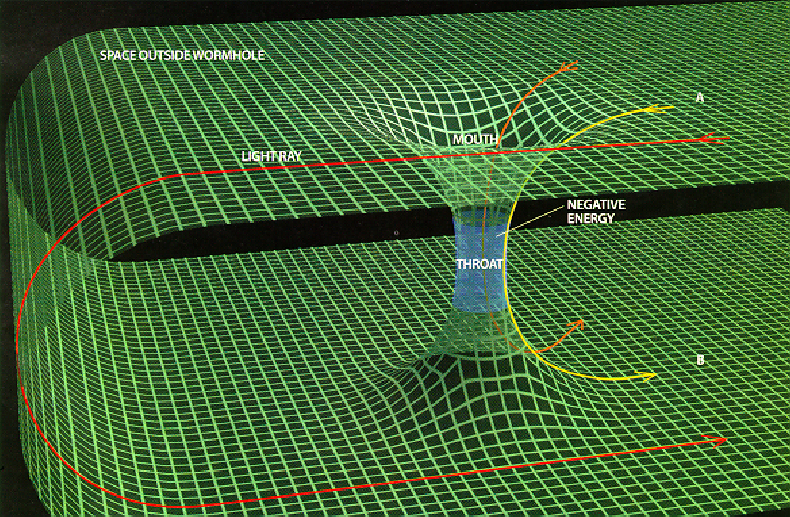
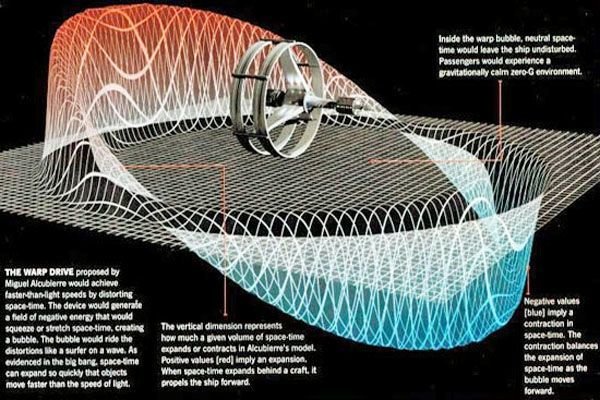
Synopsis

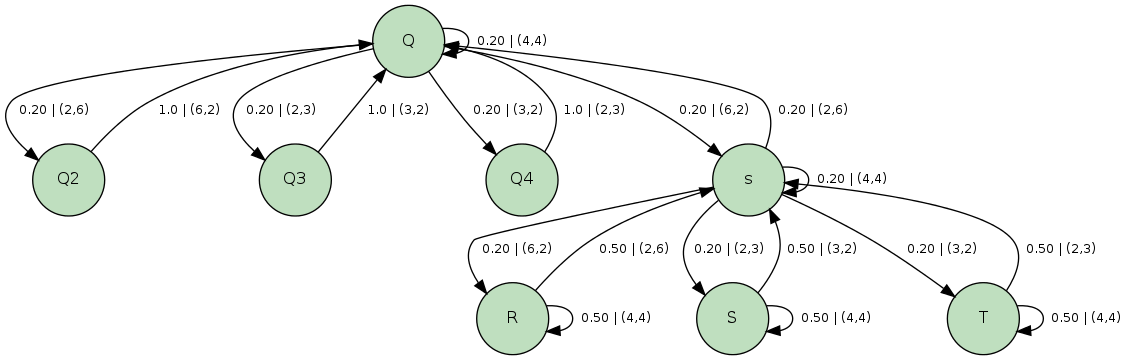
Set of States

256 timeslices, 222,132 vertices,  2,873,253 faces, 1,436,257 simplices

Output Alphabet

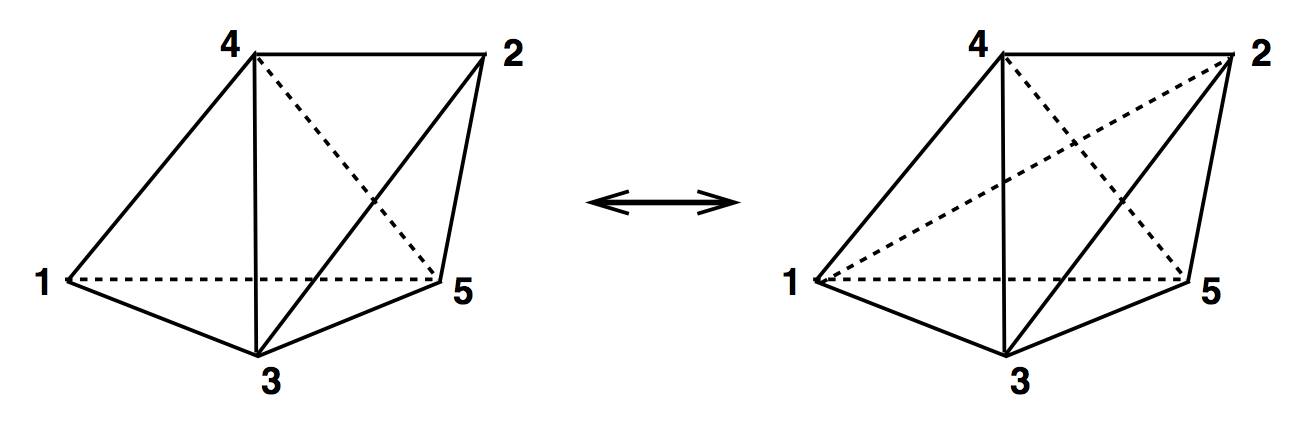
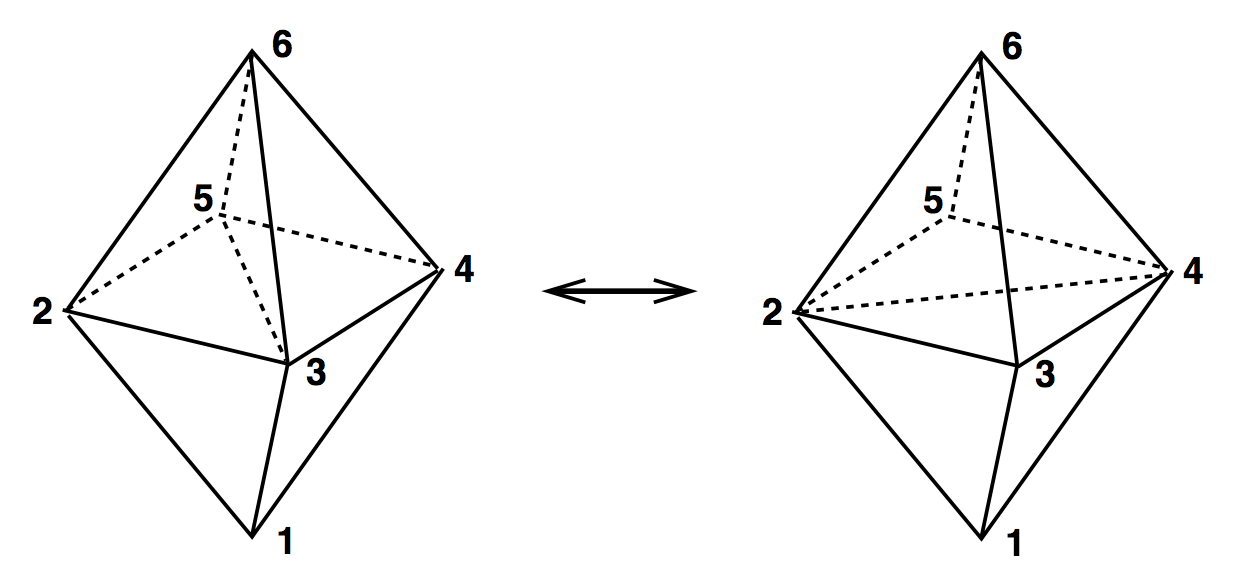
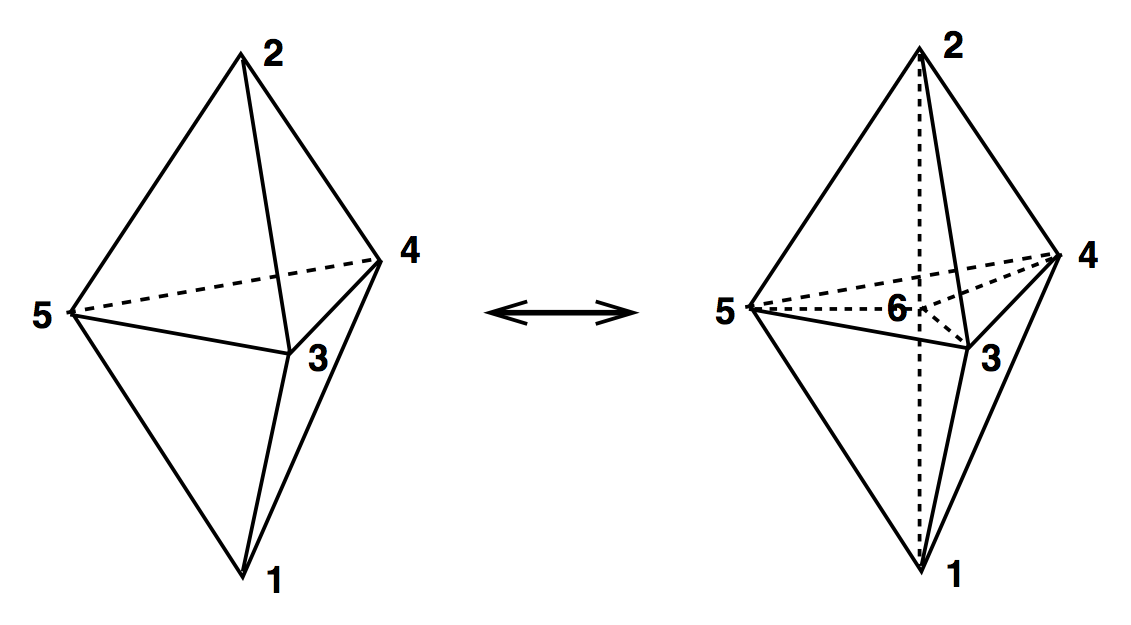
(2,3) & (3,2)

(4,4)

(2,6) & (6,2)

Simplices involved

Move name

(3,1) & (2,2)

2 (1,3) & 2 (3,1)

(1,3) & (3,1)

Transition Probabilities

  1. Pick an ergodic (Pachner) move
  2. Make that move with a probability of a=a1a2, where:
a_{1}=\frac{move[i]}{\sum\limits_{i}move[i]}
a1=move[i]∑imove[i]a_{1}=\frac{move[i]}{\sum\limits_{i}move[i]}
a_{2}=e^{\Delta I}
a2=eΔIa_{2}=e^{\Delta I}
I_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)
IR=18πGN(∑hingesAhδh−Λ∑simplicesVs)I_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)

Output Probabilities

\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-I_{R}(T)}
⟨B∣T∣A⟩=∑triangulations1C(T)e−IR(T)\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-I_{R}(T)}

Wick rotation

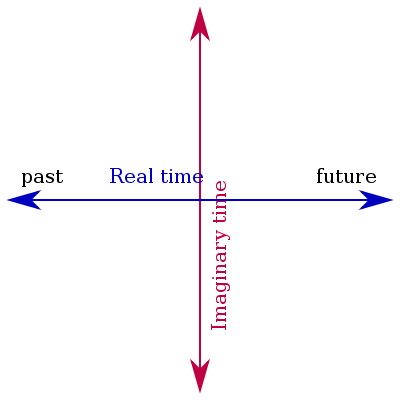
Background

R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}
Rμν−12Rgμν=8πGNTμνR_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}

Parallel Transport

ds^{2} = e^{2\lambda}dt^{2} - e^{2\left(\nu-\lambda\right)}\left(dr^{2}+dz^{2}\right) - r^{2}e^{-2\lambda}d\phi^{2}
ds2=e2λdt2−e2(ν−λ)(dr2+dz2)−r2e−2λdϕ2 ds^{2} = e^{2\lambda}dt^{2} - e^{2\left(\nu-\lambda\right)}\left(dr^{2}+dz^{2}\right) - r^{2}e^{-2\lambda}d\phi^{2}
g_{\mu\nu}=\left(\begin{array}{cccc} e^{2\lambda} & 0 & 0 & 0\\ 0 & -e^{2\left(\nu-\lambda\right)} & 0 & 0\\ 0 & 0 & -e^{2\left(\nu-\lambda\right)} & 0\\ 0 & 0 & 0 & -\frac{r^{2}}{e^{2\lambda}} \end{array}\right)
gμν=(e2λ0000−e2(ν−λ)0000−e2(ν−λ)0000−r2e2λ)g_{\mu\nu}=\left(\begin{array}{cccc} e^{2\lambda} & 0 & 0 & 0\\ 0 & -e^{2\left(\nu-\lambda\right)} & 0 & 0\\ 0 & 0 & -e^{2\left(\nu-\lambda\right)} & 0\\ 0 & 0 & 0 & -\frac{r^{2}}{e^{2\lambda}} \end{array}\right)
\Gamma_{\mu\nu}^{\lambda}=\frac{1}{2}g^{\lambda\sigma}\left(\partial_{\mu}g_{\nu\sigma}+\partial_{\nu}g_{\sigma\mu}-\partial_{\sigma}g_{\mu\nu}\right)
Γμνλ=12gλσ(∂μgνσ+∂νgσμ−∂σgμν)\Gamma_{\mu\nu}^{\lambda}=\frac{1}{2}g^{\lambda\sigma}\left(\partial_{\mu}g_{\nu\sigma}+\partial_{\nu}g_{\sigma\mu}-\partial_{\sigma}g_{\mu\nu}\right)
R_{\sigma\mu\nu}^{\rho}=\partial_{\mu}\Gamma_{\nu\sigma}^{\rho}-\partial_{\nu}\Gamma_{\mu\sigma}^{\rho}+\Gamma_{\mu\lambda}^{\rho}\Gamma_{\nu\sigma}^{\lambda}-\Gamma_{\nu\lambda}^{\rho}\Gamma_{\mu\sigma}^{\lambda}
Rσμνρ=∂μΓνσρ−∂νΓμσρ+ΓμλρΓνσλ−ΓνλρΓμσλR_{\sigma\mu\nu}^{\rho}=\partial_{\mu}\Gamma_{\nu\sigma}^{\rho}-\partial_{\nu}\Gamma_{\mu\sigma}^{\rho}+\Gamma_{\mu\lambda}^{\rho}\Gamma_{\nu\sigma}^{\lambda}-\Gamma_{\nu\lambda}^{\rho}\Gamma_{\mu\sigma}^{\lambda}
R_{\mu\nu}=R^{\rho}_{\mu\rho\nu}
Rμν=RμρνρR_{\mu\nu}=R^{\rho}_{\mu\rho\nu}
R=R^{\mu}_{\mu}
R=RμμR=R^{\mu}_{\mu}

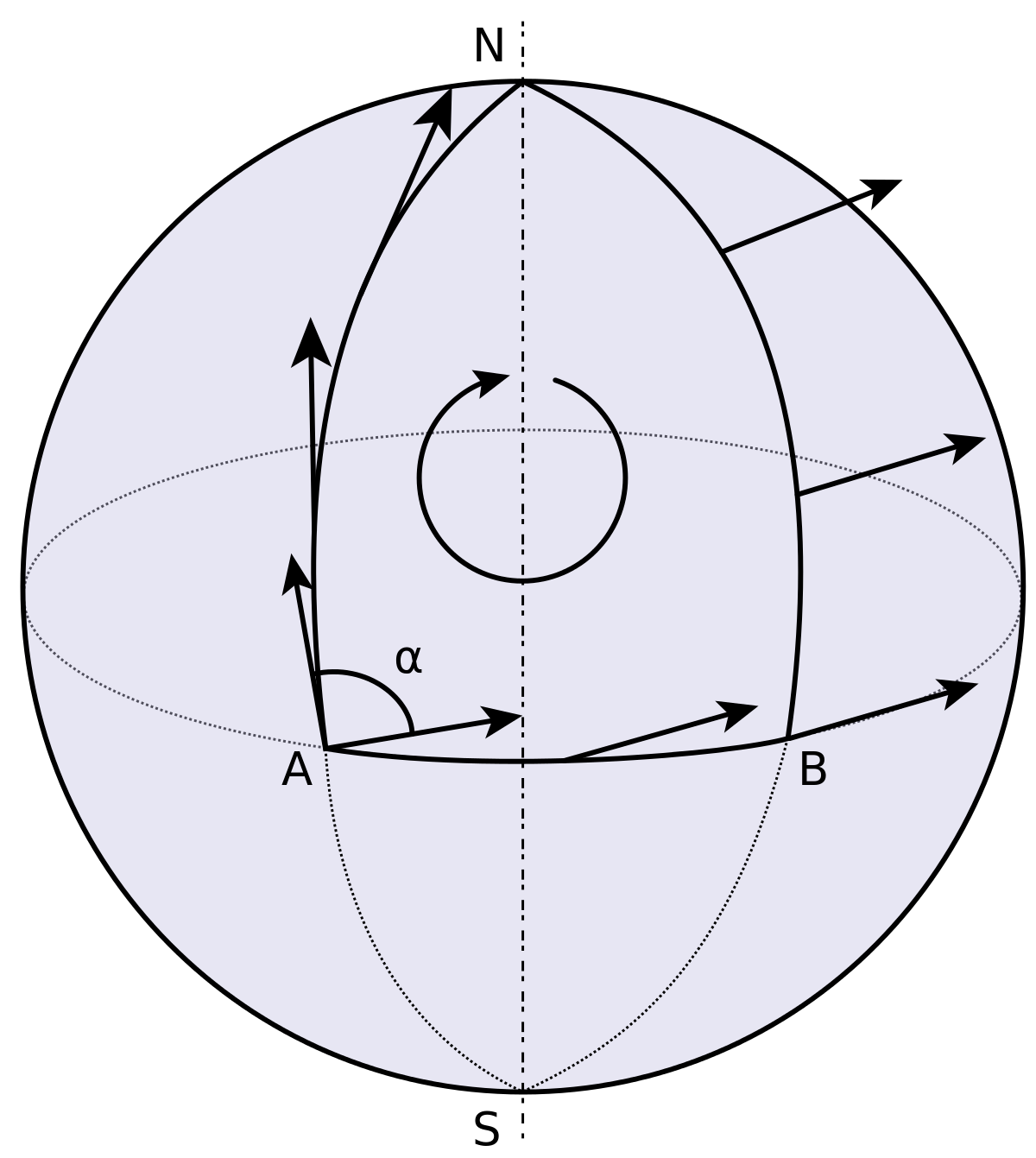
Metric

Affine connection

Riemann tensor

Ricci tensor & Ricci scalar

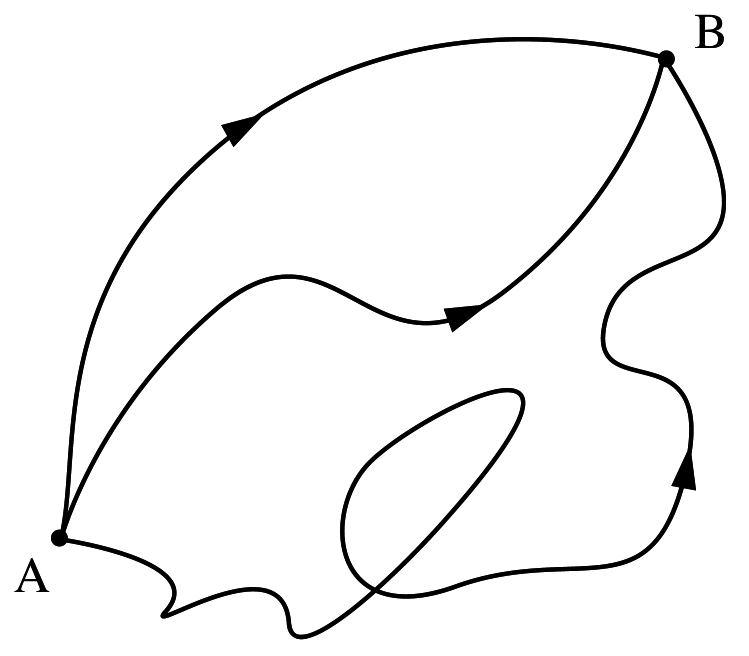
Path Integral

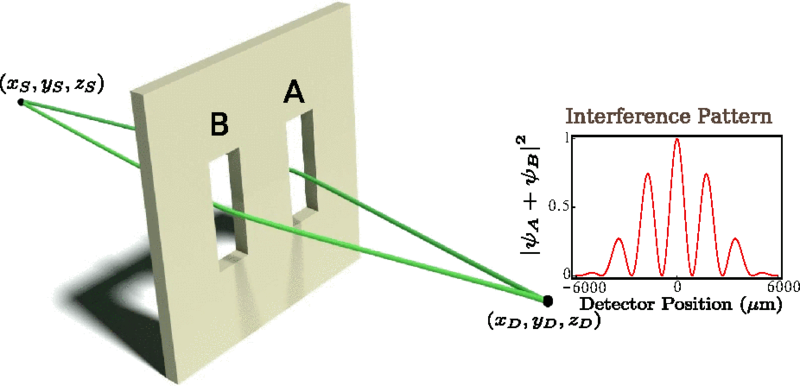
Path Integral

\langle B|T|A\rangle=\int\mathcal{D}[g]e^{iI_{EH}}
⟨B∣T∣A⟩=∫D[g]eiIEH\langle B|T|A\rangle=\int\mathcal{D}[g]e^{iI_{EH}}
I_{EH}=\frac{1}{16\pi G_{N}}\int d^{4}x\sqrt{-g}(R-2\Lambda)
IEH=116πGN∫d4x−g(R−2Λ) I_{EH}=\frac{1}{16\pi G_{N}}\int d^{4}x\sqrt{-g}(R-2\Lambda)

Equations of Motion

\partial S = 0 \rightarrow R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}
∂S=0→Rμν−12Rgμν=8πGNTμν\partial S = 0 \rightarrow R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}

Ricci scalar

Cosmological constant

Ricci tensor

Ricci scalar

Stress-Energy tensor

Transition probability amplitude

Simplicial Manifolds

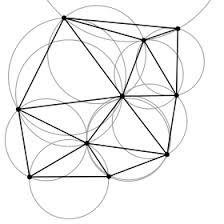
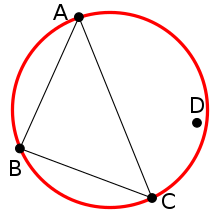
Delaunay Triangulation

Not a Delaunay Triangulation

DT Path Integral

\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{iI_{R}(T)}
⟨B∣T∣A⟩=∑triangulations1C(T)eiIR(T)\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{iI_{R}(T)}
I_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)
IR=18πGN(∑hingesAhδh−Λ∑simplicesVs)I_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)

Inequivalent Triangulations

Regge Action

Partition Function

Transition probability amplitude

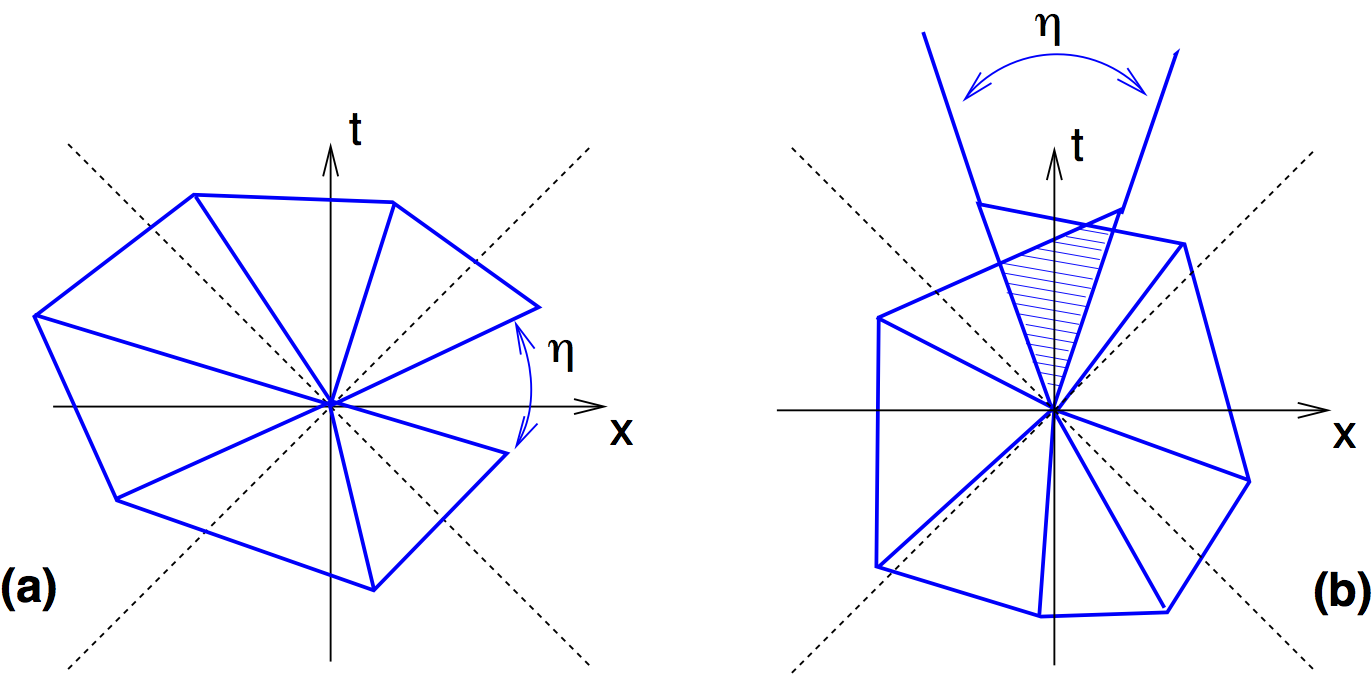
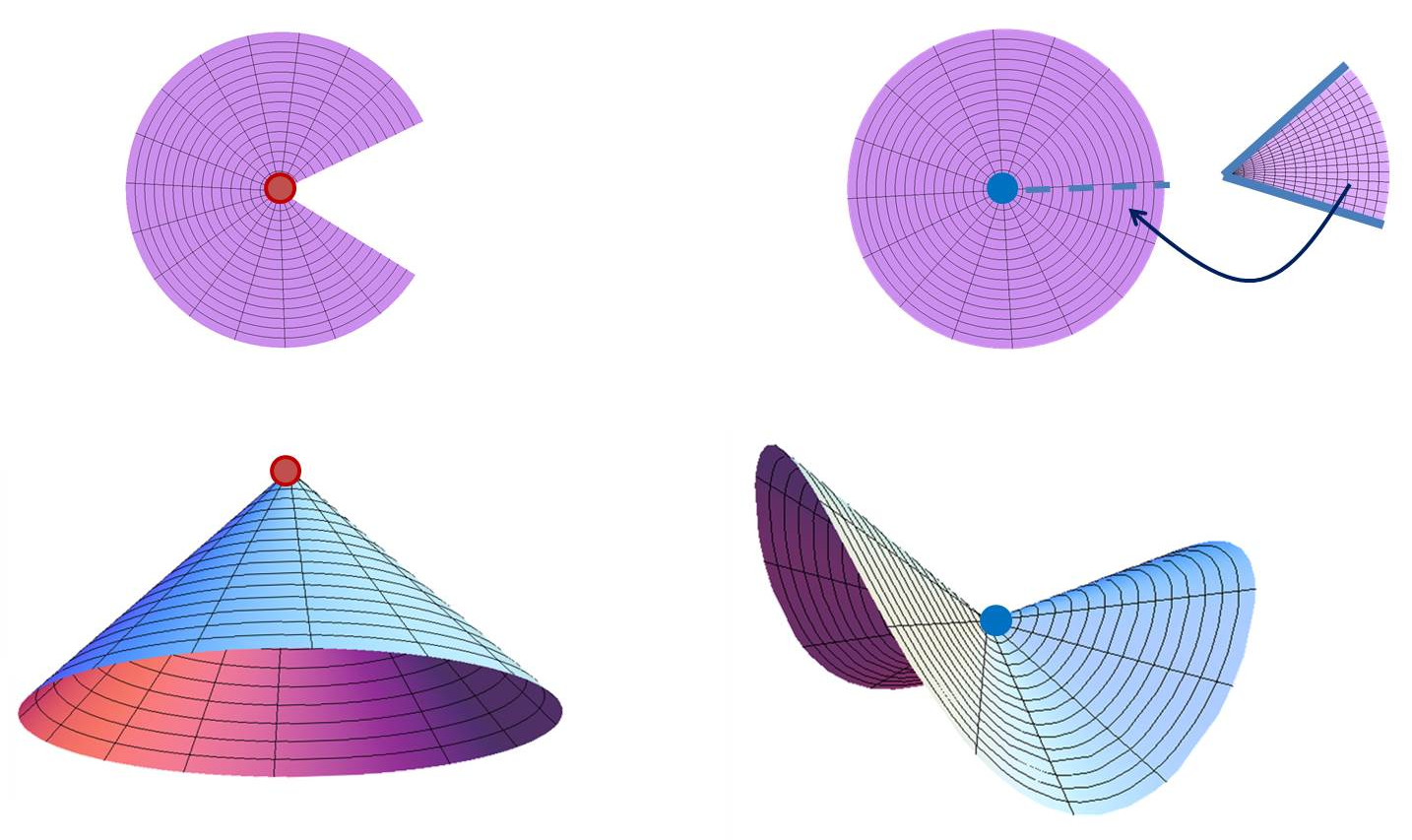
Foliation

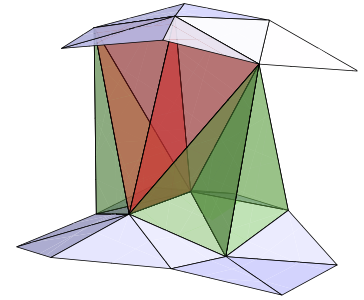
Mass = Epp quasilocal energy

E_E\equiv\frac{1}{8\pi G_N}\int_{\Omega}d^2x\sqrt{|\sigma|}\left(\sqrt{k^2-l^2}-\sqrt{\bar{k}^2-\bar{l}^2}\right)
EE≡18πGN∫Ωd2x∣σ∣(k2−l2−kˉ2−lˉ2)E_E\equiv\frac{1}{8\pi G_N}\int_{\Omega}d^2x\sqrt{|\sigma|}\left(\sqrt{k^2-l^2}-\sqrt{\bar{k}^2-\bar{l}^2}\right)
l\equiv\sigma^{\mu\nu}l_{\mu\nu}
l≡σμνlμνl\equiv\sigma^{\mu\nu}l_{\mu\nu}
k\equiv\sigma^{\mu\nu}k_{\mu\nu}
k≡σμνkμνk\equiv\sigma^{\mu\nu}k_{\mu\nu}
  • In 1+1 simplicial geometry, extrinsic curvature at a vertex is proportional to the number of connected triangles

 

  • In 2+1 simplicial geometry, extrinsic curvature at an edge is proportional to the number of connected tetrahedra

 

  • In 3+1 simplicial geometry, extrinsic curvature at a face is proportional to the number of connected pentachorons (4-simplices)

CDT Action

\begin{array}{l} S^{(3)} &=& 2\pi k\sqrt{\alpha}N_1^{TL} \\ &+& N_3^{(3,1)}\left[-3k\text{arcsinh}\left(\frac{1}{\sqrt{3} \sqrt{4\alpha +1}}\right)-3k\sqrt{\alpha}\text{arccos}\left(\frac{2\alpha+1} {4\alpha+1}\right)-\frac{\lambda}{12}\sqrt{3\alpha+1}\right] \\ &+& N_3^{(2,2)}\left[2k\text{arcsinh}\left(\frac{2\sqrt{2}\sqrt{2\alpha+1}} {4\alpha +1}\right)-4k\sqrt{\alpha}\text{arccos}\left(\frac{-1}{4\alpha+1} \right)-\frac{\lambda}{12}\sqrt{4\alpha +2}\right] \end{array}
S(3)=2πkαN1TL+N3(3,1)[−3karcsinh(134α+1)−3kαarccos(2α+14α+1)−λ123α+1]+N3(2,2)[2karcsinh(222α+14α+1)−4kαarccos(−14α+1)−λ124α+2]\begin{array}{l} S^{(3)} &=& 2\pi k\sqrt{\alpha}N_1^{TL} \\ &+& N_3^{(3,1)}\left[-3k\text{arcsinh}\left(\frac{1}{\sqrt{3} \sqrt{4\alpha +1}}\right)-3k\sqrt{\alpha}\text{arccos}\left(\frac{2\alpha+1} {4\alpha+1}\right)-\frac{\lambda}{12}\sqrt{3\alpha+1}\right] \\ &+& N_3^{(2,2)}\left[2k\text{arcsinh}\left(\frac{2\sqrt{2}\sqrt{2\alpha+1}} {4\alpha +1}\right)-4k\sqrt{\alpha}\text{arccos}\left(\frac{-1}{4\alpha+1} \right)-\frac{\lambda}{12}\sqrt{4\alpha +2}\right] \end{array}

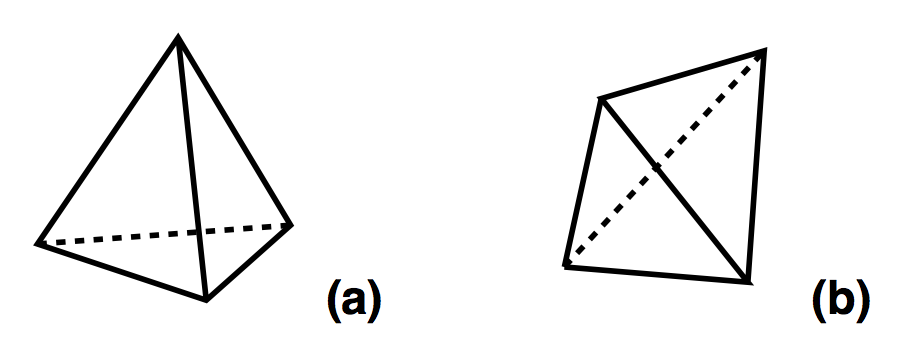
Metropolis-Hastings

  1. Pick an ergodic (Pachner) move
  2. Make that move with a probability of a=a1a2, where:
a_{1}=\frac{move[i]}{\sum\limits_{i}move[i]}
a1=move[i]∑imove[i]a_{1}=\frac{move[i]}{\sum\limits_{i}move[i]}
a_{2}=e^{\Delta I}
a2=eΔIa_{2}=e^{\Delta I}
I_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)
IR=18πGN(∑hingesAhδh−Λ∑simplicesVs)I_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)

Transition Amplitudes

\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-I_{R}(T)}
⟨B∣T∣A⟩=∑triangulations1C(T)e−IR(T)\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-I_{R}(T)}

Wick rotation

Made with Slides.com