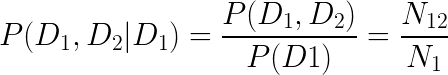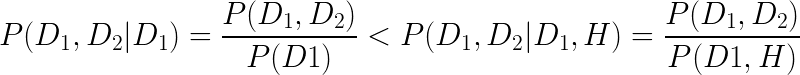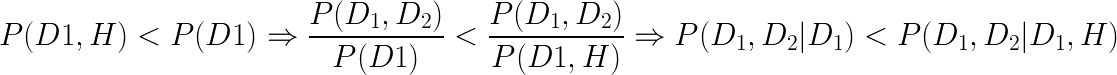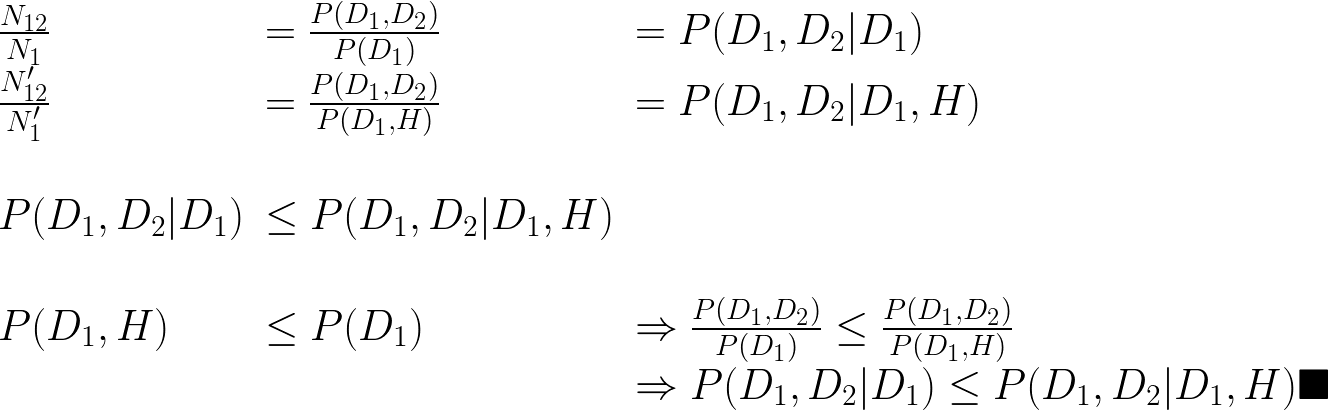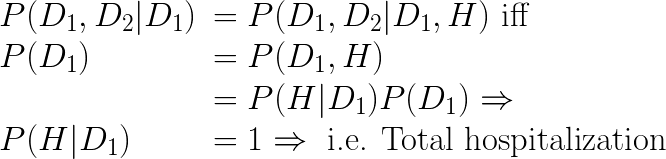Outline
- Bias & Selection bias
- Consequences of selection bias
- Causal representation of different biases
- eQTL
- PCA adjustment in eQTL
- Bias for PCA adjustment
Detecting, Quantifying and Correcting Selection Bias due to PCA adjustment in eQTL discovery
Alex Couto Alves
Bias vs Noise
-
Systematic Error (Bias): Systematic difference between population parameter and the estimated statistics.
-
Random Error (Noise): Random difference between population parameter and the estimated statistics.

Nomenclature
-
Selection Bias
-
Collider bias
-
Berkson bias


Does gallstones cause diabetes?

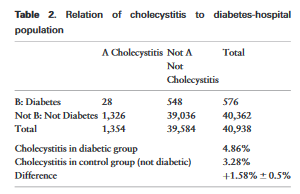
Ratio of multiple diagnosis to single diagnosis in the hospital is always greater than in the general population


"
Selection bias
D1
H
D2
A causal model
E
G

Suppression & Selection Bias

PCA of gene expression

(Matthias Scholz, Ph.D. thesis)
PC1 = Weight11 * Expression Gene 1 + Weight12 * Expression Gene 2 + …
PC2 = Weight21 * Expression Gene 1 + Weight22 * Expression Gene 2 + …
Expression quantitative trait loci mapping

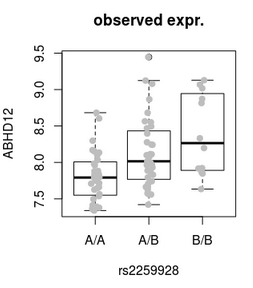
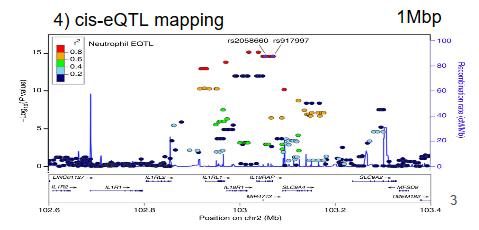

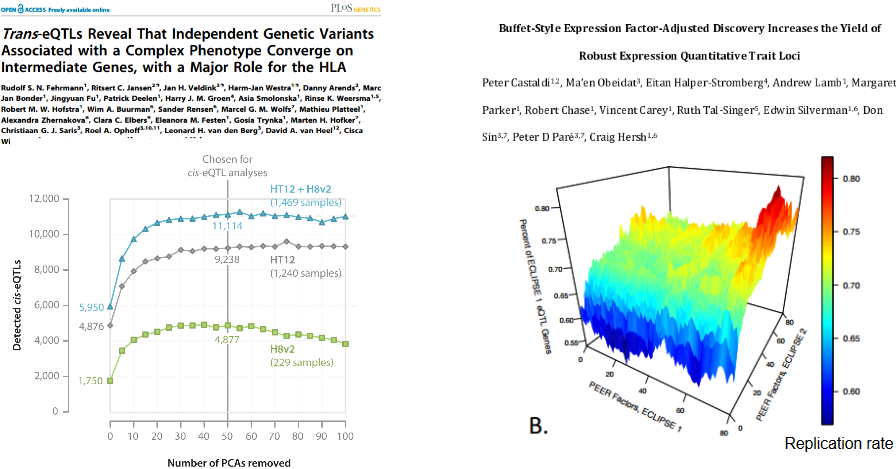
Adjustment for expression PCs increase the yield of cis-eQTLs
H
SNP
SNPt
Gt
G
S
B
PCA
?
S


Causation vs bias and confounding in genetic association studies

Detection of selection bias
- Increasing PCs increases numbers of replicable eQTLs
- PCs are functionally defined from expression
- eQTL associations adjusting for PC recapitulate selection bias causal structure
- Numerical simulations illustrate two types of selection bias
- Empirical assessments suggests effect sizes of some eQTLs are biased
Functional definition of Expression PC
Selection Bias & Endogeneity Bias


PCA selection bias
D1
H
D2
A causal model
E2
E1
G1
PC1
G2
SNP2
SNP1
Gg
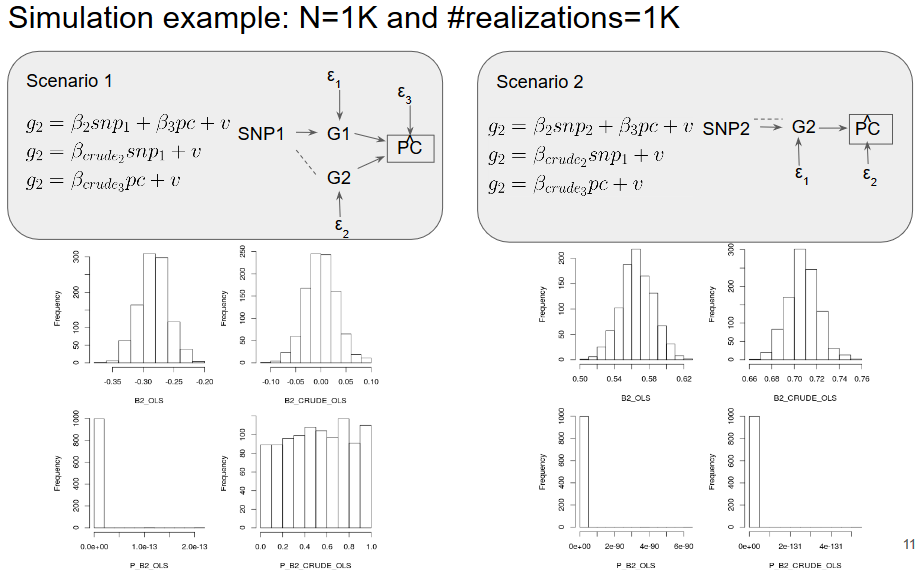
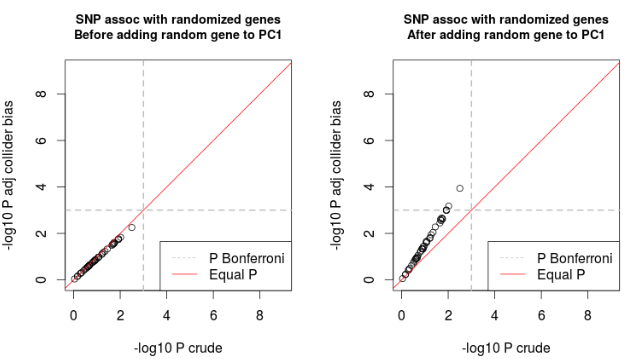
Simulation PCA Selection Bias
Empirical assessment


Empirical assessment
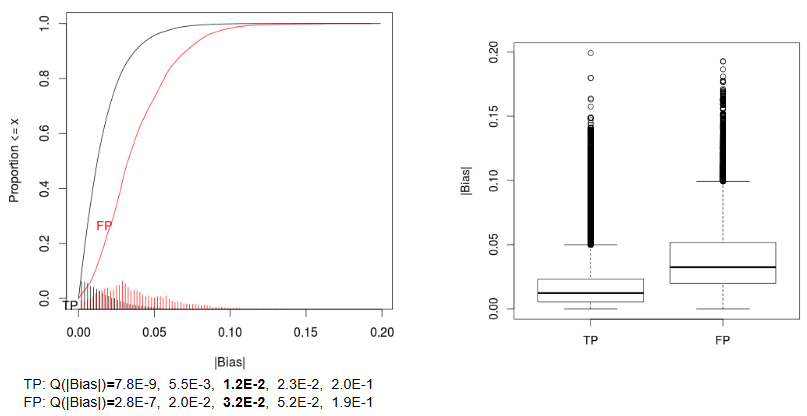


Quantification of Selection Bias
- GWAS assumptions excludes confounder bias
- Mathematical analysis of the regression coefficients estimates reveals bias factor is independent of the genetic effect
- Construction of a null model of no genetic effect shows the possibility of FP induced by bias alone
- Construction of a test statistic corrected for the biases on effect size and SE estimates
- Principled detection of putative true & false positives
- Quantification of the FP and FN due to selection bias
selection bias in the regression coefficients estimates





A null model of no genetic effect
(Betas induced by Selection Bias)


A test for regression coefficients adjusting for selection bias and suppression


Principled definition of TP/FP

Significant associations with null genetic effect
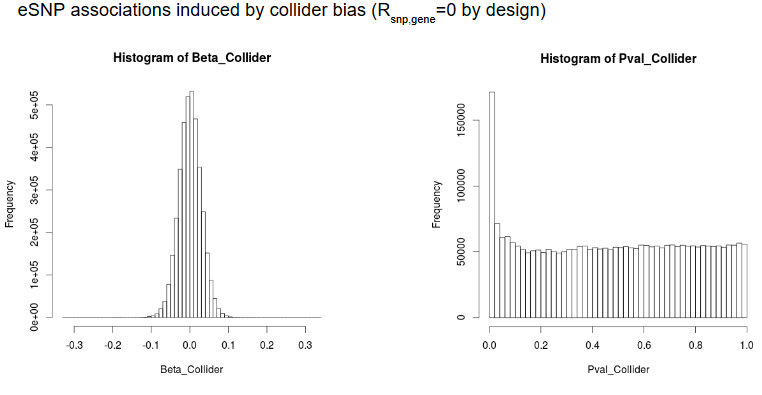

Bias-induced FP/FN
Fat expression
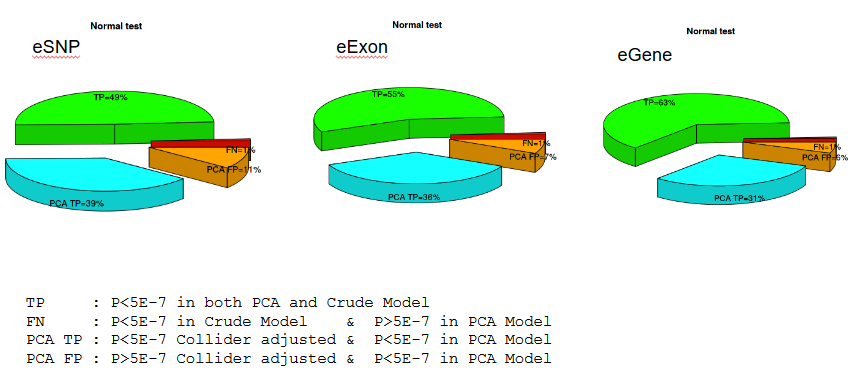

Bias-induced FP/FN
LCL expression
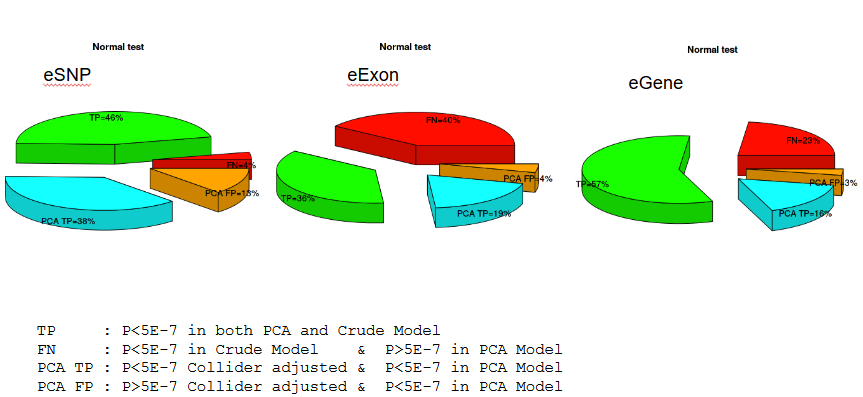




Correction of Selection Bias
- Randomization of real data assesses bias correction validity
- P-values corrected for bias are validated against the null of no genetic effect with and without PC-induced selection bias
- Betas adjusted for bias are validated against the null of no genetic effect
Design of the experiment

Correction of selection bias
P-values
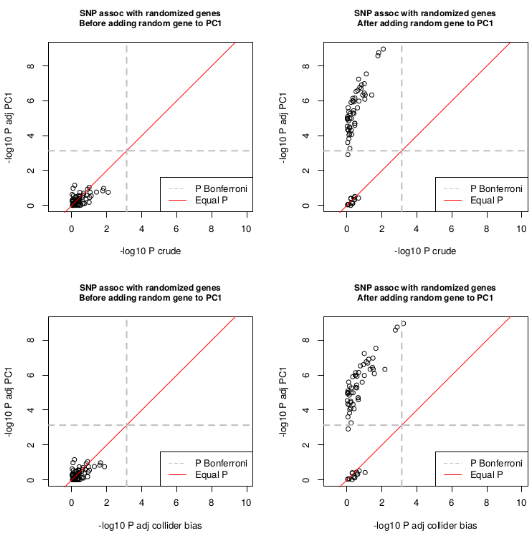
Confounding in genetic associations
Crude and PC adjusted models
Confounding
LCL
| 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | |||||||||
| 3 |
Genotypes
| 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | |||||||||
Expression
SNP
? B1
G
B2
C
?
1M
317K
610K
Expression batch effects

Confounding analysis
Crude model

Confounding analysis
PC adjusted model

Artificial confounding
Emulating missing data impution to ref
SNP
B1
G
B2
C
Genotypes
Expression
Artificial confounding
Crude model

Artificial confounding
PC adjusted model

Conclusion
- Models with adjustment for expression PCs explain variation on Y using variation on Y
- This causes endogeneity biases, including selection bias and suppression.
- Correction of selection bias in genetic studies is possible because of knowledge of the theoretical causal model and the assumption of no confounding
- It is possible to mitigate confounding in properly designed genetic association studies.
- Violations to the assumption of no confounding, can severely affect both PC-adjusted and crude model estimates, but less so in PC-adjusted models

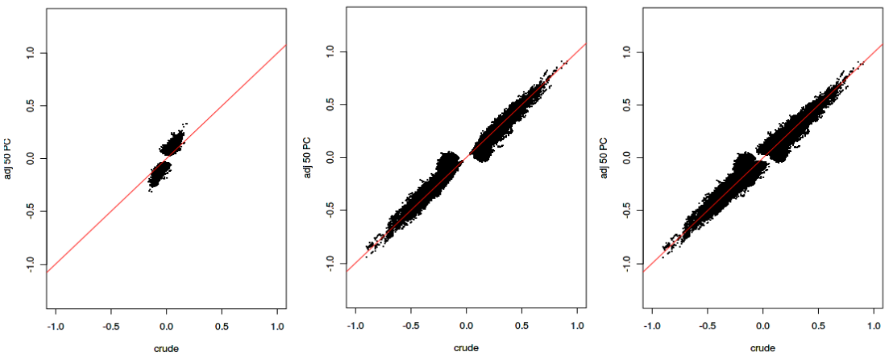
Correction of selection bias
Beta values
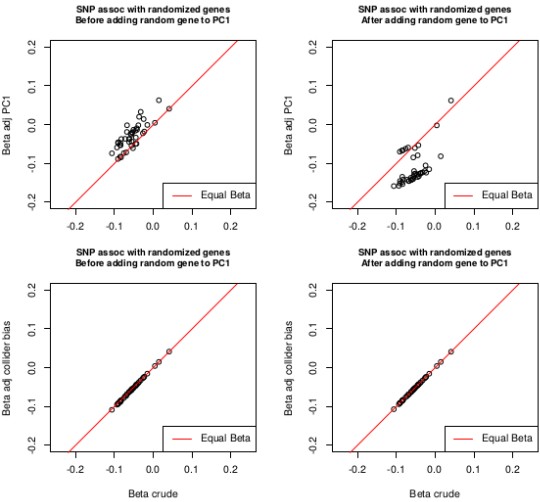
Correction of selection bias
P-values
Empirical assessment

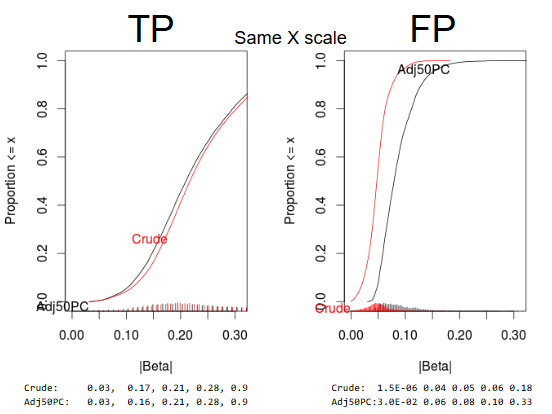
Empirical assessment
FP
TP
All

Basic causal structures
X
Y
- C
- X
- Y
- C
Confounder
- X
- Y
- C
- X
- Y
- C
Collider
X
Y
- M
- X
- Y
- M
Mediator
- X
- Y
- E
- X
- Y
- E
Exogenous variable


Does the causes of gallstones cause diabetes?
- E
- D1
- D2
- H
- G
- E
- D1
- D2
- H
- G
- D1
- D2
- H
Joseph Berkson (1899 – 1982)
- 1922 M.A. Physics, Columbia
- 1927 M.D., Johns Hopkins
- 1928 Dr.Sc., Johns Hopkins
- 1933 Head of Biometry and Medical Statistics ,Mayo Clinic
- 1946 Legion of Honour, US War Dept
From Biometrics Vol. 39, No. 4 (Dec., 1983), pp. 1107-1111
D1
H
D2
D1
H
D2
A B


Identities
Selection bias
- Only total hospitalization avoids Berkson bias: