Ako sa dostať do vesmíru

Jakub Havelka    Adam Dej

Časť 1: Orbita

Čo je to orbita?

  • Každá dráha zakrivená graviáciou
  • Newton dokázal že sú to kuželosečky

Ako opísať orbitu?

  • Výstrednosť dráhy (Eccentricity)
  • Veľká polos (Semimajor axis)
  • Uhol sklonu (Inclination)
  • Dĺžka výstupného uzla (Longitude of the ascending node)
  • Argument periapsy (Argument of periapsis)
  • Stredná anomália (Mean anomaly at epoch)

Orbitálna rýchlosť v danom bode

Pre skoro kruhové orbity

v_0 \approx \frac{2 \pi a}{T}
v0≈2πaTv_0 \approx \frac{2 \pi a}{T}

Pre excentrické orbity

v = \sqrt{GM_{zem}\left( \frac{2}{r} - \frac{1}{a}\right)}
v=GMzem(2r−1a)v = \sqrt{GM_{zem}\left( \frac{2}{r} - \frac{1}{a}\right)}

Geosynchrónna orbita

  • Pozorovateľ na zemi vidí satelit vo fixnom bode na oblohe
v_{gs} = 3.1 \frac{km}{s}
vgs=3.1kmsv_{gs} = 3.1 \frac{km}{s}

Vzdialenosti stredov: ~42 000 km

Časť 2: Ako fungujú rakety?

Raketové motory

  • Reakčné motory - tretí Newtonov zákon
  • Čím rýchlejší výfuk tým lepšie
    • ISP - špecifický impulz
  • Tekuté palivo
  • Tuhé palivo
  • Hybridné
  • Termálne
  • Monopropellant

Delta-v

  • Motor pôsobí na raketu nejakou silou
a = \frac{F}{m}
a=Fma = \frac{F}{m}
  • Hmotnosť rakety klesá, míňame palivo
     
  • Zaujímavá informácia: zmena rýchlosti
    • Ktorú sme schopní dosiahnuť s palivom ktoré máme
\Delta v = \int_{t_0}^{t} \frac{F} {m_t} dt
Δv=∫t0tFmtdt\Delta v = \int_{t_0}^{t} \frac{F} {m_t} dt

Tsiolkovského rovnica

\Delta v = v_e ~ ln\frac{m_0}{m_1}
Δv=ve lnm0m1\Delta v = v_e ~ ln\frac{m_0}{m_1}
v_e = g_0 ~ I_{sp}
ve=g0 Ispv_e = g_0 ~ I_{sp}
\Delta v = v_e ln \frac{100}{100 - 80} \approx 1.61 v_e
Δv=veln100100−80≈1.61ve\Delta v = v_e ln \frac{100}{100 - 80} \approx 1.61 v_e
\Delta v = 3 \cdot v_e ln \frac{100}{100 - 80} \approx 4.83 v_e
Δv=3⋅veln100100−80≈4.83ve\Delta v = 3 \cdot v_e ln \frac{100}{100 - 80} \approx 4.83 v_e
\Delta v = v_e ln \frac{100}{100 - 11.2} \approx 2.19 v_e
Δv=veln100100−11.2≈2.19ve\Delta v = v_e ln \frac{100}{100 - 11.2} \approx 2.19 v_e

Staging

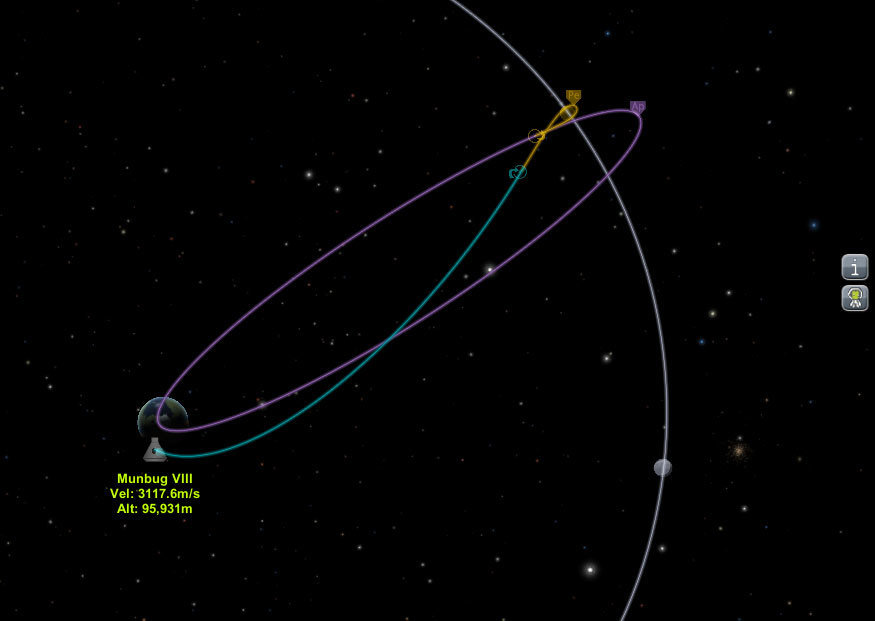
Časť 3: Ako meniť orbitu?

Menenie Ap / Pe

Z druheho Keplerovho zákona

r v ~ sin\gamma = \omega r ^2 = \mathrm{const}
rv sinγ=ωr2=constr v ~ sin\gamma = \omega r ^2 = \mathrm{const}

Teda pre periapsu a apoapsu:

r_p v_p = r_av_a
rpvp=ravar_p v_p = r_av_a

Menenie Ap / Pe

Kinetická a potenciálna energia

E_k = \frac{mv^2}{2}
Ek=mv22E_k = \frac{mv^2}{2}
E_p = - \frac{GM m}{r}
Ep=−GMmrE_p = - \frac{GM m}{r}

Zákon zachovania energie

\frac{mv_1^2}{2} - \frac{GMm}{r_1} = \frac{mv_2^2}{2} - \frac{GMm}{r_2}
mv122−GMmr1=mv222−GMmr2\frac{mv_1^2}{2} - \frac{GMm}{r_1} = \frac{mv_2^2}{2} - \frac{GMm}{r_2}

Menenie Ap / Pe

Celkovo dostávame

r_a = \frac{r_p}{\left( \frac{2GM}{r_pv_p^2}\right) - 1}
ra=rp(2GMrpvp2)−1r_a = \frac{r_p}{\left( \frac{2GM}{r_pv_p^2}\right) - 1}

Menenie orbitálnej inklinácie

Rendezvouz

Časť 4: We choose to go to the Minmus

Hohmann transfer

Free-return trajectory

Časť 5: Liftoff, touchdown

Suicide burn

  • Vznášanie plytvá palivo

 

  • Raketa vykonáva spomalený pohyb
  • Brzdnú dráhu vieme zrátať
    • Nezabudnime, že rakete sa mení hmotnosť

Presné pristátie

  • Periapsa nad cieľom
  • Zastavíte nad ním
    • Pozor na terén
  • Jemné korekcie

Vzlet k priamemu stretnutiu

  • Efektívny vzletový profil na orbitu
    • Vieme zrátať, koľko nám to bude trvať
  • Chceme, aby stanica skončila tam kde my

Let atmosférou

  • Odpor vzduchu vs gravitácia
  • Horizontal vs vertical
  • Uhol vletu do atmosféry
    • Plytký: nezabrzdíte
    • Strmý: BURN!

Let atmosférou

Časť 6: These are the voyages of SS Lazyness

Oberthov efekt

Aerobraking

Otázky?

Jakub Havelka    Adam Dej

Ďakujeme za pozornosť

Made with Slides.com