Adam Glos
Optimality of quantum strategy for CHSH game
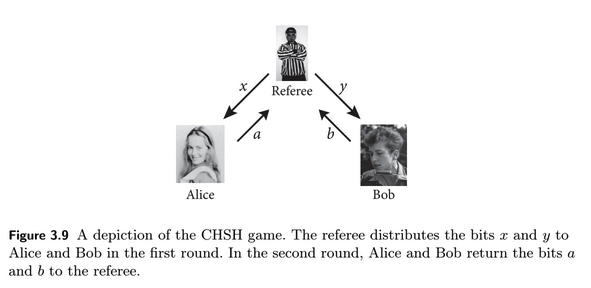
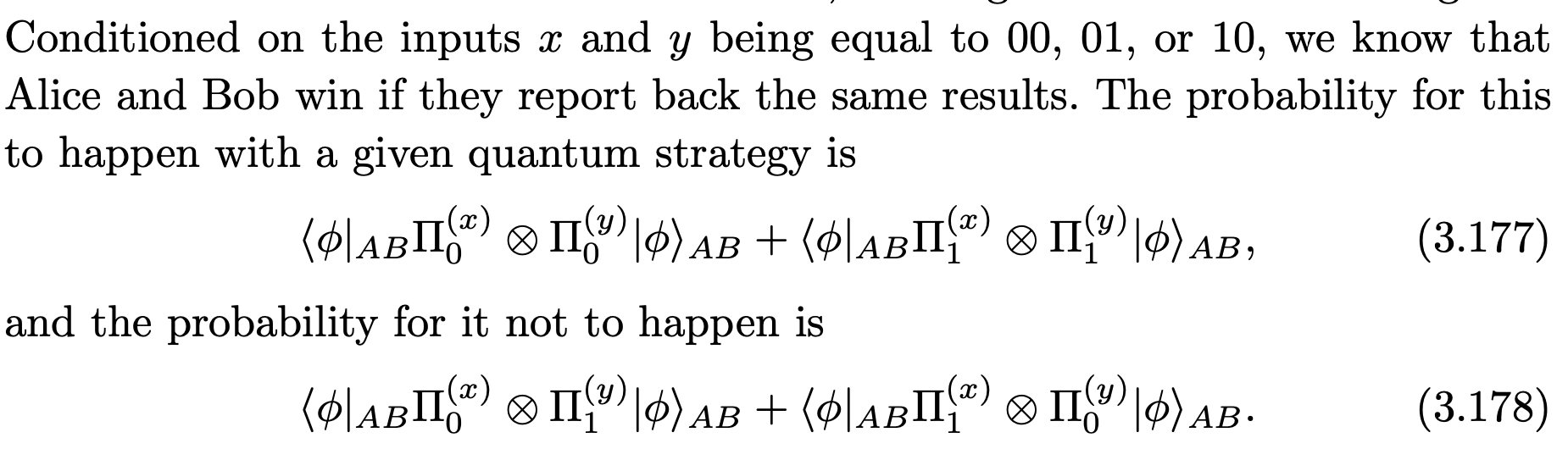

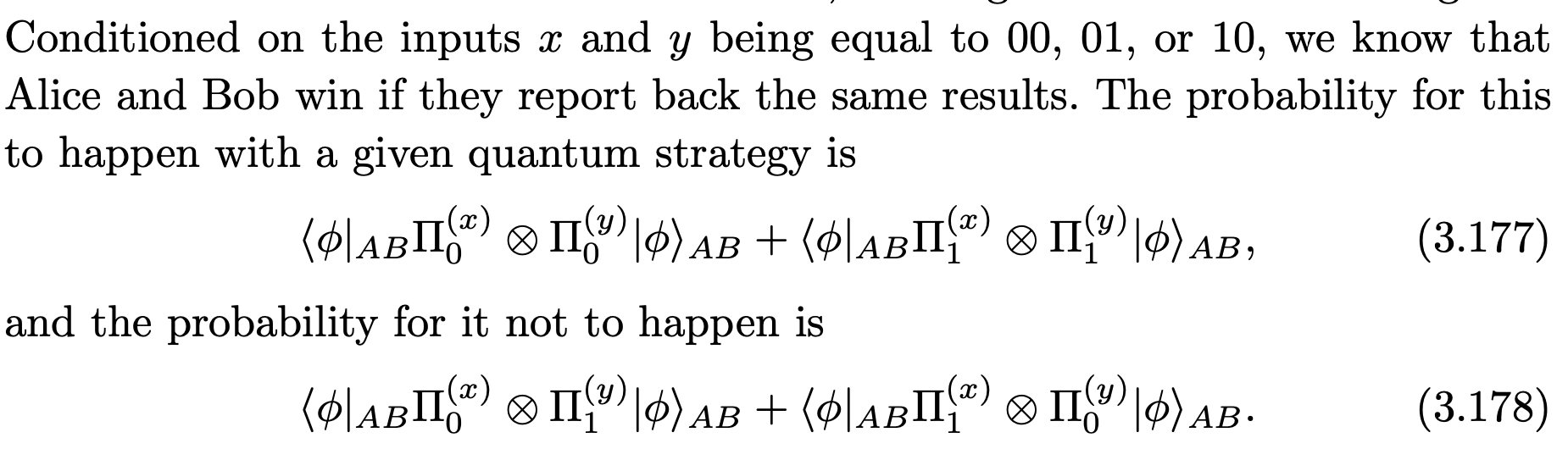
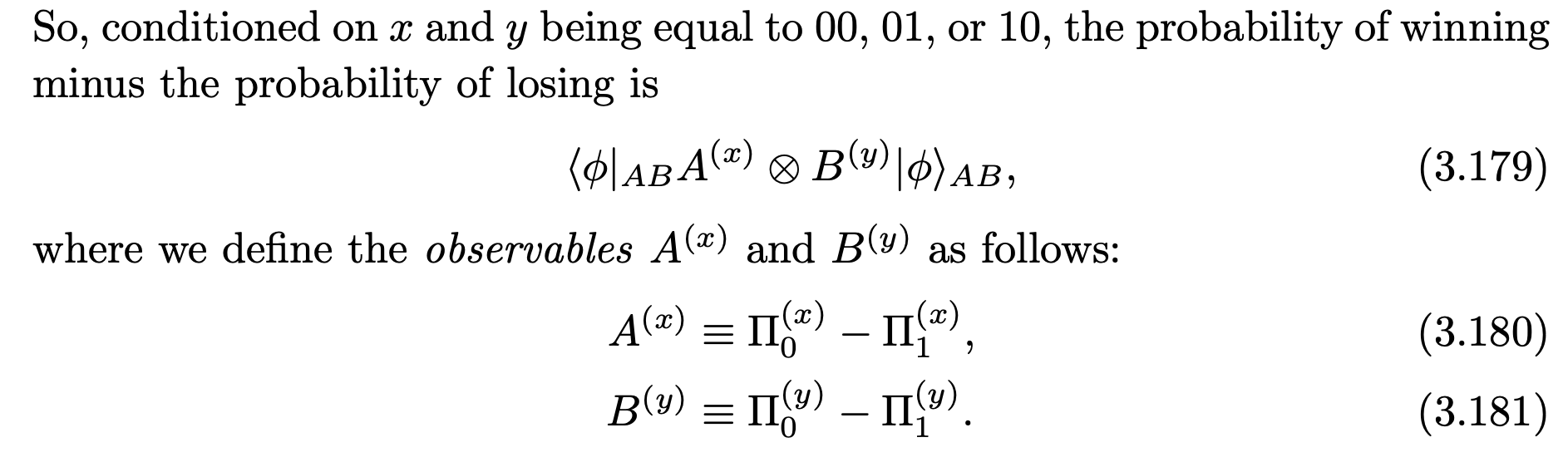
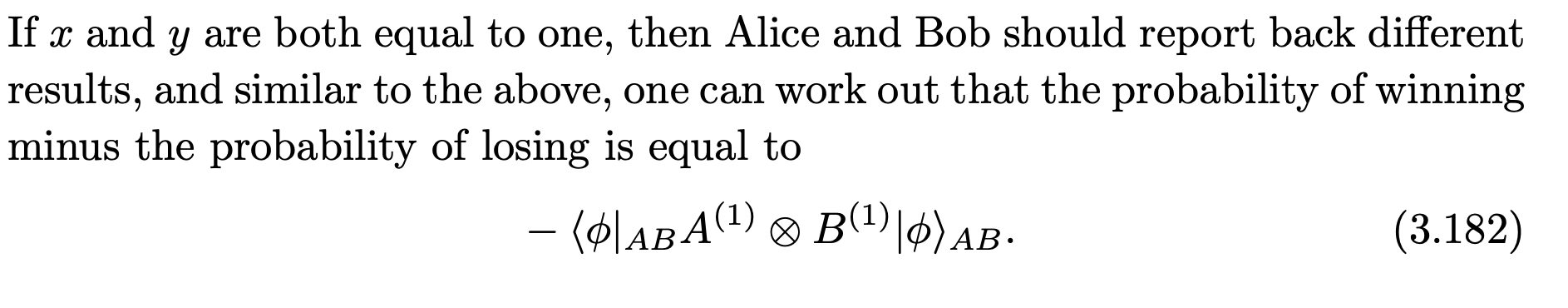

We loose in the opposite scenario, hence minus
sum those two to get observable!

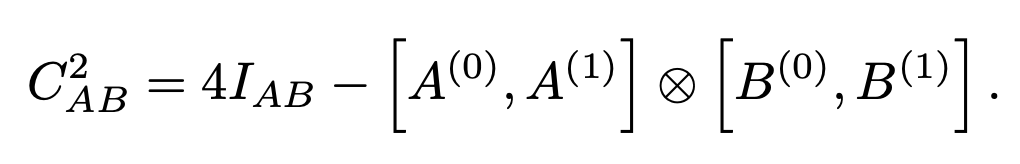
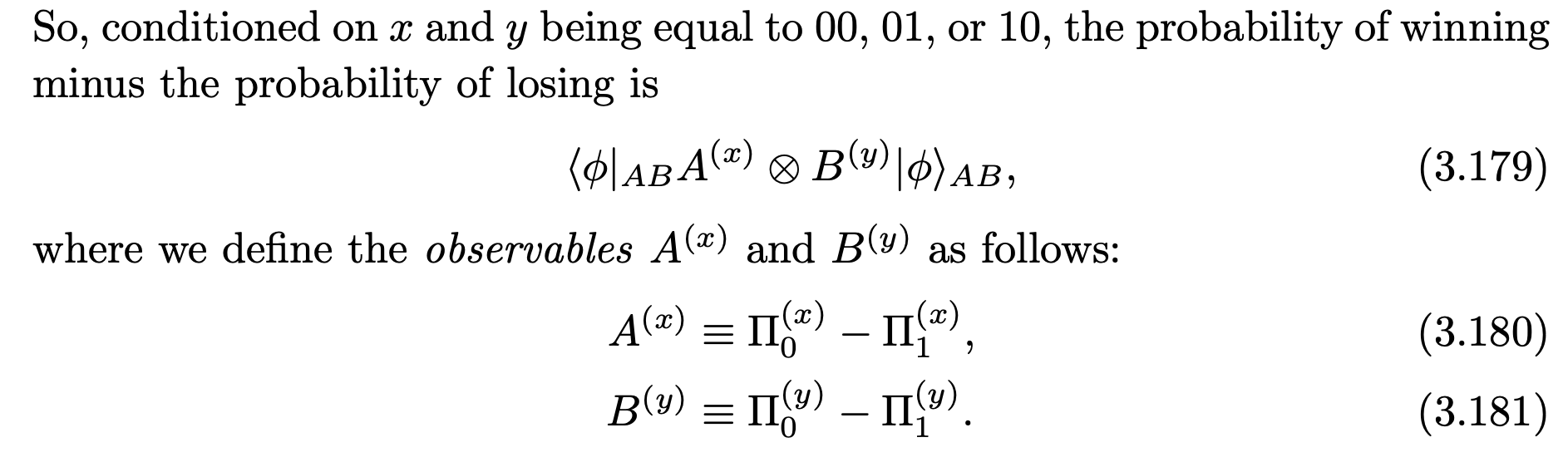
(A^x)^2 = (\Pi_0 -\Pi_1)^2 = \Pi_0^2 + \Pi_1^2 - \Pi_0 \Pi_1 -\Pi_1 \Pi_0
= \Pi_0 + \Pi_1 - 0 - 0 = I
(B^x)^2 = I
(A^0 \otimes B^0) (A^0 \otimes B^1) = I \otimes (B^0B^1)
if both same - identity (x4)
(A^1 \otimes B^0) (-A^1 \otimes B^1) = -I \otimes (B^0B^1)
if one same - cancel out
The rest will form comutator -part
Infinity norm
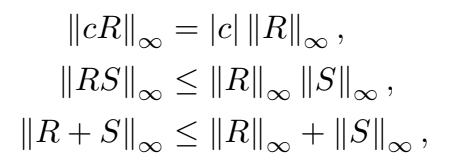
\|A\| = \max_{|\psi \rangle} \langle \psi | A^TA |\psi \rangle
\|I\| = \max_{|\psi \rangle} \langle \psi | I^T I |\psi \rangle = \max_{|\psi \rangle} \langle \psi | \psi \rangle = 1
\|\Pi_0 -\Pi_1\| = \max_{|\psi \rangle} \langle \psi | ( \Pi_0 -\Pi_1)(\Pi_0 -\Pi_1) |\psi \rangle
= \max_{|\psi \rangle} \langle \psi | \Pi_0 + \Pi_1|\psi \rangle
\leq \max_{|\psi \rangle} \langle \psi | I|\psi \rangle = 1
Infinity norm - Kronecker Product
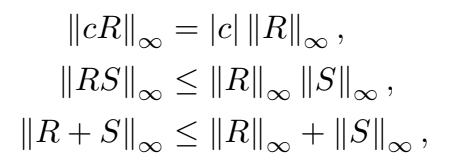
\|A\| = \max_{|\psi \rangle} \langle \psi | A |\psi \rangle
\|A \otimes B\| = \|(A \otimes I)(I \otimes B ) \| \leq \|A \otimes I \| \|I \otimes B \|
\|A \otimes I\| = \|A\|
this is maximum squared eigenvalue
Eigenvalues of \(A \otimes I\) are the same as \(A\) but multiplied
A\otimes I = UD_AU^\dagger \otimes I = (U\otimes I) (D_A\otimes I) (U^\dagger \otimes I)
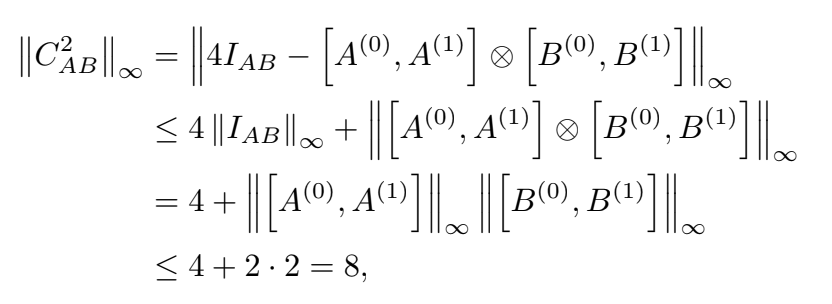
1
2
3
4
1. definition
2. norm of sum
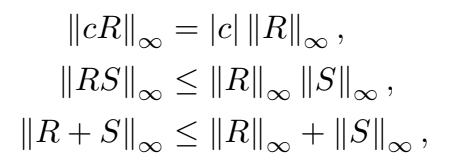
3. norm of identity is one and norm of kronecker product
\|I\| = 1
4.
\|[A^0,A^1]\| = \|A^0A^1 - A^1A^0\| \leq \|A^0A^1 \| + \| A^1A^0\| \leq 2\|A^0\| \|A^1 \|
\|A^0\| = \|\Pi_0^0 - \Pi_1^0\| \leq 1
\|A\otimes B\| = \|A\|\|B\|
