Project proposals
Adam
August 2021
Method of continuation for QAOA
The problem: It is difficult to optimize QAOA when there are many levels.
- Optimize the whole circuit with m levels from randomly chosen 2m angles (bad approach)
- Optimize the circuit for m-1levels, fix the angles and then optimize for m-th level. Repeat recursively (bad approach)
- Optimize the circuit for m-1 levels, and then add two angles (based on some strategy) and optimize 2m angles again. can be improved by adding different two angles several times and choosing the best one
- other methods (investigate)
Method of continuation for QAOA, cont.
New proposal
- Choose somehow a large \(m\)
- use the same circuit as for QAOA with mixer \(H_1\) and objective Hamiltonian \(H_2\)
- \(\theta_0\) - random angles of length \(2m\)
-
for \(a = a_0, a_0 + \epsilon , a_0 + 2\epsilon , ..., 1\),
- get optimal angle \(\theta_{\rm opt}\}\) of the circuit according to objective Hamiltonian \((1-a) H_1 + a H_2\) starting with \(\theta_0\)
- \(\theta_0 \leftarrow \theta_{\rm opt}\)
- \(\theta_0\) is the optimal angle.
Method of continuation for QAOA, cont.
Motivation
- method of continuation (?) is a classical algorithm which starts in the solution of a simple problem and gradually change it to a solution of the harder problem
- At extreme case \(a = 0\) the optimal solution is (0,0,...,0) for objective Hamiltonian and arbitrary for mixer Hamiltonian. Hence for a close to 0 it should be simple to found a solution
- Some motivation from adiabatic theorem??
Method of continuation for QAOA, cont.
Research problems
- Can we, with the same number of layers, achieve lower energy states?
- If not, can we reach it faster?
- What are good choices of \(a_0\) (initial value) and \(\epsilon\) (step values)?
- We should consider different optimizers (L-BFGS, Nelder-Mead, etc.)
- We can restrict ourselves to Max-Cut only (this may give us some scaling
- We should investigate whether something like this was not done yet
Thoughts
Almost optimal TSP Hamiltonian implementation
Quality measures of the encoding/implementation
- number of qubits (noise)
- the number of gates (noise)
- the depth of the circuit (noise, time complexity)
- number of measurements (time complexity)
- number of parameterized gates (time complexity for gradient-based methods)
- size of the effective space (time complexity/solution quality)
Secondary quality measures
- volume
- the difference of maximal and minimal energy
Almost optimal TSP Hamiltonian implementation
Minimal requirements for TSP for n cities
- number of qubits: \(O(n \log n)\)
- the number of gates: \(O(n^2)\)
- the depth of the circuit: \(O(n^2/(n \log n))=n/\log n\)
- number of measurements: \(n (\max_{i\neq j} W_{ij} - \min_{i\neq j} W_{ij})\) seems to be realistic, probably just \(O(n)\) for \(\max_{i,j}W_{ij} = O(1)\)
- number of parameterized gates: \(O(n^2)\) seems realistic
- size of the effective space: O(n!), also \(O(n^n)\) makes sense
Difference between \(O(n^n)\) and n! is only in \(O(\exp(n))\) which can be saved in \(O(n)\) qubits. This is why I consider \(n^n\) to be almost optimal
Almost optimal TSP Hamiltonian implementation
| QAOA | XY-QAOA | GM-QAOA | HOBO | |
|---|---|---|---|---|
| No. qubits | n^2 | n^2 | n^2 | n log(n) |
| No. gates | n^3 | n^3 | n^3 | n^4 |
| depth | n | n | n or n^2 | n^3 |
| Energy span | n^3 | n^3 | n^3 or n | n^2 |
| No. of param. gates | n^3 | n^3 | n^3 | n^4 |
| size of the effective space | 2^(n^2) | n^n | n^n or n! |
n^n |
QAOA is worse in any aspect
NEW ENCODING
| NEW | XY-QAOA | GM-QAOA |
HOBO | |
|---|---|---|---|---|
| No. qubits | n log n | n^2 | n^2 | n log(n) |
| No. gates | n^2log^2 n | n^3 | n^3 | n^4 |
| depth | n log(n) | n | n or n^2 | O(n^3) |
| Energy span | n | n^3 | n^3 or n | n^2 |
| No. of param. gates | n^2 | n^3 | n^3 | n^4 |
| size of the effective space | n^n | n^n | n^n or n! |
n^n |
Green if optimal (up to polylog) - HAS TO BE CHECKED IF TRUE!
Similar work for Max-K-Cut: https://doi.org/10.1007/s42979-020-00437-z . Seems to be worse in many contexts
New encoding
The Hamitlonian
- \(A_1\), \(A_2\) are penalty parameters
- \([\varphi]\) is Iverson notation which gives one i \(\varphi\) is true, and zero otherwise
- \(H_{\rm route\ cost}\) is a Hamiltonian which for valid \(b\) gives cost of the route
\([b\ \rm is\ permutation]\)
- Let \(|b_1\rangle, \dots, |b_n \rangle\) be quantum registers for encoding cities in a binary way
-
Let \(|\#1\rangle,\ldots,|\#n\rangle \) be quantum registers which will store numbers of \(1,\dots, n\) in previous register
- for all \(b_i\) we add +1 to \(|\#k\rangle\) if city \(k\) is encoded in \(b_i\). This can be done through (easy to parallelize)
- storing the output of "is \(k\) in b_i" through "Toffoli" on a separate ancilla qubit \(|flag_i\rangle\)
- if the \(|flag_i\rangle\) is 1, then add 1 to \(|\#k\rangle\), then clean \(|flag_i\rangle\)
- Apply XOR 1 on all \(|\# k\rangle\), and then NOT everywhere on it
- Apply Toffoli conditioned on all \(|\#1\rangle, \dots,|\#n\rangle\) with output on \(|FLAG\rangle\)
- Rotate \(|FLAG\rangle\) by \(R_z(\theta_i A_1)\)
- uncompute 1.-4.
It's like in Grover, but with rotation except of \(Z\) gate
\([b\ \rm is\ permutation]\) (analysis)
- \(O(n\log n)\) ancilla qubits required
- \(O(n^2 {\rm poly}(\log n))\) gates (to be confirmed)
- \(O(n\log n)\) depth (to be confirmed)
Parallelization: we have to make (or not) addition for each pair \((b_t, \#k)\). However this can be done as follows: first all pairs \((b_i,\#i)\), then \((b_i,\#(i+1))\), etc.
\([b_t\ \rm is\ valid]\)
Cone be done as in paper of me, Zoltan and Ola, which gives already \(O(n)\) complexity, but we can already start in \(\sum_{x=0}^{n-1}|x\rangle\) (obviously tensored to \(n\)-th power)
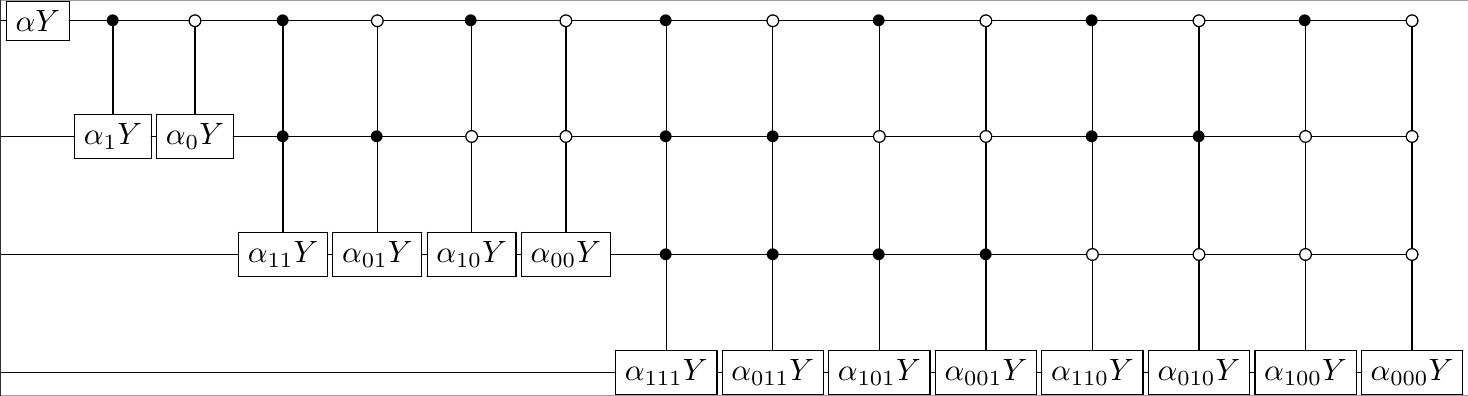
With proper choice of \(\alpha_{?}\) we should be able to generate any real-valued superposition
\(\log n-2\) ancilla qubits, \(O(n)\) depth, \(O(n {\rm poly}(\log n))\) no. gates
Then we can use GM-like oracle applied \(|b_i\rangle\)-wise and drop the space to \(n^n\)
Cost Hamiltonian (check!)
- Let \(|b_1\rangle, \dots, |b_n \rangle\) be quantum registers for encoding cities in a binary way
-
Let \(|\#1\rangle,\ldots,|\#n\rangle \) be quantum registers which will store numbers of \(1,\dots, n\) in previous register
- for all \(b_i\) we add +1 to \(|\#k\rangle\) if city \(k\) is encoded in \(b_i\). This can be done through (easy to parallelize)
- storing the output of "is \(k\) in b_i" through "Toffoli" on a separate ancilla qubit \(|flag_i\rangle\)
- if the \(|flag_i\rangle\) is 1, then add 1 to \(|\#k\rangle\), then clean \(|flag_i\rangle\)
-
For each pair \((\#k, \#m)\) (can be parallelized)
- save the flag of "both are ones" to \(|FLAG\rangle\)
- Rotate \(|FLAG\rangle\) by \(R_z(\theta_i W_{k,m})\)
- all but \(R_z\) rotation
This is less demanding version of permutation checking
Why this is interesting
- We created an objective Hamiltonian simulation which is "almost the best of them all in every context I know"
- It should give the same quality per layer as HOBO (which was the best of all I know), perhaps even better
- The Hamiltonian-way encoding cannot reach such good quality measures values ("proof": if we want to encode the Hamiltonian in a way that we have different register for different timepoints, then between each pair of such registers we have to include whole information about \(W\), which results in \(O(n^3)\) gates in total (as we have \(n^2\) values in \(W\) and \(n\) pairs))
Questions two answer
- What is the exact form of Hamiltonian (cost route part not obvious)
- What about not-full connectivity of the hardware (linear or square) can we say something?
- Can we extend this to other algorithms? Max-k-Cut, VRP, job scheduling etc.