Space-efficient binary optimization for variational computing
Adam Glos
Institute of Theoretical and Applied Informatics, Polish Academy of Sciences

Overview
Introduction to NISQ era quantum
combinatorial optimization
Making problems quantum accesible - QUBO and Ising model
Something more - HOBO
Future ideas?
The problem: TSP
given the cost between each cities, find the cheapest route such that the route goes through all cities and comes back
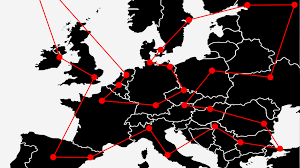
We need short, mathematical, and general description
Integer programming?
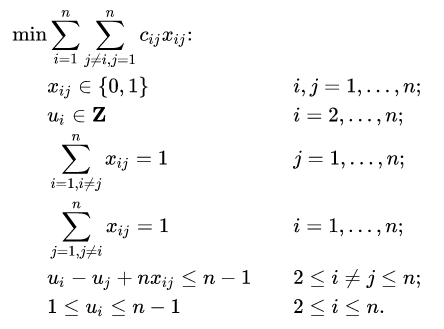
Binary optimization
where all variables are bits


Since every number can be represented by bits...
0-1 integer programming is quite general!
Quadratic Unconstrained Binary Optimization
Any NP-complete problem can be turned into QUBO
Every binary function can be turned into quantum polynomial, but not necessarily quadratic!
Lucas, Andrew. "Ising formulations of many NP problems." Frontiers in Physics 2 (2014): 5.

Ising model
Instead of 0-1, we have now -1/1
If HOBO model has finite order, then it is small AND corresponding Ising model is small
This is not always true for higher order models
QUBO is transformed to 2-local Ising model
Quantum optimization algorithms
Quantum annealing

Different input for each algorithm!
Variational optimization (VQE, QAOA)


Quantum annealing


- Must be QUBO (quadratization sometimes needed)
- many (qu)bits needed
- graph embedding required
Variational Quantum Eigensolver
- Can be a general binary optimization - we only need an efficient procedure for calculating energy!
- just walking on a Hilbert space...
- ansatz-dependent
- designed for harder problems

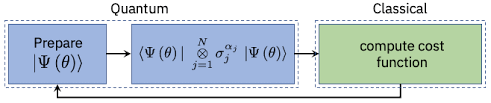
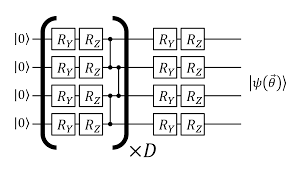
Peruzzo, Alberto, et al. "A variational eigenvalue solver on a photonic quantum processor." Nature communications 5.1 (2014): 1-7.
QAOA - a special VQE
Unlike VQE, we have to implement the objective Hamiltonian
Still we can use higher order terms!
|
Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. "A quantum approximate optimization algorithm." arXiv preprint arXiv:1411.4028 (2014). |
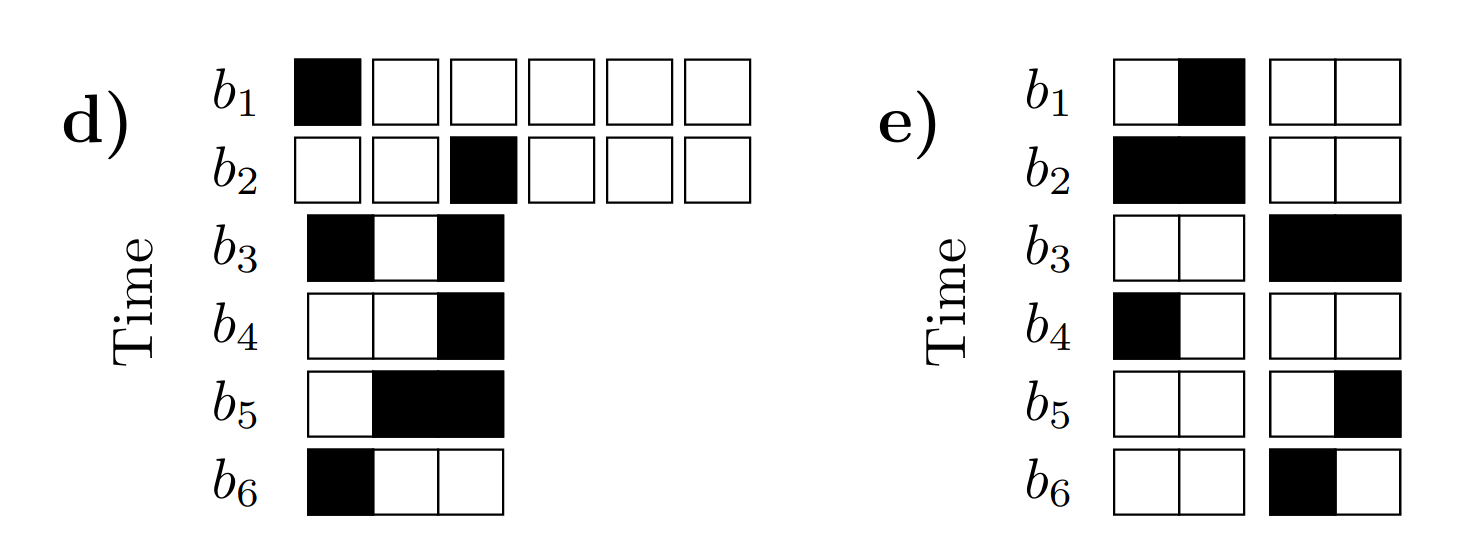
TSP - waste of qubits
We have n! possible routes



only N log(N) qubits!
QAOA - can we run it?
We have to implement the objective Hamiltonian
QAOA - can we run it? cont.
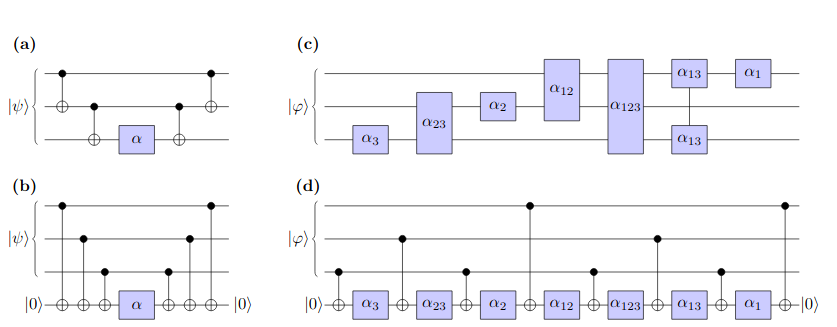

QAOA - can we run it? cont.
For QUBO we need O(N) depth, for HOBO O(N^3) - much worse!
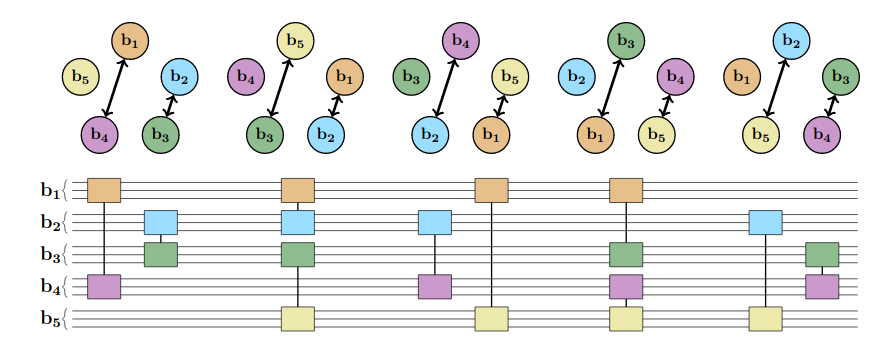
Is HOBO better?
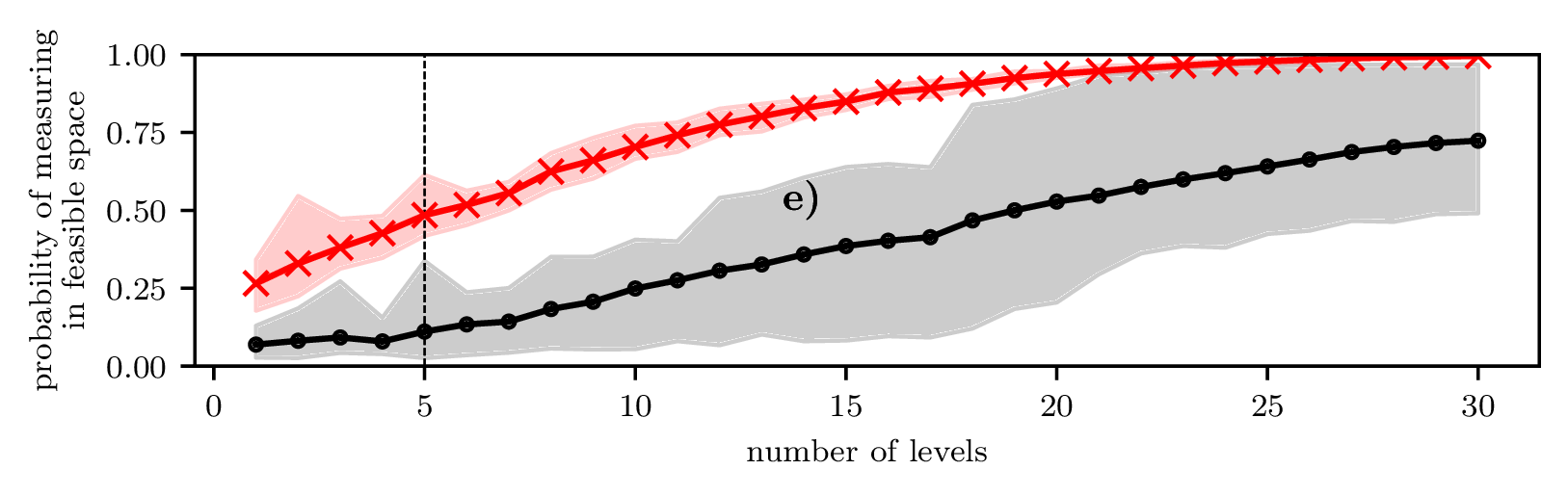
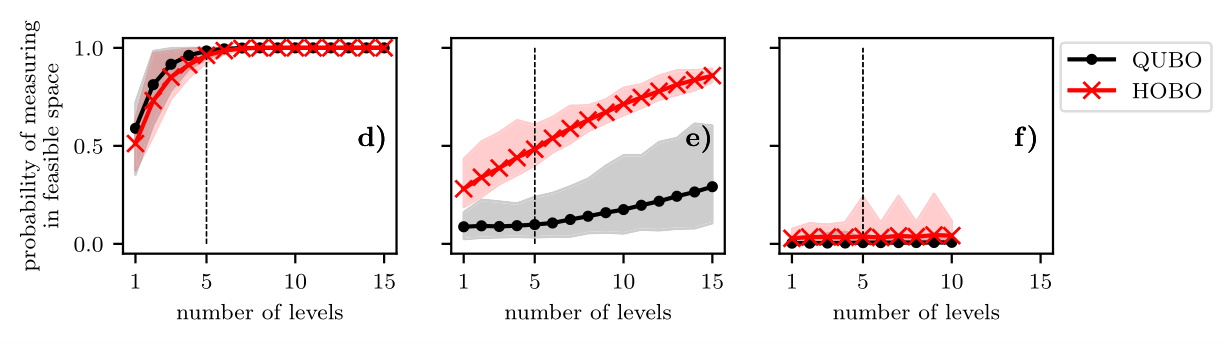
N=3
N=4
N=3
N=5
N=4
Alternative approach - mixed
Text
Conclusions
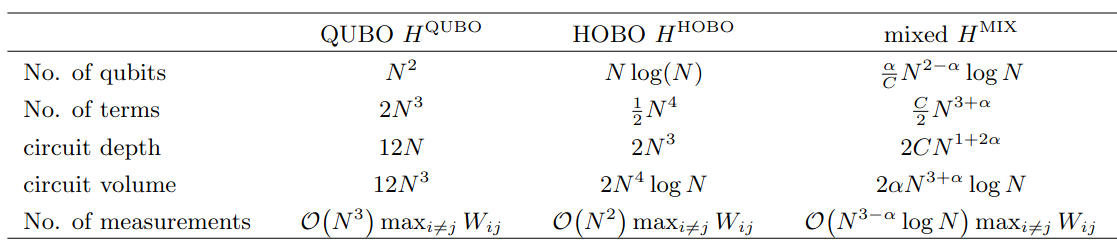
We have developed an encoding, which
- uses smaller number of qubits,
- may be more efficient than QUBO,
- has smaller relative feasible space,
- produces much longer circuits than QUBO!
Glos, A., Krawiec, A., & Zimborás, Z. (2020). Space-efficient binary optimization for variational computing. arXiv preprint arXiv:2009.07309.
New idea !
HOBO-size mixer
Change of the encoding (from binary to one-hot vector at inverse)
QUBO objective encoding