QAOA - the project
HOBO vs QUBO
deep but not so much qubits
short, but many qubits
QUBO
HOBO
Why is HOBO interesting?
- Uses less qubits,
- By this feasible space takes most of the space
Q: How many of bit assignments are feasible one (proper routes) for TSP?
QUBO:
HOBO:
We spend less time on finding feasible space, which we can use on optimizing the solution
This is not that simple

Solution: change the encoding (all the time)
HOBO requires much deeper circuits.
But can we benefit from reducing the feasible space, even w/o the improvement on the number of qubits?
The idea
HOBO-size mixer
Change of the encoding (from binary to one-hot vector at inverse)
QUBO objective encoding
Quality measures
- Number of qubits is the number of the worst encoding
- Depth is equal to sum of depths of each part
- Number of measurement is tricky is as for objective Hamiltonian
depth
How to transform encoding?

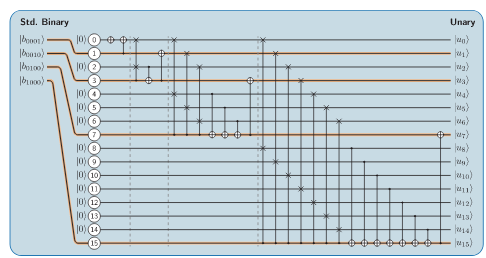
First bunch of tasks
- Implement quantum circuit for QUBO (use parallelism)
- implement encoding transformation (binary to unary)
- make notes
- prove it works (should be simple)
- compute the depth of the circuit (up to constant)
- determine no. measurements


Test if QAOA works!
Simplifications

Change of the encoding is a permutation, but because of we do uncomputation, we can do it up to local phases
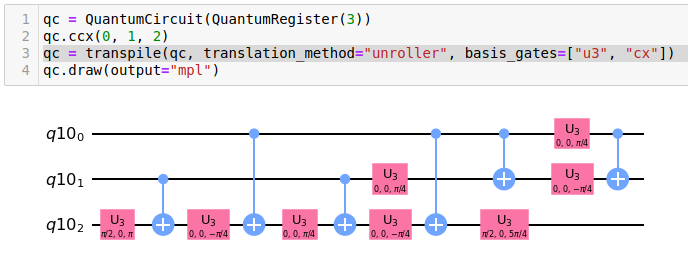
Depth 11
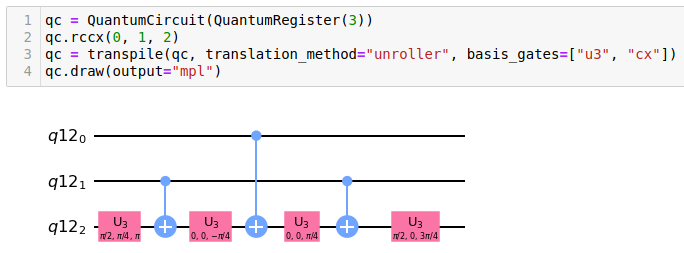
Depth 7
Mixing objective Hamiltonian
Part of objective Hamiltonian in HOBO
Part of objective Hamiltonian in QUBO
Q: What is the objective Hamiltonian? probably sum of them
Affects depth and no. of measurements
Starting in W-state
Q: How to generate W-state?
Problem with mixer Hamiltonian - how to define such?
Automatic testing
We can make measurement to test, whether we still are at right place, and continue if only 0s are measured
Q1: Does it give any benefits? - test by simulation
Q2: Does it improve anything? - assumption on the strength of the noise
Q3: error correction?
Tools
- git (probably GitHub for now)
- Anaconda + Python + qiskit, or
- Julia + Yao
- TeX