Optimal QAOA design for the
Traveling Salesman Problem
Bence Bakó, Adam Glos, Özlem Salehi, Zoltán Zimborás

QAOA
- Used for combinatorial optimization
- Natively for gate-based model
- encodes the problem into the circuit
$$|p,r\rangle = \prod_{i=1}^k \exp(-\mathrm{i} p_iH_{\rm mix})\exp(-\mathrm{i} r_iH) |+^n\rangle $$
- \(p_i\) and \(r_i\) optimized by external classical procedure
- Since the problem is encoded into the circuit - how to minimize resources needed?
Quality measures
- number of physical qubits
- effective space size
- number of gates
- number of parameterized gates
- depth
- depth on LNN
- energy span
No. qubits and effective space size
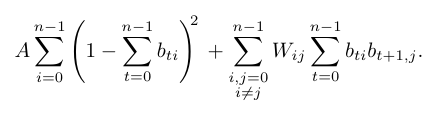
XY-QAOA for TSP
mixer: \(X_iX_j + Y_iY_j\)
- \(n^2\) qubits are needed
- with good mixer, only one hot states are present (for example \(|001\rangle |010\rangle |001\rangle\))
- There is only \(n^n\) of them
- effective space space size is \(\log(n^n) = n\log n\)
- both lower bouned by log of the number of solutions
No. (parameterized) gates
- ZZZ applied
- 5 gates, but 1 parameterized gates
- The larger number of gates - the more destructive noise
- number of parameterized gates may influence the cost of estimating analytical gradient.
- both lower bounded by the number of degrees of freedom in the problem (for example number of possible edges in Max-K-Cut)
\(H = - \sum_{i,j}w_{i,j}Z_i Z_j - \sum_i w_i Z_I\)
Depth (on LNN)
- we assume parallel computation
- two cases: all-to-all connectivity and LNN connectivity
- lowerbounded by number of gates over number of qubits
Energy span
- Difference between maximal and minimal achievable energy
- influences the number of measurement required for the energy estimation
From Hoeffding Theorem
Better than the state-of-the-art way for VQE
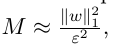
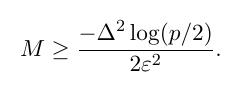
\(H = - \sum_{i,j}w_{i,j}Z_i Z_j - \sum_i w_i Z_I\)
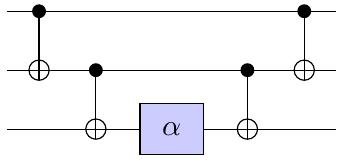
Minimal example
- Hamiltonian \(H = -\prod_{i=1}^n b_i\)
- Corresponding Ising model: \(H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)\) exponential number of terms!

Alternative

\(O(n^2)\) gates on LNN!
\(b_i \leftarrow \frac{1-s_i}{2}\)
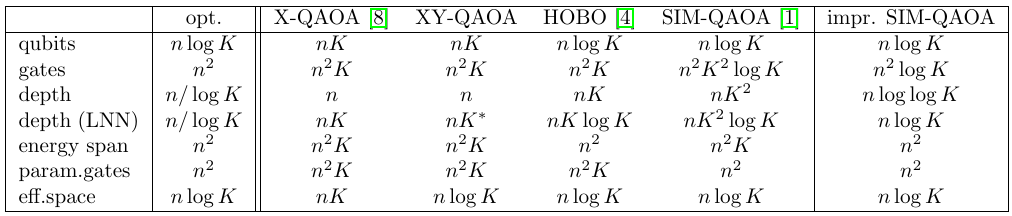
SIM-QAOA
Max-K-Cut

- Graph as an input
- \(K\) colors
- maximize number of edges connecting different colors
Max-K-Cut
- X-QAOA - X mixer, standard QUBO,
- XY-QAOA - XY mixer, standard QUBO
- HOBO - binary encoding, X-mixer
- Fuchs-QAOA - as in Fuchs, Franz G., et al. "Efficient Encoding of the Weighted MAX-k-CUT on a Quantum Computer Using QAOA." SN Computer Science 2.2 (2021): 1-14.
At least one cost depends siginificantly on K
Fuchs-QAOA
Fuchs-QAOA
Very bad when \(K=2^k+1\)

- All colors have meaning - last color is multiplied
- Fix incorrectly assumed different colors


Fuchs-QAOA
Max-K-Cut - SIM-QAOA

- we start in product of W-like state in a binary encoding
- quantum version of the classical pseudocode,
- Dependency on K basically disappeared

Fuchs-QAOA
Was it interesting?
YES
NO
- we reached optimal quality measures
- we essentially dropped the dependency on \(K\)
- Fits very well NISQ requirements!
- we essentially took Fuchs idea and have simply chosen better initial state...
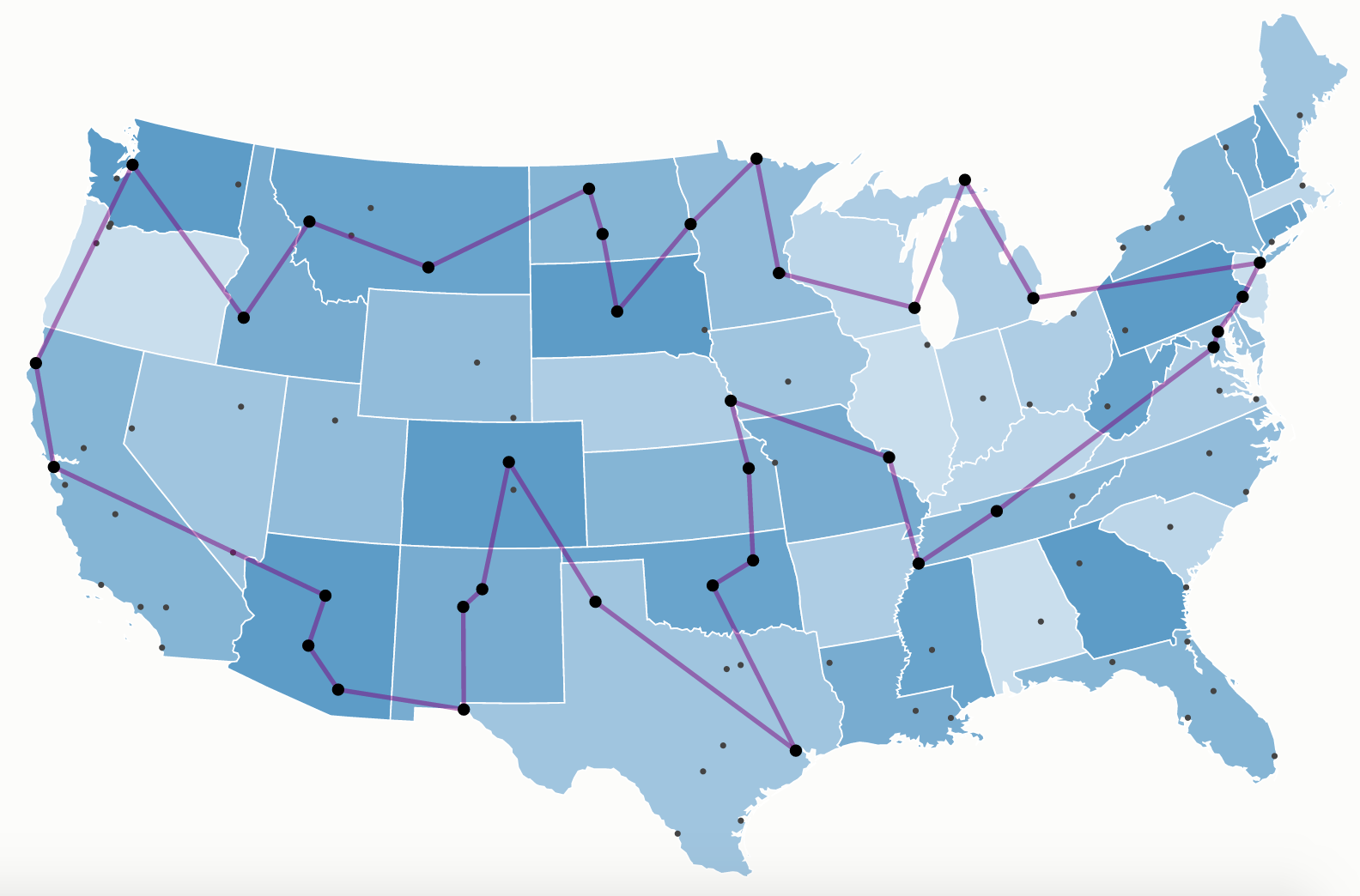
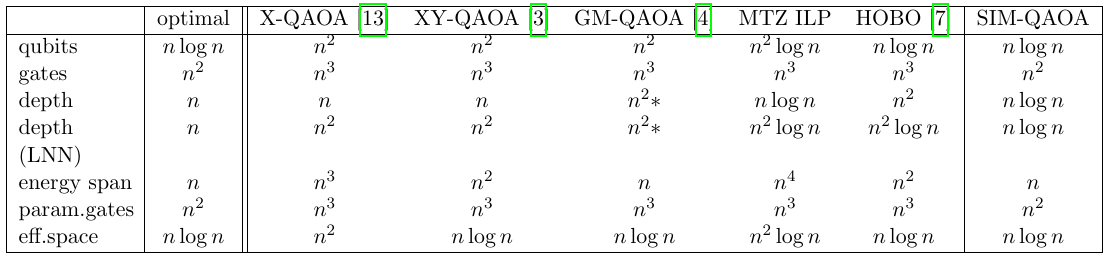
TSP
$$ A\sum_{t} \left(\sum_v b_{tv} -1\right)^2 + A\sum_{v} \left(\sum_t b_{tv} -1\right)^2 + B\sum_{t} \sum_{v,w} W_{v,w}b_{t,v}b_{t+1,w}$$
TSP
-
None of the encodings matches the "natural optimal" value, ...
-
..., but none can! Each red block needs whole information about cost matrix - \(O(n^3)\) gates

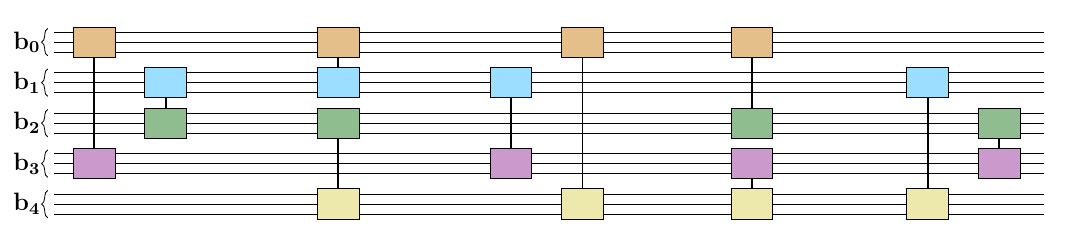
SIM-QAOA for TSP
- We start in the superposition of valid cities for each time-point
- we choose Grover Mixer for our purpose (different ones can be used)
- Hamiltonian implemented through a quantum version of the classical pseudocode (with some parallelization + swapping strategy)
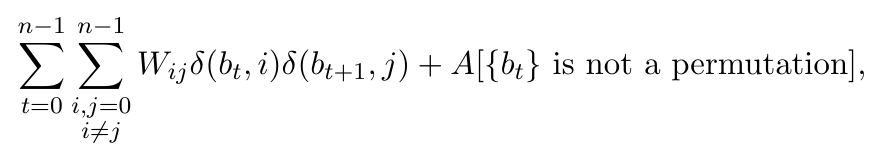
TSP - SIM-QAOA


TSP - SIM-QAOA

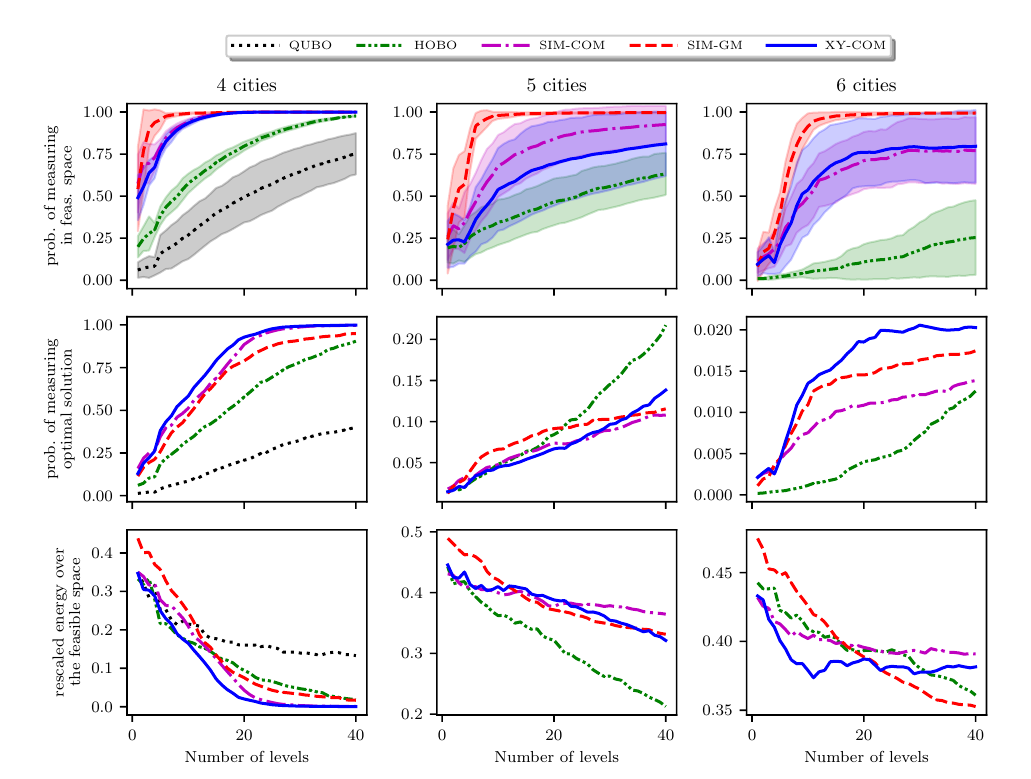
TSP - numerics
Generalization
The idea can be generalized, so far we managed to use it for
- Set Cover problem
- Integer Linear Problem (trade-off)
- Graph Isomorphism (trade-off in general, optimal for Euclidean graphs)