SIM-QAOA
Bence Bakó, Adam Glos, Özlem Salehi, Zoltán Zimborás
Quality measures
- number of physical qubits
- effective space size
- number of gates
- number of parameterized gates
- depth
- depth on LNN
- energy span
No. qubits and effective space size
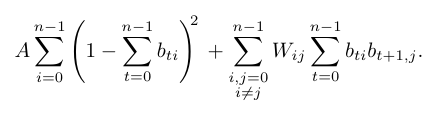
XY-QAOA for TSP
mixer: \(X_iX_j + Y_iY_j\)
- \(n^2\) qubits are needed
- with good mixer, only one hot states are present (for example \(|001\rangle |010\rangle |001\rangle\))
- There is only \(n^n\) of them
- effective space space size is \(\log(n^n) = n\log n\)
- both lower bouned by log of the number of solutions
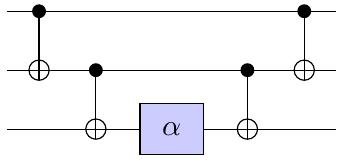
No. (parameterized) gates
- ZZZ applied
- 5 gates, but 1 parameterized gates
- The larger number of gates - the more destructive noise
- number of parameterized gates influences the cost of estimating analytical gradient.
- both lower bounded by the number of degrees of freedom in the problem (for example number of possible edges in Max-K-Cut)
Depth (on LNN)
- we assume parallel computation
- two cases: all-to-all connectivity and LNN connectivity
- lowerbounded by number of gates over number of qubits
Energy span
- Difference between maximal and minimal achievable energy
- influences the number of measurement required for the energy estimation
From Hoeffding Theorem
Better than the state-of-the-art way for VQE
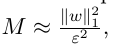
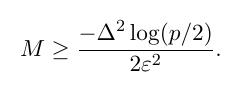
Max-K-Cut
- X-QAOA - X mixer, standard QUBO,
- XY-QAOA - XY mixer, standard QUBO
- HOBO - binary encoding, X-mixer
- SIM-QAOA - as in Fuchs, Franz G., et al. "Efficient Encoding of the Weighted MAX-k-CUT on a Quantum Computer Using QAOA." SN Computer Science 2.2 (2021): 1-14.
At least one cost depends siginificantly on K
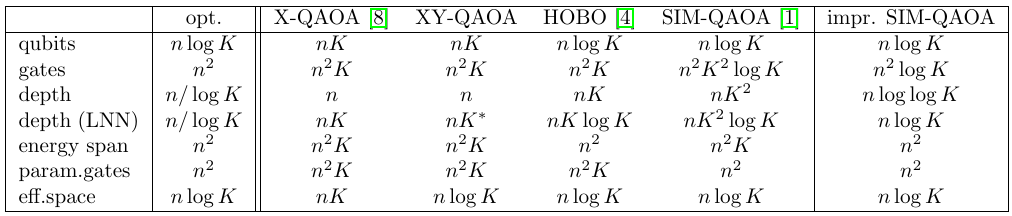
Max-K-Cut - SIM-QAOA
Very bad when \(K=2^k+1\)

- All colors have meaning - last color is multiplied
- Fix incorrectly assumed different colors


Max-K-Cut - SIM-QAOA

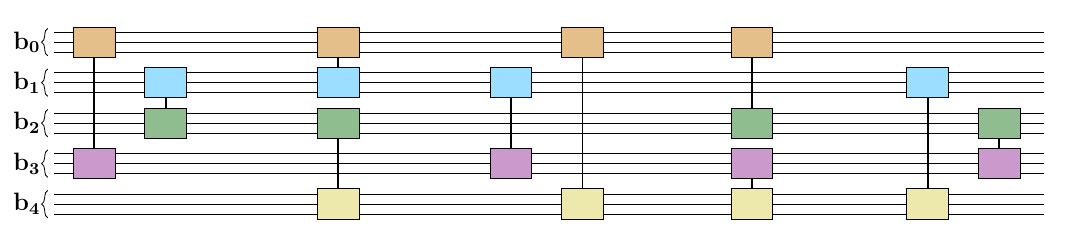
- we start in product of W-like state in a binary encoding
- quantum version of the classical pseudocode,
- for double loop: use swap network
- Dependency on K basically disappeared

TSP
None of the encodings matches the "natural optimal" value
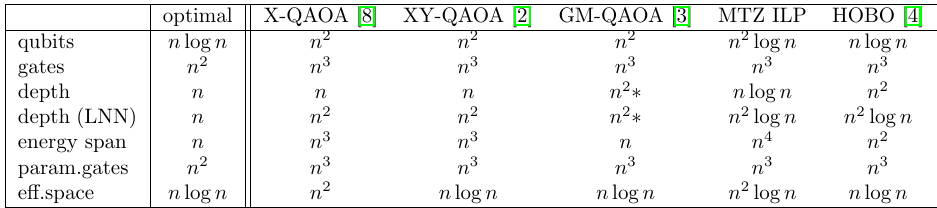
number of qubits times depth at least \(O(n^3)\) for
TSP - SIM-QAOA
- We start in binary encoding like in HOBO (product of \(n\) W-state-like states in binary encoding
- we choose Grover mixer for our purpose (different ones can be used)
- Hamiltonian implemented through a quantum version of the classical pseudocode (with some parallelization + swapping strategy)
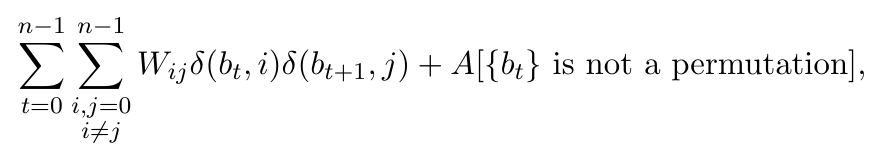
TSP - SIM-QAOA


TSP - SIM-QAOA

The idea can be generalized, so far we managed to use it for
- Set Cover problem
- Integer Linear Problem (trade-off)
- Graph Isomorphism (trade-off in general, optimal for Euclidean graphs)