Cotraining for Diffusion Policies

Oct 25, 2024

Adam Wei

Congratulations Dr. Terry Suh!

🎉

🎉

It's ok Terry :(

PhD

❌

Start Up

✅

Screw the PhD...

 

Mr. Suh sounded better anyways...

Agenda

  1. Motivation
  2. Cotraining & Problem Formulation
  3. Vanilla Cotraining & Insights
  4. Algorithms for cotraining
  5. Future Work

Motivation: Sim Data

Sim Infrastructure

Sim Data Generation

Motivation: Sim Data

  • Simulated data is here to stay => we should understand how to use this data...
  • Best practises for training from heterogeneous datasets is not well understood (even for real only)

Octo

DROID

Similar comments in OpenX, OpenVLA, etc...

Motivation: High-level Goals

... will make more concrete in a few slides

  1. Empirical sandbox results to inform cotraining practises
  2. Understand the qualities in sim data that affect performance
  3. Propose new algorithms for cotraining

Problem Formulation

\mathcal{D}_{real}

Robot Actions

O

A

\sim p_{real}(O,A)
\sim p_{sim}(O,A)
\mathcal{D}_{sim}

Robot Actions

A

O

Ex: From a human demonstrator

Ex: From GCS

Problem Formulation

\mathcal{D}_{R}

Robot Actions

O

A

\mathcal{D}_{S}

Robot Actions

A

O

  • High quality data from the target distribution
  • Expensive to collect
  • Not the target distribution, but still informative data
  • Scalable to collect

Problem Formulation

\mathcal{D}_{R}\sim p_{R}(O,A)
\mathcal{D}_S\sim p_{S}(O,A)

Cotraining: Use both datasets to train a model that maximizes some test objective

  • Model: Diffusion Policy that learns \(p(A|O)\)
  • Test objective: Empirical success rate on a planar pushing task

Notation

R, S => real and sim

\(|\mathcal D|\) = # demos in \(\mathcal D\)

\(\mathcal{L}=\mathbb{E}_{p_{O,A},k,\epsilon^k}[\lVert \epsilon^k - \epsilon(O_t, A^o_t + \epsilon^k, k) \rVert^2] \)

\(\mathcal{L}_{\mathcal{D}}=\mathbb{E}_{\mathcal{D},k,\epsilon^k}[\lVert \epsilon^k - \epsilon(O_t, A^o_t + \epsilon^k, k) \rVert^2] \approx \mathcal L \)

\(\mathcal D^\alpha\)          Dataset mixture

  • Sample from \(\mathcal D_R\) w.p. \(\alpha\)
  • Sample from \(\mathcal D_S\) w.p, \(1-\alpha\)

Research Questions

  1. For vanilla cotraining: how do \(|\mathcal D_R|\), \(|\mathcal D_S|\), and \(\alpha\) affect the policy's success rate?
  2. How do distribution shifts affect cotraining?
  3. Propose new algorithms for cotraining
    1. Adversarial formulation
    2. Classifier-free guidance

Informs the qualities we want in sim

Vanilla Cotraining

\mathcal L_{\mathcal D^\alpha} = \alpha \textcolor{red}{\mathcal L_{\mathcal D_R}} + (1-\alpha) \textcolor{blue}{\mathcal L_{\mathcal D_S}}

(Tower property of expectations)

Instead:

  1. Choose \(\alpha \in [0,1]\)
  2. Train a diffusion policy that minimizes \(\mathcal L_{\mathcal D^\alpha}\)

Experiments

For vanilla cotraining: how do \(|\mathcal D_R|\), \(|\mathcal D_S|\), and \(\alpha\) affect the policy's success rate?

  • Distributionally robust optimization, Re-Mix, etc
  • Theoretical bounds
  • Empirical approach

Experiment Setup

\(|\mathcal D_R|\) = 10, 50, 150 demos

\(|\mathcal D_S|\) = 500, 2000 demos

\(\alpha = 0,\ \frac{|\mathcal{D}_{R}|}{|\mathcal{D}_{R}|+|\mathcal{D}_{S}|},\ 0.25,\ 0.5,\ 0.75,\ 1\)

Sweep the following parameters:

For vanilla cotraining: how do \(|\mathcal D_R|\), \(|\mathcal D_S|\), and \(\alpha\) affect the policy's success rate?

Experiment Setup

  • Train for ~2 days on a single Supercloud V100
  • Evaluate performance on 20 trials from matched initial conditions

Results

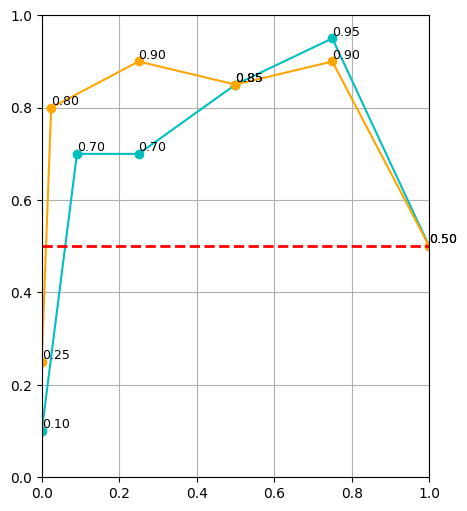
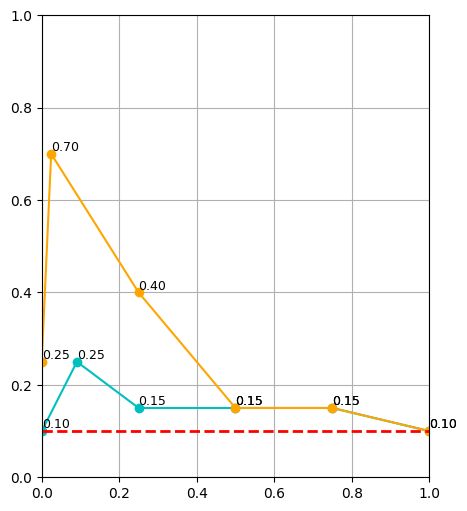
\(|\mathcal D_R| = 10\)

\(|\mathcal D_R| = 50\)

\(|\mathcal D_R| = 150\)

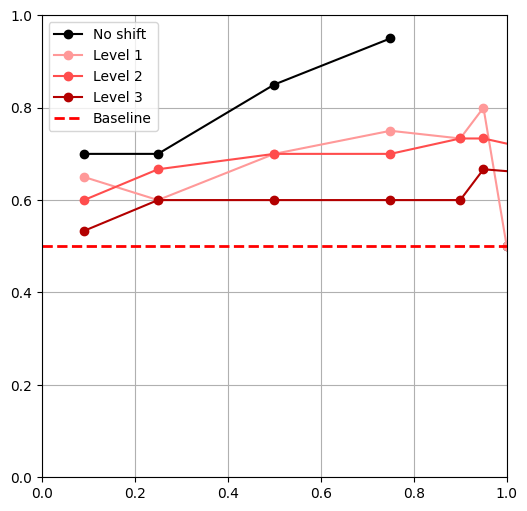
cyan: \(|\mathcal D_S| = 500\)     orange: \(|\mathcal D_S| = 2000\)     red: real only

Takeaways: \(\alpha\)

  1. Policy's are sensitive to \(\alpha\), especially when \(|\mathcal D_R|\) is small
  2. Smaller \(|\mathcal D_R|\) → smaller \(\alpha\)
  3. Larger \(|\mathcal D_R|\)  → larger \(\alpha\)
  4. If \(|\mathcal D_R|\) is sufficiently large, sim data will not help. It also isn't detrimental.

Results

\(|\mathcal D_R| = 10\)

\(|\mathcal D_R| = 50\)

\(|\mathcal D_R| = 150\)

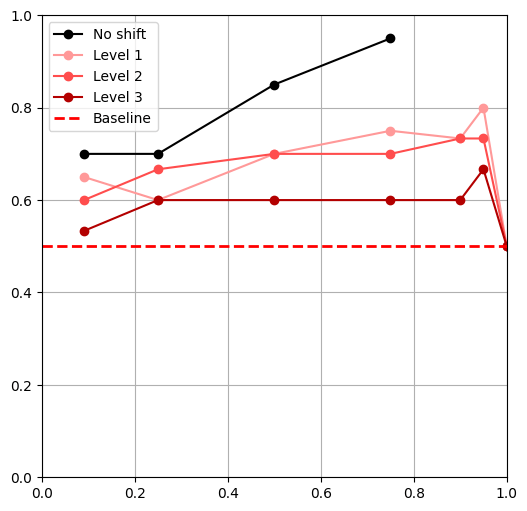
cyan: \(|\mathcal D_S| = 500\)     orange: \(|\mathcal D_S| = 2000\)     red: real only

Takeaways: \(|\mathcal D_R|\), \(|\mathcal D_S|\)

  1. Cotraining improves policy performance at all data scales
  2. Scaling \(|\mathcal D_S|\) improves performance. This effect is drastically more pronouced for small \(|\mathcal D_R|\)
  3. Scaling \(|\mathcal D_S|\) reduces sensitivity of \(\alpha\)

Initial experiments suggest that scaling up sim is a good idea!

... to be verified at larger scales with sim-sim experiments

Cotraining Theory

\mathrm{prob\ of\ error} \leq \mathrm{bound}(\alpha,|\mathcal D_R|, |\mathcal D_S|, \mathrm{dist}(\mathcal D_R,\mathcal D_S), ...)
\alpha^*(|\mathcal D_R|, |\mathcal D_S|) = \argmin_{\alpha\in[0,1]} \mathrm{bound}(\alpha, |\mathcal D_R|, |\mathcal D_S|, ...)

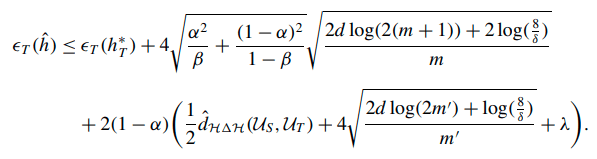
Cotraining Theory

\(|\mathcal D_R|\)

\(|\mathcal D_S|\)

\alpha^*(|\mathcal D_R|, |\mathcal D_S|) = \argmin_{\alpha\in[0,1]} \mathrm{bound}(\alpha, |\mathcal D_R|, |\mathcal D_S|, ...)

Experiments match intuition and theoretical bounds

How does cotraining help?

Sim Demos

Real Rollout

see other tab

Cotrained Policies

Cotrained policies exhibit similar characteristics to the real-world expert regardless of the mixing ratio

Real Data

  • Aligns orientation, then translation sequentially
  • Sliding contacts
  • Leverage "nook" of T

Sim Data

  • Aligns orientation and translation simultaneously
  • Sticking contacts
  • Pushes on the sides of T

How does cotraining improve performance?

Hypothesis

  1. When deployed in real, cotrained policies rely on real data and use sim data to fill in the gaps
  2. Sim data prevents overfitting and acts as a regularizor
  3. Sim data provides more information about high probability actions \(p_A(a)\)

Probably some combination of the above.

Hypothesis 1: Binary classification

When deployed in real, cotrained policies rely on real data and use sim data to fill in the gap

Policy Observation embeddings acc. Final activation acc.
50/500, alpha = 0.75 100% 74.2%
50/2000, alpha = 0.75 100% 89%
10/2000, alpha = 0.75 100% 93%
10/2000, alpha = 5e-3 100% 94%
10/500, alpha = 0.02 100% 88%

Only a small amount of real data is needed to separate the embeddings and activations

Hypothesis 1: tSNE

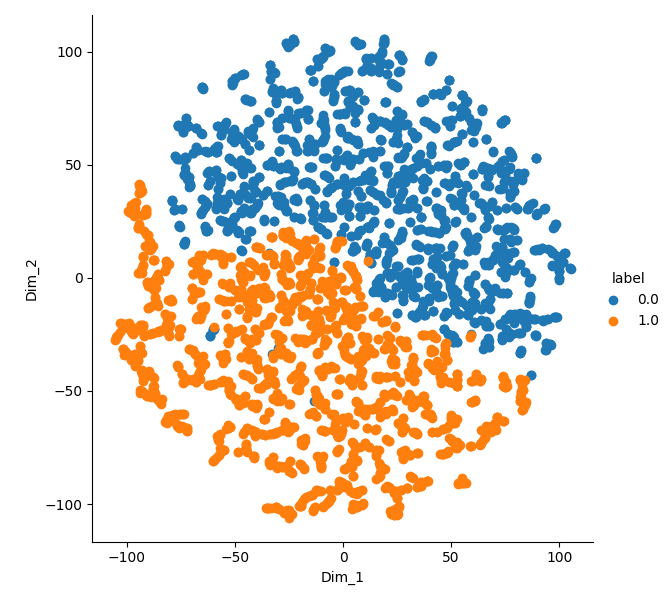
  • t-SNE visualization of the observation embeddings

Hypothesis 1: kNN on actions

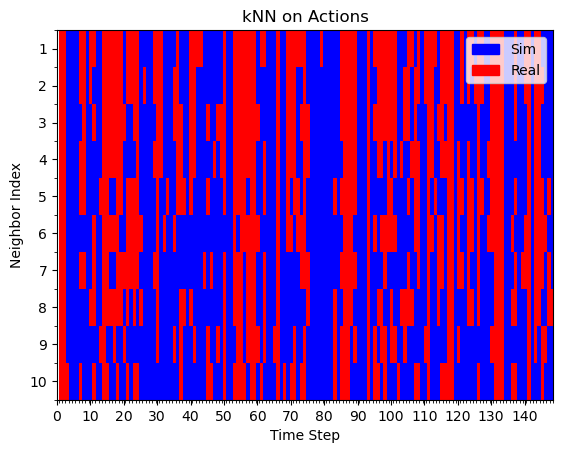
Real Rollout

Sim Rollout

Mostly red with blue interleaved

Mostly blue

Assumption: if kNN are real/sim, this behavior was learned from real/sim

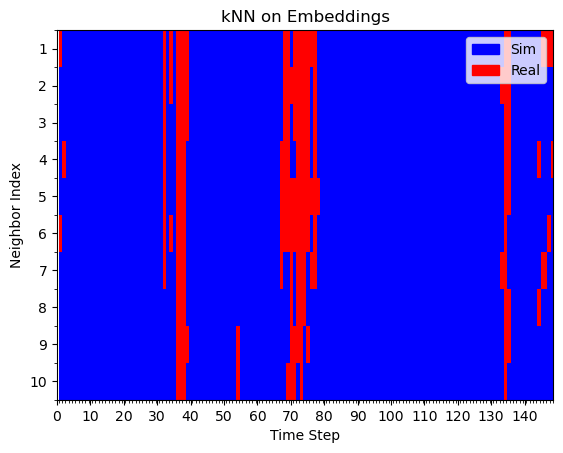
Similar results for kNN on embeddings

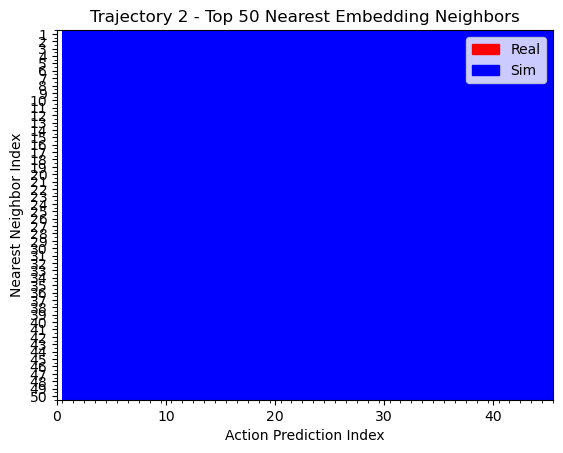
Hypothesis 1: kNN on embeddings

Real Rollout

Sim Rollout

Some red

All blue

Hypothesis 2

Sim data prevents overfitting and acts as a regularizor

\begin{aligned} \mathcal{L_{train}}=\textcolor{red}{\mathcal{L}_{objective}} + \lambda\textcolor{blue}{\mathcal{L}_{regularizer}} \end{aligned}
\mathcal L_{\mathcal D^\alpha} = \alpha \textcolor{red}{\mathcal L_{\mathcal D_R}} + (1-\alpha) \textcolor{blue}{\mathcal L_{\mathcal D_S}}

When \(|\mathcal D_R|\) is small, \(\mathcal L_{\mathcal D_R}\not\approx\mathcal L\).

\(\mathcal D_S\) helps regularize and prevent overfitting

Hypothesis 3

Sim data provides more information about \(p_A(a)\)

  • i.e. improves the cotrained policies prior on "likely actions"

Can we test/leverage this hypothesis with classifier-free guidance?

... more on this later if time allows

Hypothesis 3

Sim data provides more information about \(p_A(a)\)

Can we leverage this with classifier free guidance...

\tilde\epsilon_\theta(O, A^k,k) = (1+\omega)\epsilon_\theta(O, A^k,k) - \omega\epsilon_\theta(\emptyset, A^k,k)
\mathrm{better\ est. of\ } p_A \implies \mathrm{better\ } \epsilon_\theta(\emptyset, A^k,k)

}

Research Questions

  1. For vanilla cotraining: how do \(|\mathcal D_R|\), \(|\mathcal D_S|\), and \(\alpha\) affect the policy's success rate?
  2. How do distribution shifts affect cotraining?
  3. Propose new algorithms for cotraining
    1. Adversarial formulation
    2. Classifier-free guidance

Informs the qualities we want in sim

Distribution Shifts

Setting up a simulator for data generation is non-trivial

  • camera calibration, colors, assets, physics, tuning, data filtering, task-specifications, etc

+ Actions

What qualities matter in the simulated data?

Distribution Shifts

Distribution Shifts

Visual Shifts

  • Domain randomization
  • Color shift

Physics Shifts

  • Center of mass shift

Task Shifts

  • Goal Shift
  • Object shift

Original

Color Shift

Goal Shift

Object Shift

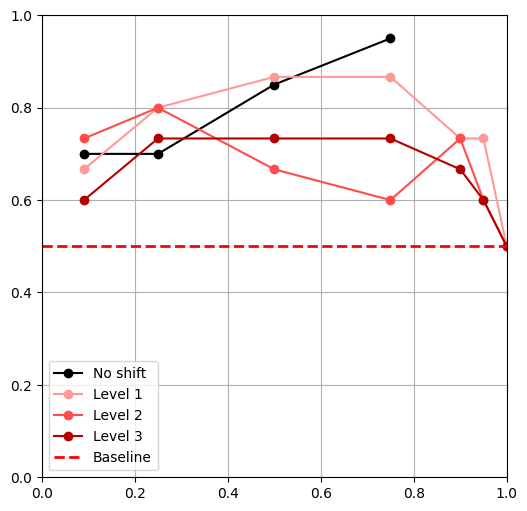
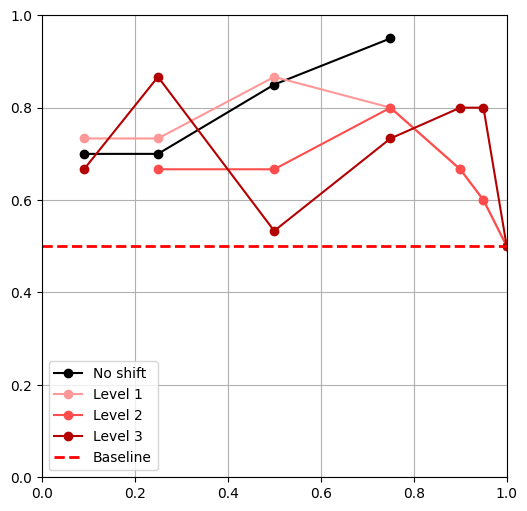
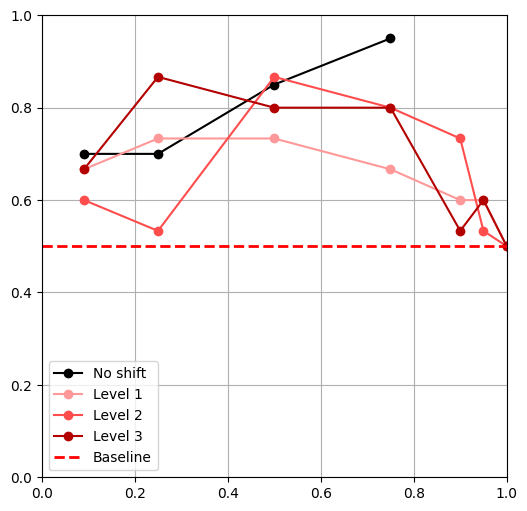
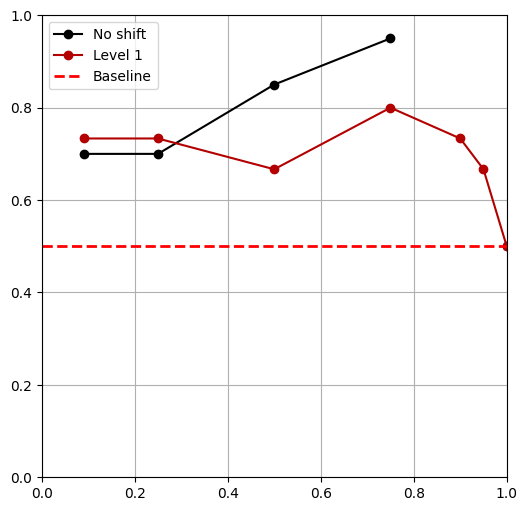
Distribution Shifts

  • Tested 3 levels of shift for each shift**
  • \(|\mathcal D_R|\) = 50, \(|\mathcal D_S|\) = 500, 
  • \(\alpha = 0,\ \frac{|\mathcal{D}_{R}|}{|\mathcal{D}_{R}|+|\mathcal{D}_{S}|},\ 0.25,\ 0.5,\ 0.75,\ 0.9,\ 0.95,\ 1\)

** Except object shift

  • All policies outperform the 'real only' baseline

Visual Shifts

Domain Randomization

Color Shift

Physics Shifts

Center of Mass Shift

Task Shifts

Goal Shift

Object Shift

Research Questions

  1. For vanilla cotraining: how do \(|\mathcal D_R|\), \(|\mathcal D_S|\), and \(\alpha\) affect the policy's success rate?
  2. How do distribution shifts affect cotraining?
  3. Propose new algorithms for cotraining
    1. Adversarial formulation
    2. Classifier-free guidance

Sim2Real Gap

Fact: cotrained models can distinguish sim & real

Thought experiment: what if sim and real were nearly indistinguishable?

Sim2Real Gap

Thought experiment: what if sim and real were nearly indistinguishable?

  1. Less sensitive to \(\alpha\)
  2. Each sim data point better approximates the true denoising objective
  3. Improved zero-shot transfer
  4. Improved cotraining bounds

Sim2Real Gap

\mathrm{prob\ of\ error} \leq \mathrm{bound}(\alpha,|\mathcal D_R|, |\mathcal D_S|, \mathrm{dist}(\mathcal D_R,\mathcal D_S), ...)

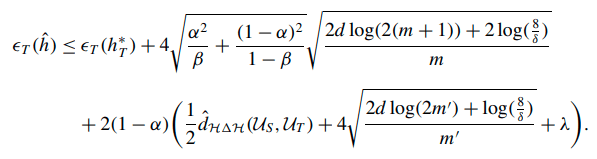
\(\mathrm{dist}(\mathcal D_R,\mathcal D_S)\) small \(\implies p^{real}_{(O,A)} \approx p^{sim}_{(O,A)} \implies p^{real}_O \approx p^{sim}_O\)

'visual sim2real gap'

Sim2Real Gap

Current approaches to sim2real: make sim and real visually indistinguishable

  • Gaussian splatting, blender renderings, real2sim, etc

\(p^{R}_O \approx p^{S}_O\)

Do we really need this? 

\(p^{R}_O \approx p^{S}_O\)

Sim2Real Gap

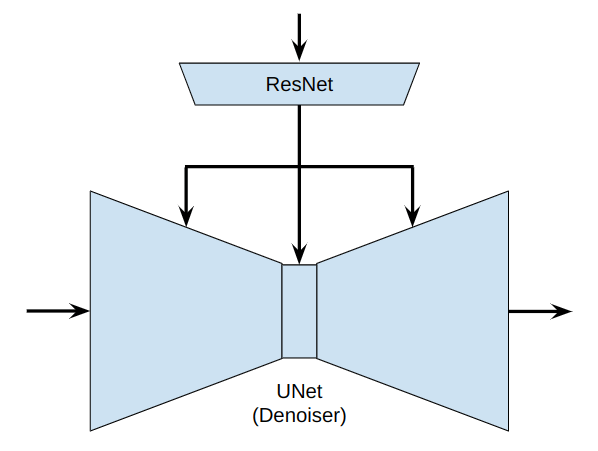
\(a^k\)

\(\hat \epsilon^k\)

\(o \sim p_O\)

\(o^{emb} = f_\psi(o)\)

\(p^{R}_O \approx p^{S}_O\)

\(p^{R}_{emb} \approx p^{S}_{emb}\)

\(\implies\)

Weaker requirement

Adversarial Objective

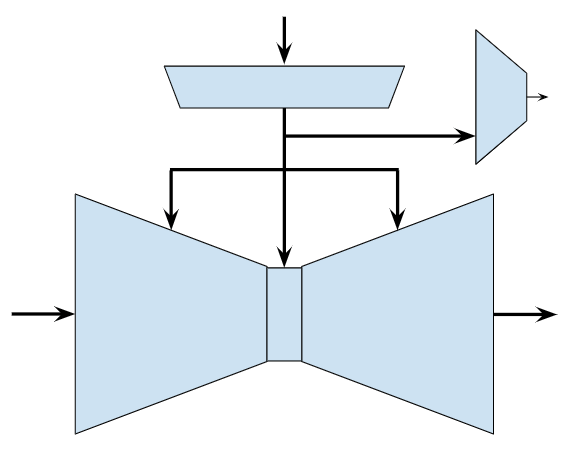
\(\epsilon_\theta\)

\(f_\psi\)

\(d_\phi\)

\(\hat{\mathbb P}(f_\psi(o)\ \mathrm{is\ sim})\)

\(\epsilon^k\)

\(a^k\)

o

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \max_\phi \mathbb E_{p^S_O}[\log d_\phi (f_\psi(o))] + \mathbb E_{p^R_O} [1-\log d_\phi (f_\psi(o))]

Adversarial Objective

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \max_\phi \mathbb E_{p^S_O}[\log d_\phi (f_\psi(o))] + \mathbb E_{p^R_O} [1-\log d_\phi (f_\psi(o))]

Denoiser Loss

Negative BCE Loss

\(\iff\)

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{JS}(p^S_{emb}, p^R_{emb})

(Variational characterization of f-divergences)

thanks Yury! :D

Adversarial Objective

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{JS}(p^S_{emb}, p^R_{emb})

Common features (sim & real)

  1. End effector position
  2. Object keypoints
  3. Contact events

Distinguishable features*

  1. Shadows, colors, textures, etc

Relavent for controls...

  • Adversarial objective discourages the embeddings from encoding distinguishable features*

* also known as protected variables in AI safety literature

Adversarial Objective

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{JS}(p^S_{emb}, p^R_{emb})

Hypothesis:

  1. Less sensitive to \(\alpha\)
  2. Less sensitive to visual distribution shifts
  3. Improved performance for \(|\mathcal D_R|\) = 10

Initial Results

\(|\mathcal D_R| = 50\), \(|\mathcal D_S| = 500\), \(\lambda = 1\), \(\alpha = 0.5\)

Performance: 9/10 trials

~log(2)

~50%

Problems...

  • A well-trained discriminator can still distinguish sim & real
    • This is an issue with the GAN training process (during training, the discriminator cannot be fully trained)
    • Image GAN models suffer similar problems

Potential solution?

  • Place the discriminator at the final activation?
  • Wasserstein GANs (WGANs)
\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{W}(p^S_{emb}, p^R_{emb})

Two Philosophies For Cotraining

1. Minimize sim2real gap

  • Pros: better bounds, more performance from each data point
  • Cons: Hard to match sim and real, adversarial formulation assumes protected variables are not relevant for control

2. Embrace the sim2real gap

  • Pros: policy can identify and adapt strongly to its target domain at runtime, do not need to match sim and real
  • Cons: Doesn't enable "superhuman" performance, potentially less data efficient

Hypothesis 3

Sim data provides more information about \(p_A(a)\)

  • Sim data provides a strong prior on "likely actions" =>improves the performance of cotrained policies

We can explicitly leverage this prior using classifier free guidance

\tilde\epsilon_\theta(O, A^k,k) = (1+\omega)\epsilon_\theta(O, A^k,k) - \omega\epsilon_\theta(\emptyset, A^k,k)

Conditional Score Estimate

Unconditional Score Estimate

Helps guide the diffusion process

\mathrm{better\ est. of\ } p_A \implies \mathrm{better\ } \epsilon_\theta(\emptyset, A^k,k)

Classifier-Free Guidance

\begin{aligned} \tilde\epsilon_\theta(O, A^k,k) &= (1+\omega)\epsilon_\theta(O, A^k,k) - \omega\epsilon_\theta(\emptyset, A^k,k)\\ &=\epsilon_\theta(O, A^k,k) + \omega(\epsilon_\theta(O, A^k,k) - \epsilon_\theta(\emptyset, A^k,k)) \end{aligned}

Conditional Score Estimate

  • Term 2 guides conditional sampling by separating the conditional and unconditional action distributions
  • In image domain, this results in higher quality conditional generation

Difference in conditional and unconditional scores

Classifier-Free Guidance

\begin{aligned} \tilde\epsilon_\theta(O, A^k,k) &= (1+\omega)\epsilon_\theta(O, A^k,k) - \omega\epsilon_\theta(\emptyset, A^k,k)\\ &=\epsilon_\theta(O, A^k,k) + \omega(\epsilon_\theta(O, A^k,k) - \epsilon_\theta(\emptyset, A^k,k)) \end{aligned}
  • Due to the difference term, classifier-free guidance embraces the differences between \(p^R_{(A|O)}\) and \(p_A\)
  • Note that \(p_A\) can be provided scalably by sim and also does not require rendering observations! 

Future Work

  1. Finish evaluating finetuned models
  2. Continue experimenting with adversarial formulations
  3. Implement and test classifier-free guidance ideas

Immediate next steps:

Future work:

  1. Sim-sim scaling laws
Made with Slides.com