machine learning
What is Machine Learning?
Everyone is talking about it.
What Is Machine Learning?
- The scientific study of algorithms and statistical models that computer systems use to perform a specific task without using explicit instructions, relying on patterns and inference instead
- Basically, programs that can solve a problem without being told how
- "Black Box," we know a solution has been found, but not exactly how it was found
When To Use Machine Learning
- A pattern exists
- We can't find that pattern mathematically
- We have or can collect enough data
Common Applications
- Autonomous Vehicles
- Spam filters
- Recommending media and products, on sites like Amazon or Netflix
- Data Mining and Data Analysis
- Setting Hotel prices
- Fault Detection in Industrial Systems
- Diagnosing tumors and other medical conditions
Problems that don't suit machine learning
- Finding if a number is prime
- Calculating digits of pi
- Finding roots to an equation
- Unable or unreasonable to collect data
Data Collection
History
- Term first coined by Arthur Samuel in 1959
- Books on machine learning for pattern recognition released in the 60s and 70s
- Gained popularity in the 80s and 90s after a reinvention of backpropagation and increase of computational power available
Types of Machine Learning Problems
- Data Mining
- Classification
- Regression
Types of learning
- Supervised Learning
- Unsupervised Learning
- Semi-supervised Learning
Components of Learning
- Input x
- Output y
- Target function: f: X -> Y
- Data
- Hypothesis
An example
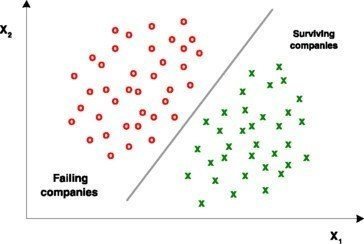
Solving A Classification Problem
steps to solving a classification problem
- Feature Generation
- Feature Selection
- Classifier Design (How to divide the feature space?)
- System Evaluation (Classification error probability, performance evaluation)
feature generation
- Features represent the objects to be classified
- Identification of features to consider for inclusion in feature space
- Features should vary widely between classes
- Done in collaboration with experts in the field of study or industry
- May involve the use of unsupervised learning to reveal correlations and patterns in the data
Feature selection
- Select the features for analysis which are most representative of the problem
- Vary widely between classes
- Rich in information
- Not duplicates or tightly correlated with another variable
Classifier Design
- How to best divide the feature space?
- Hypothesis and Experimentation
- Nature of Problem, Role of ML expert knowledge
- Occam's Razor--try the simplest and lowest-cost of the plausible solutions first
- Address problems that arise with hypothesized solution
system evaluation
- Classification error probability
- Generalizable Solution?
- If unacceptable, multiple above steps may require redesign
- Iterative development process, improvements as knowledge of problem improves
- When acceptable, ML algorithm is frozen so it no longer changes, and the "black box" is implemented.
The classification toolbox
the ml classification toolbox
- Support Vector Machines (SVM)
- k-NN "Nearest Neighbors"
- Perceptron
- Recursive Neural Network (RNNs)
- Convolutional Neural Networks (CNNs)
- Long Short-Term Memory Networks (LSTMs)
Support vector machine
- Non probabilistic linear classifier
- Divides n-dimensional feature space into classifications on either side of an n-1 dimensional hyperplane
- Relatively simple and fast
- Dataset must be linearly separable
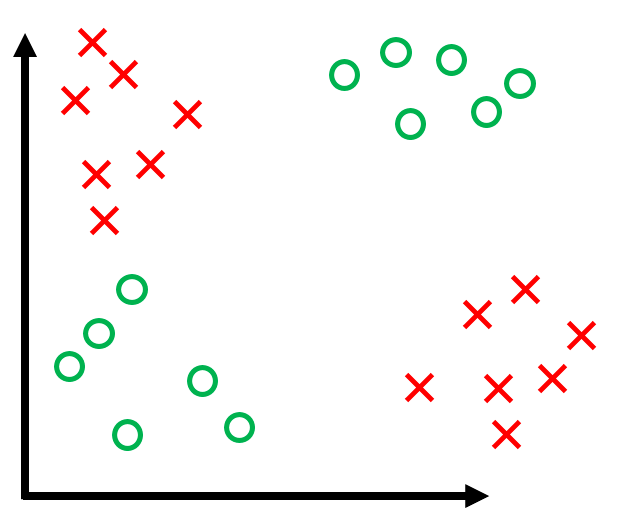
K Nearest Neighbors Classifiers
- Find K examples in training data closest in vector space to input
- Each decision is made by "majority vote"
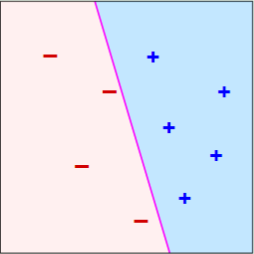
The perceptron
- Linear classifier
- Functions by assigning weights to elements of feature vectors and updating these weights.
- Input feature vectors, output classifications
- Converges if the data are linearly separable
The Perceptron
For input x
=(x_0,x_1,...,x_n)
Classify as positive (+1) if
\Sigma_{i=1}^d w_ix_i >
threshold
h(\bold{x}) = \text{sign}((\Sigma_{i=1}^d w_ix_i)-\text{threshold})
Classify as negative (-1) if
\Sigma_{i=1}^d w_ix_i <
threshold
The Perceptron Learning Algorithm
h(\bold{x}) = \text{sign}((\Sigma_{i=1}^d w_ix_i)-w_0) = \text{sign}(\bold{w}^T\bold{x})
- Pick a misclassified point
- Update the weights
- Repeat until there are no misclassified points
(\text{sign}(\bold{w}^T\bold{x_k})\ne y_k)
\bold{w}_{new}=\bold{w} + y_k\bold{x}_k
\text{Since }\bold{w}_{new}^T\bold{x}_k=\bold{w}^T\bold{x}_k+(y_k\bold{x}_k)^T\bold{x}_k \text{ and }(y_k\bold{x}_k)^T\bold{x}_k
is always of the right sign, the algorithm will always move the decision in the right direction for the point
Non-linearly separable data
The multilayer perceptron
using multiple perceptron layers to further divide the feature space
Linear separability
In this case, a single-layer perceptron converges. Additional layers are not needed. This is the base case.
non-linearly separable problem
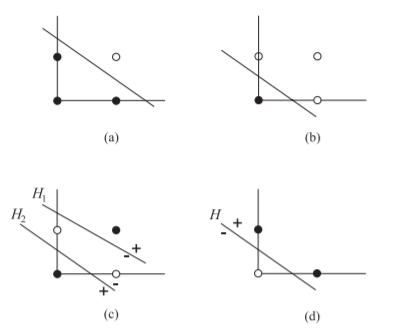
A two-layered perceptron transforms this problem into a linearly separable one. Perceptrons
H_1, H_2
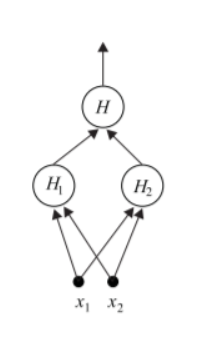
transform classification problem c) to a linearly separable case, d), which is finally solved by
H.
n = 3 case
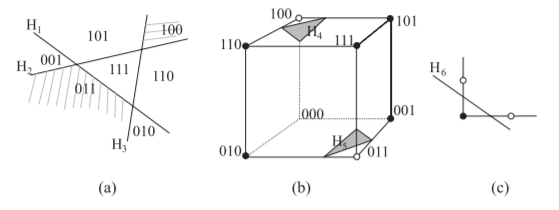
In this case, first-layer perceptrons , and transform a problem a) with three dividing planes, into a problem b), with two divisions. and then convert this problem to a linearly separable one, which is finally solved by .
H_6
H_5
H_4
H_3
H_2
H_1
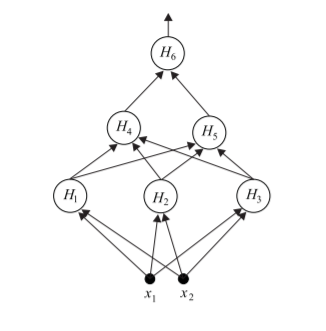
generalization to k transformations
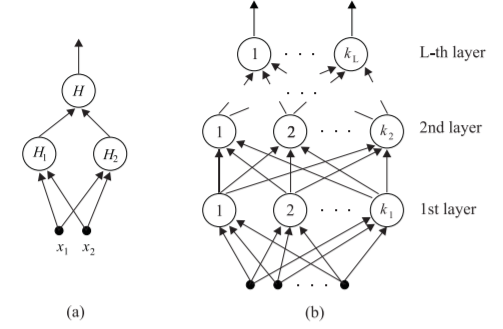
In theory, any feature space of n dimensions requiring k < n dividing hyperplanes to classify can be divided by a perceptron of k layers.
perceptron
- Feedforward Network
- In multilayer, each successive layer receives input from last
- Fully connected
Neural Networks
Biological Inspiration
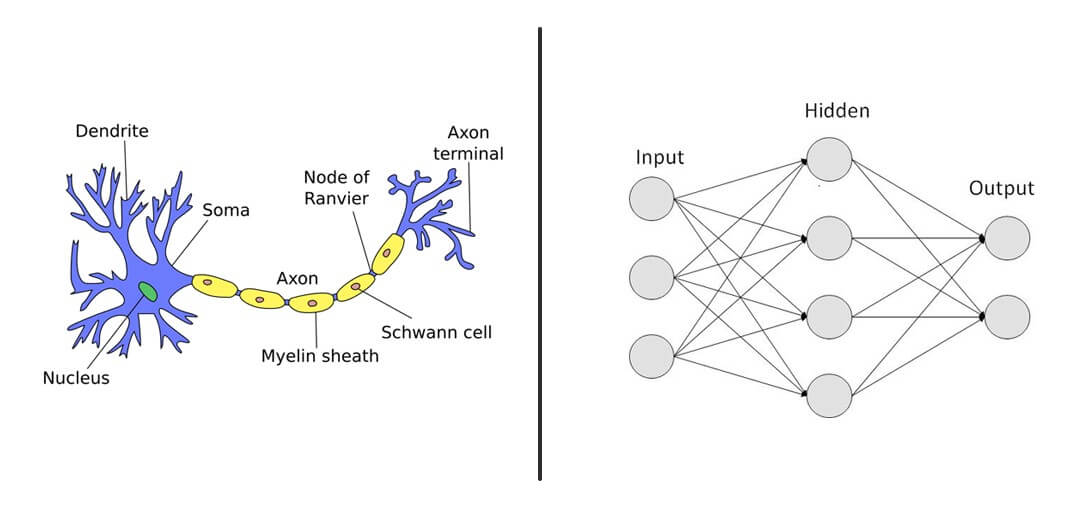
Artificial Neural Networks
- Originally created to simulate animal neural networks
- Still used for this purpose
- Adapted for many other applications
artificial neural networks
- Consists of "neurons," interconnected functions which communicate with one another
- Neurons belong to layers
- Each Neuron processes data based on an activation function
- Loosely analagous to the activation of biological neurons
Artificial neural networks
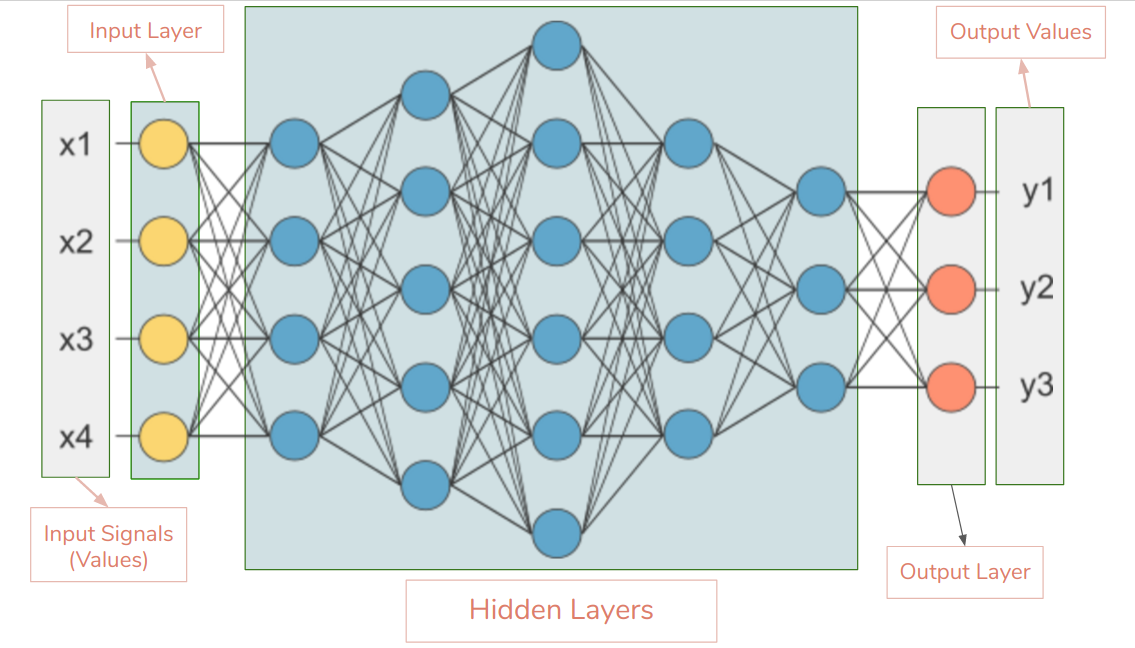
Forward Propagation
- Inputs multiplied by weight vectors to produce inputs to next layer
- Hidden layers
- Input and output layers
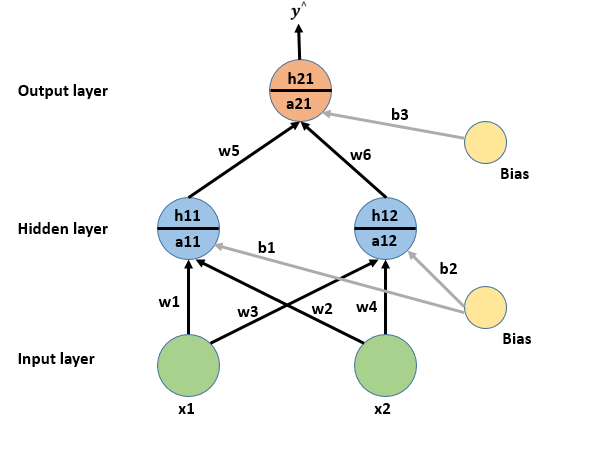
a11 = w1*x1 + w2*x2 + b1
a12 = w3*x1 + w4*x2 + b2
a21 = w5*h11 + w6*h12 + b3
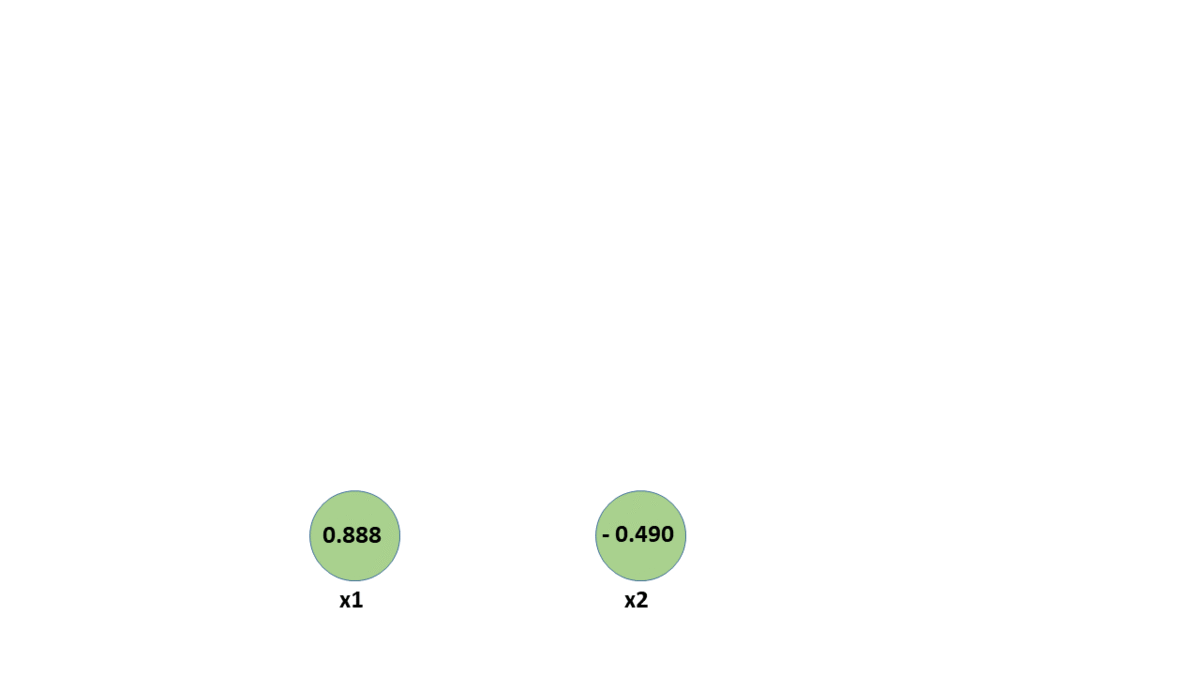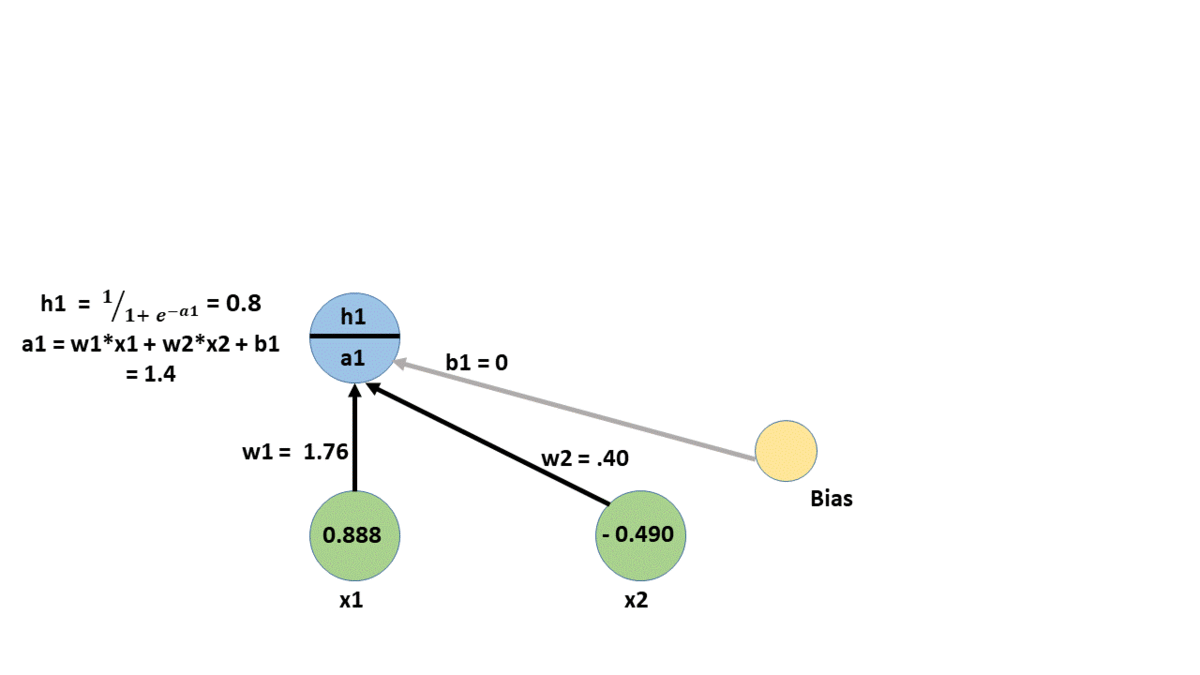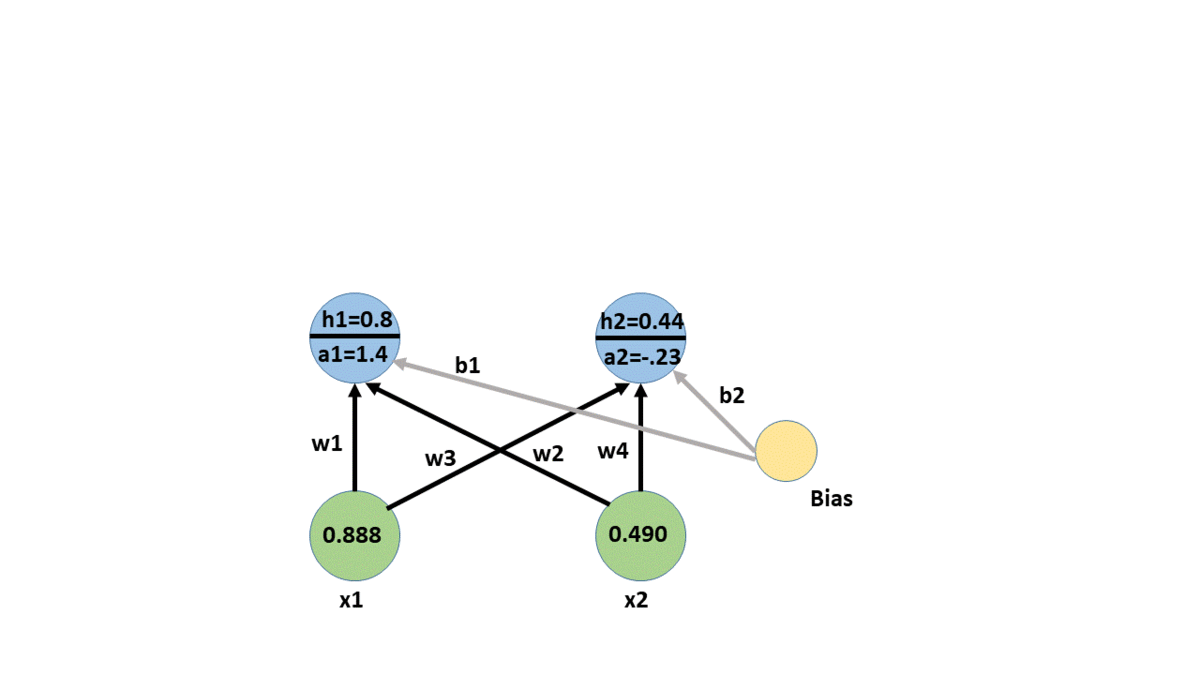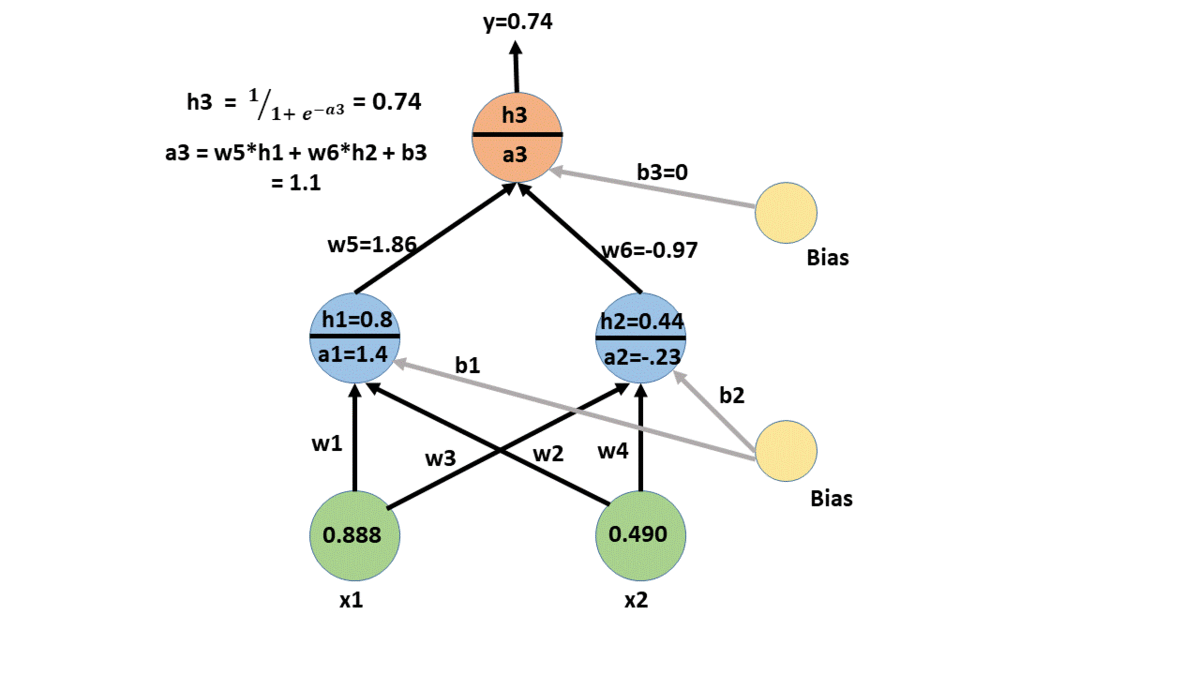
forward propagation
Back-Propagation
- After initial pass, information travels backwards through the network to correct errors
- Define a loss function to measure accuracy
- Loss function values propagate backwards through network
- Loss then minimized via Gradient Descent
Gradient descent
- Loss function takes on different values for at different weight vectors
- Take the partial derivatives of the loss function with respect to the weights
- Find the gradient vector of the loss function with respect to the weights
- Adjust weights in direction of negative gradient
- Repeat process until loss function arrives at a minimum
\bold{w}
w_i
gradient descent
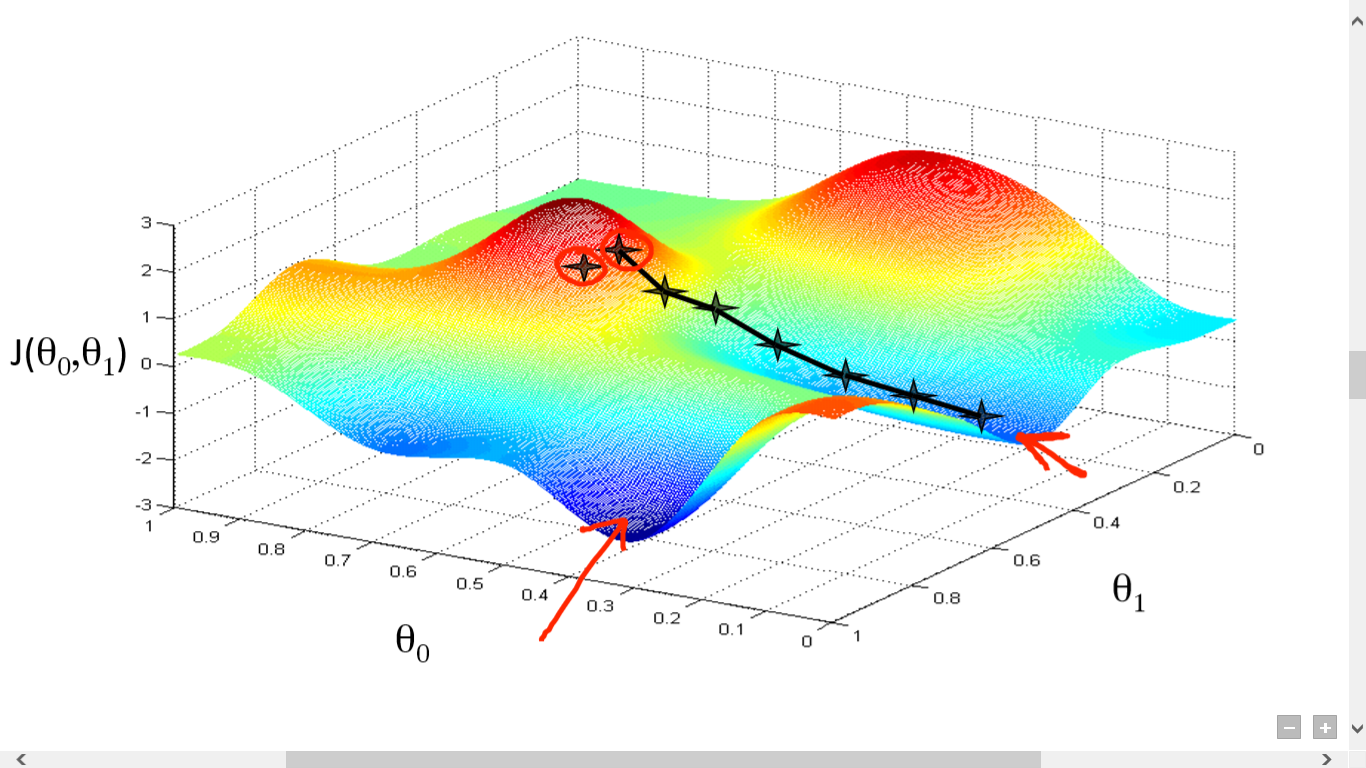
Graph of a loss function
J(\theta_0, \theta_1).
gradient descent
- There is a risk that we have only found a local minimum
- For this reason, some algorithms pursue multiple descent paths starting a set of random points
- The least of the resulting minima is chosen
- Not perfect
backpropagation example
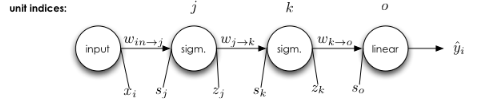
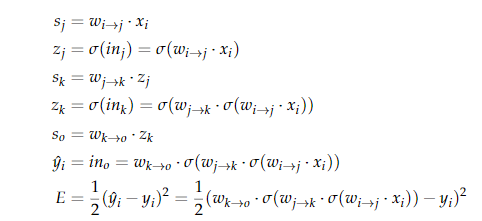
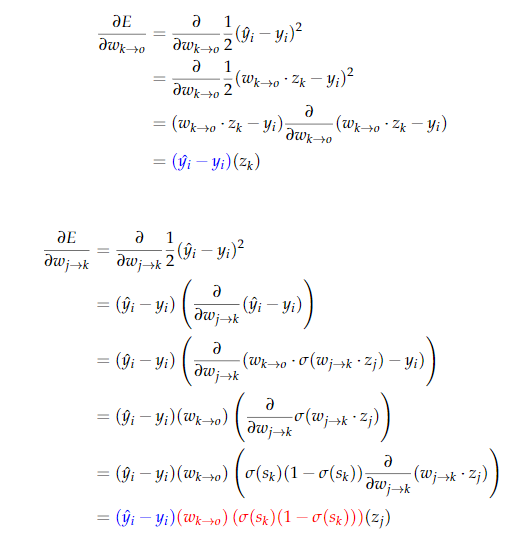
backpropagation
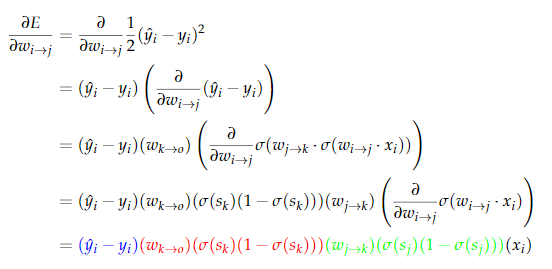
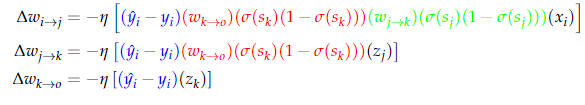
backpropagation
multiple inputs
w_{i\rightarrow k}\text{ and }w_{j\rightarrow k}
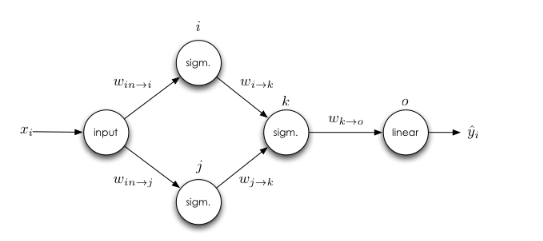
are independent, and may be derived separately
multiple outputs
w_{in\rightarrow i}
has multiple paths for backpropagation, so we sum the errors from all paths.
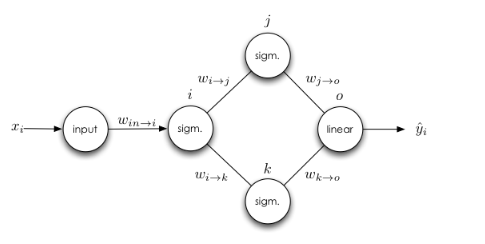
a few types of neural networks
- Convolutional Neural Networks (CNNs)
- Recurrent Neural Networks (RNNs)
- Long Short-Term Memory Networks (LSTMs)
Recurrent Neural Networks
recurrent neural networks
- RNNs feed some form of the output vector back into the network again
- This is repeated multiple times
- Weights are adjusted each time
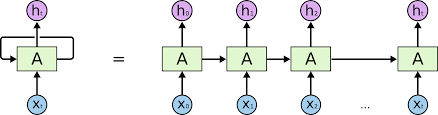
recurrent neural networks
- Used mainly for sequential data, such as time-series or language
- Sometimes important data from early recursions gets lost by the later recursions
- Small errors at the start can grow large
- Vanishing gradient
- The first problem is the reason for the LSTM
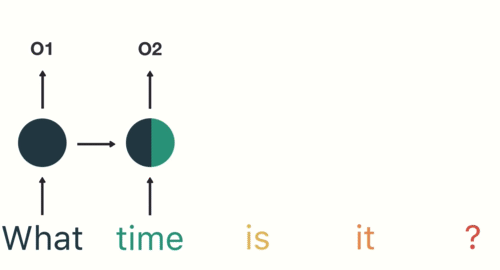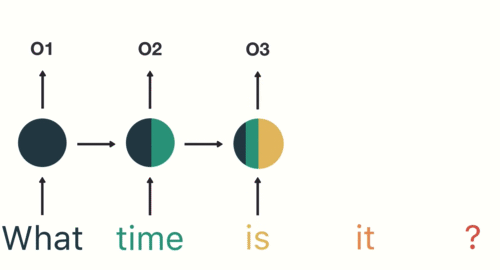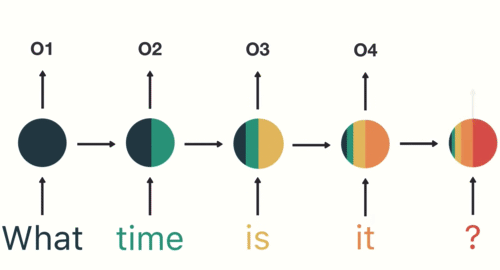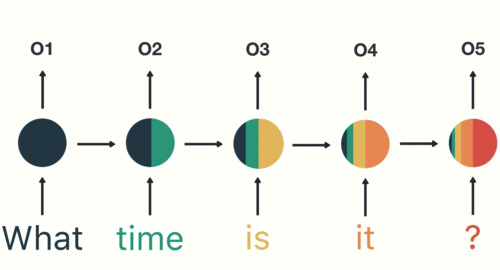
Long short term memory networks
long short term memory networks
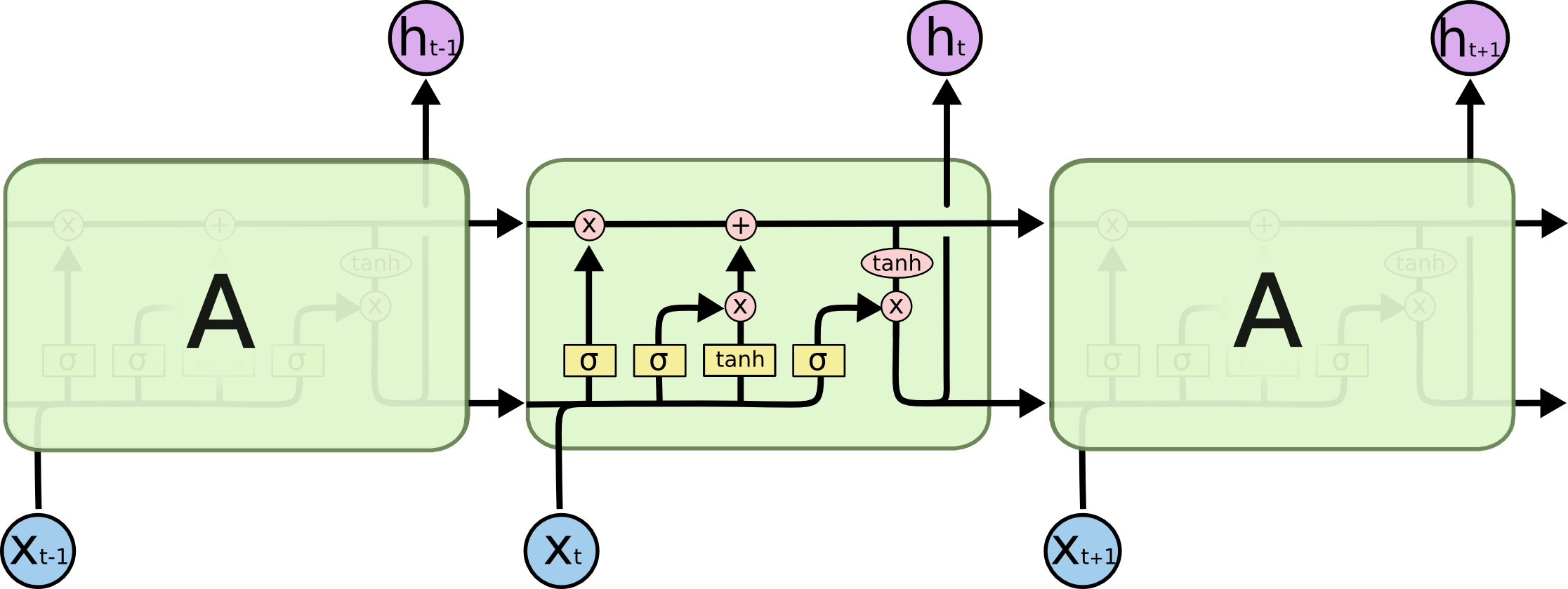
In an LSTM, each block contains a mechanism for deciding which data to keep and which to forget.
long short term memory networks
- Useful for tasks where datapoints have a time dimension
- Video analysis, text analysis, audio
Convolutional Neural Networks
convolutional neural networks
- Based on an animal visual cortex
- Uses convolutions between layers
- Feature extraction
- Image processing
convolutional neural networks
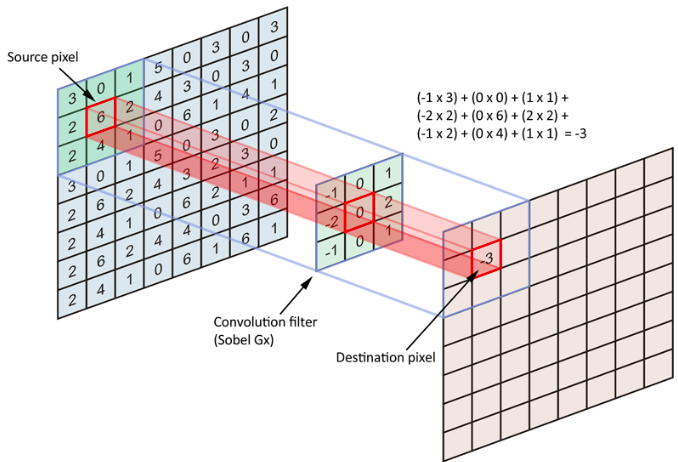
convolutional neural networks
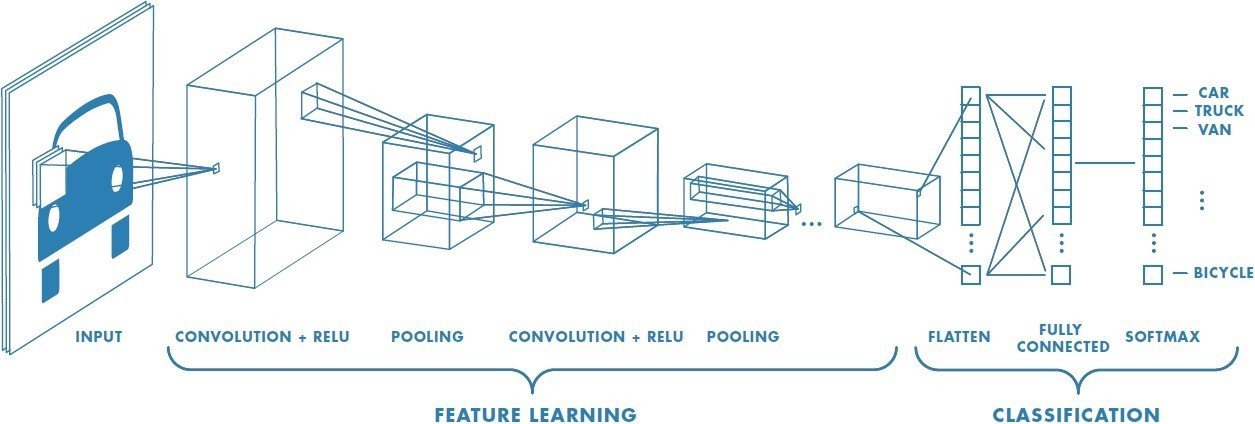
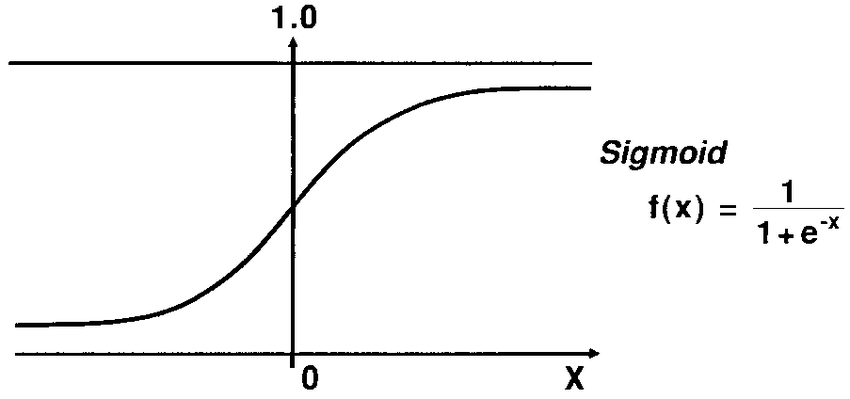
activation functions
Activation Functions
- Determine neuron outputs
- Sigmoid function:
- ReLU function:
\arctan(x)
ReLU(x) = max(0,x)
vanishing gradient
- Sigmoid activation function encounters this problem
- Recurrent Neural Networks
Relu function
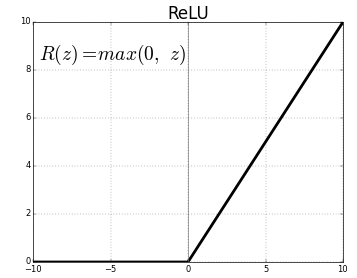
"Rectified Linear Unit"
- Dying ReLU
Other activation functions
- Leaky ReLU
- Linear
- Swish
advanced learning algorithms
active learning
- Access the desired outputs on a limited budget
- Optimize choice of inputs for which training labels are acquired
reinforcement learning
- Reinforcement uses maximization of a reward function to teach an advanced algorithm
- Used for training robots and autonomous vehicles
- Optimization and decision-making
robot learning
- Used for training robots for a variety of tasks
- Robots generate their own learning experiences
- Curriculum and Curiosity
Ethical Implications
autonomous vehicles
- Liability of firm
- Life or death decision
- Transformation of economy
Military Applications
- Autonomous weapons systems and platforms
- Strategic analysis software
- Surveillance and data collection
Privacy Concerns
- Data Collection
- Data Analysis--even metadata can reveal private knowledge
- Concerns over systems of control or evaluation
manipulation of perceptions
- Targeted Propaganda
- "Deepfakes"
- Difficulty in discerning which information is genuine
Summary
- Machine learning allows us to solve problems without explicitly finding a solution
- Classification problems
- Pattern recognition
- Data mining
- Advanced algorithms
- Transformative effect
sources
Sergios Theodoridis and Konstantinos Koutroumbas. Pattern Recognition and Neural Networks. Machine Learning and its Applications, Georgios Paliouras, Vangelis Karkaletsis, Constantine Spyropoulos, ed. pp. 169-193. Springer-Verlag, Berlin-Heidelberg, Germany. Print.
Brian Dohlansky. Artificial Neural Networks: The Mathematics of Backpropagation. 2014. Web.