Machine Learning in Intelligent Transportation

Session 2: Percepotron

Ahmad Haj Mosa

PwC Austria & Alpen Adria Universität Klagenfurt

Klagenfurt 2021

Machine Learning Tasks

1. Regression

Machine learning task are categorized by the target of the studies problems as follows:

is the problem of identifying the relationship (mathematical model) among different variables

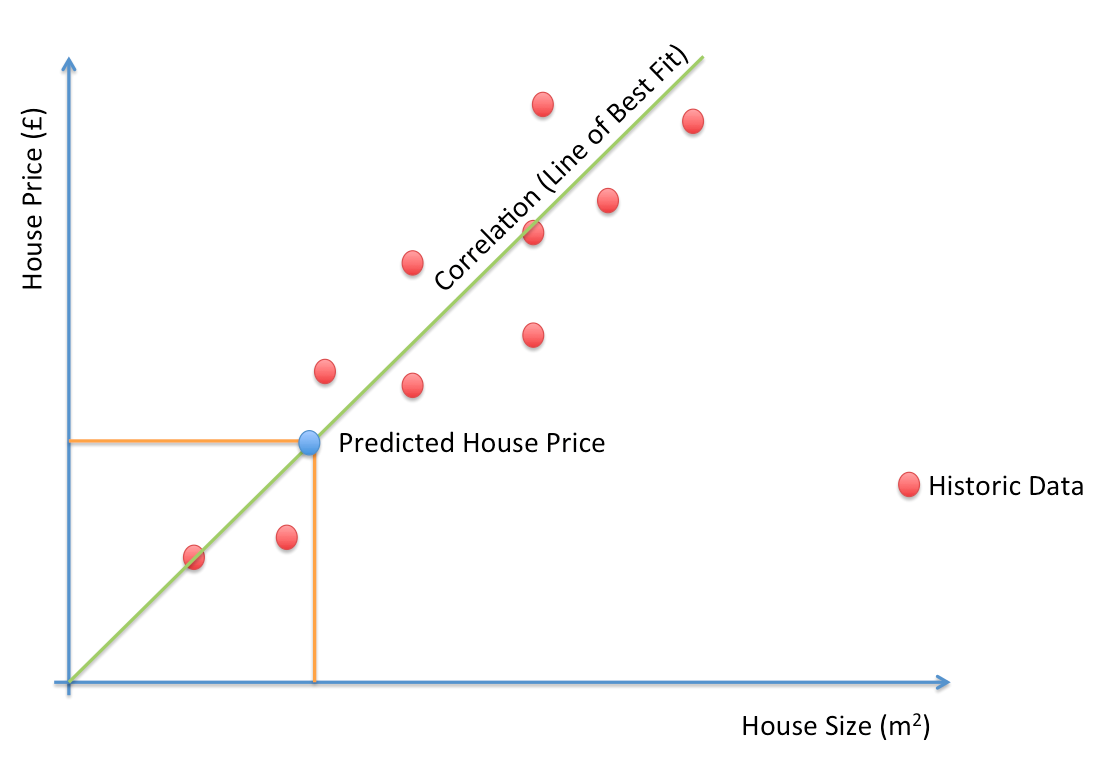
Linear Regression

A liner modeling of the relation between two or more variables

Text

y=\omega_1x+\omega_0

error

\( \omega_1 \) , \( \omega_0 \) are the weights

\( x \) is the independent variable (input/feature)

\( y \) is the dependent variable (decision/output)

Linear Regression Training

The training target of a linear regression is to find the optimum weights \( \omega_1 \) , \( \omega_0 \) that minimize the mean square error \( mse \)

Text

y=\omega_1x+\omega_0

error

p(x_0,y_0)

p(x_1,y_1)

p(x_2,y_2)

p(x_4,y_4)

p(x_5,y_5)

MSE=\frac{1}{n}\sum_{i=0}^{5}(y_i-\hat{y_{i}})^2

Gradient Descent

The training target of a linear regression is to find the optimum weights \( \omega_1 \) , \( \omega_0 \) that minimize the mean square error \( mse \)

MSE=\frac{1}{n}\sum_{i=0}^{5}(y_i-\hat{y_{i}})^2

Text

\omega

MSE

Gradient Descent

The training target of a linear regression is to find the optimum weights \( \omega_1 \) , \( \omega_0 \) that minimize the mean square error \( mse \)

J=\frac{1}{n}\sum_{i=0}^{5}(y_i-\hat{y_{i}})^2

Text

\omega

\omega_{t+1}=\omega_{t}-\rho \frac{\partial J}{\partial \omega}

\( \ \frac{\partial J}{\partial \omega} \) is the gradient

\omega_{t=0}

\omega_{t=1}

\frac{\partial J}{\partial \omega} \simeq \frac{J_{t=1}-J_{t=0}}{1}<0

\frac{\partial J}{\partial \omega} \simeq \frac{J_{t=1}-J_{t=0}}{1}>0

\( \ \rho \) is the learning rate. Large \(\rho \) large steps

Gradient Descent

The training target of a linear regression is to find the optimum weights \( \omega_1 \) , \( \omega_0 \) that minimize the mean square error \( mse \)

J=\frac{1}{n}\sum_{i=0}^{5}(y_i-\hat{y_{i}})^2

\omega_{t+1}=\omega_{t}-\rho \frac{\partial J}{\partial \omega}

\( \ \frac{\partial J}{\partial \omega} \) is the gradient

\( \ \rho \) is the learning rate. Large \(\rho \) large steps

def gradient_descent(alpha, x, y, ep=0.0001, max_iter=10000):
    converged = False
    iter = 0
    m = x.shape[0] # number of samples

    # initial theta
    w0 = np.random.random(x.shape[1])
    w1 = np.random.random(x.shape[1])

    # total error, J(theta)
    J = sum([(t0 + t1*x[i] - y[i])**2 for i in range(m)])

    # Iterate Loop
    while not converged:
        # for each training sample, compute the gradient (d/d_theta j(theta))
        grad0 = 1.0/m * sum([(w0 + w1*x[i] - y[i]) for i in range(m)]) 
        grad1 = 1.0/m * sum([(w0 + w1*x[i] - y[i])*x[i] for i in range(m)])

        # update the theta_temp
        temp0 = w0 - alpha * grad0
        temp1 = w1 - alpha * grad1
    
        # update theta
        w0 = temp0
        w1 = temp1

        # mean squared error
        e = sum( [ (w0 + w1*x[i] - y[i])**2 for i in range(m)] ) 

        if abs(J-e) <= ep:
            print 'Converged, iterations: ', iter, '!!!'
            converged = True
    
        J = e   # update error 
        iter += 1  # update iter
    
        if iter == max_iter:
            print 'Max interactions exceeded!'
            converged = True

    return w0,w1

y=\omega_1x+\omega_0

Machine Learning Tasks

1. Classification

Machine learning task are categorized by the target of the studies problems as follows:

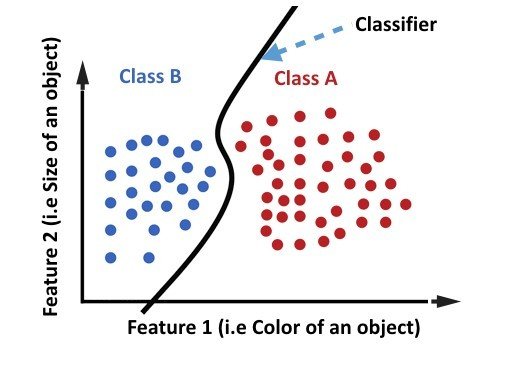
is the problem of identifying to which of a set of categories (sub-populations) a new observation

Linear Classifier

Text

x_2=\omega_1x_1+\omega_0

x_{1}

x_{2}

g(X)=W^TX

W=[\omega_1,\omega_2 ]^T

X=[x_1,x_2 ]^T

g(X)=0

g(X)>0

g(X)<0

From a linear Classifier to Neuron Models

Text

\omega^Tx

y=f(\omega,x,T)

y= { 1 \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx>TH

y= {0 \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx<=TH

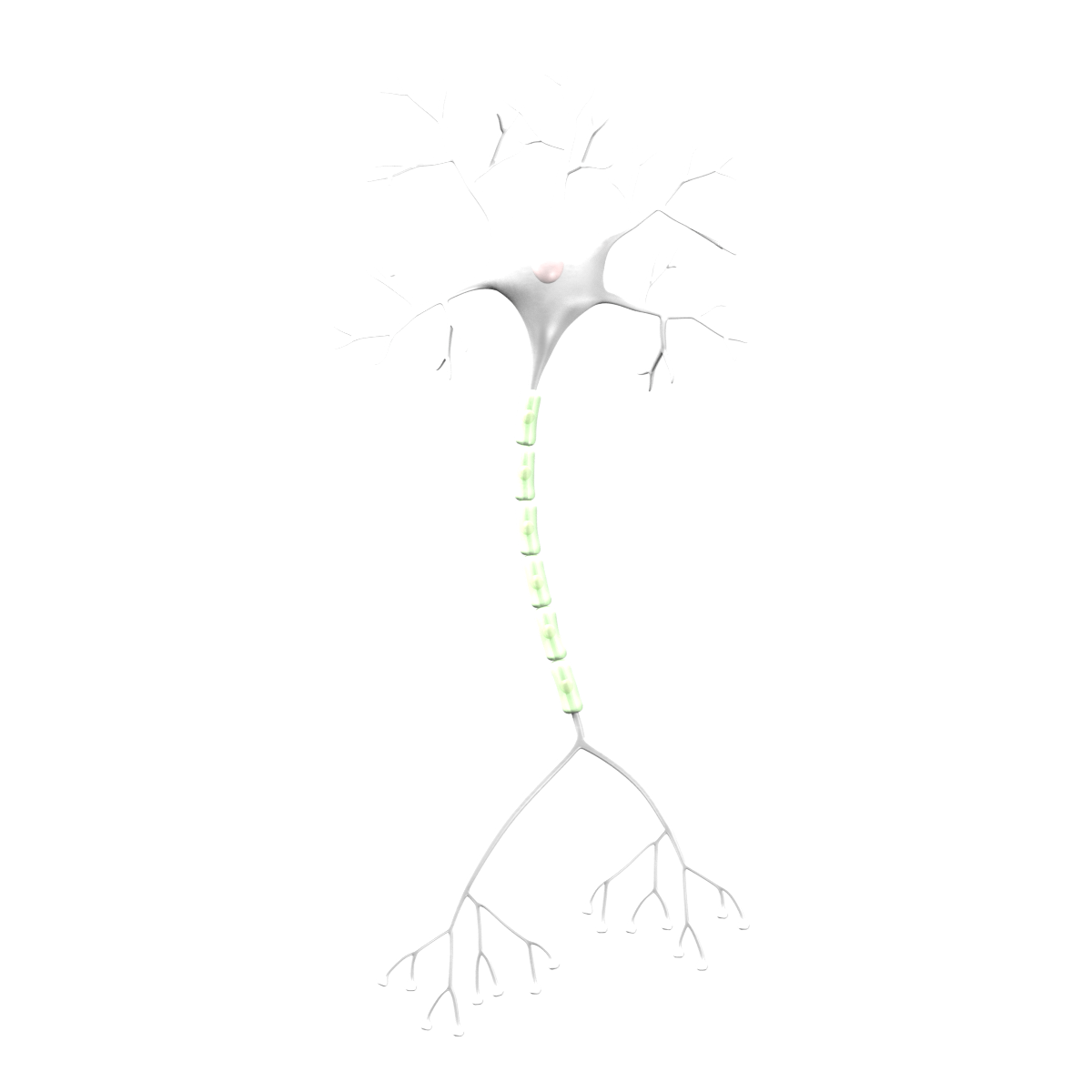
Dendrites

Axons

Cell body

\( x_1 \)

\( x_2 \)

\( y \)

Text

\( \omega= [\omega_1,\omega_2 ]^T \)

\( x=[x_1,x_2 ]^T \)

\( w_1 \)

\( w_2 \)

From a Neuron Model to Logistic Classification

Text

\omega^Tx

y=f(\omega,x,T)

y= { 1 \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx - TH >0

y= {0 \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx - TH <=0

Dendrites

Axons

Cell body

\( x_1 \)

\( x_2 \)

\( y \)

\( w_1 \)

\( w_2 \)

y= { 1 \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx - \omega_0 >0

y= {0 \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx - \omega_0 <=0

y= { 1 \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx>0

y= {0 \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx<=0

\( \omega= [\omega_1,\omega_2 ,\omega_0]^T \)

\( x=[x_1,x_2,-1 ]^T \)

Text

\( -1 \)

\( w_0 \)

The Perceptron Algorithm

The perceptron algorithm is an optimization method to compute the unknown weights \( w^T \)

Assume we have classification problem with two classes \( c_1, c_2 \)

c_1{ \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx>0

c_2{ \text{ }\text{ }\text{ if } \text{ } \text{ } \text{ } \text{ } } \omega^Tx<0

The perceptron cost is given by:

J(\omega)= \sum_{x \epsilon Y}(\delta_xw^Tx)

Where \( Y \) is the subset of the samples, which are misclassified by the classifier

\omega(t+1)=\omega(t)-\rho_t\frac{\partial J}{\partial \omega}

\frac{\partial J}{\partial \omega}=\sum_{x \epsilon Y}(\delta_xx)

\omega(t+1)=\omega(t)-\rho_t\sum_{x \epsilon Y}(\delta_xx)

The variable \( \delta_x \) is chosen so that \( \delta_x =-1 \) if \( x \epsilon c_1 \) and \( \delta_x =1 \) if \( x \epsilon c_2 \)

The Perceptron Algorithm

The perceptron algorithm is an optimization method to compute the unknown weights \( w^T \)

Choose \( \omega_0 \) randomly

Choose \( \rho_0 \)

\( t=0 \)

Repeat :

\( Y = \phi \)

For \(i=1\) to \(N\) :

If \( \delta_{x_i}\omega(t)^Tx_i \geq 0\) then \( Y=Y \cup {x_i} \)

End {For}

\( \omega(t+1) = \omega(t) - \rho \sum_{x \epsilon Y}\delta_{x} x \)

\(t=t+1\)

Until \(Y= \phi \)

J(\omega)= \sum_{x \epsilon Y}(\delta_xw^Tx)

\omega(t+1)=\omega(t)-\rho_t\sum_{x \epsilon Y}(\delta_xx)

Nonlinear Classifiers

For nonlinear separable problems a single neuron/line model in not enough

Logical OR Modeling: linear classifier?

		OR	Class
0	0	0	B
0	1	1	A
1	0	1	A
1	1	1	A

x_1

x_2

Text

x_{1}

x_2

\omega^Tx

\( y \)

\( w_2 =1 \)

Text

\( -1/2 \)

\( w_0 \)

\( w_1 =1 \)

x_{1}

x_2

\( y =x_1 +x_2 -0.5\)

Logical AND Modeling: linear classifier?

		AND	Class
0	0	0	B
0	1	0	B
1	0	0	B
1	1	1	A

x_1

x_2

Text

x_{1}

x_2

\omega^Tx

\( y \)

\( w_2 =1 \)

Text

\( -3/2 \)

\( w_0 \)

\( w_1 =1 \)

x_{1}

x_2

\( y =x_1 +x_2 -3/2\)

Logical XOR Modeling: linear classifier?

		XOR	Class
0	0	0	B
0	1	1	A
1	0	1	A
1	1	0	A

x_1

x_2

Text

x_{1}

x_2

\omega^Tx

\( y \)

\( -3/2 \)

\( 1 \)

x_{1}

x_2

\( y =(x_1 +x_2 -1/2)+2(x_1 +x_2 -3/2)- 1/2\)

Text

\( 1 \)

\( -1/2 \)

\( 2 \)

\( 1 \)

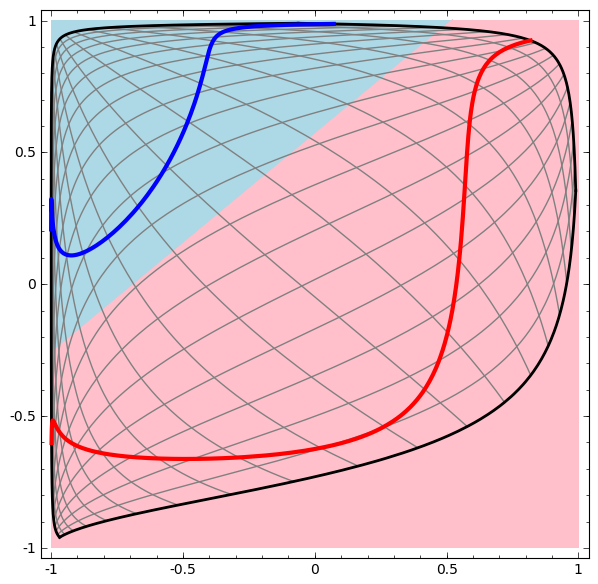
Neural Networks: topological representation

Topology is one field of mathematics that can be used to understand how neural networks work

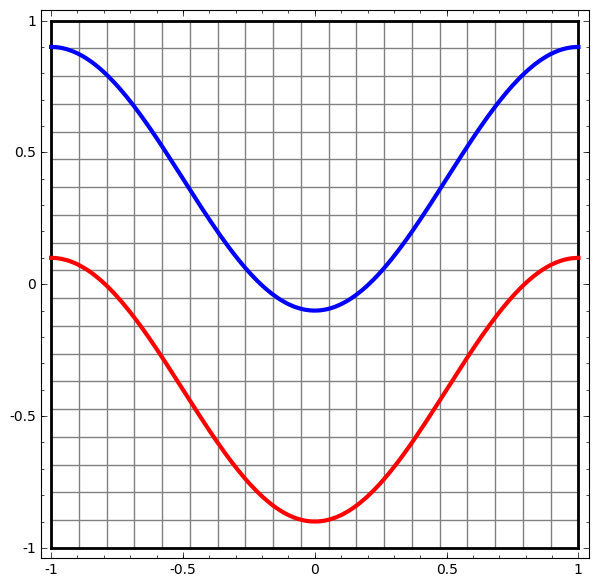
A simple NN topology example: a very simple dataset, two curves on a plane. The network will learn to classify points as belonging to one or the other.

Text

Neural Networks: topological representation

Topology is one field of mathematics that can be used to understand how neural networks work

The two regions can only be separated by a nonlinear curve

Text

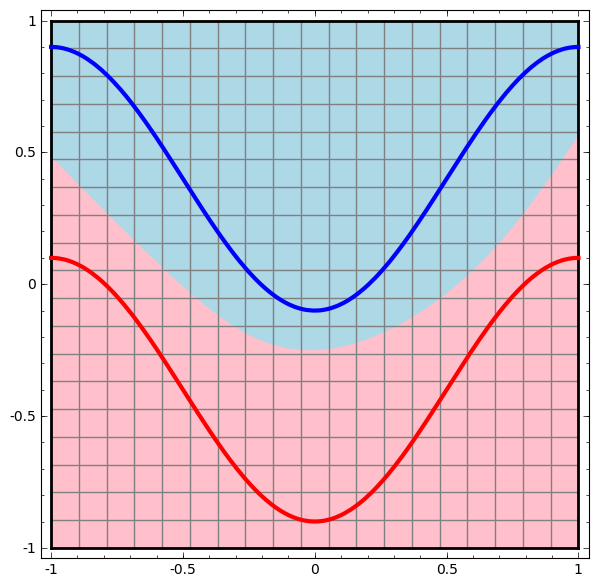
Neural Networks: topological representation

Topology is one field of mathematics that can be used to understand how neural networks work

With each layer, the network transforms the data, creating a new representation

When we get to the final representation, the network will just draw a line through the data (or, in higher dimensions, a hyperplane).