Joint Estimation and Inference for Data Integration Problems based on Multiple Multi-layered Gaussian Graphical Models

Subhabrata Majumdar & George Michailidis

Presenter: Aiying Zhang

April 25th, 2018

Content

  • Introduction
  • Statistical Model
  • Algorithm
  • Testings 
  • Performance evaluation
  • Discussion

Goal:

Build a framework based on Gaussian Graphical Model (GGM) for horizontal and vertical integration of information across multi-omics data.

 

Horizontal:  multi-conditions/subtypes

Vertical： different omics

Omics:  genomic, proteomic, metabolomic

Contribution：

Borrow information across multiple similar multi-layer networks to simultaneously perform inference on all model parameters.

 

Introduction

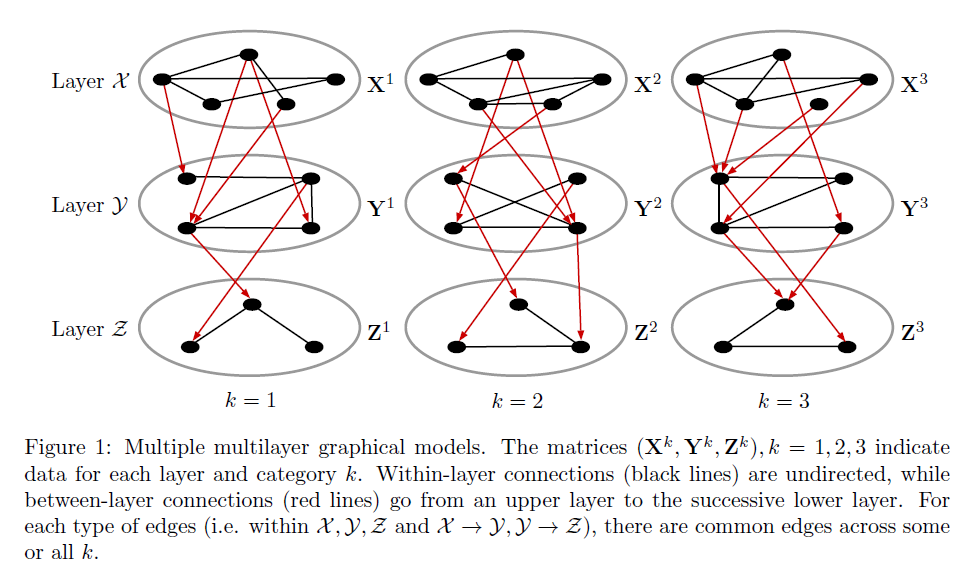
Introduction

  • Joint Multiple Multi-Layer Estimation (JMMLE)
  • Hypothesis testing in multi-layer models
  • Dataset D, K groups, M layers
  • Each layer m has pm variables(nodes) 
  • Model: for each group k=1,...,K

 

 

 

  • Parameters of interest :
    • the precision matrices
    • the coefficient matrices 

 

 

JMMLE

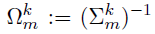
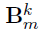
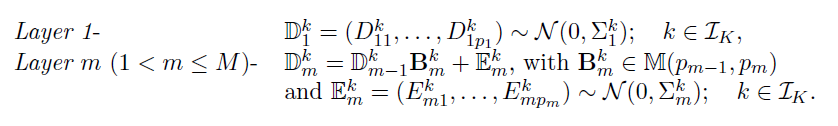
  • Special case -- a two-layer model: M=2

 

 

 

  • Goal: estimate                                from 

 

  • Focus: joint estimation of 
  • Noted:
    • For M>2, within-layer undirected edges of any m-th layer(m>1) and between-layer directed edges (m-1)-th layer can be estimated by the same method.
    • Joint estimation of                        can use other existing methods.

JMMLE

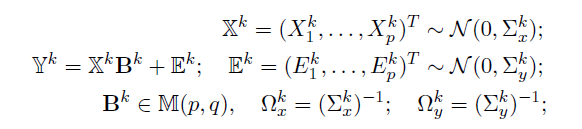
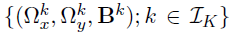
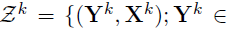
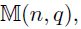
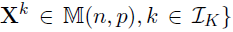
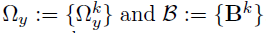
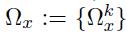
Algorithm

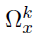
Estimation of 

  • Joint Structural Estimation Method (Ma and Michailidis, 2016)
    1. Use penalized nodewise regressions to get the graph structure
    2. Obtain neighborhood matrix
    3. Fit a graphical lasso model to obtain the sparse estimates of the precision matrix

 

 

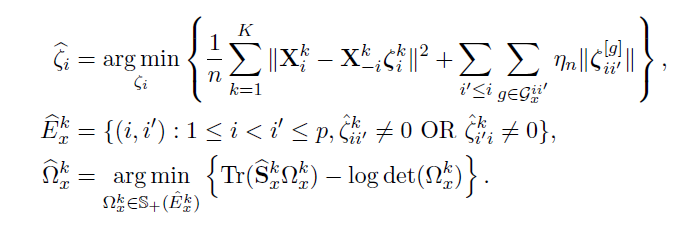
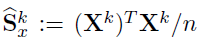
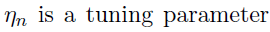
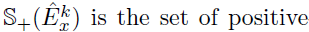
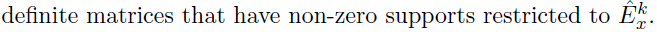
Algorithm

Joint estimation of 

​

 

 

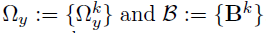
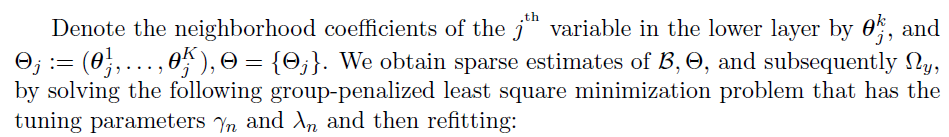
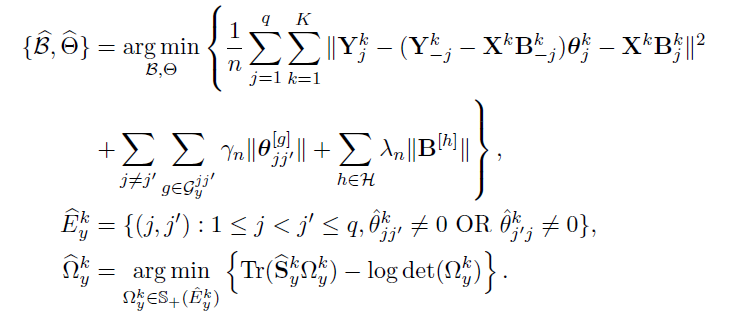
Algorithm

Alternative Block Algorithm:​

 

 

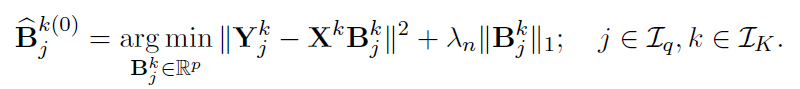
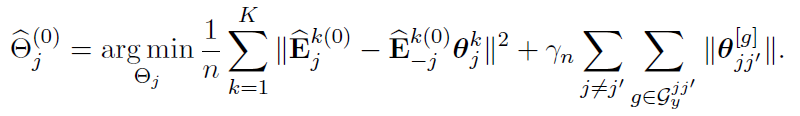
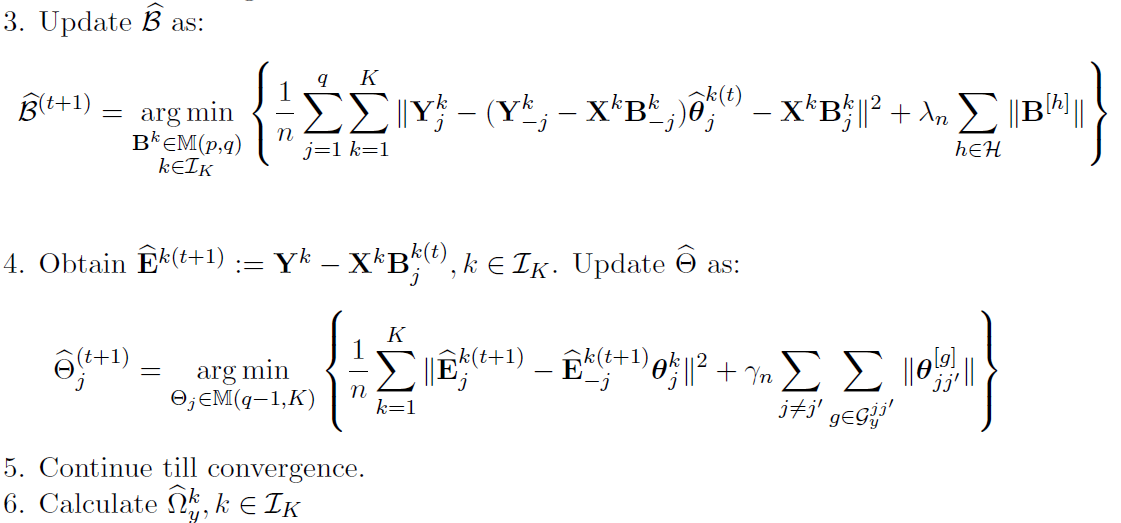
Algorithm

Tuning parameter selection:​

  • BIC (Bayesian Information Criterion) for 

 

 

 

  • HBIC (High-dimensional BIC) for 

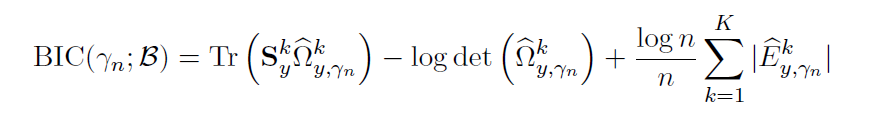
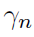
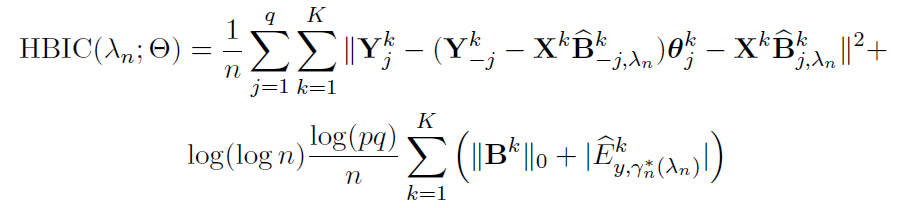
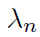
Hypothesis testing

Debiased estimator and asymptotic normality

  • Proposed by Zhang and Zhang (2014)
  • A debiasing procedure for lasso estimates for individual coeffcients in high-dimensional linear regression
  • Method:

 

 

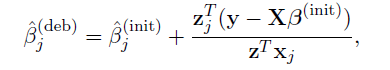
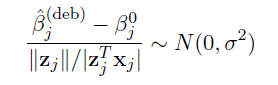
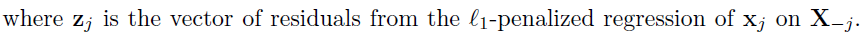
Hypothesis testing

Debiased estimator 

  • Define debiased estimates for individual rows of 

 

 

 

  • Under mild conditions, a centered and scaled 

are asymptotic normal.

 

 

(\hat{c}_i^1,...,\hat{c}_i^K)
(c^i1,...,c^iK)(\hat{c}_i^1,...,\hat{c}_i^K)

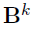
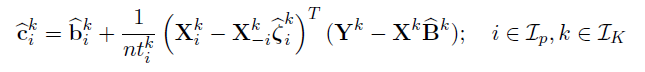
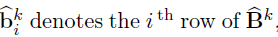
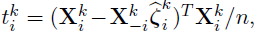
Hypothesis testing

Pairwise testing 

  • Global differences between two groups

 

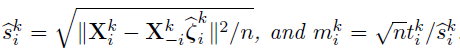
Hypothesis testing

Entrywise differences 

  • Test statistics:

 

 

  • FDR control: Benjamini-Hochberg (BH) procedure

 

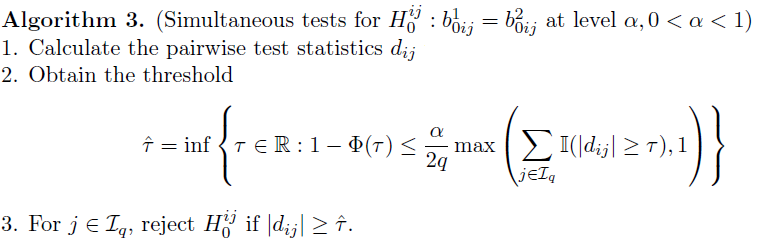
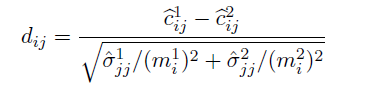
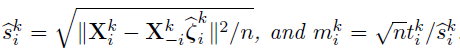
Performance

Evaluation

  • K=5, M=2

 

 

 

 

  • Within-layer: non-zero probability
  • Between-layer: non-zero probability
  • Non-zero elements independently from the uniform distribution
  • 50 replications in each setting

 

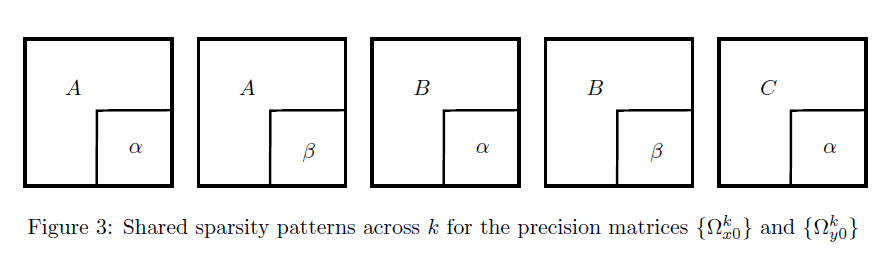
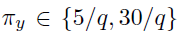
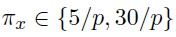
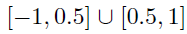
Performance

Evaluation

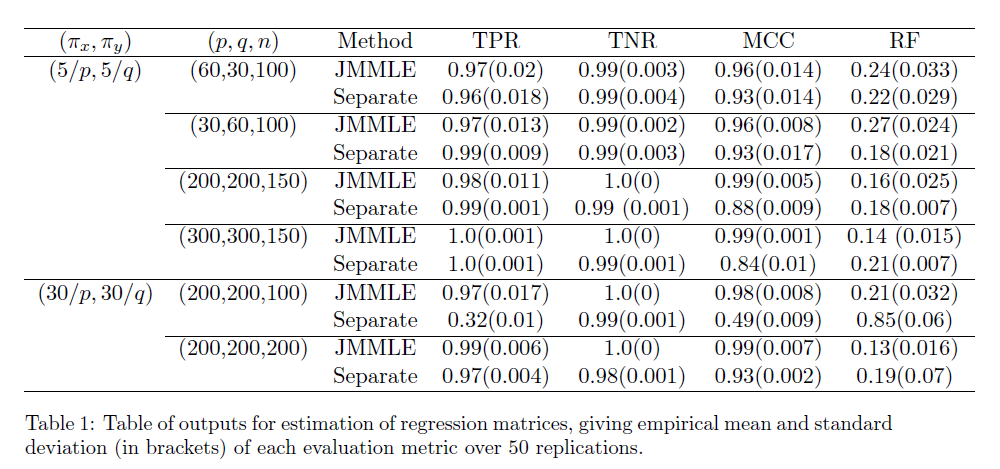
MCC: Matthews Correlation Coefficient

RF: Relative error in Frobenius norm

Performance

Evaluation

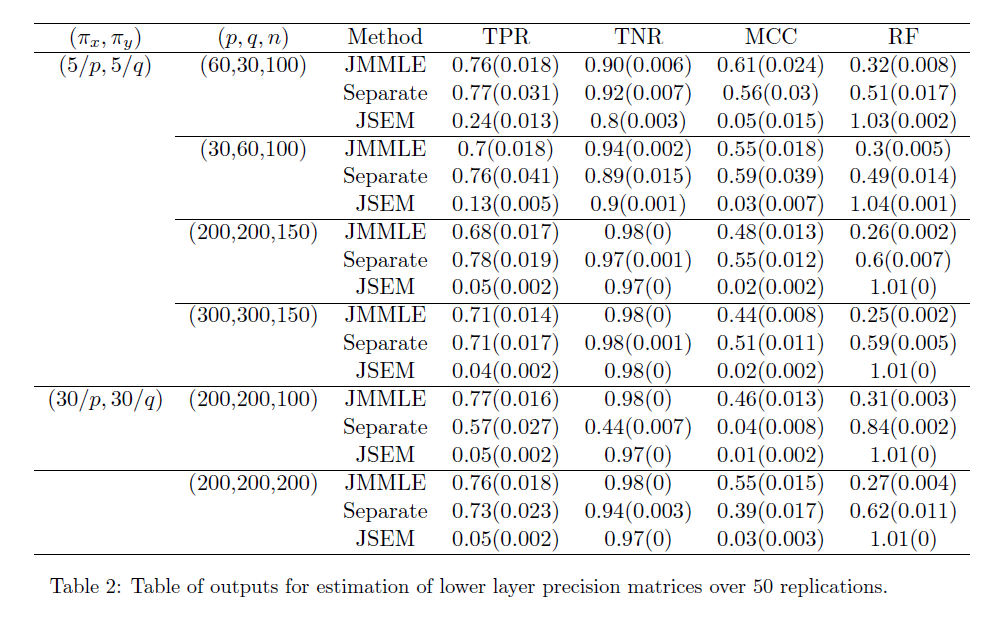
Performance

Evaluation

Simulation 2: Testing

  • K=2
  • Generate the by      randomly assigning each element to be non-zero with probability    , then drawing values of those elements from Unif{                         }.
  • Generate a matrix of differences D, where          takes values -1, 1, 0 w.p. 0.1, 0.1, 0.8, respectively.
  • Finally, set

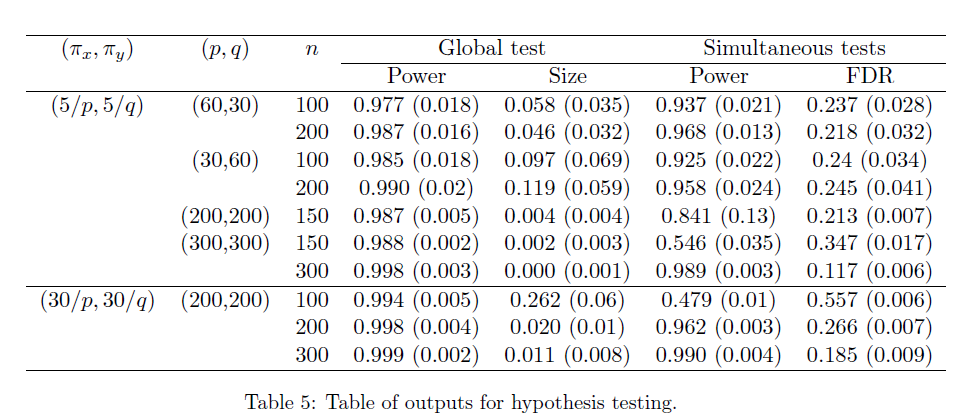
Type-1 error set                , FDR controlled at 

\pi
π\pi
(D)_{ij}
(D)ij(D)_{ij}
\alpha = 0.05
α=0.05\alpha = 0.05
\beta = 0.2
β=0.2\beta = 0.2

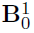
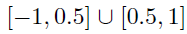
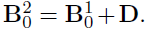
Performance

Evaluation

Discussion

​Conclusions:

  • This work introduces an integrative framework for knowledge discovery in multiple multi-layer Gaussian Graphical Models.
    • Exploit a priori known structural similarities across
      parameters of the multiple models
    • Perform global and simultaneous testing for pairwise differences

Improvements:

  • Beyond pairwise testing, need an overall test for multi-groups
  • Non-Gaussian data and graphical models with non-linear interactions 
Made with Slides.com