基礎算法

成電 - 賴冠澐，黃博崇

成功高中電子計算機研習社35th 教學

講師介紹- 賴冠澐

成功高中電子計算機研習社35th 總務/教學

講師介紹 - 黃博崇

一連串指令用以解決特定問題

aka. 解決問題的思維

演算法 algorithm

ex:最大公因數的短除法和輾轉相除法流程不一樣

升學
學完程式語言的下一步

為甚麼學演算法?

題目會給你一些輸入，而你要根據題意輸出相對應的解答
會有online judge幫你比對輸出的解答是否正確
除了解答正確以外，題目也會限制執行時間，所以要設計有效率的演算法

演算法解題

複雜度分析

code雜亂度分析??

比大小

哪個跑起來比較快結束?

(N是一個任意自然數)

int d = 0;
for(int i = 0; i < n; ++i){
	d = d + 1
}

#1

int d = 0;
for(int i = 0;i < n; ++i){
  for(int j = 0;j < n;++j){
  	d = d + 1;
  }
}

#2

	n=10	N=100	N=1000	N=10000
#1	10	100	10^3	10^4
#2	100	10000	10^6	10^8

...

只要N大了，實際運算量就差很多

第一個程式，迴圈跑N次

第二個程式，迴圈跑N次，而每一次裡面都要再跑N次

而電腦每1秒平均可以跑10^8次個運算

而要表達程式的效率，我們就需要定義程式的複雜度

時間複雜度

程式運算次數的增長趨勢
以剛剛的例子而言，#1的增長曲線為n，#2的增長曲線為n^2

Big-O Notation

作為時間複雜度的標記

若運算增長的函式為f(x)，則記為O( f(x) )

性質：

1. Big-O代表一個上界，忽略比較慢的增長函式。ex: 如果一個程式一部分的增長是n，另一部分的是n^2，則仍記為O(n^2)。

2. 如果某個數字對其增長幅度沒有引響，則不計在Big-O裡面(俗稱的常數)。ex: n, 2*n, 100*n, n+1000 增長幅度都是一樣的，為線性，所以都記為O(n)。

常數

"如果某個數字對其增長幅度沒有引響，則不計在Big-O裡面"。

忽略掉的就是所謂常數。雖然在帳面上常數不存在，但實際上是有差的，比如O(1000*n)跟O(n)就差了1000倍。

ex: 取餘數%和加法雖然都是O(1)，不過取餘數的常數比加法大了許多

空間複雜度

估算記憶體運用情形

實際可以用的記憶體也是有限的，所以空間複雜度也不能太差

性質和運算方法跟時間複雜度大同小異，把宣告過的變數加一加就可以算了

附錄：資料大小對應複雜度

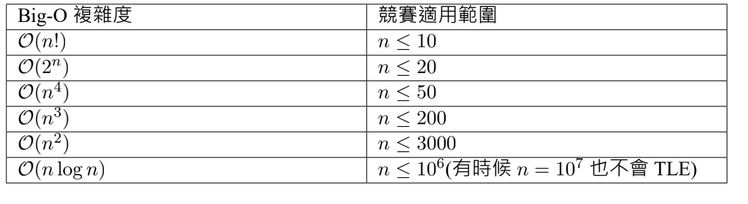
credit: ioncamp

排序

讓凌亂的數列經過排序後呈現遞增或遞減

選擇排序
泡沫排序
快速排序
合併排序

選擇排序

不停找最大值

時間複雜度O(n^2)

14

20

3

32

27

14

20

3

27

32

14

20

3

27

32

14

3

20

27

32

3

14

20

27

32

泡沫排序

讓最大值慢慢浮出來

時間複雜度O(n^2)

32

20

3

14

27

20

32

3

14

27

20

3

32

14

27

20

3

14

32

27

20

3

14

27

32

快速排序

從數列中選出一個標準

將數列依標準分成兩半

時間複雜度最好O(nlogn)

最壞O(n^2)

32

3

14

20

27

3

32

20

27

原數列

第一次分割

32

27

14

20

14

3

第二次分割

3

14

20

27

32

第三次分割

3

14

20

27

32

排序完成

合併排序

將數列不停一分為二

求出兩半以排序好的序列，再把兩半合併成另一個排序好的序列

時間複雜度O(nlogn)

32

20

3

14

27

32

20

3

14

27

32

20

3

14

27

3

14

20

27

32

14

27

3

14

20

32

20

32

3

14

27

怎麼合併(承上)

3

14

20

7

8

50

sorted:

個設定一個指針，代表目前填到哪

3

7

8

14

20

50

補充

記數排序

二分搜

終極密碼

出題者心中想一個數字，而玩家每次猜一個數字，出題者回答答案是大於還是小於玩家的猜測，直到玩家猜到答案為止。

玩家每次猜測其實就是在縮小範圍，而這就是二分搜

縮小範圍

假設目前所知答案的區間在[l, r]，每次詢問中間的數，也就是mid = (l+r)/2。

二分搜

如果大於，把目前所知區間修改為[mid, r]，因為l~mid都小於等於mid，所以可以忽略

而如果小於就變成[l, (l+r)/2]，同樣原因

複雜度：O(log n)

原因：假設原本區間有n個數，每次把區間砍半是n/2，再砍半是(n/2)/2，以此類推，直到長度剩1。

n\times 2^{-x}=1 \\ \Rightarrow 2^{-x}=n^{-1} \\ \Rightarrow -x=-\log_2 n \\ \Rightarrow x=\log_2 n

給一個已經排序好的數列，問數字k是否存在於數列裡

應用

一個一個找：O(n)，還可以更好

二分搜：每次往中間的數找，如果等於k就回傳true，而如果中間大於k，就代表在數列左半邊，小於則在右半邊。

https://algorithm-visualizer.org/branch-and-bound/binary-search

如果剛剛的數列不是排序好的，可以二分搜嗎?

單調性

因為每次取中間的值的時候，不能預測左邊一定小於中間，也不知道右邊一定大於中間，所以不能直接縮小範圍

簡言之，對一個東西二分搜(不一定是數列)，要符合單調性，也就是在連續區間上只會往同一個趨勢變化

不行

二分搜不一定要在數列上，任何有單調性的詢問也可以套用

對答案二分搜

ex；假設某問題中，如果答案是k時符合條件，而且答案是>k時也符合條件，就有單調性。(跟數列上一樣的事情)

ex：基地台

基地台

簡單作法：從小到大枚舉基地台直徑，並檢查這個直徑能不能完整

直線上有N個服務點，每架設一座基地台可以涵蓋直徑R範圍以內的服務點。

輸入服務點的座標位置以及一個正整數K，請問：在k座基地台的直徑皆相同的條件下，基地台最小直徑R為多少才能使的N個服務點皆被覆蓋到？

基地台

觀察：直徑越長，其涵蓋越多位置，也就越可能涵蓋所有服務點

換句話說：如果長度為r的直徑可以讓k個基地台覆蓋所有服務點，那直徑>r同樣可以

單調性!

二分搜：如果直徑mid可以，那就代表mid跟>mid的直徑都符合，也就是說>mid都一定不會是最小符合的直徑，所以可以把右界縮小到mid。

基地台

至於要怎麼檢查mid是否能覆蓋所有基地台，會用到後面講到的貪婪演算法

範例實作(c++)

實作方法很多，以下提供我常用的

check()函數是檢查mid這個值符合還不符合條件(ex: mid小於答案就回傳false)

int binary_search(){
  int l = 0;
  int r = n;

  while( l < r-1 ){
      int mid = ( l + r ) / 2;
      if(check(mid)){
          r = mid;
      }
      else{
          l = mid;
      }
  }

  return l;
 }
 
 
 
 
 //laialanorz

例題

二分搜尋法

雷射測試

真假子圖 - 難

掃地機器人 - 超級難，慎入

補充：三分搜

二分搜運用在一個呈現單調成長的序列上

但是如果要在呈現類似二次函數的序列上找最大(小)值呢?

目標(最小的f(x))

一樣設定一個左右界線L, R

示意：

取兩個中間值(一個中間靠右一個中間靠左)：mL, mR

怎麼縮小範圍?

考慮f(x)中，f(mL), f(mR)的大小關係

if f(mL)>f(mR)

兩種情況：

f(mL)

f(mR)

f(mL)

f(mR)

可以發現，最低點不可能出現在<ml的地方，因次可以把L=mL

怎麼縮小範圍?

if f(mL)<f(mR)

兩種情況：

f(mL)

f(mR)

f(mL)

f(mR)

最低點不可能出現在>mR的地方，因次可以把R=mR

怎麼取mL, mR?

不拘(不一定要三等分)

ex:

mR=(L+R)/2

mL=(L+mR)/2

複雜度：O(log n)

每次縮小範圍接近二分之一，所以乃為log n，但常數比二分搜大

範例實作(c++)

long double tenary_search(){
  long double l = -1e9, r = 1e9;
  while(r-l>1e-9){
      ll mr = (l + r) / 2.0;
      ll ml = (l + mr) / 2.0;
      if(check(ml) > check(mr)){
          l = ml;
      }
      else{
          r = mr;
      }
  }
  return l;
}

遞迴

函式裡面自己呼叫自己

ex: 費式數列 f(x)=f(x-1)+f(x-2)

int fib(int x){
  if(x == 1) return 1;
  else if(x == 2) return 1;
  
  return fib(x-1) + fib(x-2);
}

遞迴通常包刮：

1. 把問題拆解

2. 每個拆解後的問題處理方法都類似

輾轉相除法

公式：

gcd(a, b)=\left. \begin{cases} b, &\text{if }a=0 \\ gcd(b\%a, a) &\text{otherwise} \end{cases} \right\}

每一個小問題公式都一樣，所以用遞迴很容易

int gcd( int a, int b ){
    if(b == 0)
        return a;
    return gcd( b, a%b );
}

c++(gcc)內建公式：__gcd(a, b)

河內塔

問題拆解

觀察：如果要把最下面的盤子移動到C，那必須打C上面的盤子都先移動到B

步驟：

1.把前n-1個盤子都移動到B

2. 編號n從A移動到C

3. 前n-1個從B移動到C

問題拆解

把A, B, C想像成：起點，備胎，目標

函式：solve(移動數量，起點，備胎，目標)

操作：

solve(移動數量-1，起點，目標，備胎)

移動n到目標

solve(移動數量-1，備胎，起點，目標)

solve(3, a, b, c)

call stack

solve(2, a, c, b)

solve(1, a, b, c)

solve(1, c, a, b)

solve(2, b, a, c)

solve(1, b, c, a)

solve(1, a, b, c)

實作

void solve(int n, char a, char b, char c){
  if(n==0) return;
  solve(n-1, a, c, b);
  printf("move ring %d form %c to %c", n, a, c);
  solve(n-1, b, a, c);
}

int main(){
  int n;
  n=4;
  solve(n, 'a', 'b', 'c');
}

剪枝

當遞迴途中狀況已經不可能達成題目要求

就直接return

例題

函數運算式求值

括號匹配

子集合的和

分治

分而治之

1. 分成小問題

2. 解決小問題

3. 合併小問題

通常用遞迴實作

實例

合併排序即為分治演算法應用

不斷把數列一分為二，對排序好的兩半，可以O(n)合併為一個完整排序好的數列

複雜度

分治複雜度的數學證明：主定理 (窩不會)
每次二分，最多分到log n層 (跟二分搜一樣)
每層O(n)合併
O(n*log n)

對於一般問題，複雜度通常為：O(log n*合併複雜度)

最大連續元素和

給你一個序列，請求出最大的連續元素的和

ex: 1 2 -3 4 5，答：4+5=9

把序列切兩半，最大連續和可能出現在左邊，右邊，或橫跨左右兩邊

左右兩邊的答案都可以遞迴解決，而算橫跨的部分只需要從中間分邊往左右兩邊跑，紀錄左右兩邊過程中最大直，並加起來，

複雜度：往左右兩邊跑為O(n)，所以總共O(n logn)

例題

動態規劃

dynamic programming

複習:費式數列

f(n) = f(n - 1) + f(n - 2)

ex:直接遞迴求解f(4)

f(4)

f(3)

f(2)

f(1)

f(0)

f(1)

f(0)

總共遞迴了9次

f(2)被重複算到2次
粗估時間複雜度O(2^n)

把算過的答案存起來

f[n] = f[n - 1] + f[n - 2]

f(0)

f(1)

f(3)

f(2)

f(4)

總共計算了5次
時間複雜度為O(n)

dp的特性

大問題的最優解可從小問題最優解獲得
小問題的解不會被大問題影響
邊界答案能立刻獲得

好像跟分治好像?

主要差異：子問題會被重複利用，ex: f(x)會被f(x+1)和f(x+2)利用

dp的思路

定義問題
大問題如何從小問題求解
驗證想法正確性
然後就答對了

走樓梯

一段樓梯總共有n階

每次可以踏1階或2階

請問有幾種方法可以走到第n階?

ex:

n=1，只能走1階，方法數為1

n=2，走兩次1階，直接走2階，方法數為2

n=3，走三次1階，先1階再2階，先2階再1階，方法數為3

走樓梯

一段樓梯總共有n階

每次可以踏1階或2階

請問有幾種方法可以走到第n階?

如何定義問題?

d[i]為走到i階的方法數

d[i]如何從d[0], d[1]...d[i - 1]得到答案?

每次只能走1階或2階

假如在第i階

只有可能從第i - 1階或第i - 2階走到

走到第i階的方法數

就是走到第i - 1階+走到第i - 2階的方法數

也就是說，d[i] = d[i - 1] + d[i - 2]

結論

邊界為d[1] = 1、d[2] = 2

轉移式為d[i] = d[i - 1] + d[i - 2]

時間複雜度為O(n)

等等，是不是在哪裡看過

沒錯他就是費式數列

f(n) = f(n - 1) + f(n - 2)

表演酬勞

一名表演者總共有n個表演邀約

每天剛好有1個邀約，每個邀約有不同酬勞

但因為表演很累，這名表演者無法連續表演兩天

請問這名表演者最多能拿到多少酬勞?

ex:

n=5

酬勞為1, 2, 3, 1, 5

選擇第1, 3, 5天表演能拿到最多酬勞為9

表演酬勞

一名表演者總共有n個表演邀約

每天剛好有1個邀約，每個邀約有不同酬勞

但因為表演很累，這名表演者無法連續表演兩天

請問這名表演者最多能拿到多少酬勞?

簡化問題為在長度為n的數列a中選一些數字，而這些數字不能兩兩相鄰
如何定義問題?
定義d[i]為從a[0], a[1]...a[i]中挑選一些數字，且符合題目條件，所能得到加總的最大值
d[i]如何從d[0], d[1]...d[i - 1]求解?

在計算d[i]時，有兩種可能的情況

選擇a[i]，a[i - 1]就不能選，所以上一個選的數字只能是a[0] ~ a[i - 2]
不選a[i]，上一個選的數字只能是a[0] ~ a[i - 1]

於是d[i]只能從d[i - 2]或d[i - 1]求解

但別忘了第一種情況有選a[i]

所以d[i] = d[i - 2] + a[i]或d[i - 1]

而題目要求的是最大的酬勞

d[i] = max(d[i - 2] + a[i], d[i - 1])

結論

邊界為d[0] = a[0]、d[1] = max(a[0], a[1])

轉移式為d[i] = max(d[i - 1], d[i - 2] + a[i])

時間複雜度為O(n)

女裝

在總共n天的暑訓中

每天會從林O閎、何O甫、林O銓3人中選1人女裝

這3人在第i天女裝的美麗值分別為a[i], b[i], c[i]

但他們都不願意連續兩天女裝

請問最多的美麗值總合為多少?

ex:

n = 4

a = 1, 3, 4, 2,、b = 2, 4, 1, 5、c = 3, 1, 2, 6

第1天林O銓，第2天何O甫，第三天林O閎，第四天林O銓

能獲得最多美麗值為17

題目純屬虛構，如有雷同純屬巧合

女裝

在總共n天的暑訓中

每天會從林O閎、何O甫、林O銓3人中選1人女裝

這3人在第i天女裝的美麗值分別為a[i], b[i], c[i]

但他們都不願意連續兩天女裝

請問最多的美麗值總合為多少?

如何定義問題?

定義d[i]為0~i天最多的美麗值

那麼轉移式是d[i] = d[i - 1] + max(a[i], b[i], c[i])?

題目要求不能連續2天同1人女裝

這樣的轉移式是錯的

改變一下定義

定義d[i][j]為0~i天能獲得的最大美麗值

且第i天選擇了第j個人女裝

總共3個人，j有0, 1, 2三種狀況

假設第i天選了第0個人

第i - 1天只能選第1或2人

轉移式為

d[i][0] = max(d[i - 1][1], d[i - 1][2]) + a[i]
d[i][1] = max(d[i - 1][0], d[i - 1][2]) + b[i]
d[i][2] = max(d[i - 1][0], d[i - 1][1]) + c[i]

結論

邊界為d[0][0] = a[0]、d[0][1] = b[0]、d[0][2] = c[0]

轉移式有三條

d[i][0] = max(d[i - 1][1], d[i - 1][2]) + a[i]
d[i][1] = max(d[i - 1][0], d[i - 1][2]) + b[i]
d[i][2] = max(d[i - 1][0], d[i - 1][1]) + c[i]

時間複雜度為O(n)

拾金不昧

你居住的城市是由n * m個街區構成的矩形

為了充實口袋，咳咳，是拾金不昧

你每天都要從城市的左上角走到右下角

而你只能選擇往右或往下走

a[i][j]代表你在座標(i, j)能獲得的錢

在街區中也有一些不法之徒打算搶劫你的錢

因此a[i][j]有可能是負數

ex:

n = 3, m = 3

2 -2 3

-6 5 2

-3 7 4

最大能獲得的錢為2 + (-2) + 5 + 7 + 4 = 16

如何定義問題?

d[i][j]代表走到在座標(i, j)的最多錢

d[i][j]如何從d[0][0], dp[0][1] ...得到答案

還記得爬樓梯嗎

爬到第n步必定從第n - 1或n - 2步

跟這題一樣

每次只能往右或往下

座標(i, j)必定從(i - 1, j)或(i, j - 1)走到

d[i][j]能拿到的最多錢

就是max(d[i - 1][j], d[i][j - 1]) + a[i][j]

那邊界呢?

d[0][0] = a[0][0]

d[0][1] = max(d[-1][1], d[0][0]) + a[0][1]?

陣列的index不能放負數

那就直接無視他

d[0][1] = d[0][0] + a[0][1]

也就是說d[0][0~j] = a[0][0~j]

結論

邊界d[0][0~j] = a[0][0] + a[0][1]... + a[0][j]

d[0~i][0] = a[0][0] + a[1][0]... + a[i][0]

轉移式為d[i][j] = max(d[i - 1][j], d[i][j - 1]) + a[i][j]

時間複雜度為O(n*m)

例題

最大連續子序列

最長遞增子序列

背包問題

atcoder dp contest (dp題單，從基礎到很難都有)

貪婪

每次都做最好決定的演算法

aka.只有一個轉移點的動態規劃

要如何判斷直徑mid是否覆蓋所有服務點?(基地台可以任意擺)

基地台

1. 排序服務點座標

2. 如果目前基地台直徑超過mid，就換下一個基地台(並且基地台數量+1)

3. 看用到的基地台數量是不是<=k

每次把基地台撐到最極限一定是最好的

給n線段[Li, Ri]，問最多可以剩下幾個使得所有線段不相交

經典題 -線段相交

性質：當從左到右擺放線段的時候，如果兩個線段重疊，總是取右端點最小的線段一定最好

證明：右端點越大的話則會佔據越多之後能擺放的位置

根據這性質，作法就是：對線段右界排序，然後從左到右，如果線段的左界覆蓋左邊的線就拋棄

經典題 -線段相交

貪婪

1. 找出一個固定走法

2. 證明其永遠不會比較差

例題

誰先晚餐

物品堆疊

蘿莉切割問題(霍夫曼編碼)

昨天晚上，一等一被殺了

STL函式庫

標準樣板函式庫

c++內建函式庫，集結非常多好用資料結構和演算法實作

只要#include <bits/stdc++.h> 就會引入所有STL工具

函式設計為可以互相混用，讓運用非常有彈性，宣告方法也大致類似

常用STL函式

vector

動態陣列(= c的malloc，可以隨時擴展陣列容量) 的實作，並可配合許多其他STL函式操作

宣告：vector<TYPE> NAME(SIZE, INIT);

尾端新增：NAME.push_back(VALUE);

隨機存取：NAME[INDEX]

大小：NAME.size()

sort

O(nlogn)排序

小到大：

sort(起點，終點);

大到小：

sort(起點，終點，greater<TYPE>());

如果用vector：起點=NAME.begin()，終點=NAME.end()

一般陣列：起點=NAME，終點=NAME+長度

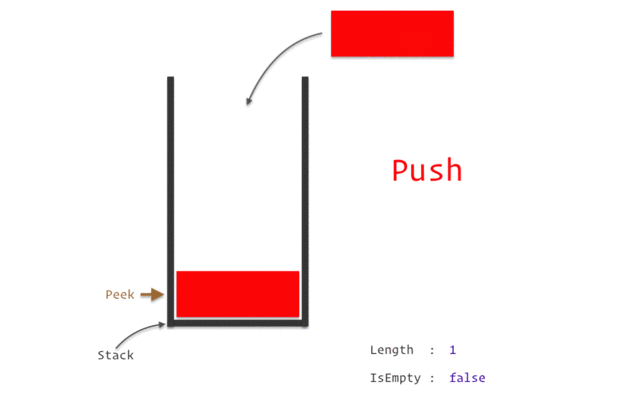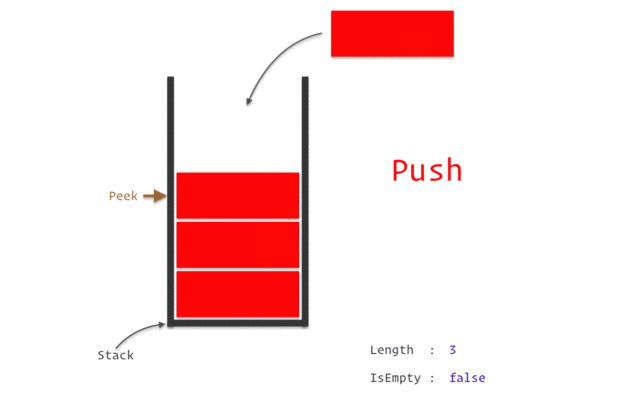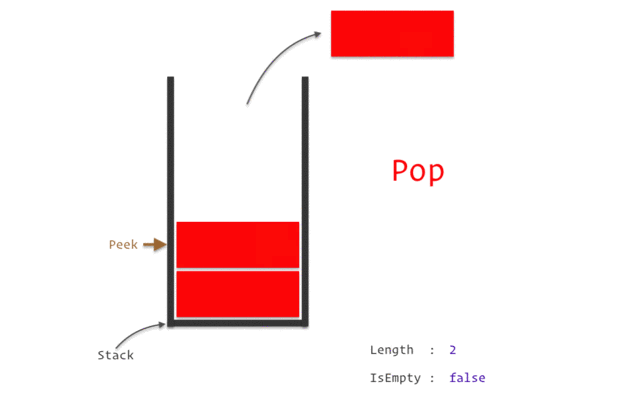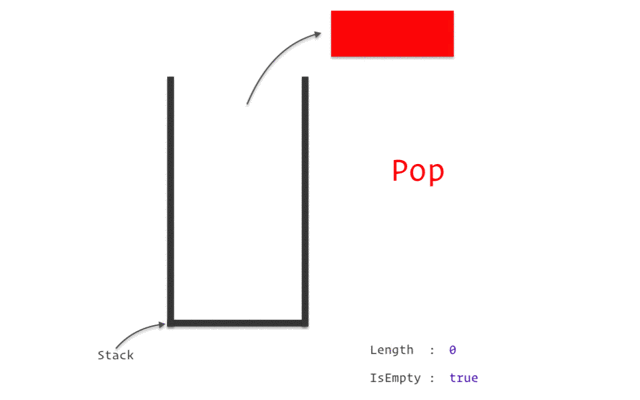
stack

stack資料結構實作

stack性質：先進後出(如圖)

宣告：stack<TYPE> NAME;

新增：NAME.push(VALUE);

刪除：NAME.pop();

頂端直：NAME.top()

大小：NAME.size()

基本上用vector是一樣的事

queue

像排隊一樣

先進先出

宣告：queue<TYPE> NAME;

新增：NAME.push(VALUE);

刪除：NAME.pop();

前端值：NAME.front()

尾端值：NAME.back()

大小：NAME.size()

priority_queue

優先度最高的會在頂端，heap實作

刪除，新增：O(log n)

取值：O(1)

宣告：priority_queue<TYPE> NAME;(值最大在頂端)

priority_queue<TYPE,vector<int>,greater<int>> NAME(最小)

新增：NAME.push(VALUE);

刪除：NAME.pop();

頂端值：NAME.top()

大小：NAME.size()

set

自動排序且不重複的集合，紅黑樹(平衡二元樹)實作
複雜度皆為log n

宣告：set<TYPE>NAME;

新增：NAME.insert(VALUE);

刪除：NAME.erase(VALUE);

找第一個大於等於：NAME.lower_bound(VALUE)

大小：NAME.size()

map

由一個關鍵字和對應的值組成

複雜度皆為log n

宣告：map<TYPE,TYPE>NAME;

新增：NAME.insert({VALUE,VALUE});

刪除：NAME.erase(VALUE);

找第一個大於等於：NAME.lower_bound(VALUE)

大小：NAME.size()

lower_bound / upper_bound

對陣列二分搜的實作

lower_bound：找出陣列中"大於或等於"val的最小值的位置

auto it = lower_bound(v.begin(), v.end(), val);

upper_bound：找出vector中"大於"val的最小值的位置：

auto it = upper_bound(v.begin(), v.end(), val);

基礎算法

成電 - 賴冠澐，黃博崇

講師介紹- 賴冠澐

講師介紹 - 黃博崇

目錄

演算法 algorithm

為甚麼學演算法?

演算法解題

複雜度分析

code雜亂度分析??

比大小

時間複雜度

Big-O Notation

常數

空間複雜度

附錄：資料大小對應複雜度

排序

怎麼合併(承上)

二分搜

縮小範圍

二分搜

應用

單調性

對答案二分搜

基地台

基地台

基地台

範例實作(c++)

例題

掃地機器人 - 超級難，慎入

補充：三分搜

怎麼縮小範圍?

怎麼縮小範圍?

範例實作(c++)

遞迴

輾轉相除法

河內塔

問題拆解

問題拆解

實作

剪枝

例題

分治

實例

複雜度

最大連續元素和

例題

動態規劃

貪婪

基地台

經典題 -線段相交

經典題 -線段相交

貪婪

例題

昨天晚上，一等一被殺了

STL函式庫

標準樣板函式庫

vector

sort

stack

queue

priority_queue

set

map

lower_bound / upper_bound

參考資料