Optimization-based Motion Planning for Legged Robots


Alexander W. Winkler
May 14, 2018 \( \cdot \) PhD Defense
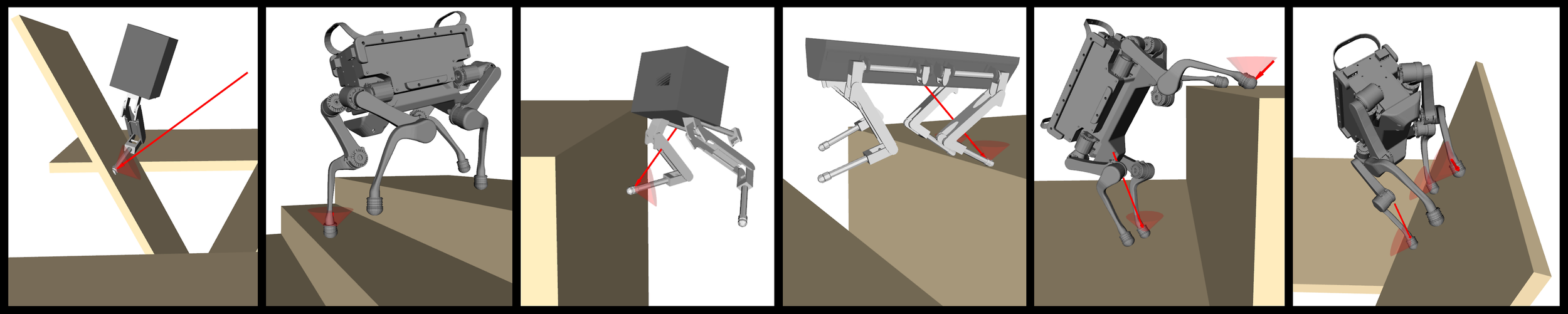
Why legged machines?
\( \bullet \) traverse rubble in earthquake \( \bullet \) reach trapped humans \( \bullet \) climb stairs \( \bullet \)...
Agility ...vs rolling
Strength ...vs flying
\( \bullet \) carry heavy payload \( \bullet \) open heavy doors \( \bullet \) rescue humans \( \bullet \) ...
vs

Source:
ANYbotics, Anymal bear, "Image: https://www.anybotics.com/anymal", 2018; Boston Dynamics, Atlas, "Image: https://www.bostondynamics.com/atlas", 2016; Italian Institute of Technology, HyQ2Max "Image: https://dls.iit.it/robots/hyq2max, 2018; Alphabet Waymo, Firefly car, "Image: https://waymo.com", 2016, DJI, Phantom 2 drone, "Image: https://www.dji.com/phantom-2", 2016
Source: https://www.youtube.com/watch?v=NX7QNWEGcNIa
Source: https://www.youtube.com/watch?v=arCOVKxGy9E


Goal \( \cdot \) position \( \cdot \) velocity \( \cdot \) duration \( \cdot \)
Robot \( \cdot \) kinematic \( \cdot \) dynamic
Environment \( \cdot \) terrain \( \cdot \) friction \( \cdot \) ...
Outline
Desired Motion-Plan
Actuator Commands
force \( \cdot \) torque
Tracking
Controller
off-the-shelf
NLP Solver
Mathematical Optimization Problem
Direct Methods
e.g. Collocation
?
Paper I
"Fast Trajectory Optimization for legged Systems using Vertex-based ZMP Constraints"
Paper 2
"Gait and Trajectory Optimization for Legged Systems through Phase-based End-Effector Parameterization"




Task



Generating dynamic motions
Dynamic Model
Linear Inverted Pendulum


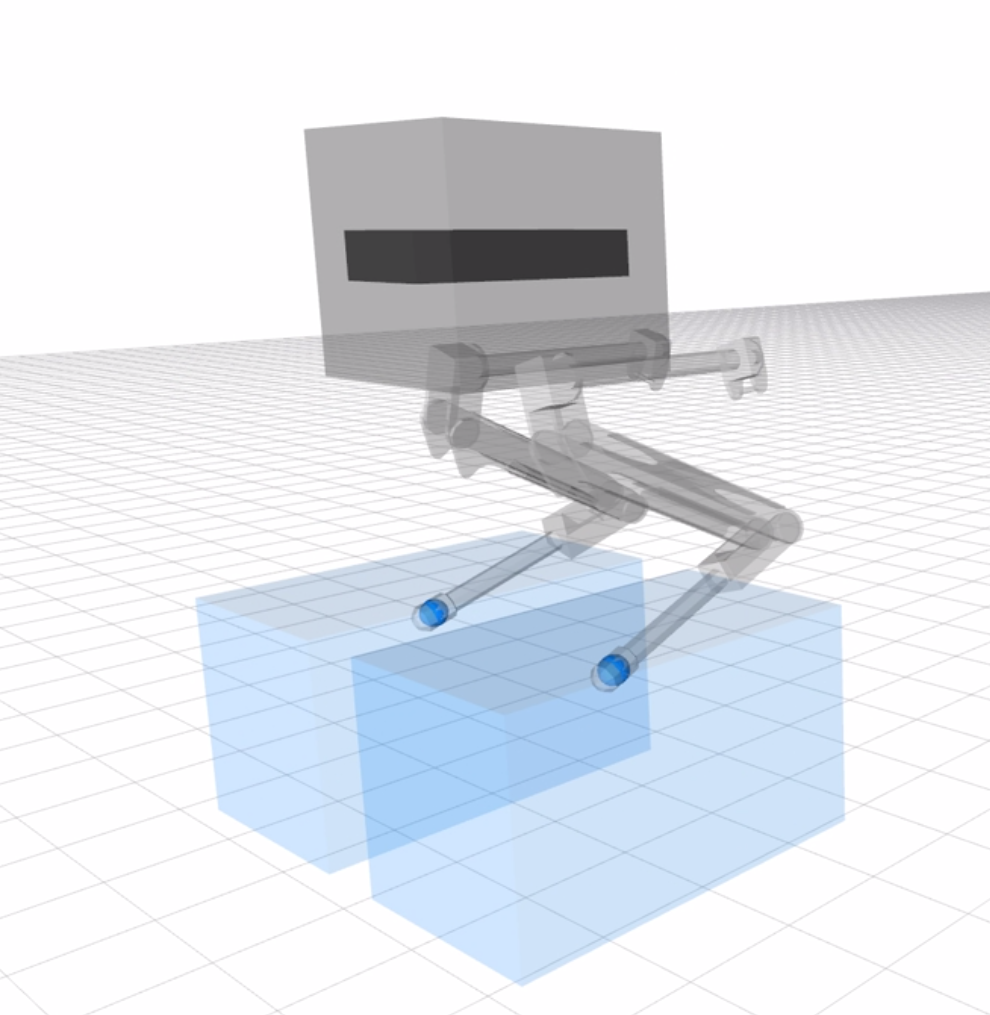
Unilateral Contact Forces \(\Leftrightarrow\) CoP inside Support-Area
Difficult for single point-contacts or lines


Ordering of contact points

Vertex-Based Zmp-Constraint Formulation

Fast Trajectory Optimization for Legged Robots using Vertex-based ZMP Constraints
IEEE Robotic and Automation Letters (RA-L) \( \cdot \) 2017
A. W. Winkler, F. Farshidian, D. Pardo, M. Neunert, J. Buchli






foothold
change
Simultaneous Foothold and CoM Optimization
Fast Trajectory Optimization for Legged Robots using Vertex-based ZMP Constraints
IEEE Robotic and Automation Letters (RA-L) \( \cdot \) 2017
A. W. Winkler, F. Farshidian, D. Pardo, M. Neunert, J. Buchli




- Contact schedule
- CoM height (no jumps)
- Body orientation (horizontal)
- Foothold height (flat ground)
Mathematical Optimization Problem
predefined:
Motion-Plan Search Space
restrict search space



all motion-plans \( \{ \mathbf{x}(t), \mathbf{u}(t) \} \)



fullfills all contraints

Gait and Trajectory Optimization for Legged Systems through Phase-based End-Effector Parameterization
IEEE Robotic and Automation Letters (RA-L) \( \cdot \) 2018
A. W. Winkler, D. Bellicoso, M. Hutter, J. Buchli
Towards integrated motion-planning

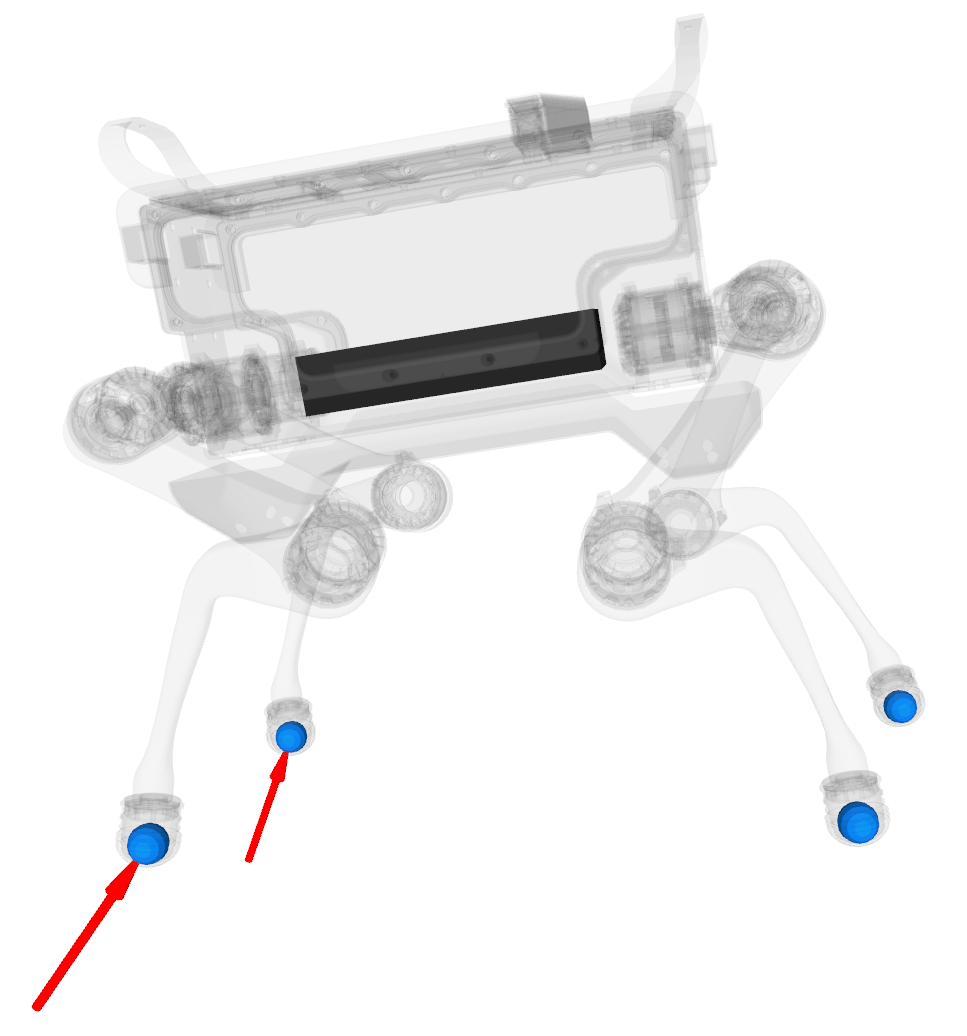
Dynamic Model
Single Rigid Body \( \cdot \) Newton-Euler Equations


Kinematic Model
Range-of-Motion Box \(\approx\) Joint limits

Gait Optimization
R | 2 | L | R | 2
R | 0 | R | 2 | R | 2
.... gait defined by continuous phase-durations \(\Delta T_i\)

without Integer Programming
Gait and Trajectory Optimization for Legged Systems through Phase-based End-Effector Parameterization
IEEE Robotic and Automation Letters (RA-L) \( \cdot \) 2018
A. W. Winkler, D. Bellicoso, M. Hutter, J. Buchli
Sequence:

swing
stance
individual foot always alternates between and

Phase-Based End-Effector Parameterization
Know if polynomial belongs to swing or stance phase
-
Foot \( \mathbf{p}_i(t)\) cannot move while

Physical Restrictions
- Forces \(\mathbf{f}_i(t)\) cannot exist while


standing
swinging

Terrain constraints
Foot can only stand on terrain
Forces can only push
Forces inside friction pyramid
- height map \( h(x,y) \in \mathbb{R}\)
- normals \( \mathbf{n}(x,y) \in \mathbb{R}^3 \)
- tangents \( \mathbf{t}(x,y) \in \mathbb{R}^3 \)
Given:



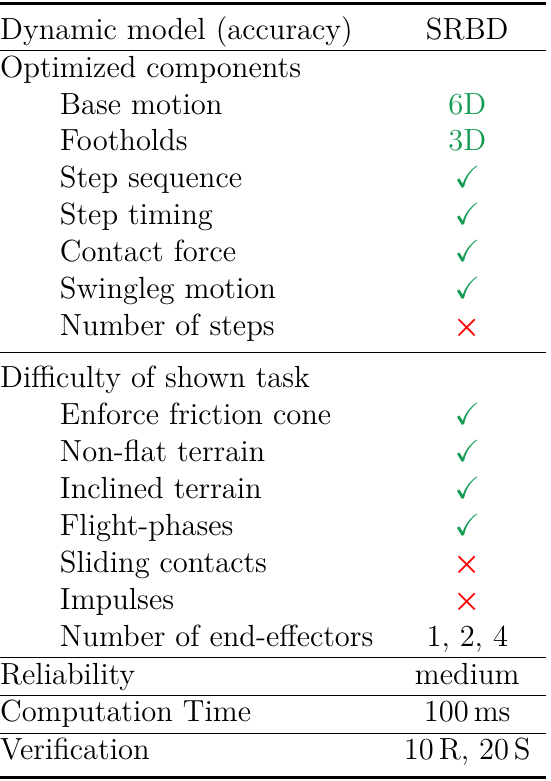


4
open-sourced software
Summary
Computation Time 100 ms
1s-horizon, 4-footstep motion for a quadruped



Software
Publications
+ co-authored various others with F. Farshidian, D. Pardo, M. Neunert, ...
\( 1^{\text{st}} \) author
open-sourced





Additional Material:
Centroidal Dynamics \(\Rightarrow \) Single Rigid Body Dynamics
Newton-Euler Equations
+ Assumption A2: Momentum produced by the joint velocities is negligible.
+ Assumption A3: Full-body inertia remains similar to the one in nominal configuration.

| (pos) | Assumptions | ||
|---|---|---|---|
| Rigid Body Dynamics (RBD) | A1 | ||
| Centroidal Dynamics (CD) | A1 | ||
| Single Rigid Body Dynamics (SRBD) | A1, A2, A3 | ||
| Linear Inverted Pendulum (LIP) | A1, A2, A3, A4, A5, A6 |

Cubic-Hermite Spline for \(\color{red}{f_{\{x,y,z\}}(t)}, \color{blue}{p_{\{x,y,z\}}(t)}\)

