Certifying Bimanual RRT Motion Plans in a Second





Alexandre Amice
Peter Werner
Russ Tedrake
Certifying Bimanual RRT Motion Plans in a Second

$$a^{T}(t)x + b(t) > 0,~ \forall x \in \mathcal{A}(t),~ t \in [0,1]$$
$$a^{T}(t)x + b(t) < 0,~ \forall x \in \mathcal{B}(t),~ t \in [0,1]$$
Find \(a(t)\), \(b(t)\) such that
| # of Sos Program | 25830 |
|---|---|
| Average Time to Certify Edge | 0.299 s |
| Time to Certify Goal Plan | 1.211 s |
Alexandre Amice
Peter Werner
Russ Tedrake




Motivation: Rigorous Collision Checking
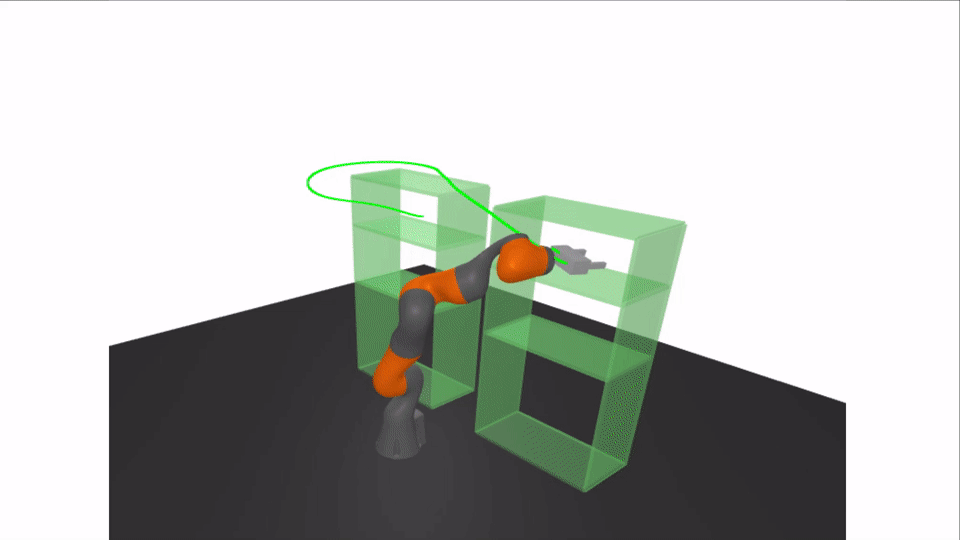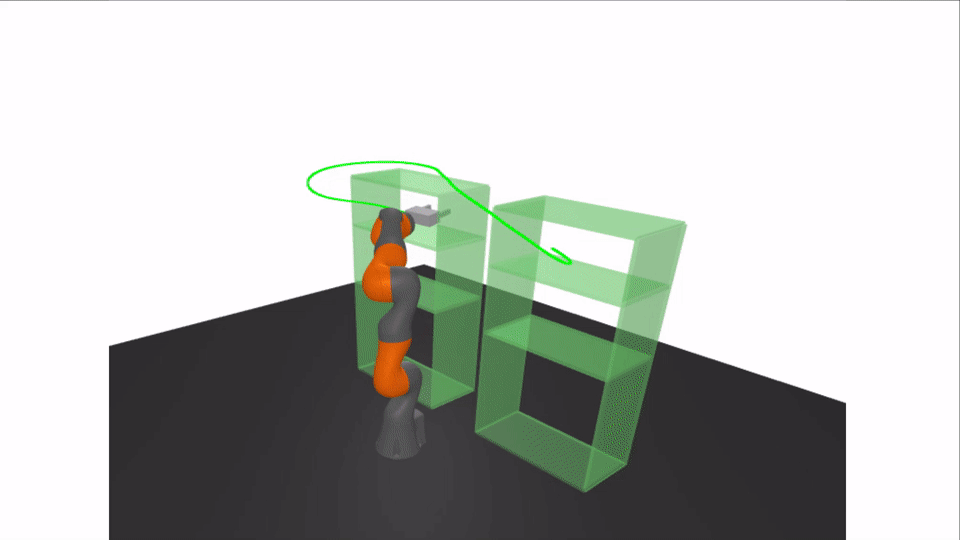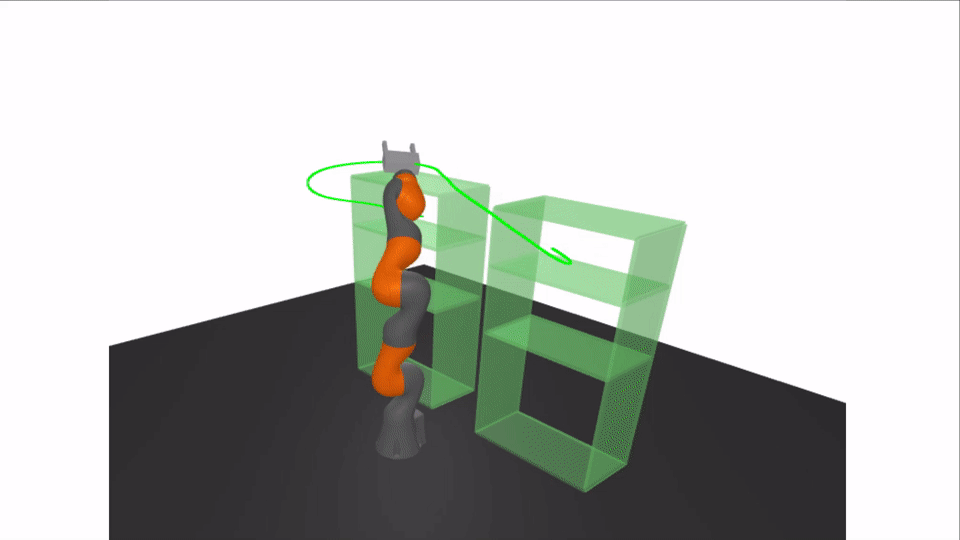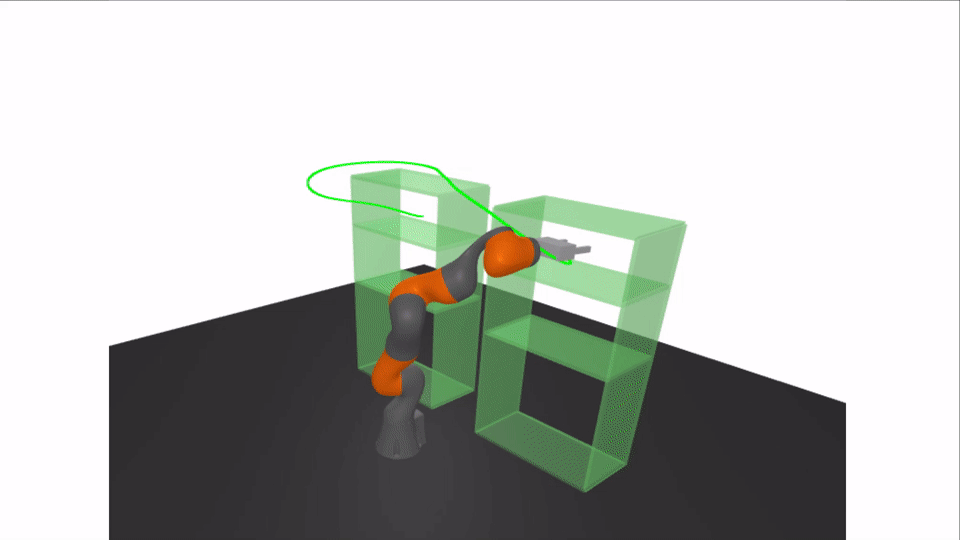






Motivation: Rigorous Collision Checking

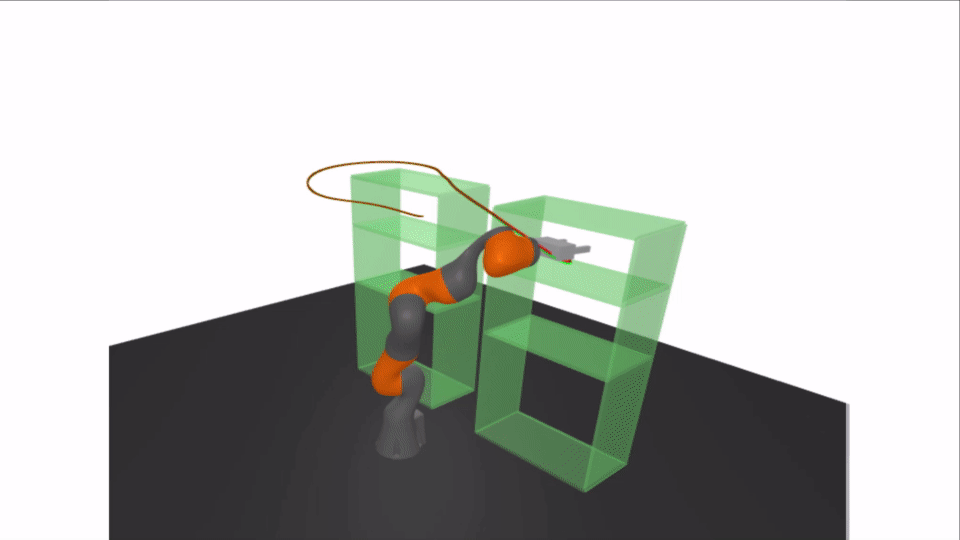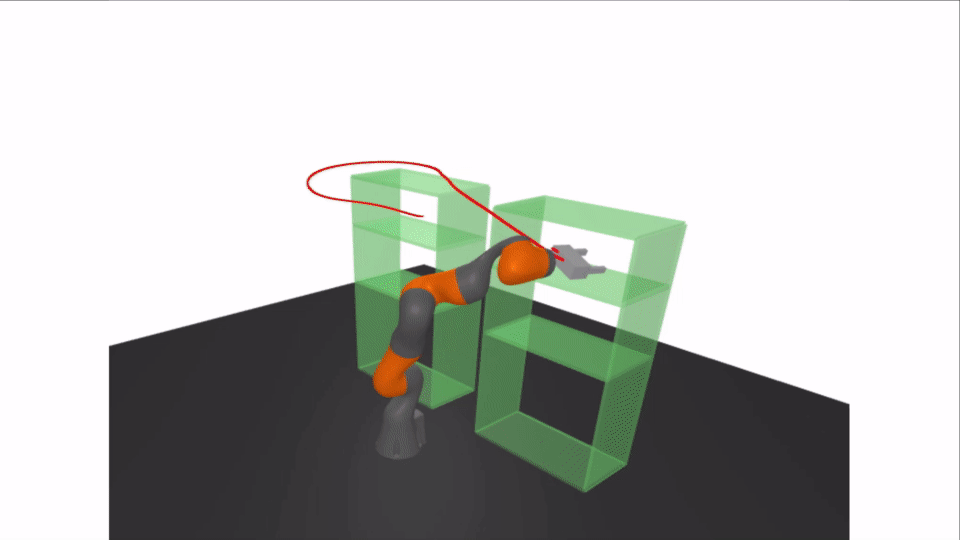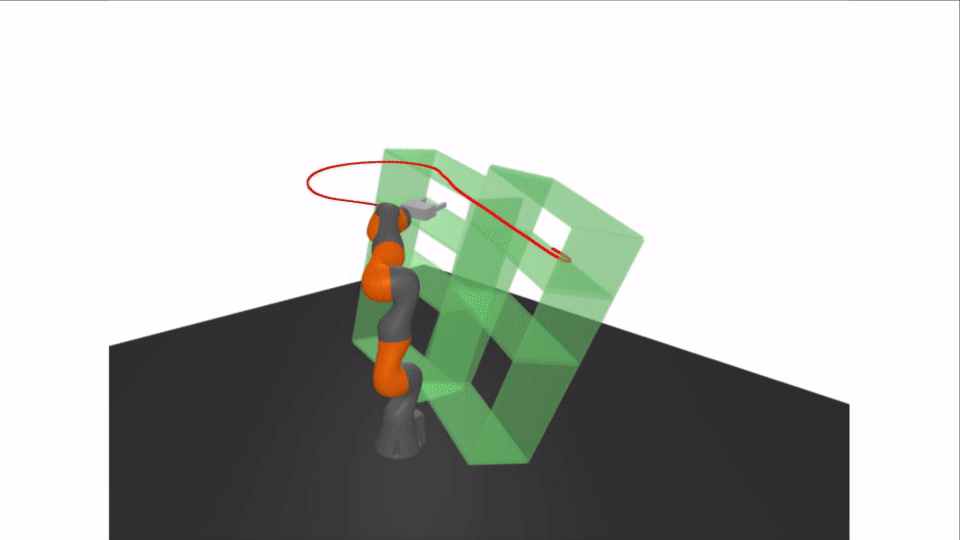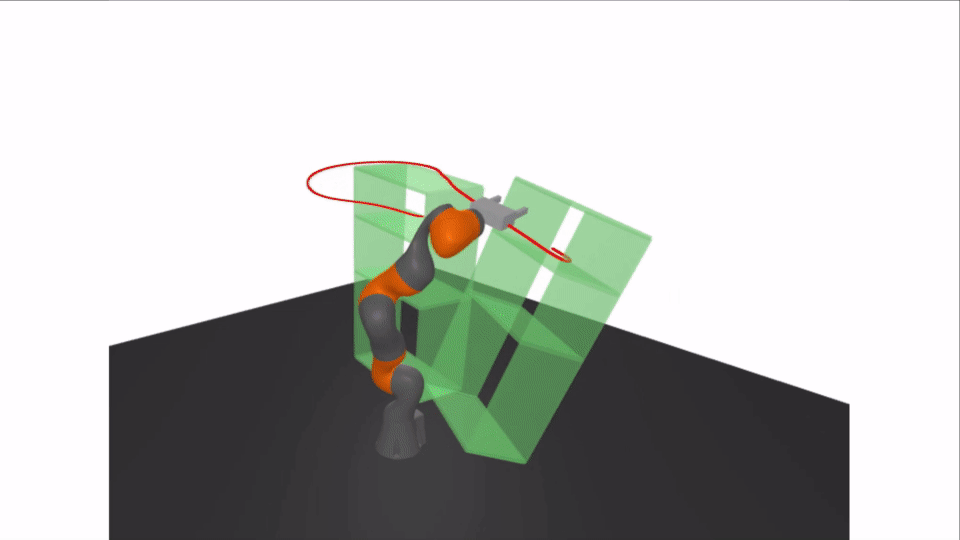


Motivation: Rigorous Collision Checking
-
Correct
-
Discriminating
-
General
-
Verifiable
-
Fast
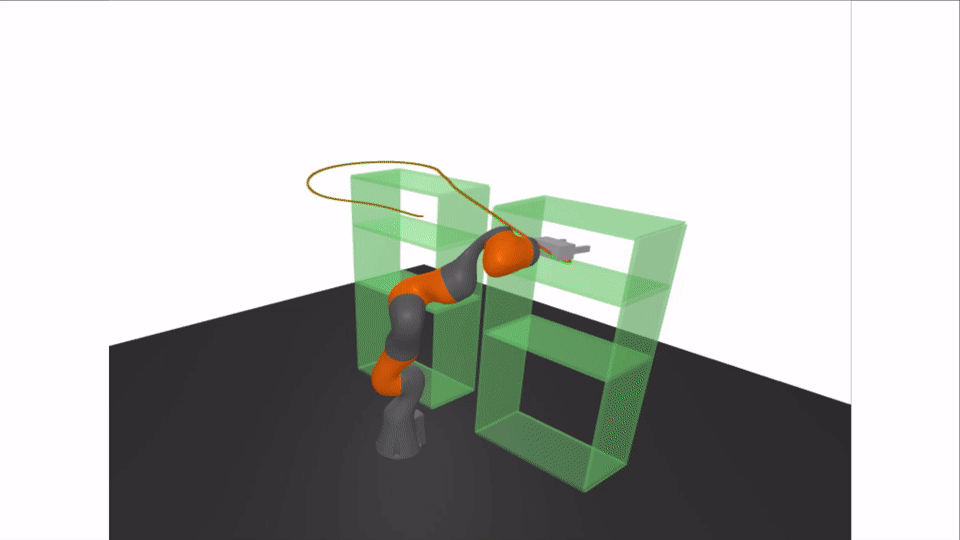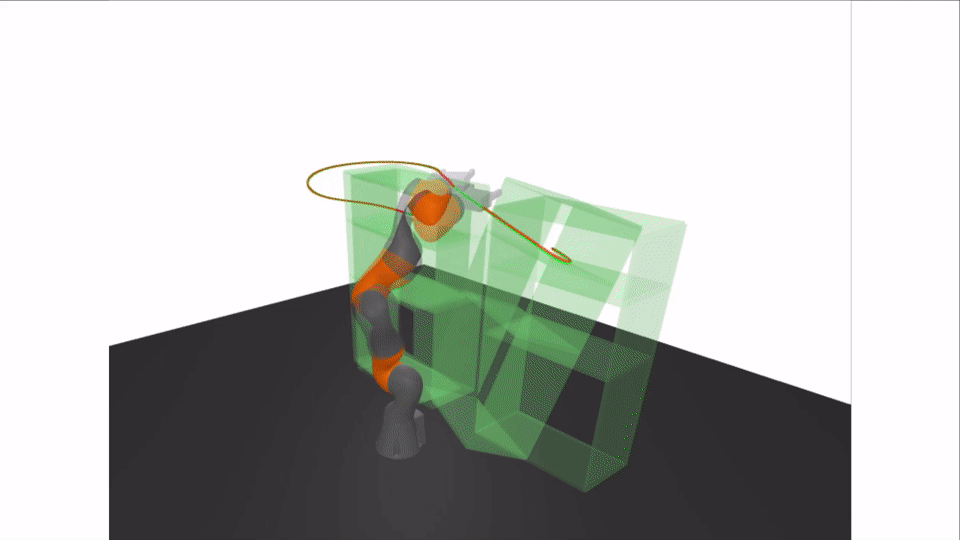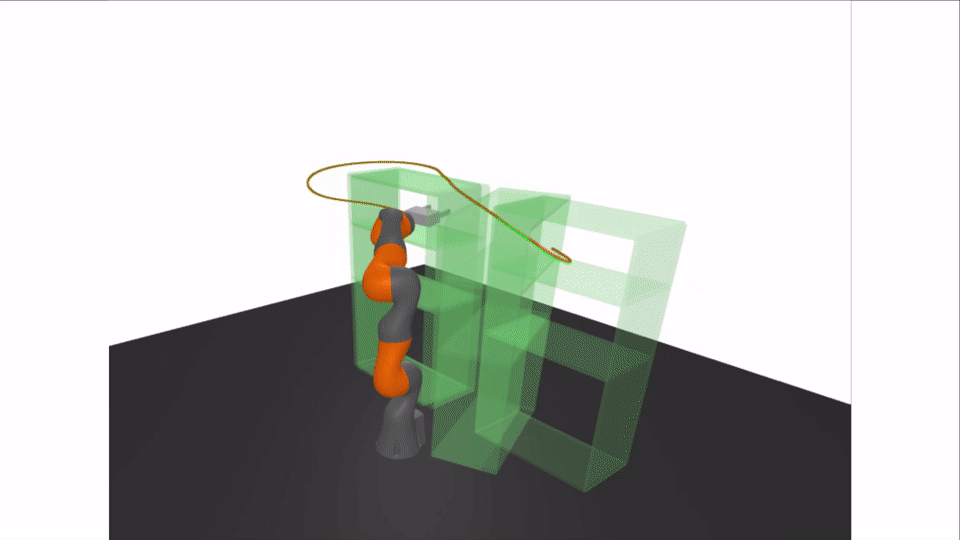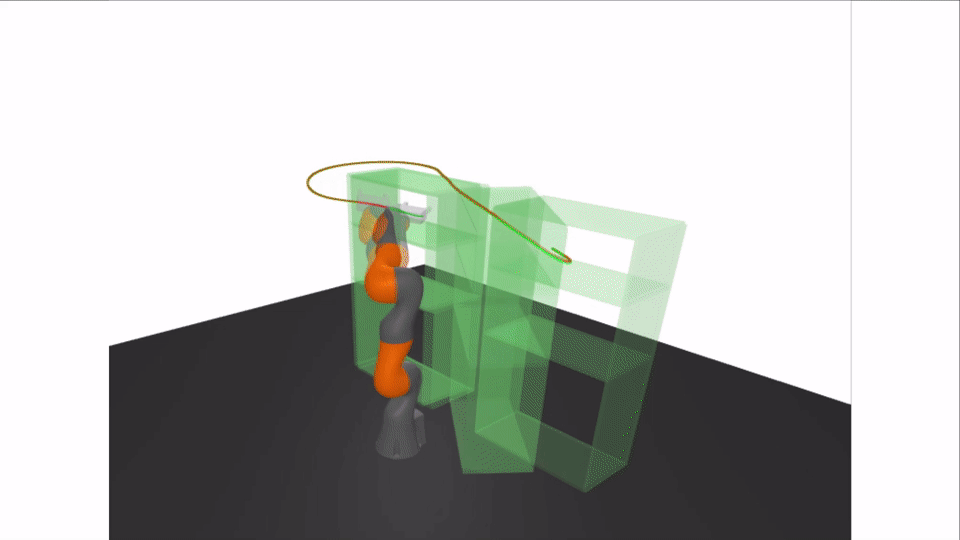
Results: Certifying A Bimanual RRT
| # Of RRT Edges | 105 |
|---|---|
| Average Time to Certify Edge | 0.299 s |
| Time to Certify Goal Plan | 1.211 s |

Results: Certifying Piecewise Cubic Paths
| # of Cubic Segments | 30 |
|---|---|
| Average Time to Certify a Segment | 0.317 s |
| Time to Certify Plan | 9.21 s |

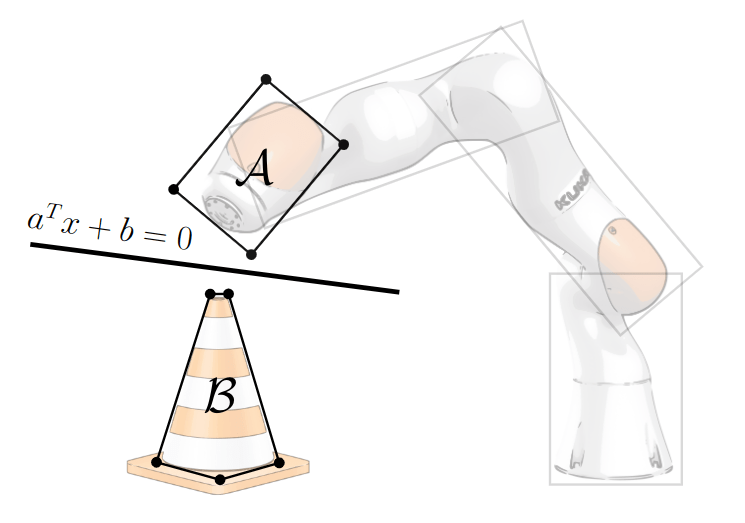
$$a^{T}x + b > 0,~ \forall x \in \mathcal{A}$$
$$a^{T}x + b < 0,~ \forall x \in \mathcal{B}$$
Find \(a\), \(b\) such that


Certifying Non-Collision

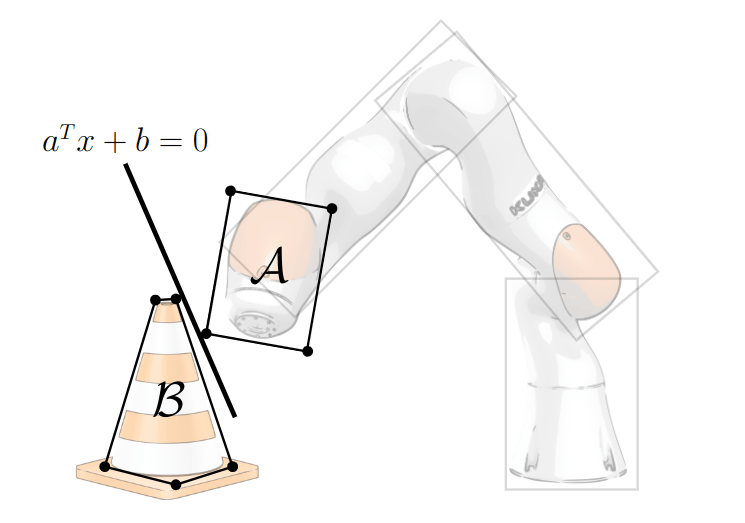
$$a^{T}x + b > 0,~ \forall x \in \mathcal{A}$$
$$a^{T}x + b < 0,~ \forall x \in \mathcal{B}$$
Find \(a\), \(b\) such that


Certifying Non-Collision


$$a^{T}(t)x + b(t) > 0,~ \forall x \in \mathcal{A}(t),~ t \in [0,1]$$
$$a^{T}(t)x + b(t) < 0,~ \forall x \in \mathcal{B}(t),~ t \in [0,1]$$
Find \(a(t)\), \(b(t)\) such that


Certifying Non-Collision


A Quick Primer on Sums-of-Squares
Definition: \(p(x)\) is SOS if \(p(x) = \sum_{i} q_{i}^{2}(x)\)
Example:
$$x^{4}-4x^{3}+5x^{2}+6x + 9 =$$
$$(x^{2}-2x)^{2} + (x+3)^{2} = $$
$$ \begin{bmatrix} 1 \\ x \\ x^{2} \end{bmatrix}^{T} \begin{bmatrix} 9 &3 & 0 \\3 & 5 & -2 \\ 0 & -2 & 1\end{bmatrix} \begin{bmatrix} 1 \\ x \\ x^{2}\end{bmatrix}$$


A Quick Primer on Sums-of-Squares
Definition: \(p(x)\) is SOS if \(p(x) = \sum_{i} q_{i}^{2}(x)\)
Example:
$$x^{4}-4x^{3}+5x^{2}+6x + 9 =$$
$$(x^{2}-2x)^{2} + (x+3)^{2} = $$
$$ \begin{bmatrix} 1 \\ x \\ x^{2} \end{bmatrix}^{T} \begin{bmatrix} 9 &3 & 0 \\3 & 5 & -2 \\ 0 & -2 & 1\end{bmatrix} \begin{bmatrix} 1 \\ x \\ x^{2}\end{bmatrix}$$
Theorem: \(p(x)\) is SOS if and only if \(\exists Q \succeq 0\) such that $$p(x) = \begin{bmatrix} 1 \\ x \\ \vdots \\ x^{d} \end{bmatrix}^{T} Q \begin{bmatrix} 1 \\ x \\ \vdots \\ x^{d} \end{bmatrix}$$
Checking the \(p(x)\) is SOS is a Convex, Semidefinite Program


A Quick Primer on Sums-of-Squares
Definition: \(p(x)\) is SOS if \(p(x) = \sum_{i} q_{i}^{2}(x)\)
Example: $$x^{4}-4x^{3}+5x^{2}+6x + 9 =$$ $$(x^{2}-2x)^{2} + (x+3)^{2} = $$
$$ \begin{bmatrix} 1 \\ x \\ x^{2} \end{bmatrix}^{T} \begin{bmatrix} 9 &3 & 0 \\3 & 5 & -2 \\ 0 & -2 & 1\end{bmatrix} \begin{bmatrix} 1 \\ x \\ x^{2}\end{bmatrix}$$
Theorem: \(p(x)\) is SOS if and only if \(\exists Q \succeq 0\) such that $$p(x) = \begin{bmatrix} 1 \\ x \\ \vdots \\ x^{d} \end{bmatrix}^{T} Q \begin{bmatrix} 1 \\ x \\ \vdots \\ x^{d} \end{bmatrix}$$


A Quick Primer on Sums-of-Squares
Definition: \(p(x)\) is SOS if \(p(x) = \sum_{i} q_{i}^{2}(x)\)
Theorem: \(p(x)\) is SOS if and only if \(\exists Q \succeq 0\) such that $$p(x) = \begin{bmatrix} 1 \\ x \\ \vdots \\ x^{d} \end{bmatrix}^{T} Q \begin{bmatrix} 1 \\ x \\ \vdots \\ x^{d} \end{bmatrix}$$
Checking the \(p(x)\) is SOS is a Convex, Semidefinite Program


Positive Functions on An Interval
Theorem (Markov-Lucasz): A univariate \(p(t) \geq 0 ~\forall t \in [0,1]\) if and only if there exists \(\lambda\) and \(\nu\) which are SOS such that $$p(t) = \begin{cases} \lambda (t) + t(1-t) \nu (t) & deg(p) = 2d \\ t \lambda (t) + (1-t) \nu (t) & \deg(p) = 2d + 1 \end{cases}$$
and
$$deg(\lambda) \leq 2d~~, deg(\nu)= \begin{cases} 2d-2 & deg(p) = 2d \\ 2d & deg(p) = 2d+1\end{cases}$$


Positive Functions on An Interval
Theorem (Markov-Lucasz): a univariate \(p(t) \geq 0 ~\forall t \in [0,1]\) if and only if there exists \(\lambda\) and \(\nu\) which are SOS such that $$p(t) = \begin{cases} \lambda (t) + t(1-t) \nu (t) & deg(p) = 2d \\ t \lambda (t) + (1-t) \nu (t) & \deg(p) = 2d + 1 \end{cases}$$
and
$$deg(\lambda) \leq 2d~~, deg(\nu)= \begin{cases} 2d-2 & deg(p) = 2d \\ 2d & deg(p) = 2d+1\end{cases}$$
$$a^{T}(t)x + b(t) > 0,~ \forall x \in \mathcal{A}(t),~ t \in [0,1]$$
$$a^{T}(t)x + b(t) < 0,~ \forall x \in \mathcal{B}(t),~ t \in [0,1]$$
Find \(a(t)\), \(b(t)\) such that



A Full Example: VPolytope
$$v_{1}$$
$$v_{2}$$
$$v_{3}$$
$$a^{T}x+b > 0$$
$$a^{T}x+b < 0$$


A Full Example
$$v_{1}$$
$$v_{2}$$
$$v_{3}$$
$$a^{T}x+b > 0$$
$$\Updownarrow \\ a^{T} (t) v_{i}(t) + b(t) \geq 1,~ t \in [0,1],~i=1,2,3$$
$$\Updownarrow \\ a^{T} (t) v_{i} (t) + b_{i} (t) -1 = \lambda (t) + t (1-t) \nu (t) \\ \lambda(t),~ \nu(t) \text{are SOS}$$
$$a^{T} (t) x + b(t) > 0, ~ \forall x \in \mathcal{A} (t), ~ t \in [0,1]$$




$$a^{T}_{\mathcal{A}, \mathcal{B}}(t)x + b_{\mathcal{A}, \mathcal{B}}(t) > 0,~ \forall x \in \mathcal{A}(t),~ t \in [0,1]$$
$$a^{T}_{\mathcal{A}, \mathcal{B}}(t)x + b_{\mathcal{A},\mathcal{B}}(t) < 0,~ \forall x \in \mathcal{B}(t),~ t \in [0,1]$$
Find \(a_{\mathcal{A},\mathcal{B}}(t)\), \(b_{\mathcal{A},\mathcal{B}} (t)\) such that
For all pairs \((\mathcal{A}, \mathcal{B})\)
Convex Optimization Programs whose only hyperparameter is the degree of the hyperplane
A Recipe for Certifying Non-Collision
Results: Certifying A Bimanual RRT
| # of Sos Program | 25830 |
|---|---|
| # Of RRT Edges | 105 |
| Average Time to Certify Edge | 0.299 s |
| Time to Certify Goal Plan | 1.211 s |
| Time to Certify Whole Tree | 31.5 s |

Results: Certifying Piecewise Cubic Paths
| # of Sos Program | 5160 |
|---|---|
| # of Cubic Segments | 30 |
| Average Time to Certify Edge | 0.307 s |
| Time to Certify Plan | 9.21 s |

Certifying Bimanual RRT Motion Plans in a Second





Alexandre Amice
Peter Werner
Russ Tedrake