Fundamentals of
Fractional calculus
Table of contents
-
Preliminaries
- Gamma function
- Beta function
-
Fractional calculus
- Introduction
- Fractional integral
- Fractional derivative
- Properties & Examples
- Applications
- Mathematical models
- Machine learning
Preliminaries
Gamma function: Definitions
-
For any \(x>0\)
$$\Gamma \left( x \right) = \int_0^\infty {s^{x - 1} e^{ - s} ds}$$
-
For all complex numbers \(z\) except the non-positive integers
$$\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n},$$
where \(\gamma\) is Euler–Mascheroni constant.
Gamma function: Definitions
-
For any \(x>0\) and \( \Re(z)>-1 \)
$${\displaystyle \Gamma (z,x)=x^{z}e^{-x}\sum _{n=0}^{\infty }{\frac {L_{n}^{(z)}(x)}{n+1}},}$$where \(L_n\) is generalized Laguerre polynomial of degree \(n\).
-
$$\Gamma(x+1) = x \Gamma(x)$$
-
$$x! = \Gamma(x+1)$$
-
$$\Gamma(n+1) = n!$$
-
$$\Gamma(x) = \frac{\Gamma(x+1)}{x}, x<0$$
Gamma function: Properties
Beta function: Definitions
|
For any \(\Re(x)>0\) and \( \Re(y)>0 \)
|
-
$$\mathrm {B} (x,y)=\mathrm {B} (y,x)$$
-
$$\mathrm {B} (x,y)={\frac {\Gamma (x)\,\Gamma (y)}{\Gamma (x+y)}}$$
-
$${\binom {n}{k}}={\frac {1}{(n+1)\mathrm {B} (n-k+1,k+1)}}$$
Beta function: Properties
Fractional Calculus
Fractional calculus: Introduction
$$\begin{aligned} \frac{\text{d}f(x)}{\text{d}x} = 2x \quad\longleftarrow f(x) &= x^2 \longrightarrow \quad \int f(x) dx = \frac{x^3}{3}+c_1\\ \frac{\text{d}^2f(x)}{\text{d}x^2} = 2 \quad\longleftarrow f(x) &= x^2 \longrightarrow \quad \int\int f(x) dx = \frac{x^4}{12}+c_1 x + c_2 \end{aligned}$$
What does \(\displaystyle \frac{\text{d}^{\frac{1}{2}}f(x)}{\text{d}x^{\frac{1}{2}}}\) mean?
Fractional calculus: Introduction
Fractional Calculus was born in 1695

Tautochrone Problem
finding the curve such that the time needed for a particle to descend from a given position to the bottom of the curve (assuming there is no friction) is independent of position.
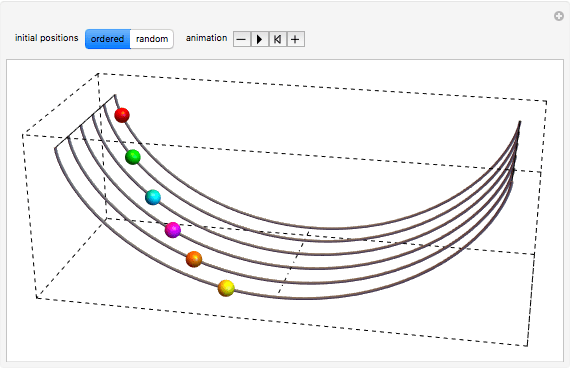
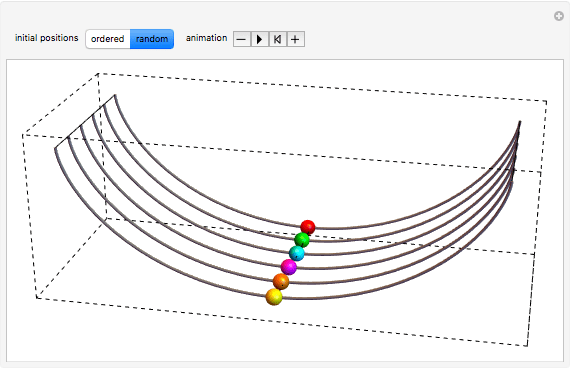
Fractional Calculus:
Fractional integral operator
Fractional integral operator: Preliminaries
Theorem. (Cauchy formula for repeated integration) Let \(f\) be some continuous function on the interval \([a, b]\). The \(nth\) repeated integral of \(f\) based at \(a\),
$$f^{(-n)}(x) = \int_a^x\int_a^{\sigma_1}\cdots\int_a^{\sigma_{n-1}} f(\sigma_n)d\sigma_n d\sigma_{n-1} \cdots d\sigma_{1},$$
is given by single integration:
$$f^{(-n)}(x) = \frac{1}{(n-1)!}\int_a^x (x-t)^{n-1} f(t) dt.$$
Fractional integral operator: Preliminaries
Proof. (by induction)
- For \(n=0\) we have: \(\int_a^x f(\sigma_1)\ d \sigma_1 =\frac{1}{0!}\int_a^x (x-t)^{0} f(t) dt.\)
- Suppose the statement holds for some arbitrary \(n\). Then for \(n+1\):
$$\begin{aligned}f^{(-(n+1))}(x)&=\displaystyle\int_{a}^{x} \int_{a}^{\sigma_{1}} \cdots \int_{a}^{\sigma_{n}} f\left(\sigma_{n+1}\right) d \sigma_{n+1} d \sigma_{n} \cdots d \sigma_{2} d \sigma_{1} \\&=\displaystyle\frac{1}{(n-1) !} \int_{a}^{x} \int_{a}^{\sigma_{1}}\left(\sigma_{1}-t\right)^{n-1} f(t) d t d \sigma_{1} \\ \quad&=\displaystyle\frac{1}{(n-1) !} \int_{a}^{x} \int_{t}^{x}\left(\sigma_{1}-t\right)^{n-1} f(t) d \sigma_{1} d t \\ \quad&=\displaystyle\frac{1}{(n) !} \int_{a}^{x}\left((x-t)^{n}-(t-t)^{n}\right) f(t) d t \\ \quad&=\displaystyle\frac{1}{(n) !} \int_{a}^{x}(x-t)^{n} f(t) d t \end{aligned}$$
Fractional integral operator: Definitions
Definition. (Riemann-Liouville Operator). Let \(f\) be a continuous function, \(\alpha \in \mathbb{R}^+\), and \(t \in \mathbb{R}\). The fractional integral of order \(\alpha\) is defined as:
$$J^{\alpha} f(t)=\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-u)^{\alpha-1} f(u) d u$$
Fractional integral operator: Definitions
Definition. (Hadamard Operator). Let \(f\) be a continuous function, \(\alpha \in \mathbb{R}^+\), and \(t \in \mathbb{R}\). The fractional integral of order \(\alpha\) is defined as:
$${\displaystyle _{a}J_{t}^{\alpha }f(t)={\frac {1}{\Gamma (\alpha )}}\int _{a}^{t}\left(\log {\frac {t}{\tau }}\right)^{\alpha -1}f(\tau ){\frac {d\tau }{\tau }},\qquad t>a\,.}$$
Fractional integral operator: Definitions
Definition. (Atangana–Baleanu Operator). Let \(f\) be a continuous function, \(\alpha \in \mathbb{R}^+\), \(t \in \mathbb{R}\) and \(AB(x)\) be a normalization function such that \(AB(0)=AB(1)=1\). The fractional integral of order \(\alpha\) is defined as:
$$_{a}^{AB}J_{t}^{\alpha }f(t)={\frac {1-\alpha }{AB(\alpha )}}f(t)+{\frac {\alpha }{AB(\alpha )\Gamma (\alpha )}}\int _{a}^{t}\left(t-\tau \right)^{\alpha -1}f(\tau )\,d\tau$$
Fractional Calculus:
Fractional differential operator
Fractional differential operator: Intuition
$$D^{1.5}f(t) = D^2J^{.5}f(t)\\D^{1.5}f(t) = J^{.5}D^2f(t)$$
Fractional differential operator: Definitions
Definition. (Riemann-Liouville operator) Pick some \(\alpha \in \mathbb{R}^+\), let \(n\) be the nearest integer greater than \(\alpha\). The Riemann-Liouville fractional derivative of order \(\alpha\) of a function \(f(t)\) is given by:
$$D_{RL}^{\alpha} f(t)=\frac{d^{n}}{d t^{n}} J^{n-\alpha} f(t)=\frac{1}{\Gamma(n-\alpha)} \frac{d^{n}}{d t^{n}} \int_{0}^{t}(t-u)^{n-\alpha-1} f(u) d u$$
Fractional differential operator: Definitions
Definition. (Caputo operator) Pick some \(\alpha \in \mathbb{R}^+\), let \(n\) be the nearest integer greater than \(\alpha\). The Caputo fractional derivative of order \(\alpha\) of a function \(f(t)\) is given by:
$$D_{C}^{\alpha} f(t)=J^{n-\alpha} \frac{d^{n}}{d t^{n}} f(t)=\frac{1}{\Gamma(n-\alpha)} \int_{0}^{t}(t-u)^{n-\alpha-1} f^{(n)}(u) d u$$
Fractional differential operator: Difference
For any \(c \in \mathbb{R}\):
- $$D_C^\alpha c = 0$$
- $$D_{RL}^\alpha c = \frac{cx^{-\alpha}}{\Gamma(1-\alpha)}$$
Fractional differential operator: Difference
Theorem. Let \(f\) be a continuous function, \(\alpha \in \mathbb{R}^+\) and \(n − 1 < \alpha < n\). Then:
$$D_{RL}^{\alpha} f(t)=D_{C}^{\alpha} f(t)+\sum_{k=0}^{n-1} \frac{f^{(k)}\left(0^{+}\right)}{\Gamma(1+k-\alpha)}(t)^{k-\alpha}$$
Fractional Calculus:
Properties
Fractional calculus: Properties
Let \(\alpha > 0, C, K \in \mathbb{R}\), and let \(f\) and \(g\) be functions such that their fractional derivatives and integrals exist. Then
- \(J^{\alpha}(C f(t)+K g(t)) =C J^{\alpha} f(t)+K J^{\alpha} g(t)\)
- \(D^{\alpha}(C f(t)+K g(t)) =C D^{\alpha} f(t)+K D^{\alpha} g(t)\)
- \(D_{C}^{\alpha}(C f(t)+K g(t)) =C D_{C}^{\alpha} f(t)+K D_{C}^{\alpha} g(t)\)
- $$D^\alpha D^\beta f(t) = D^{\alpha+\beta} f(t) = D^\beta D^\alpha f(t)$$
- $$J D^\alpha f(t) = D^\alpha J f(t) + \frac{f(0)}{\Gamma(\alpha)} t^{\alpha-1}$$
Fractional calculus: Examples
The fractional integral of order \(\alpha\) of \(1\) is given by
$$J^{\alpha} 1=\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-u)^{\alpha-1} d u=\frac{t^{\alpha}}{\alpha \Gamma(\alpha)}=\frac{t^{\alpha}}{\Gamma(\alpha+1)}$$
For \(nth\) order integral we have:
$$J^{n \alpha} 1=\frac{t^{n \alpha}}{\Gamma(n \alpha+1)}$$
Fractional calculus: Examples
Theorem. The Riemann-Liouville derivative of order \(\alpha > 0\) with \(n − 1 < \alpha < n\) of the function \(f(t) = t^p\) for \(p \ge 0\) is given by:
$$D^{\alpha} t^{p}=\frac{\Gamma(p+1)}{\Gamma(p-\alpha+1)} t^{p-\alpha}$$
Fractional calculus: Examples
Proof. We compute the Riemann-Liouville Derivative of power \(\alpha > 0\) as:
$$D^{\alpha} t^{p}=\frac{1}{\Gamma(n-\alpha)} \frac{d^{n}}{d t^{n}} \int_{0}^{t}(t-u)^{n-\alpha-1} u^{p} d u$$
Fractional calculus: Examples
Set \(u = vt\) for \(0 \le v \le 1\), \(du = tdv\) and we get:
$$\begin{aligned} D^{\alpha} t^{p}&=\frac{1}{\Gamma(n-\alpha)} \frac{d^{n}}{d t^{n}} \int_{0}^{1}((1-v) t)^{n-\alpha-1}(v t)^{p} t d v\\ &=\frac{1}{\Gamma(n-\alpha)} \int_{0}^{1}(1-v)^{n-\alpha-1} v^{p} d v \frac{d^{n}}{d t^{n}} t^{n+p-\alpha} \\ &=\frac{1}{\Gamma(n-\alpha)} B(p+1, n-\alpha) \frac{d^{n}}{d t^{n}} t^{n+p-\alpha} \\ &=\frac{1}{\Gamma(n-\alpha)} B(p+1, n-\alpha) \frac{\Gamma(n+p-\alpha+1)}{\Gamma(p-\alpha+1)} t^{p-\alpha} \\ &=\frac{1}{\Gamma(n-\alpha)} \frac{\Gamma(p+1) \Gamma(n-\alpha) \Gamma(n+p-\alpha+1)}{\Gamma(n+p-\alpha+1)} \frac{1}{\Gamma(p-\alpha+1)} t^{p-\alpha} \\ &=\frac{\Gamma(p+1)}{\Gamma(n-\alpha+1)} t^{p-\alpha} \end{aligned}$$
Applications
Applications:
Mathematical models
Applications: ODEs
For any \(t\ge0\) the Lane-Emden equation is defined as:
- Ordinal:
$$y''(t)+\frac{2}{t}y'(t)+y^m(t)=g(t)$$
- Fractional:
$$D^\alpha y+\frac{2}{t}D^\beta y+y^m(t)=g(t)$$
where \(1<\alpha\le2,0<\beta\le1\).
Applications: PDEs
For any \(t\ge0\) the fractional Burgers equation is defined as:
$$\frac{\partial^\alpha u}{\partial t^\alpha} +\varepsilon u\frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2} - \eta \frac{\partial^\beta u}{\partial x^\beta}$$
where \(0<\alpha,\beta\le1\) and \(\varepsilon,\eta,\nu\) are some parameters.
Applications: IEs
For any \(t\ge0\) the Volterra's population model is defined as:
- Ordinal:
$$\kappa u'(t) = u(t) - u(t)^2 - u(t) \int_0^t u(x) dx,$$
- Fractional:
$$\kappa D^\alpha u = u(t) - u(t)^2 - u(t) \int_0^t u(x) dx,$$
where \(0<\alpha\le1\) and \(\kappa\) is a parameter.
Applications:
Machine learning
Applications: Machine learning
Neural Ordinary differential equations
$$\frac{\text{d}h(t)}{\text{d}t} = f(h(t),t,\theta)$$

Applications: Machine learning
Accelerating Neural ODEs with
Spectral Elements
$$\begin{aligned} \min _{\theta \in \mathbb{R}^{m}} \quad&\int_{t_{0}}^{t_{1}} L(t, x(t)) d t\\ s.t. \quad&\dot{x}(t)=f(t, x(t), u(t) ; \theta)\\ s.t. \quad&x\left(t_{0}\right)=x_{0} \end{aligned}$$

Applications: Machine learning
Fractional Hopfield Neural Networks: Fractional Dynamic Associative Recurrent Neural Networks

Applications: Machine learning
Dynamics Analysis of a New Fractional-Order Hopfield Neural Network with Delay and Its Generalized Projective Synchronization

Applications: Machine learning
Fractional-order gradient descent learning of BP neural networks with Caputo derivative
$$w_{new}= w_{old} - \eta \frac{\text{d}^\alpha L}{\text{d}\theta^\alpha}$$
