Gradient Descent

Suppose a man is at top of the valley and he wants to get to the bottom of the valley. So he goes down the slope.

He decides his next position based on his current position and stops when he gets to the bottom of the valley which was his goal.

The Idea

Take repeated steps in the opposite direction of the gradient of the function at the current point.

The Idea

Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function.

Formal Definition

It performs two steps iteratively:

Compute the slope (gradient) that is the first-order derivative of the function at the current point
Move-in the opposite direction of the slope increase from the current point by the computed amount

The Algorithm

Consider some continuously differentiable real-valued function $f: \mathbb{R} \rightarrow \mathbb{R}$.

Using a Taylor expansion we obtain

$$f(x + \epsilon) = f(x) + \epsilon f'(x) + \mathcal{O}(\epsilon^2).$$

Pick a fixed step size $\eta > 0$, and choose $\epsilon = -\eta f'(x)$:

$$f(x - \eta f'(x)) = f(x) - \eta f'^2(x) + \mathcal{O}(\eta^2 f'^2(x)).$$

Mathematical Formulation

If $f'(x) \neq 0$, with a small enough $\eta$ we have:

$$f(x - \eta f'(x)) \lessapprox f(x).$$

This means that, if we use

$$x \leftarrow x - \eta f'(x)$$

to iterate $x$, the value of function $f$ might decline.

Mathematical Formulation

Repeat the iterations until

At most $N$ iterations.
When magnitude of the gradient $|f'(x)|$ is small enough
When the function converged $|f(x_{n+1}) - f(x_n)| < \xi$

Stopping Criteria

Implementation

import numpy as np

def f(x):
    return x**2

def df(x):
    return 2 * x

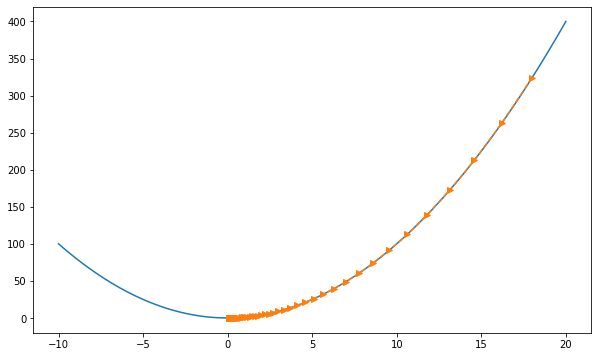
a, b = -10, 20  # optimization domain
eta = 0.05  # learning rate
max_iterations = 53
x = 18 # x_initial

history = [x]  # save function values
for epoch in range(max_iterations):
    x = x - eta * df(x) # x = x - eta * df/dx
    history.append(x)

print('final x =', x)

Visualization

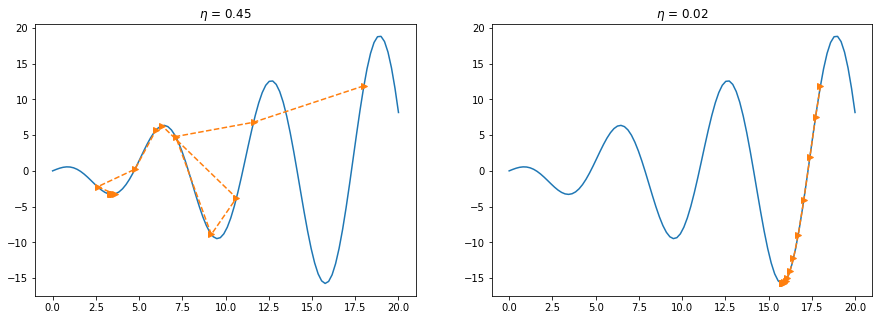
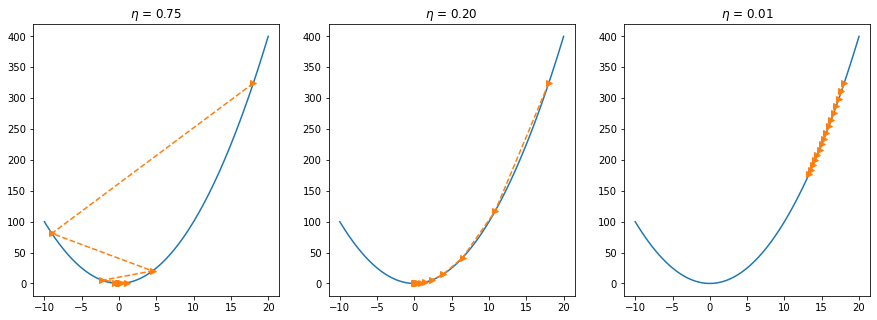
Step Size

If we use an excessively high learning rate, $\mathcal{O}(\eta^2 f'^2(x))$ might become significant. Hence we cannot guarantee that the iteration of $x$ will be able to lower the value of $f(x)$.

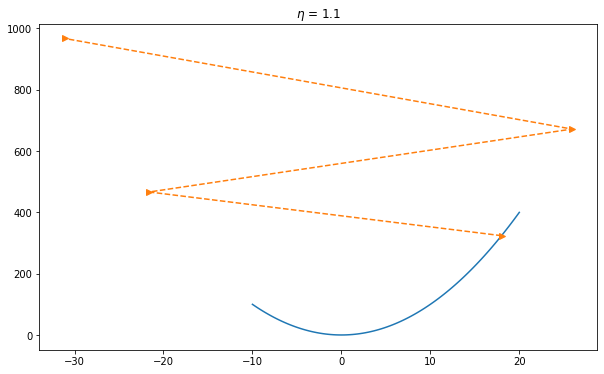
Local Minimum

Multivariate Gradient Descent

Suppose $\mathbf{x} = [x_1, x_2, \ldots, x_d]^\top$ and objective function $f: \mathbb{R}^d \to \mathbb{R}$. The gradient will be defined as:

$$\nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top.$$

Here the Taylor approximation takes the form

$$f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \mathbf{\boldsymbol{\epsilon}}^\top \nabla f(\mathbf{x}) + \mathcal{O}(\|\boldsymbol{\epsilon}\|^2).$$

The corresponding gradient descent iteration:

$$\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x}).$$

In Machine Learning

Many of the machine learning models use gradient descent on their core:

Perceptron algorithm
Linear & Logistic Regression
Ridge, Lasso & Elastic Net Regression/Classification
Neural Networks & Deep Learning

Types of Gradient Descent

Batch gradient descent
Stochastic gradient descent
Mini-batch gradient descent

Batch Gradient Descent

Vanilla gradient descent, aka batch gradient descent, computes the gradient of the cost function w.r.t. to the parameters $\theta$ for the entire training dataset

$$\theta = \theta - \eta \cdot \nabla_\theta J( \theta)$$

for i in range(n_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

BATCH GRADIENT DESCENT

Takes the average of the gradients of all the training examples for updating parameters.
Just one step of gradient descent in one epoch.
It is great for convex or relatively smooth error manifolds.
It can be very slow and is intractable for datasets that don't fit in memory.

Stochastic Gradient Descent

Stochastic gradient descent (SGD) in contrast performs a parameter update for each training example $x^{(i)}$ and label $y^{(i)}$:

$$\theta = \theta - \eta \cdot \nabla_\theta J( \theta; x^{(i)}; y^{(i)})$$

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

STOCHASTIC GRADIENT DESCENT

It is usually much faster and can also be used to learn online.
It converges faster when the dataset is large
It performs frequent updates with a high variance that cause the objective function to fluctuate heavily.
SGD's fluctuation, enables it to jump to new and potentially better local minima.

Mini-Batch Gradient Descent

Mini-batch gradient descent finally takes the best of both worlds and performs an update for every mini-batch of $n$ training examples:

$$\theta = \theta - \eta \cdot \nabla_\theta J( \theta; x^{(i:i+n)}; y^{(i:i+n)})$$

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

MINI-BATCH GRADIENT DESCENT

It reduces the variance of the parameter updates, which can lead to more stable convergence
it can make use of highly optimized vectorized optimizations

Challenges

Choosing a proper learning rate can be difficult. A learning rate that is too small leads to painfully slow convergence, while a learning rate that is too large can hinder convergence and cause the loss function to fluctuate around the minimum or even to diverge.

Challenges

Learning rate schedules try to adjust the learning rate during training by e.g. annealing, i.e. reducing the learning rate according to a pre-defined schedule or when the change in objective between epochs falls below a threshold. These schedules and thresholds, however, have to be defined in advance and are thus unable to adapt to a dataset's characteristics.

Challenges

Additionally, the same learning rate applies to all parameter updates. If our data is sparse and our features have very different frequencies, we might not want to update all of them to the same extent, but perform a larger update for rarely occurring features.

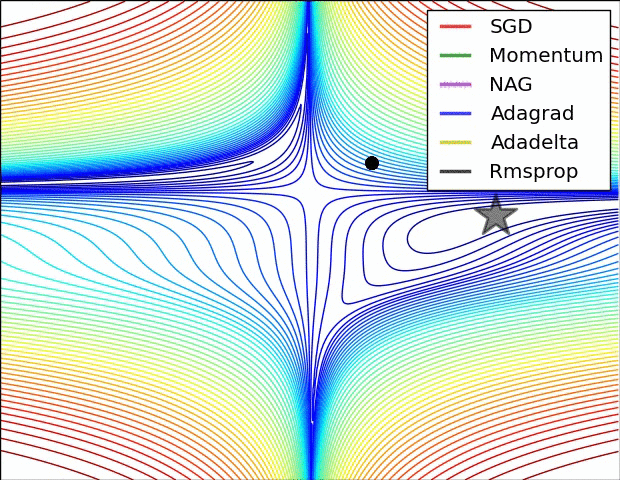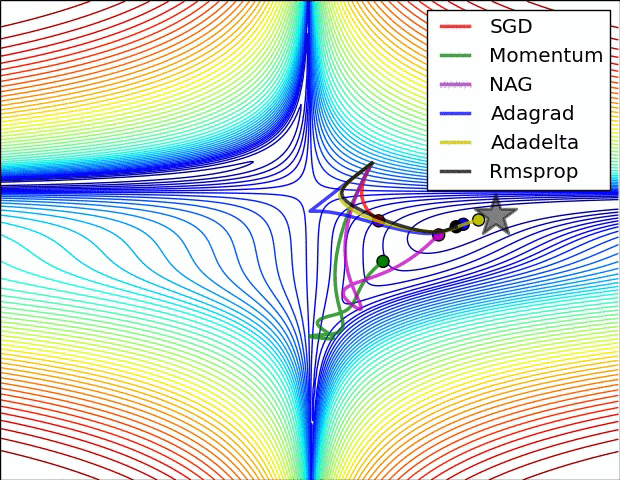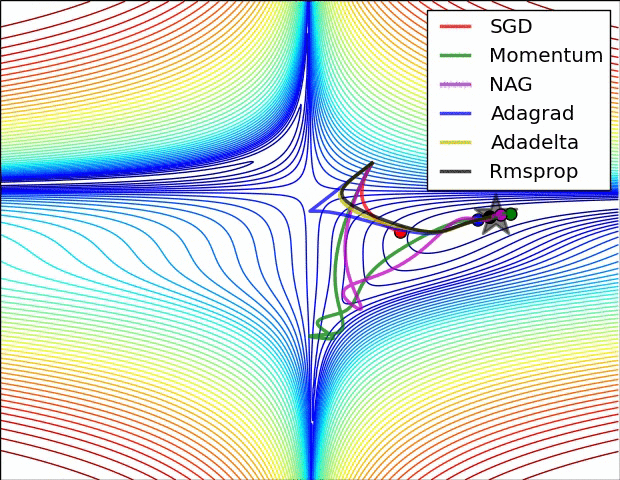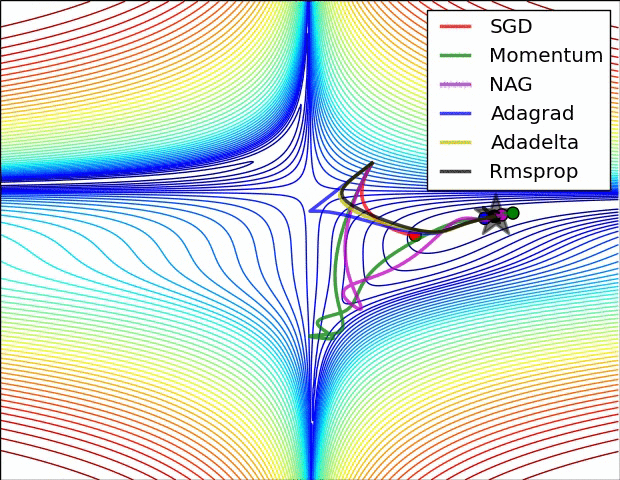
Advanced Methods

Momentum
Nesterov
Adagrad
Adadelta
RMSprop
Adam
AMSGrad
AdamW
QHAdam
AggMo

Comparison of Methods

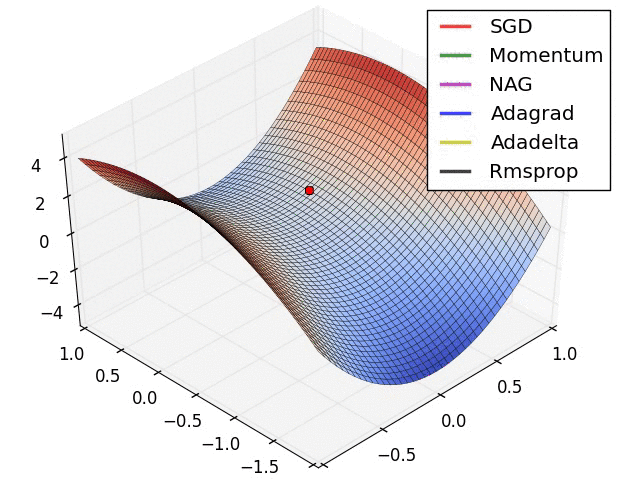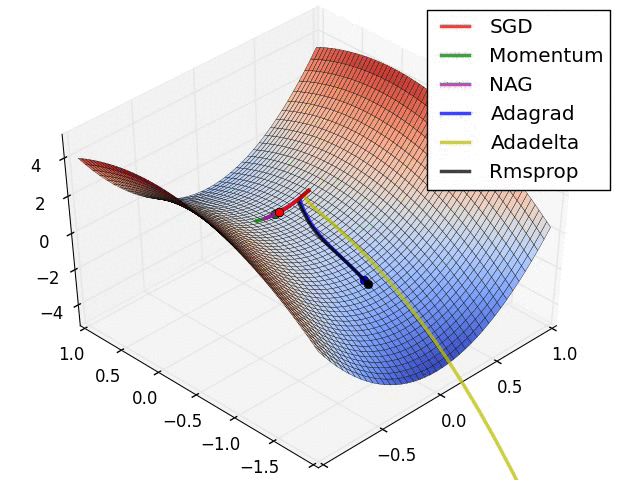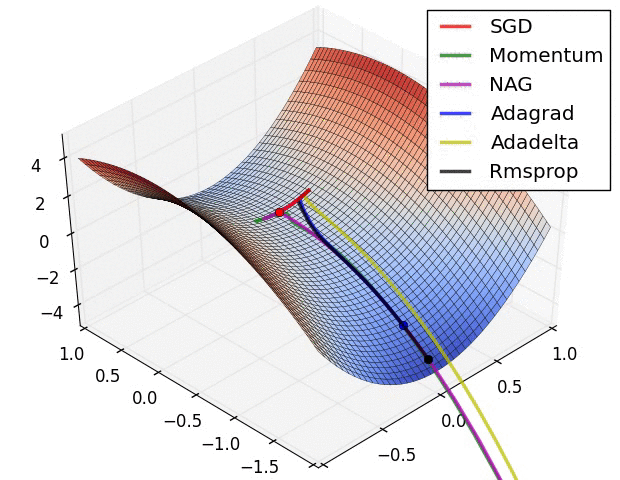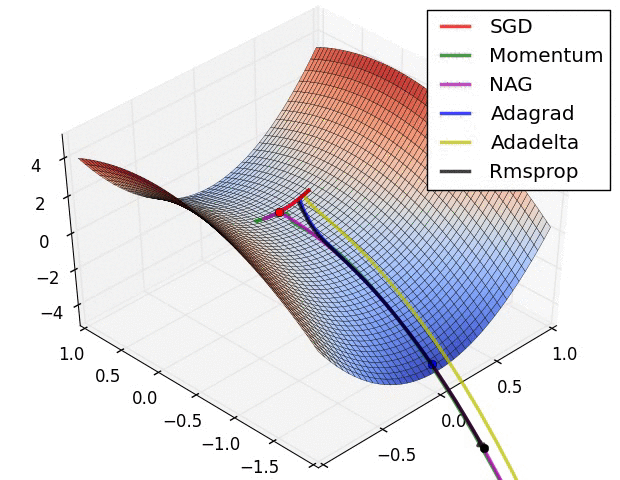
Resources

https://d2l.ai/chapter_optimization/gd.html
https://ruder.io/optimizing-gradient-descent/
https://towardsdatascience.com/batch-mini-batch-stochastic-gradient-descent-7a62ecba642a
https://raghumeka.github.io/CS289ML/gdnotes.pdf