DIVE INTO

Artificial Neural Networks

Alireza Afzal Aghaei

M.Sc student at SBU

Overview

  • Introduction
  • Biological neural networks
    • Neuron
  • Artificial neural networks
    • Backpropagation
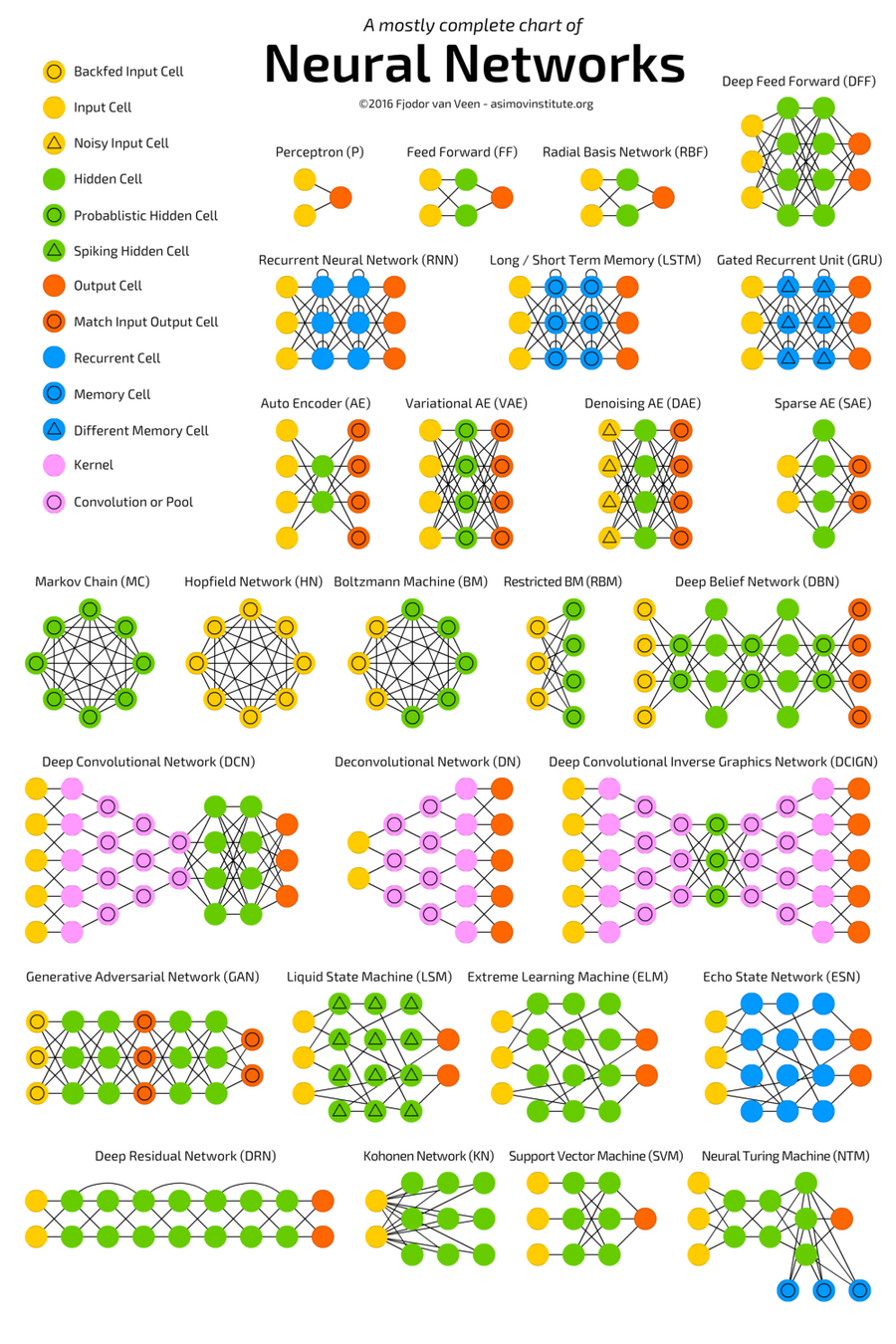
  • Other types of ANN
    • CNN
    • RNN
    • LSTM
  • Some Examples

Types of learning

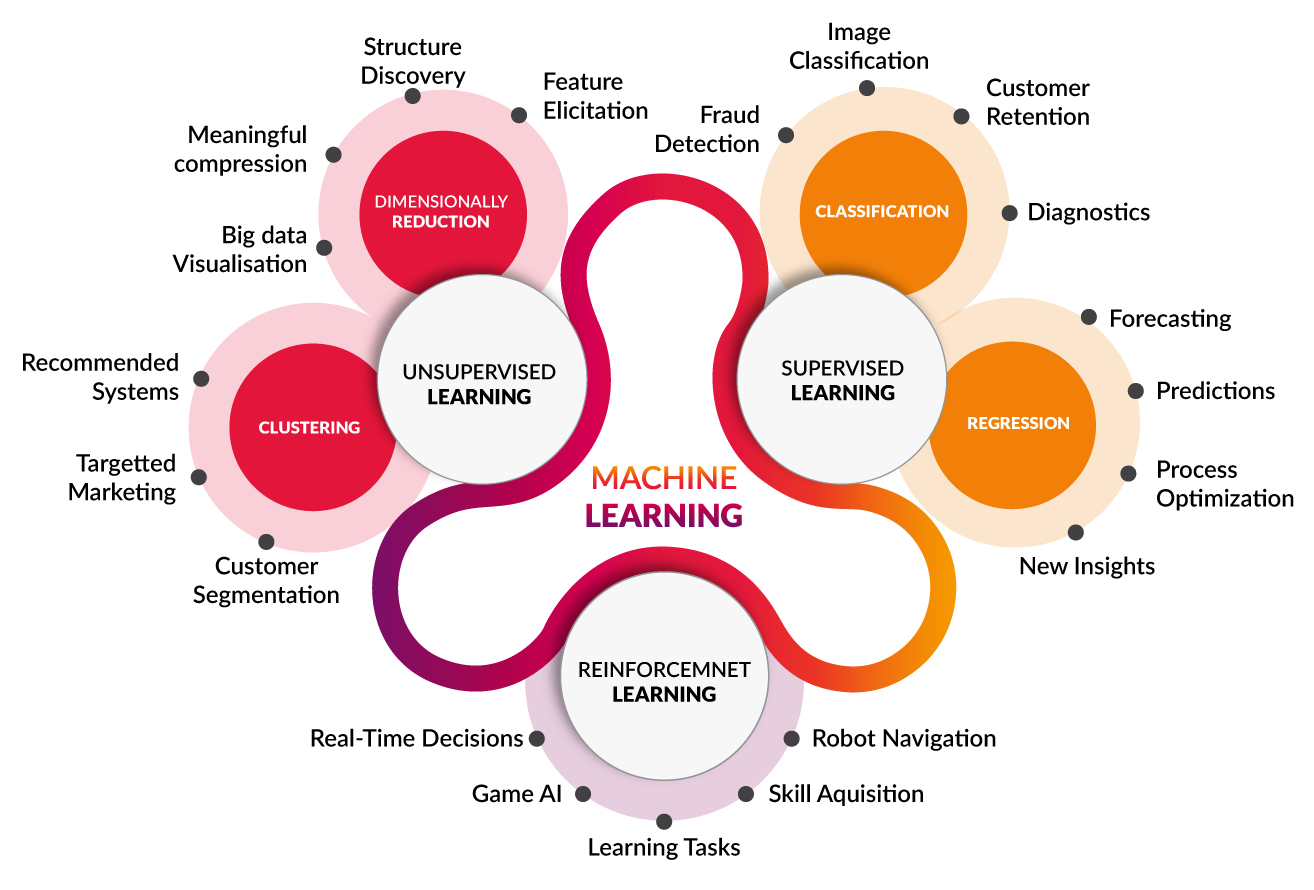
Types of learning

offline learning vs online learning

The motivation of studies in neural networks lies in the flexibility and power of information processing that conventional computing machines do not have

Motivation

Whats ANN?

  • Artificial Neural Network is an information-processing system that has certain performance characteristics in common with biological neural networks

 

  • It have been developed as generalizations of mathematical models of human cognition or neural biology

How it works?

Information processing occurs at many simple elements called neurons.

How it works?

  1. Signals are passed between neurons over connection links
  2. Each connection link has an associated weight
  3. Each neuron applies an activation function to its net input
  4. Each neuron returns new output signal

Biological Neural Networks

LET'S DIVE INTO BIOLOGY

nEURON

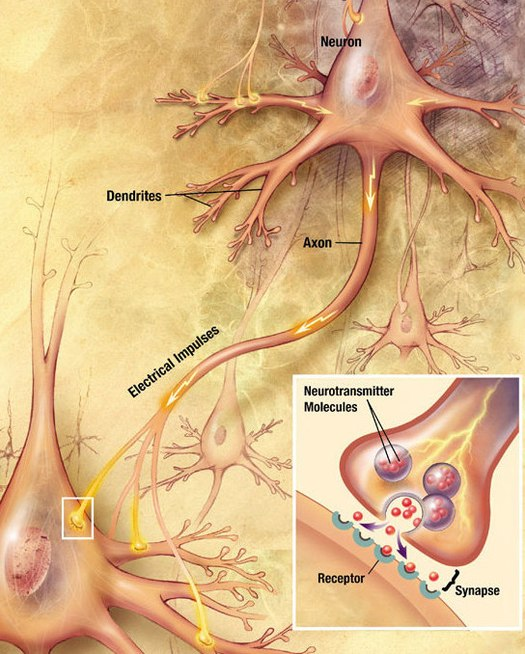
A neuron, is an electrically excitable cell that receives, processes, and transmits information through electrical and chemical signals

nEURON

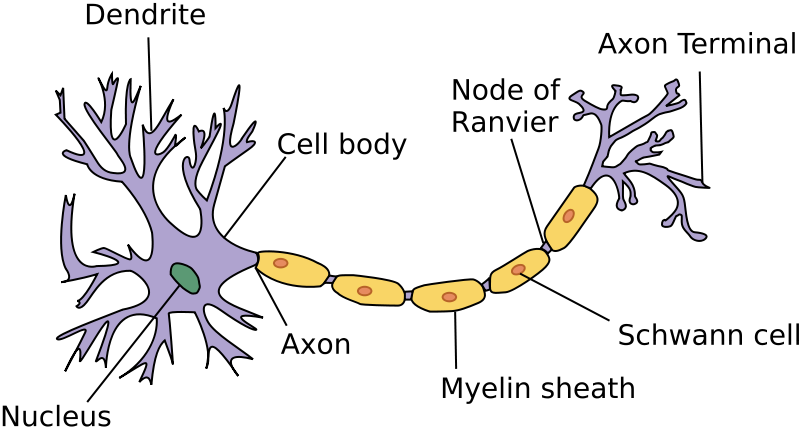
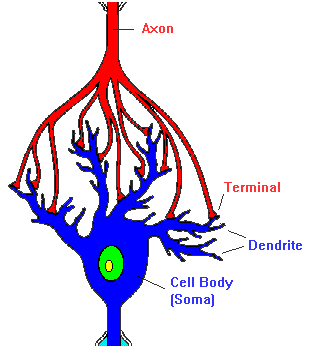
nEURON Structure

  • Dendrites
  • Soma
  • Axon

Dendrites

  • Tree-like structure
  • Receives signal from surrounding neurons
  • Dendritic spine: increase the surface area of the dendrite to receive more information

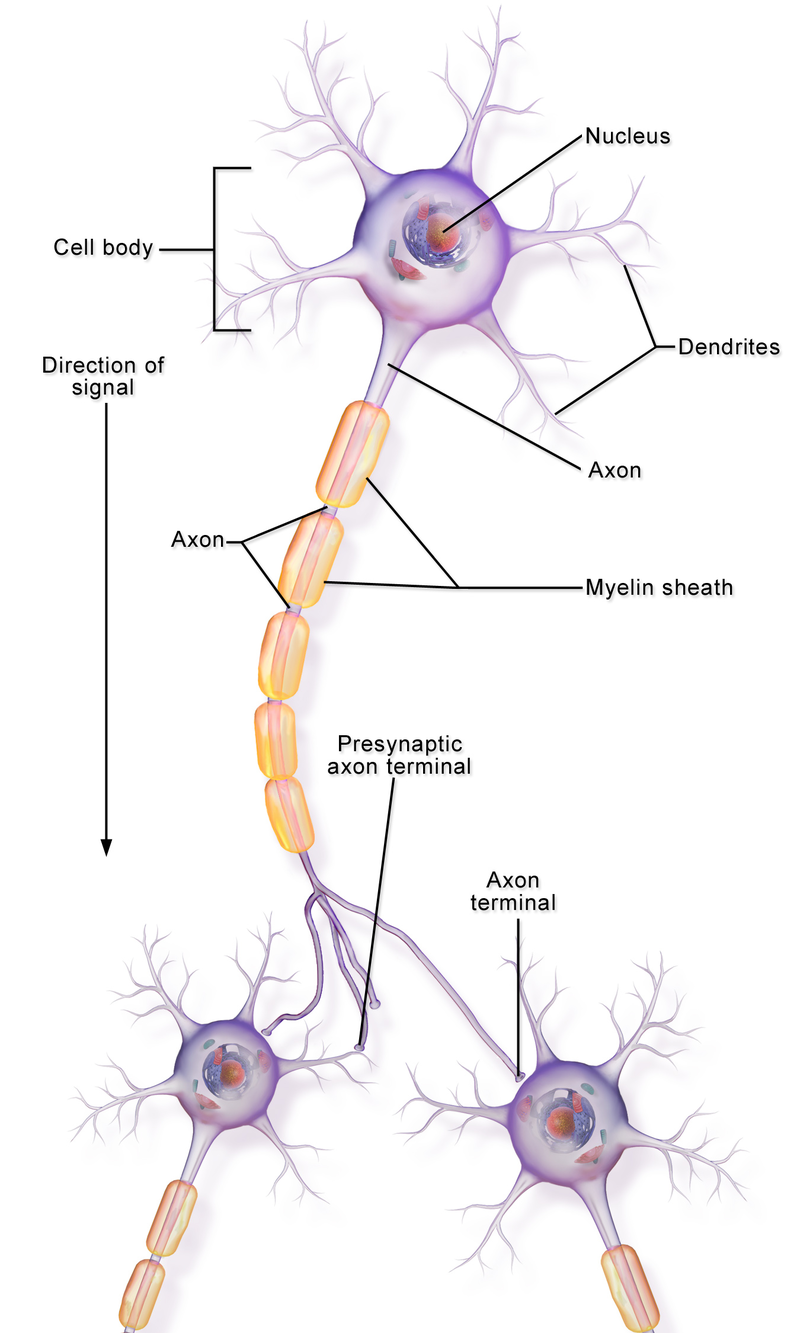
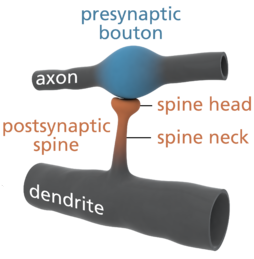
Axon & Myelin

  • Axon is a thin cylinder that transmits the signal from one neuron to others.
  • Myelin insulates nerve cell axons to increase the speed at which signal travels from one nerve cell body to another

SYNAPSE

  • Gaps between two neuron
  • Synaptic plasticity
  • Synapse's strength may be modified by experience

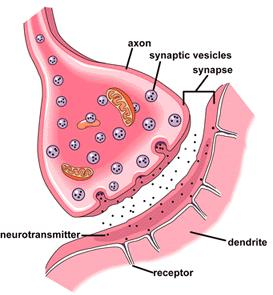
excitation & inhibition

  • Excitatory signaling from one cell to the next makes the latter cell more likely to fire

 

  • Inhibitory signaling makes the latter cell less likely to fire

Hebb Rule

the connection between the two neurons is strengthened when both neurons are active at the same time

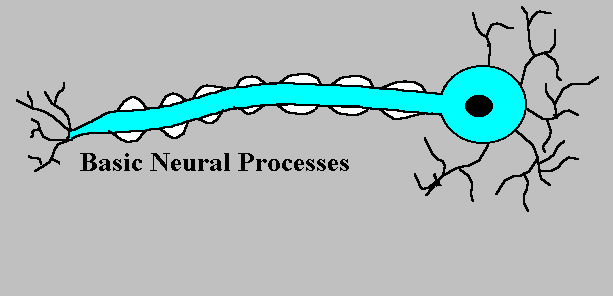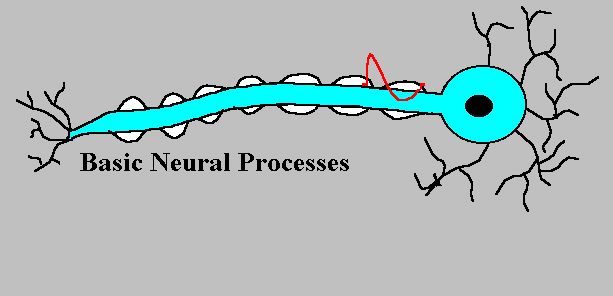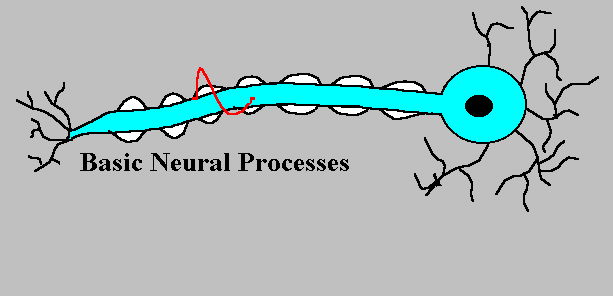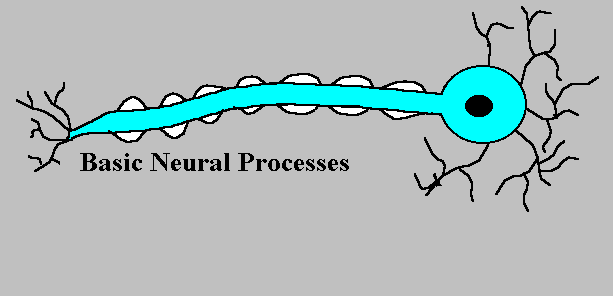
neuron signal transmission 

Other kind of neurons

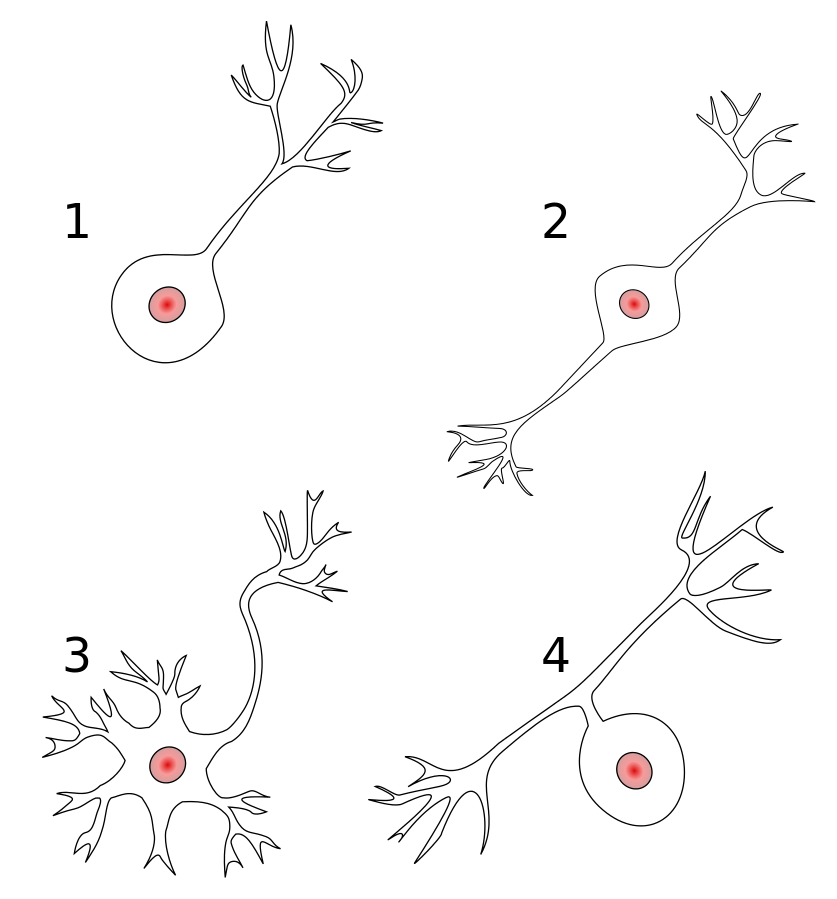
  1. Unipolar
  2. Bipolar
  3. Multipolar
  4. Pseudounipolar

Summary

  • Dendrite: It receives signals from other neurons

  • Soma: It sums all the incoming signals to generate input

  • Axon: When the sum reaches a threshold value, neuron fires

  • Synapses: The point of interconnection of one neuron with other neurons

  • The connections can be inhibitory or excitatory  in nature

  • Hebb rule

Summary

So, neural network, is a highly interconnected network of billions of neuron with trillion of interconnections between them

Further reading

Artificial Neural Networks

LET'S DIVE INTO ARTIFICIAL NEURAL NETWORKS

Analogy of ANN with BNN

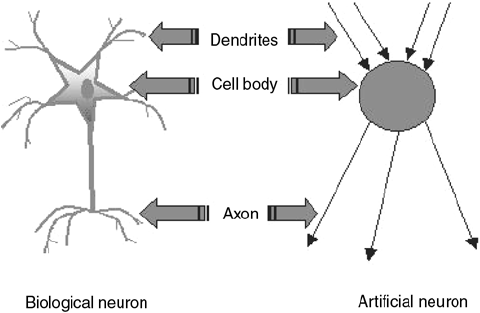
ANALOGY OF ANN WITH BNN

Criteria BNN ANN
Processing Massively parallel, slow
Massively parallel, fast but inferior than BNN
Size 10 11 neurons and 10 15 interconnections Depends
Learning Tolerate ambiguity Precise
Fault tolerance robust Performance degrades with partial damage
Storage synapse Continuous  memory

Artificial Neuron Structure

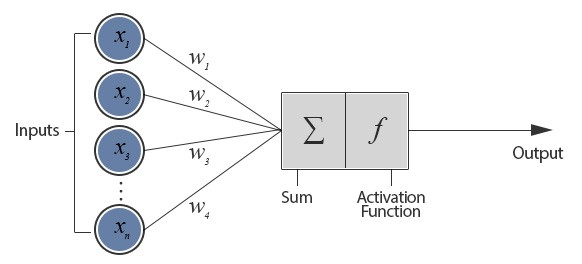
we call this artificial neuron perceptron

ARTIFICIAL NEURon STRUCTURE

  • Weight represents the strength of the interconnection
  • Sum corresponds to any numerical value from 0 to infinity
  • Threshold is set to limit the response to arrive at desired value

ACTIVATION FUNCTIONS

Can we use any arbitrary activation function?

  • continuos
  • differentiable
  • monotonically non-decreasing
  • derivative should be easy to compute

Activation functions: Identity

f(x)=x
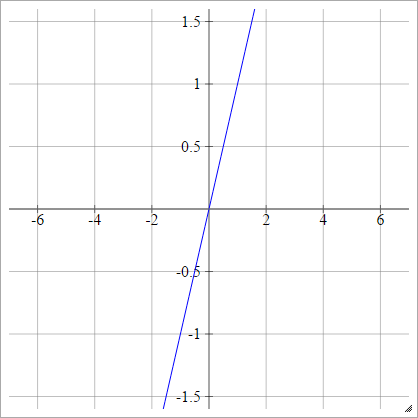
  • Bad idea!

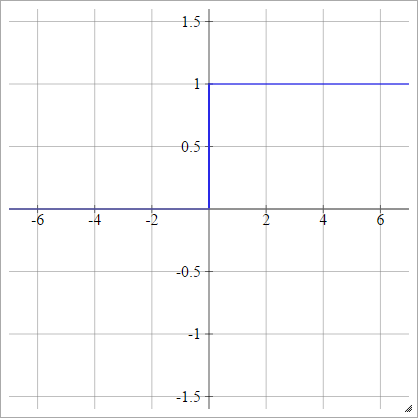
Activation functions: step

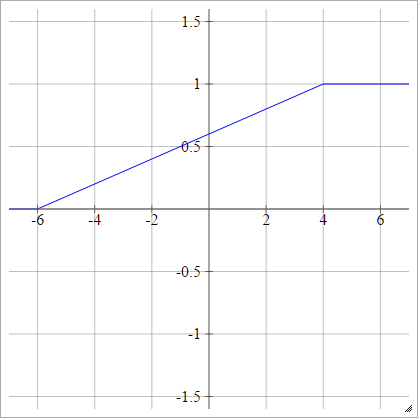
f(x)=\left\{ \begin{array}{ll} 1 & x \ge 0 \\ 0 & x \lt 0 \\ \end{array} \right.

Activation functions: Piecewise Linear

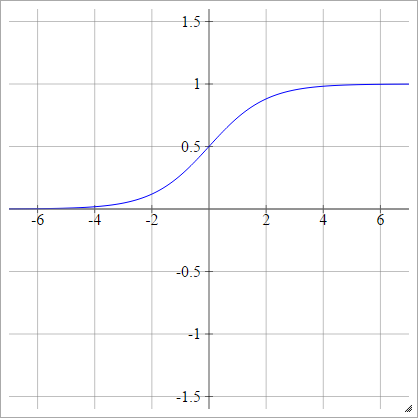
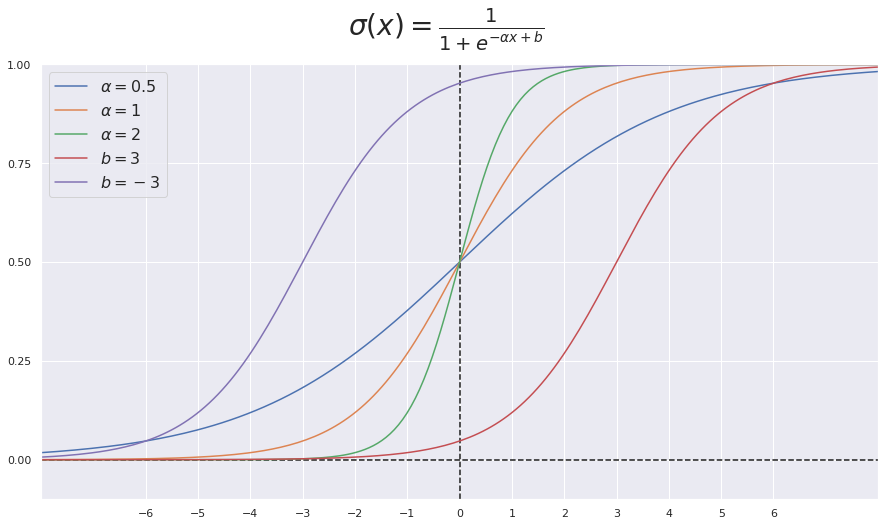
f(x) = \begin{cases} 0 & x < a \\ mx+z & a \leq x \leq b \\ 1 & x > b \end{cases}

Activation functions: Sigmoid

f(x)=\frac{1}{1+e^{-\alpha x}}

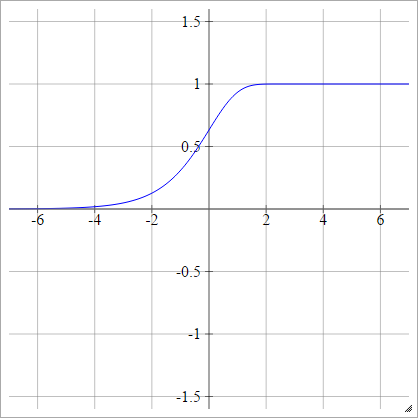
Activation functions: Piecewise Linear

f(x) = 1 − e^{−e^x}

Activation functions: Bipolar

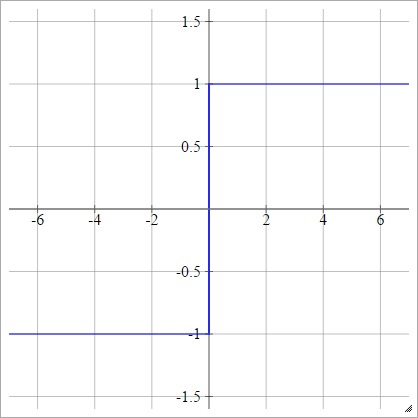
f(x)=\left\{ \begin{array}{ll} +1 & x \gt 0 \\ -1 & x \lt 0 \\ \end{array} \right.

Activation functions: Bipolar Sigmoid

f(x)= \frac{1-e^{-x}}{1+e^{-x}}

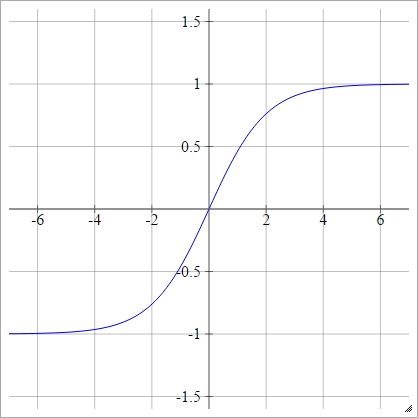
Activation functions: Tanh

f(x)=tanh(x) = 2\ sigmoid(2x) - 1

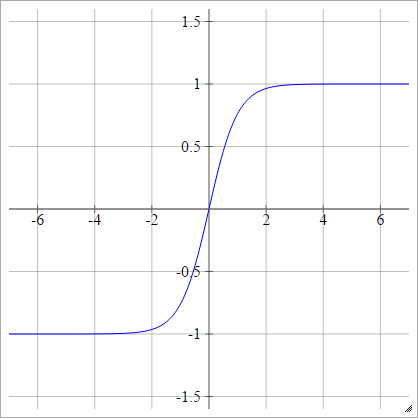
Activation functions: LeCun's Tanh

f(x) = 1.7159 \ tanh( \frac{2}{3} x)

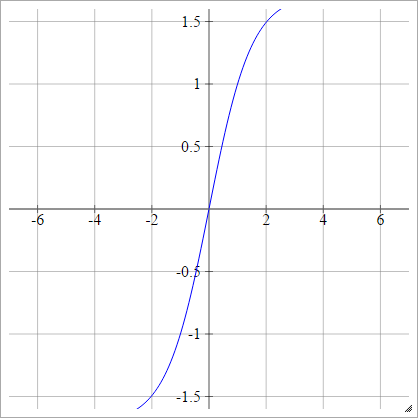
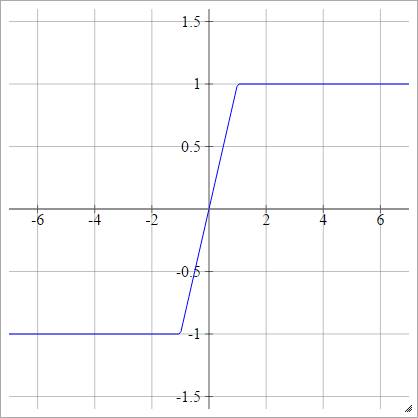
Activation functions: Hard Tanh

f(x) = \max(-1, \min(1, x))

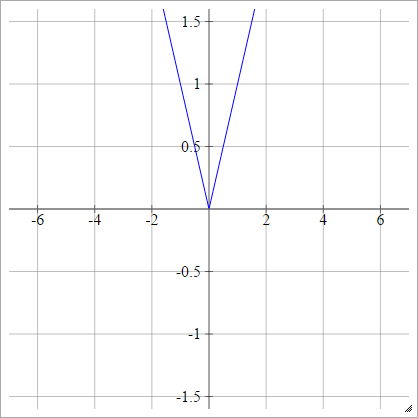
Activation functions: Absolute

f(x) = \mid x \mid

Activation functions: Relu

f(x)=max(0,x)

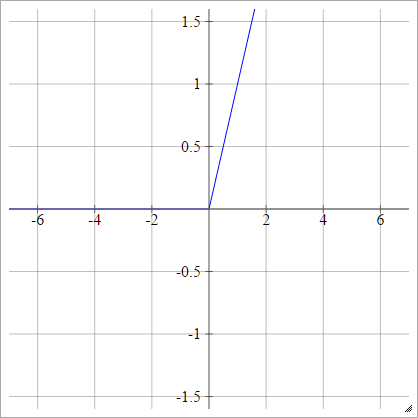
Why ReLU is Non linear?

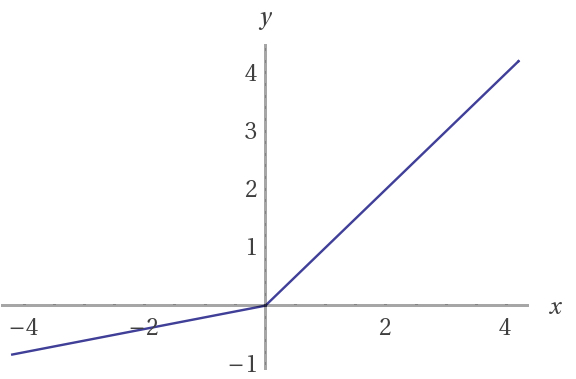
Activation functions: Leaky ReLU

f(x)=max(0.1x,x)

For negative X the gradient go towards 0 so the weights will not get adjusted during gradient descent

Activation functions: Relu

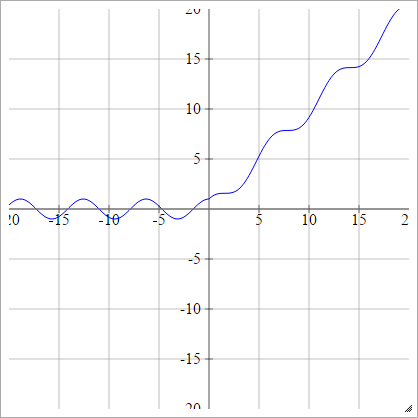
It has proved that 6 times improvement in convergence from Tanh function

Activation functions: Relu

f(x) = \max(0, x)+\cos(x)

Activation functions: Gaussian

f(x) = e^{-\frac{1}{2} x^2}

Activation functions:Multiquadratic

f(x) = \sqrt{(x-x_0)^2 + y_0^2}

Activation functions:Softmax

f(\vec v) = \frac{e^{\vec v}}{\sum\limits_{i=1}^{n} e^{v_i}}

Sigmoid function used for the two-class classification

Softmax function is used for the multi-class classification

Other Activation functions

  • SWISH
  • Cosine
  • Maxout
  • Inverse Multiquadratic

SIDE NOTEs about Activation functions

  • Vanishing gradient problem
  • Zero centered output

Bias

Bias allows us to shift the activation function to the left/right

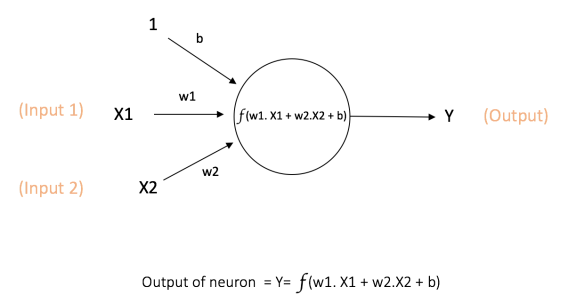
Bias

Let's see some Examples

f(x)=\left\{ \begin{array}{ll} 1 & x \ge 0 \\ 0 & x \lt 0 \\ \end{array} \right.
  • Activation function: 

NOT GATE

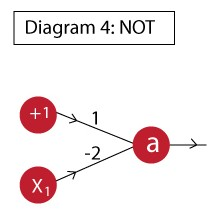
f(x)=\left\{ \begin{array}{ll} 1 & x \ge 0 \\ 0 & x \lt 0 \\ \end{array} \right.
  • Activation function: 

OR GATE

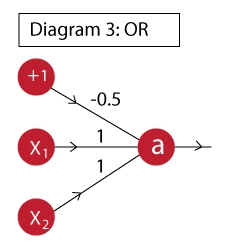
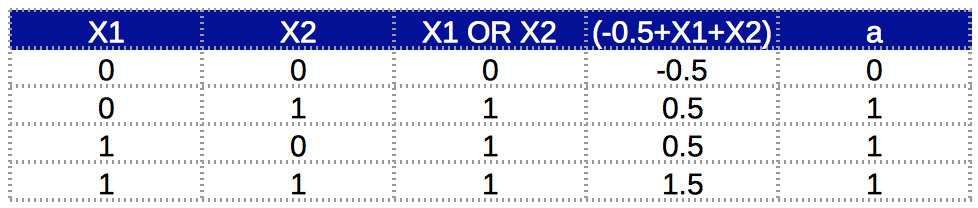
f(x)=\left\{ \begin{array}{ll} 1 & x \ge 0 \\ 0 & x \lt 0 \\ \end{array} \right.
  • Activation function: 

And GATE

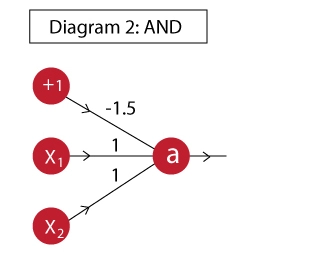
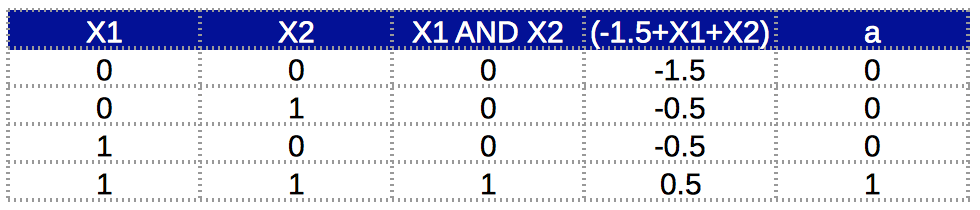
f(x)=\left\{ \begin{array}{ll} 1 & x \ge 0 \\ 0 & x \lt 0 \\ \end{array} \right.
  • Activation function: 

A' . B' GATE

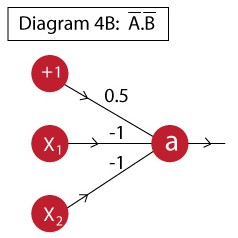
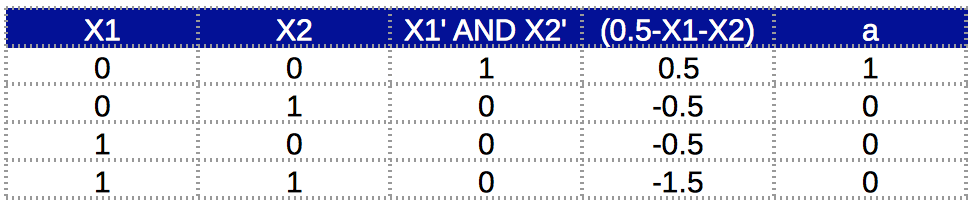
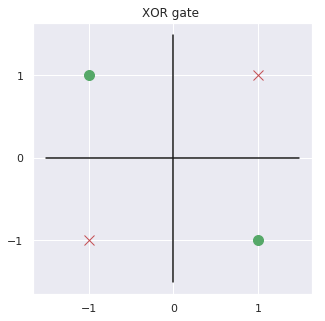
XNOR GATE

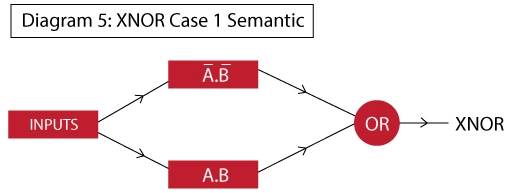
\begin{aligned} \overline{A \oplus B} & = \overline{[(A + B)\cdot \ (\bar{A}+\bar{B})]} \\ & = [ \overline{A + B} + \overline{\bar{A} + \bar{B}}] \\ &= (\bar{A} \cdot \bar{B}) \ + (A \cdot B) \end{aligned}

XNOR GATE

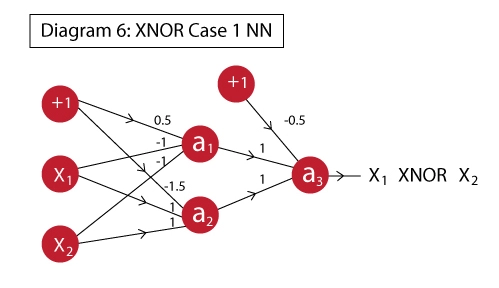
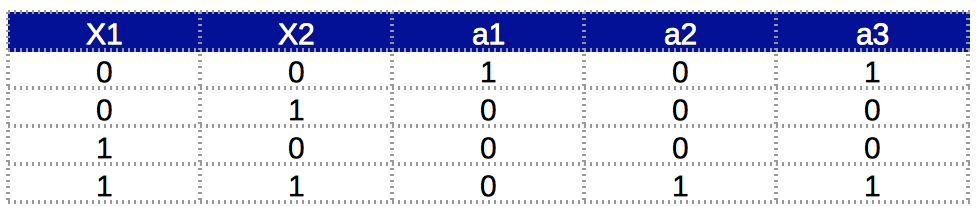
Network architecture is not unique!

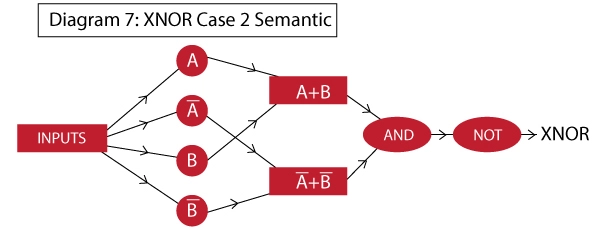
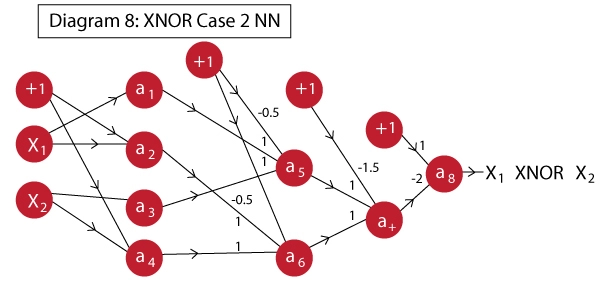
Seams easy, Nah?

Oh wait!

How can we find the weights?!

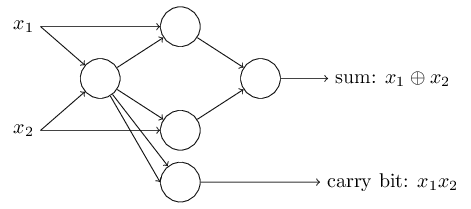
Can we implement XOR gate in a single neuron?

Before answer to this question let's ask a few more!

whats best architecture for our data?

Decision boundary

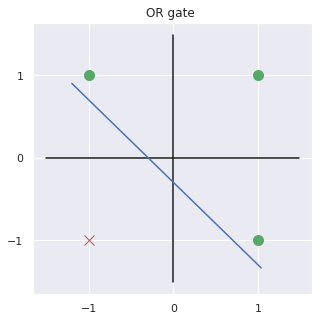
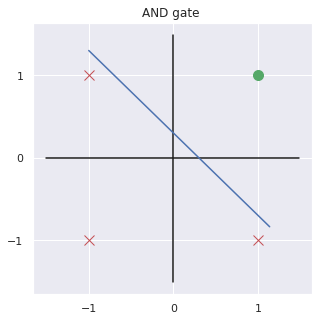
Decision boundary

 Regression vs single neuron

y = ax+b
  • Linear regression
  • Single neuron
y = w_0 x + b_0

Regression vs single neuron

P(y=1|x) = \sigma( \frac{1}{1+e^{-(a_1x_1+a_2x_2+b)}})
  • Logistic regression
  • Single neuron
P(y=1|x) = \sigma( \frac{1}{1+e^{-(w^TX+b)}})

 Logistic Regression vs single neuron

A neural network is made up of multiple logistic regressions

Summary

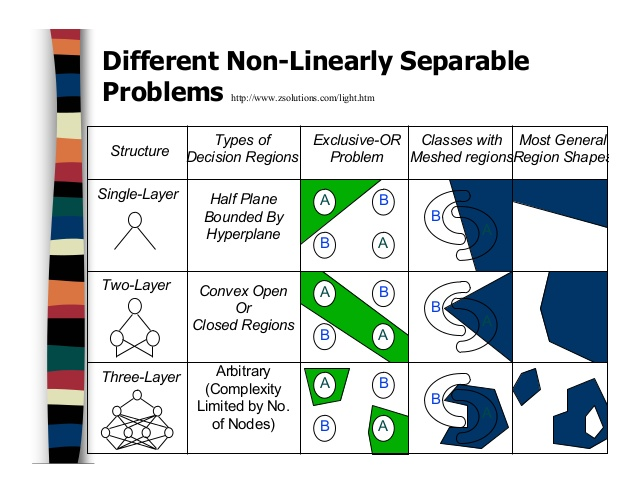
  • Artificial Neural Networks are NON Linear classifiers
  • Output of a single neuron is weighted sum affined by a non linear function
  • More neurons means more complex decision boundries

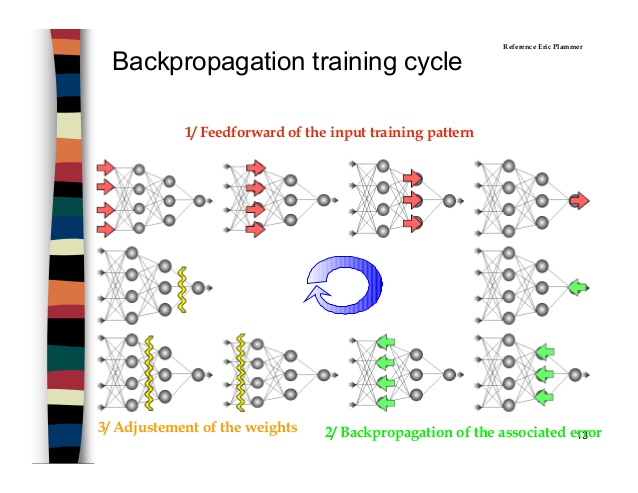
BACKPROPAGATION  Algorithm

unfortunately it's time to

DIVE INTO MATHEMATICS 

In this section  we focus on Supervised Learning to train our neural network

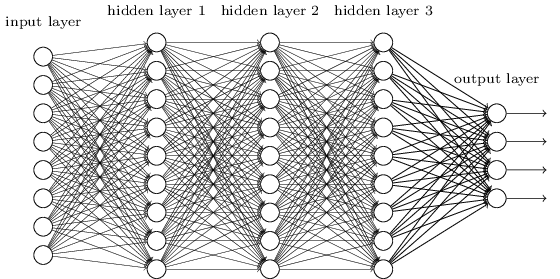
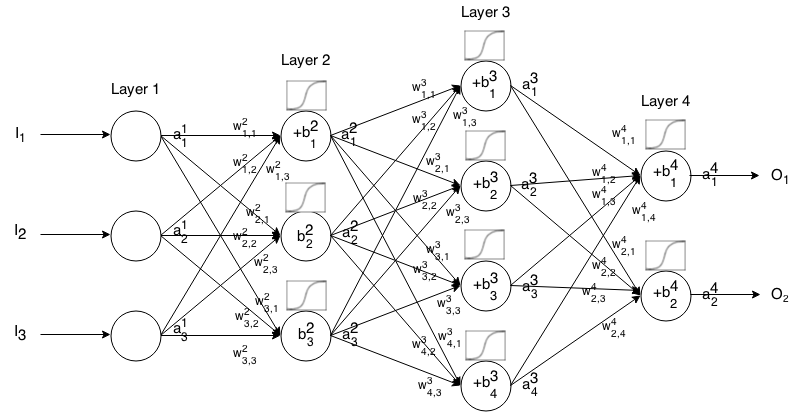
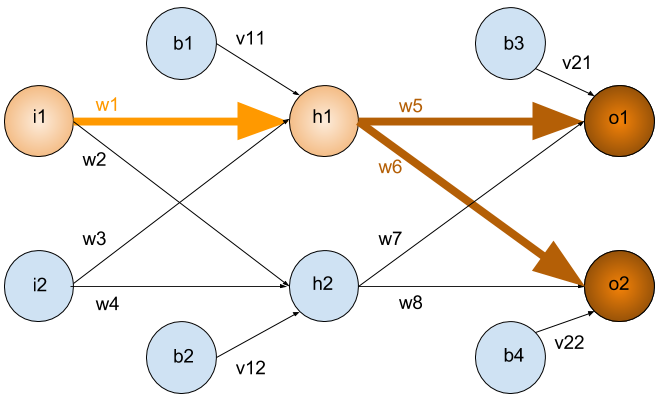
General Structure

We split our network to 3 main layers

  • Input layer
  • Hidden layers
  • Output layer

General Structure

This type of Artificial neural network known as MultiLayer Perceptron (MLP)

Since there is no cycle in this architecture we call this Feed Forward Network

Now can you guess why we shouldn't use linear activation function?

Lets start with an example

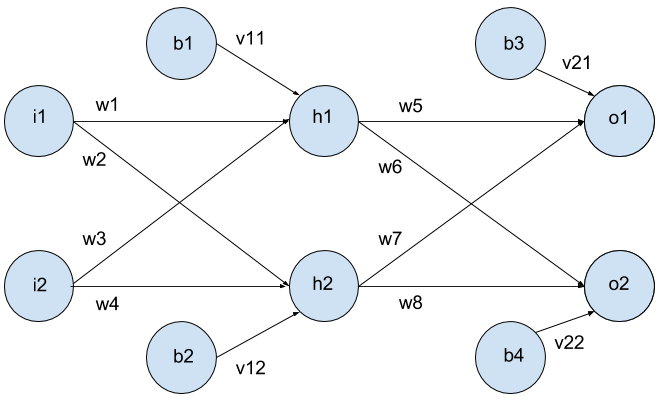
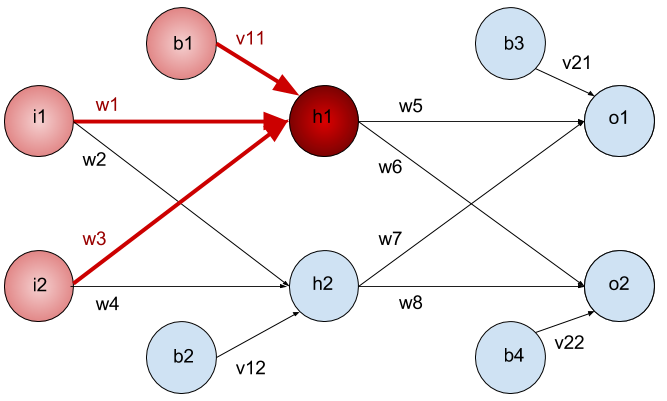
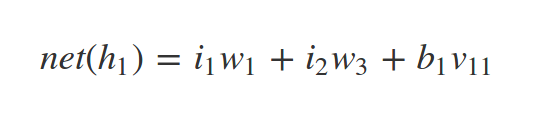
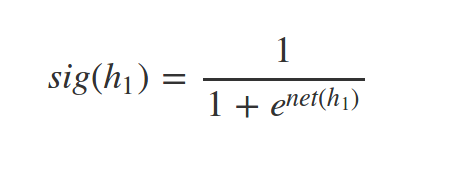
Whats \(net(h_2)\) and \(sig(h_2)\) ?

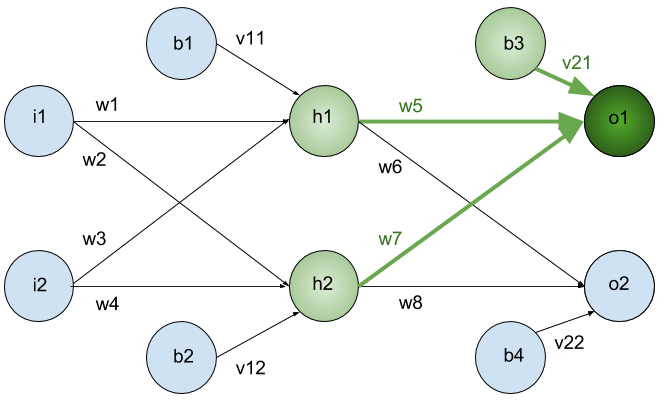
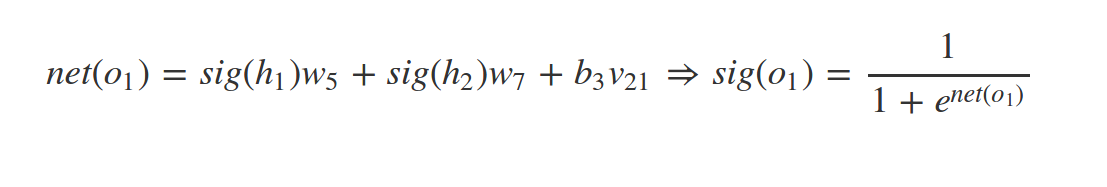
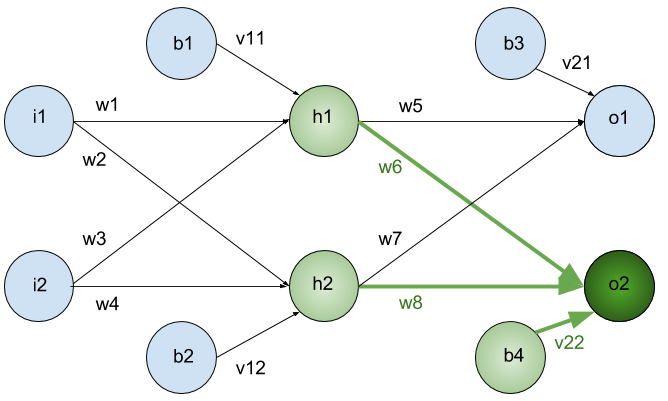
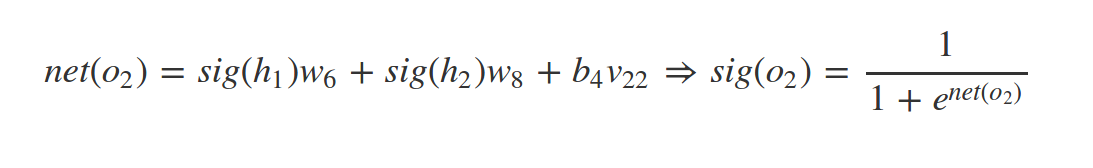
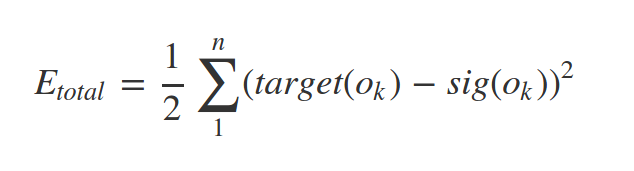
since we have target value of our samples (supervised learning) we can find the error of network predict as follow:

some times this called loss function

Where n = number of neurons at output layer

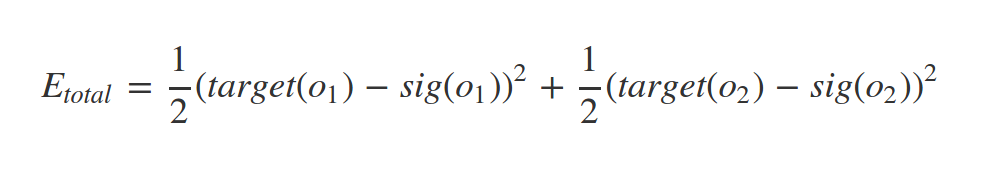
In our example:

In order to get best predicts we need to minimize error value

To minimize error we can:

  • change bias
  • change weights
  • change previous activations!

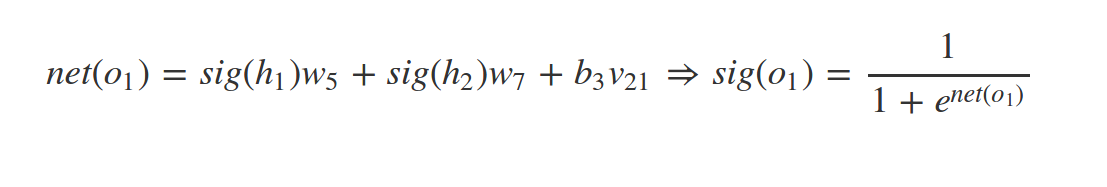
since

As you saw this lost function has a quadratic form

It's obvious that this function may has much many variables

so we cant use calculus to find the minimum!

Learning algorithms

  • Levenberg marquardt
  • Quasi newton
  • Evolutionary methods
  • Gene expression programming
  • . . .
  • . . .
  • Gradient descent
    • Adam
    • BFGS
    • RMSProp
    • . . .
  • Newton's method
  • Conjugate gradient

Learning algorithms

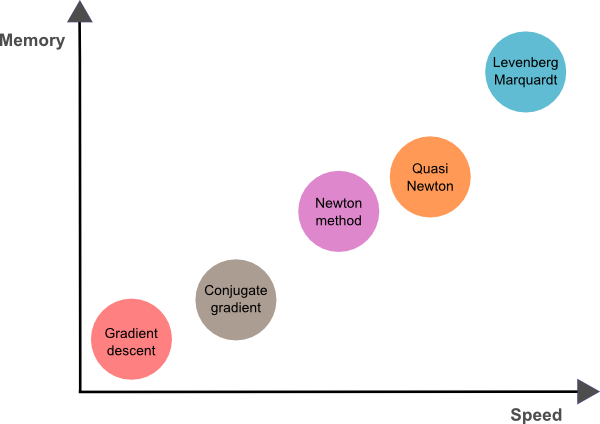
Here we focus on Gradient descent algorithm

Let's forget neural network aspects of this function

 

Just think you have a n-variable quadratic function and we want to minimize it

C:ℝ^n \longrightarrow ℝ

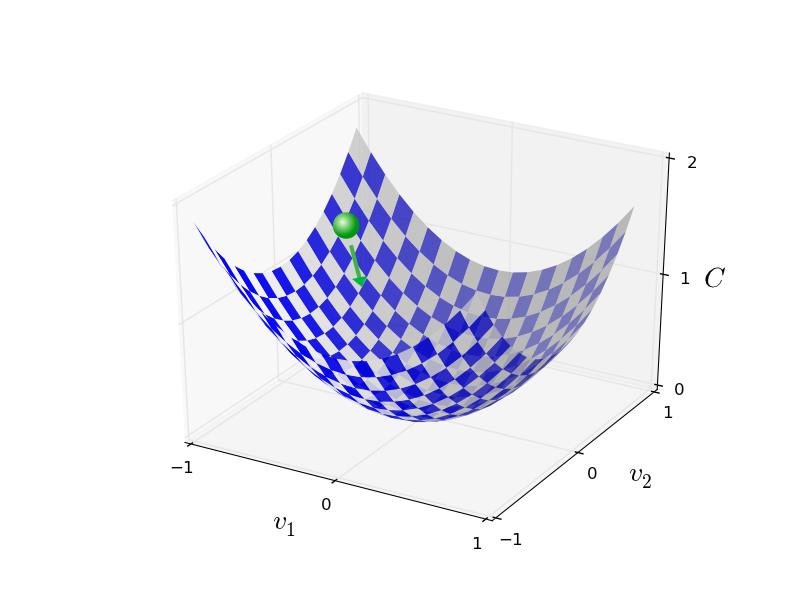
we simulate the random ball's rolling down motion by computing derivatives of function

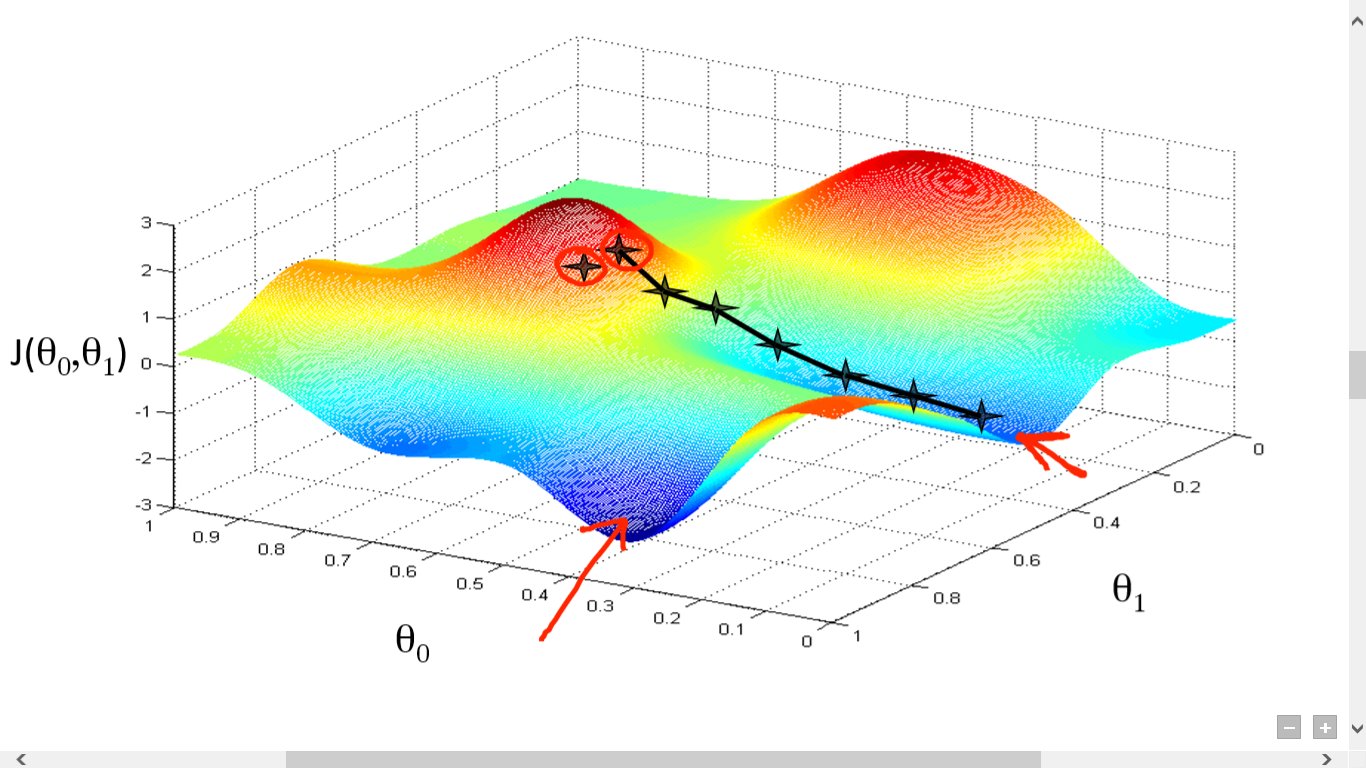
  • Calculate slope at current position
  • Updates parameters in opposite direction of gradient
\Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2

Since

we are going to find a way to make \(\Delta C\) negative

Define:

\Delta v \equiv \left(\begin{array}{c} \Delta v_1 \\ \Delta v_2 \end{array}\right)
\nabla C \equiv \left( \frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2} \right)

So:

\Delta C \approx \nabla C \cdot \Delta v

we want to make \(\Delta C\) negative since we look for a good \(\Delta v\)

let's suppose   \(\Delta v =  -\eta \nabla C^T\)

we had    \(\Delta C \approx \nabla C \cdot \Delta v \)    so:

\Delta C \approx -\eta \nabla C \cdot \nabla C^T = -\eta \|\nabla C\|^2

Obviously \(\Delta C \lt 0\)

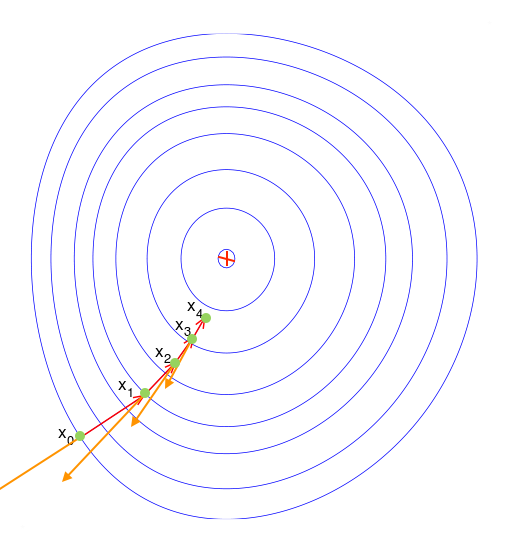
GOAL:

find \(\Delta v\) to change ball position in order to rich the functions minimum

v \rightarrow v' = v -\eta \nabla C.
v \rightarrow v' = v + \Delta v

if we do this over and over we rich global minimum

This approach works with more than two variable

gradient descent in neural network form

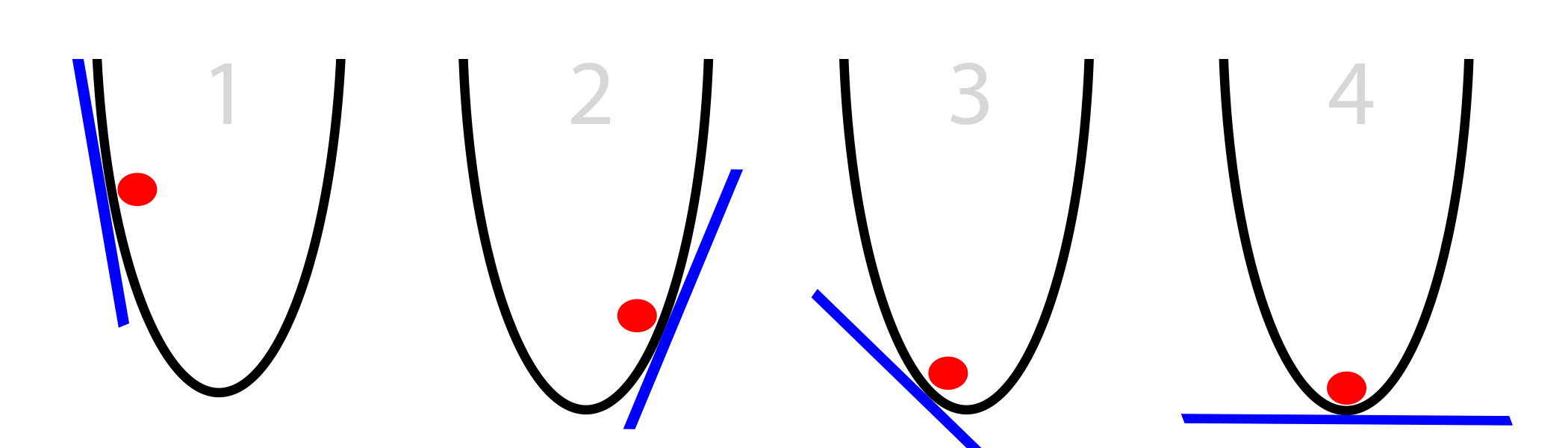
w_k \rightarrow w_k' = w_k-\eta \frac{\partial C}{\partial w_k}
b_l \rightarrow b_l' = b_l-\eta \frac{\partial C}{\partial b_l}
  • Batch gradient descent
  • Mini-Batch gradient descent
  • Stochastic gradient descent

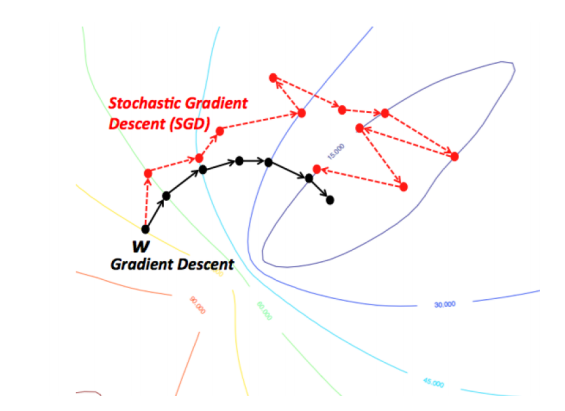
Gradient descent variants

Computes gradient with the entire dataset

  • Pros:
    • Guaranteed to converge to global/local minimum for convex/non-convex error surfaces
  • Cons:
    • Intractable for datasets that do not fit in memory
    • Very slow

Batch gradient descent

Performs update for every mini-batch of n examples

  • Pros
    • Reduces variance of updates
    • Can exploit matrix multiplication primitives
  • Cons
    • Mini-batch size is a hyperparameter

Mini-batch gradient descent

Same as Mini-batch but unit batch size on shuffled data

  • Pros
    • Much faster than batch gradient descent
    • Allows online learning
  • Cons
    • High variance updates.

Stochastic gradient descent

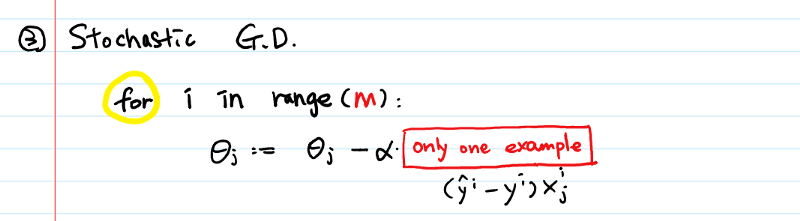
BGD vs SGD

How to find \(\nabla C\)?

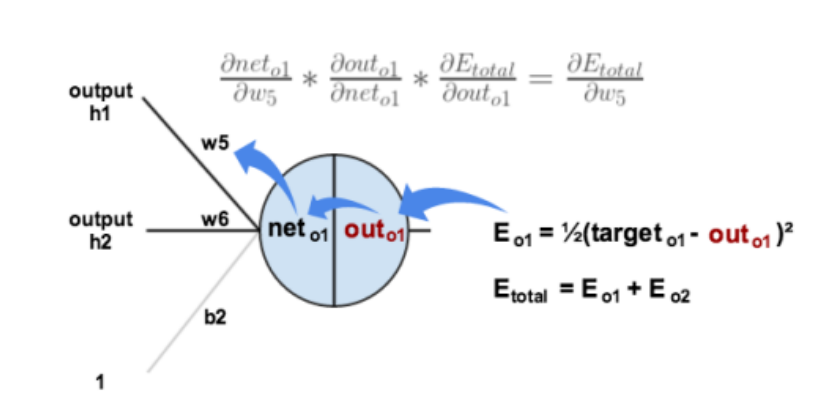
Backpropagation

Let's see an example

u' = n\ u'\ u^{n-1}
\begin{aligned} \dfrac{d}{dx} \sigma(x) &= \dfrac{d}{dx} \left[ \dfrac{1}{1 + e^{-x}} \right] \\ &= \dfrac{d}{dx} \left( 1 + \mathrm{e}^{-x} \right)^{-1} \\ &= -(1 + e^{-x})^{-2}(-e^{-x}) \\ &= \dfrac{e^{-x}}{\left(1 + e^{-x}\right)^2} \\ &= \dfrac{1}{1 + e^{-x}\ } \cdot \dfrac{e^{-x}}{1 + e^{-x}} \\ &= \dfrac{1}{1 + e^{-x}\ } \cdot \dfrac{(e^{-x}+ 1) - 1}{1 + e^{-x}} \\ &= \dfrac{1}{1 + e^{-x}\ } \cdot \left( \dfrac{1 + e^{-x}}{1 + e^{-x}} - \dfrac{1}{1 + e^{-x}} \right) \\ &= \dfrac{1}{1 + e^{-x}\ } \cdot \left( 1 - \dfrac{1}{1 + e^{-x}} \right) \\ &= \sigma(x) \cdot (1 - \sigma(x)) \end{aligned}

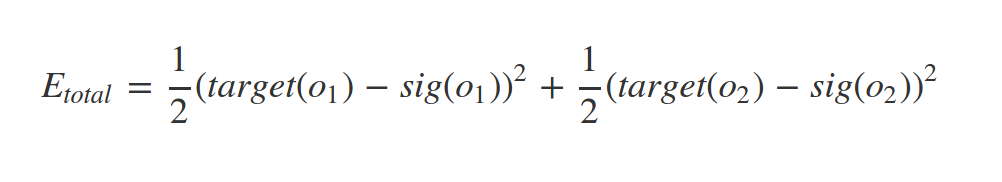
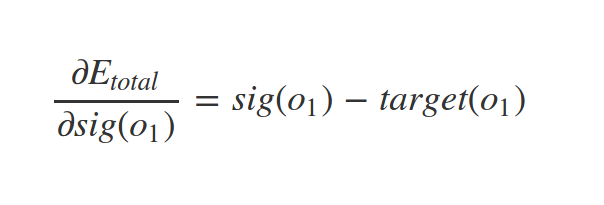
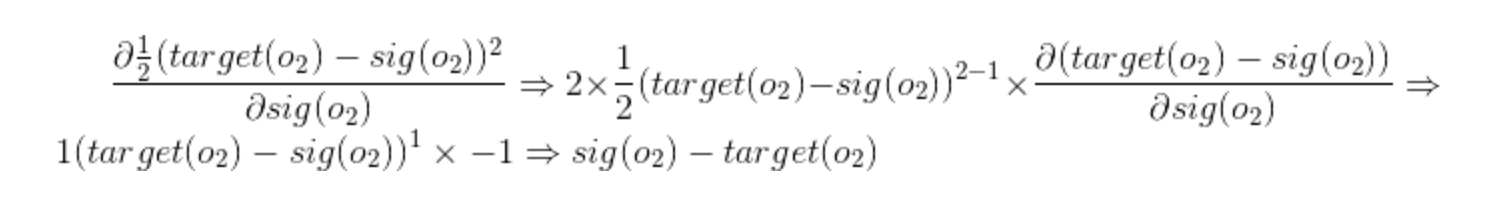
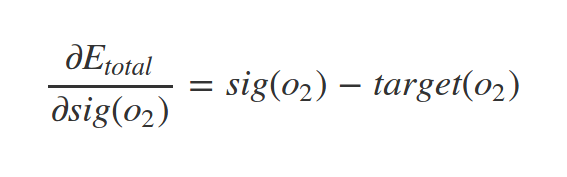
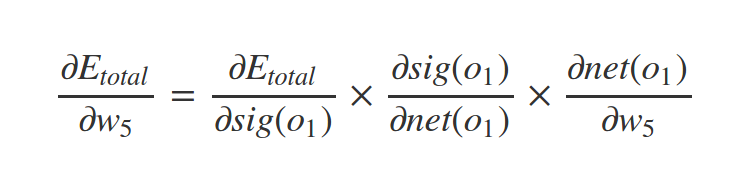
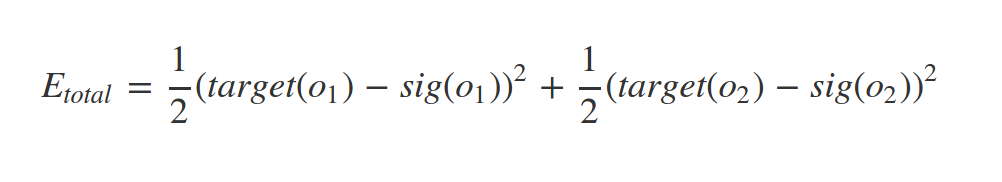
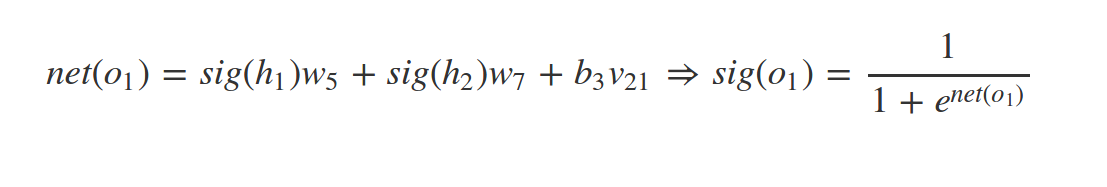
Derivative of sigmoid

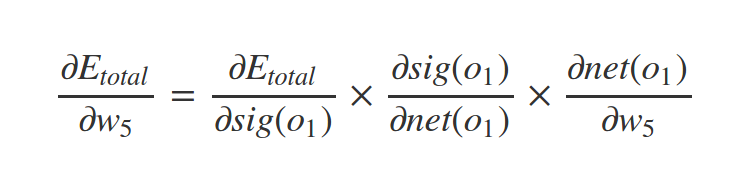
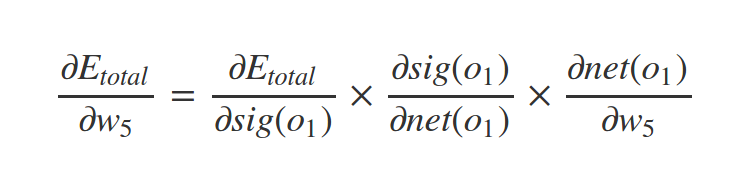
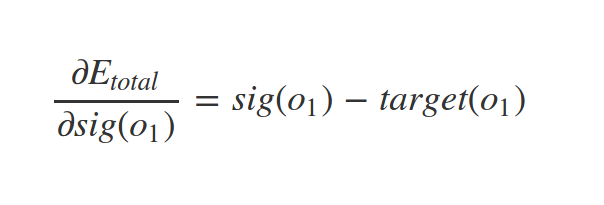
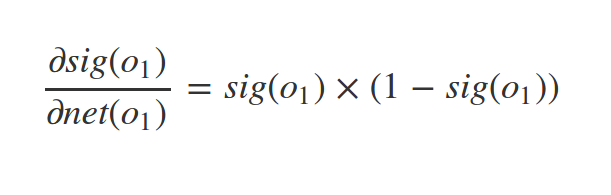
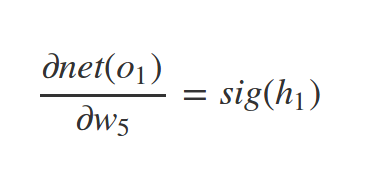
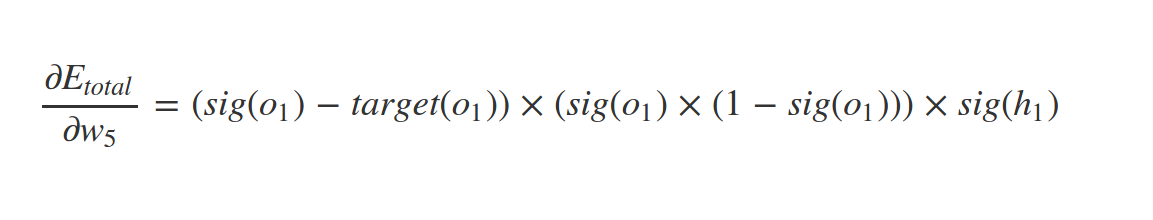
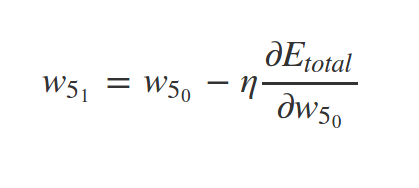
Similarly  we have:

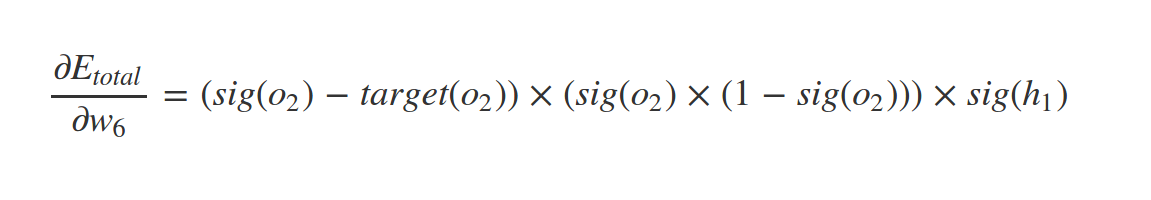
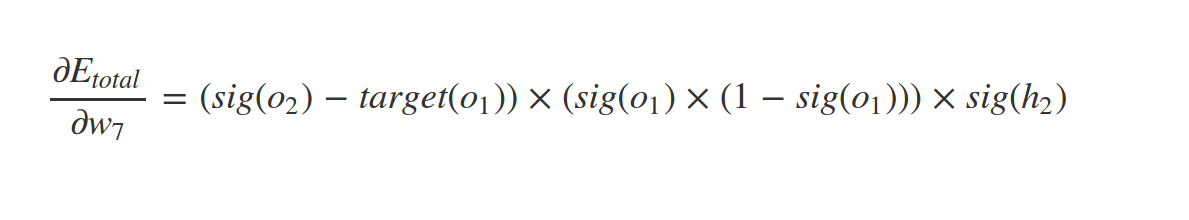
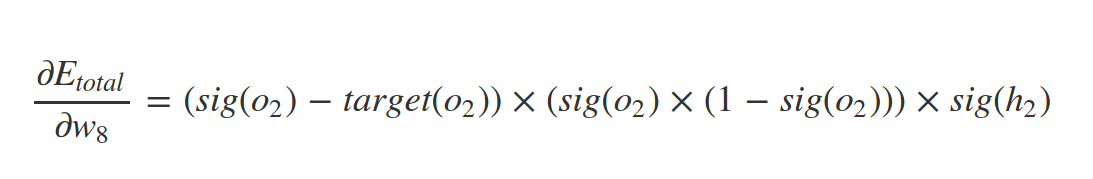
What about \(w_1\) ?

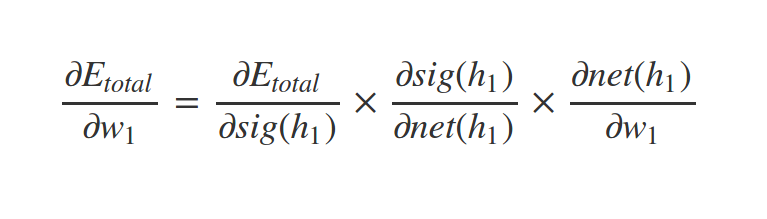
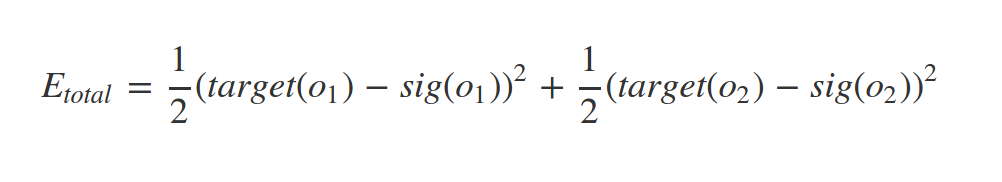
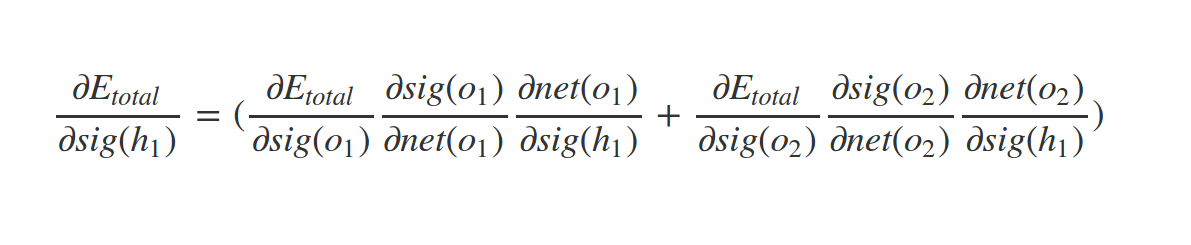
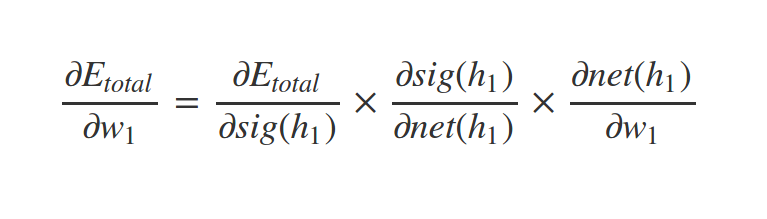
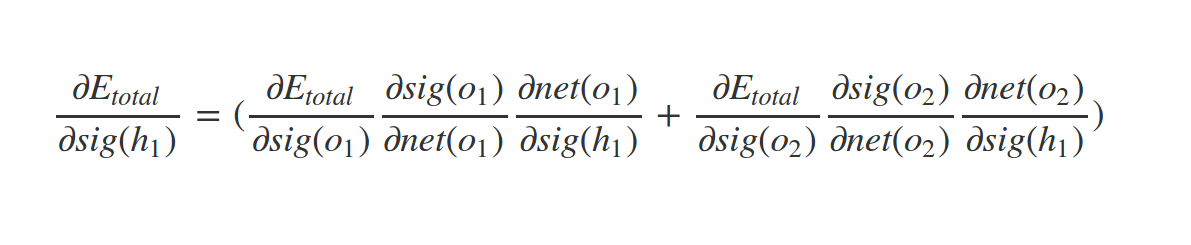
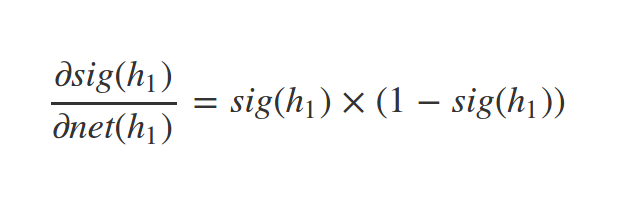
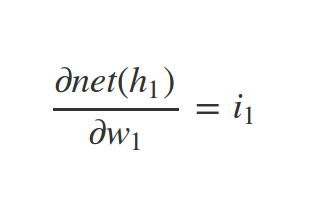
Similarly

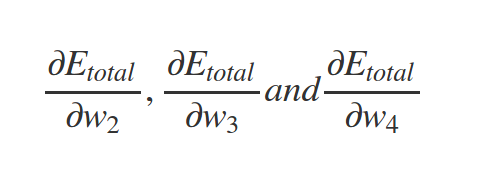
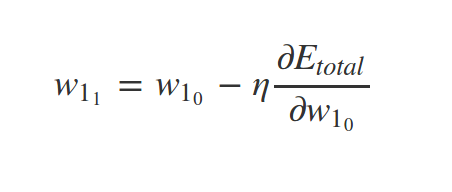
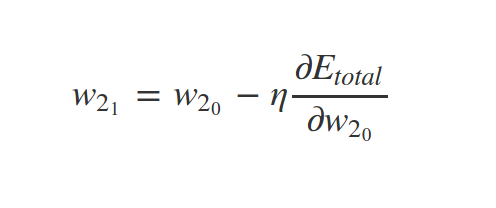
And so on . . .

What about biases?

Now you know why we need an activation function with big gradient for all inputs!

Why \(\eta\) ?

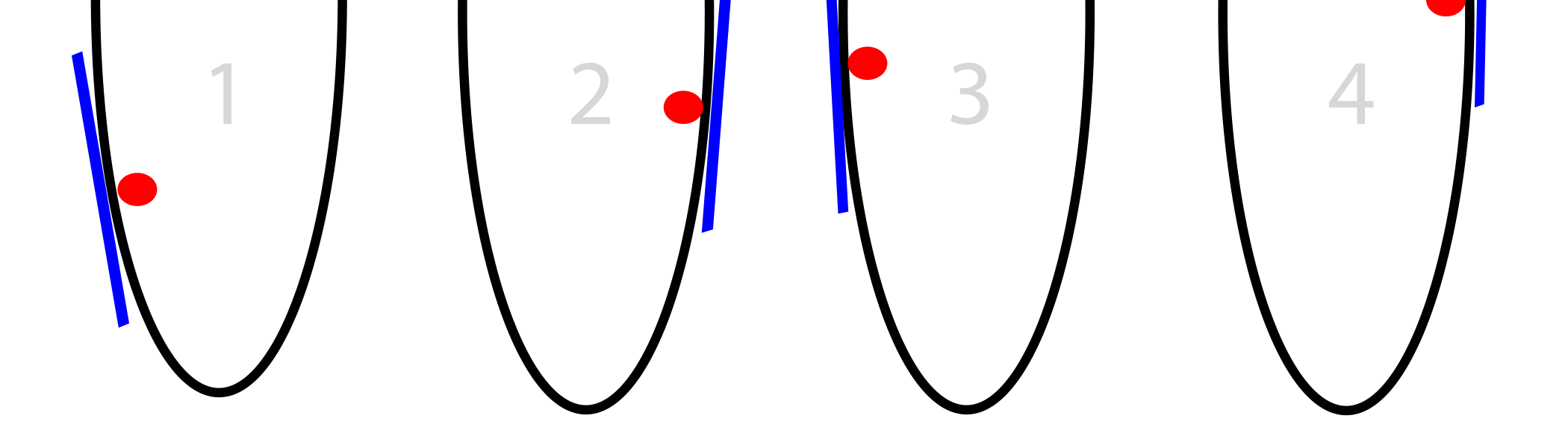
Local minimum and gradient descent!

http://iamtrask.github.io/2015/07/27/python-network-part2/

Summary

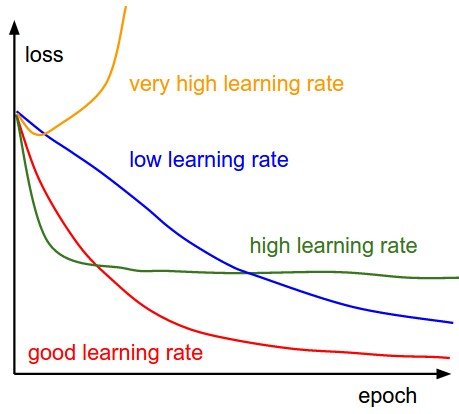
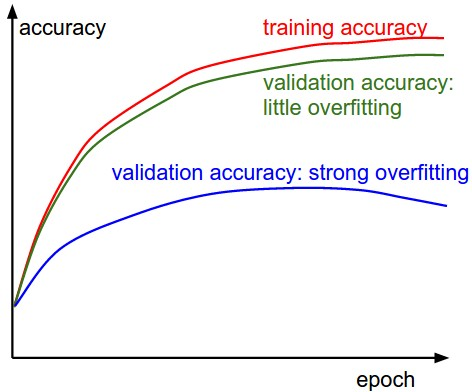
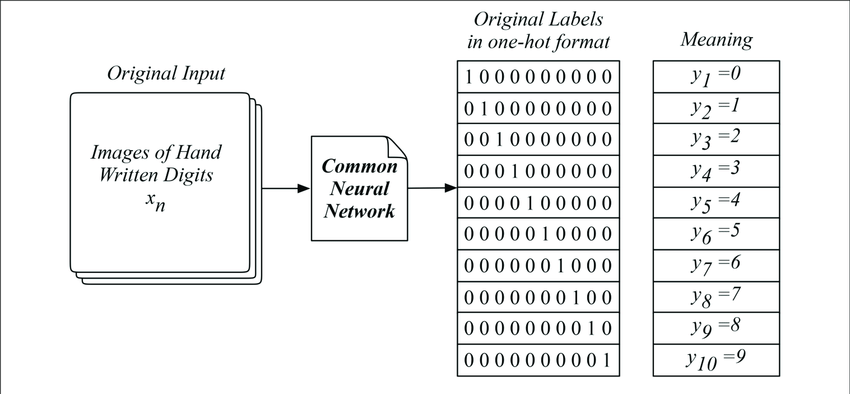
Data encoding

Categorical or Nominal data

Many machine learning algorithms cannot operate on label data

Data encoding

One-hot encoding

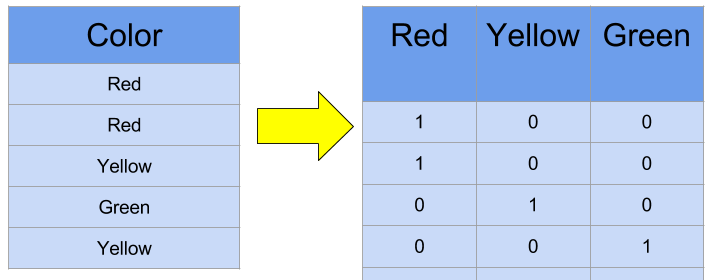
Softmax

Theorem.

2 layer MLP is a universal approximator

Link to image

CNN

datasets: train,test,valid

over-fit, vs under-fit -> regulaization

 

fully connected-layer, dense

https://stats.stackexchange.com/questions/297749/how-meaningful-is-the-connection-between-mle-and-cross-entropy-in-deep-learning

 

https://stats.stackexchange.com/questions/167787/cross-entropy-cost-function-in-neural-network

 

https://datascience.stackexchange.com/questions/9302/the-cross-entropy-error-function-in-neural-networks

 

https://www.quora.com/What-are-the-differences-between-maximum-likelihood-and-cross-entropy-as-a-loss-function

 

https://aboveintelligent.com/deep-learning-basics-the-score-function-cross-entropy-d6cc20c9f972

https://en.wikipedia.org/wiki/Perceptron

 

delta rule,hebb,backpropagation,feed forward

 

https://medium.com/biffures/all-the-single-neurons-14de29a40f47

 

https://towardsdatascience.com/logistic-regression-detailed-overview-46c4da4303bc

 

https://en.wikipedia.org/wiki/Backpropagation

 

https://ml4a.github.io/ml4a/how_neural_networks_are_trained/

 

https://www.slideshare.net/MohdArafatShaikh/artificial-neural-network-80825958

 

https://juxt.pro/blog/posts/neural-maths.html

http://www.robertsdionne.com/bouncingball/

softmax probability vs sigmoid

 

References

  • Fausett, L.V. and Fausett, L., Fundamentals of Neural Networks: Architectures, Algorithms, and Applications, 1994

  • KIYOSHI KAWAGUCHI, BSEE , A MULTITHREADED SOFTWARE MODEL FOR BACKPROPAGATION NEURAL NETWORK APPLICATIONS, 2000

  • en.wikipedia.org/wiki/Neuron
  • slideshare.net/neurosciust/what-is-a-neuron
  • slideshare.net/HumaShafique/neuron-structure-and-function
  • www2.fiit.stuba.sk/~kvasnicka/Seminar_of_AI/Benuskova_synplast.pdf
  • slideshare.net/MohdArafatShaikh/artificial-neural-network-80825958
  • https://towardsdatascience.com/activation-functions-and-its-types-which-is-better-a9a5310cc8f
  • https://datascience.stackexchange.com/questions/26475/why-is-relu-used-as-an-activation-function
  • https://medium.com/data-science-bootcamp/understand-the-softmax-function-in-minutes-f3a59641e86d
  • http://www.themenyouwanttobe.com/data-science-resources/
  • https://towardsdatascience.com/difference-between-batch-gradient-descent-and-stochastic-gradient-descent-1187f1291aa1
Made with Slides.com