On the Stability of tight Planetary Systems
Almog Yalinewich
Cristobal Petrovich
1.8.19
Motivation
Oligarchic Growth

Isolation mass
M_i \approx \frac{\left(\Sigma a^2\right)^{3/2}}{M_s^{1/2}}
\approx 1 M_{☽}
Implications of Survival Times
Too short
Too long
Habitability


\Delta a



Numerical Experiments
Evolution of the Instability
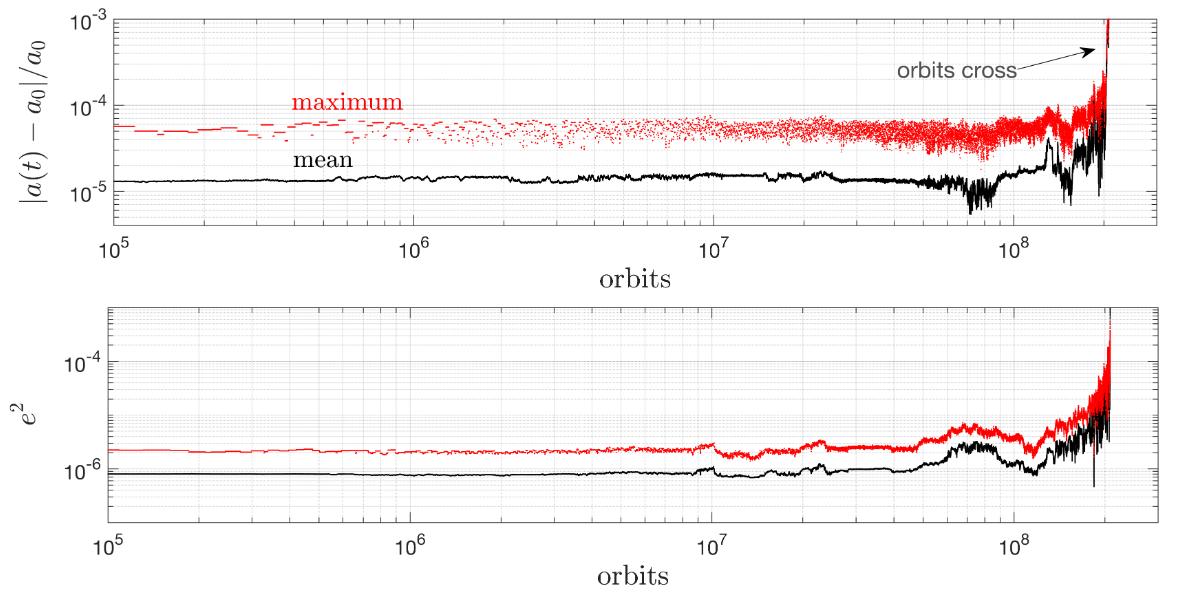
Evolution of the Instability
Previous Analytic Approaches
Chaotic Diffusion
Impulse Approximation
v
\delta v_{\perp}
b
\delta v_{\perp} \approx \frac{G m}{b v}
m
Adaptation to the Planetary Scattering
\sqrt{\frac{G M}{a}} \frac{\Delta a}{a}
\Delta a
a
\Delta v_{\perp} \approx \frac{G m}{b v}
v \approx \sqrt{\frac{G M}{a}} \frac{\Delta a}{a}
\delta v_{\perp} \approx \frac{G m}{\Delta a^2} \sqrt{\frac{a^3}{G M}}
\delta v_{\theta} \approx e \frac{G m}{\Delta a^2} \sqrt{\frac{a^3}{G M}}
Diffusion Time
t_s \approx \sqrt{\frac{a^3}{G M}} \frac{a}{\Delta a}
\delta e^2 \approx \frac{\delta j}{j} \approx \delta v_{\theta} / \sqrt{\frac{G M}{a}} \Rightarrow \delta e \approx \frac{m}{M} \frac{a^2}{\Delta a^2}
e_f \approx \frac{\Delta a}{a}
T \approx t_s \left(\frac{e_f}{\delta e}\right)^2 \approx \sqrt{\frac{a^3}{G M}} \left(\frac{\Delta a}{a}\right)^5 \left(\frac{M}{m}\right)^2
Not steep enough
Higher order interaction gives
T \propto \left(\Delta a/a\right)^8
Why doesn't it work?
Angles are not random

Ellipse anti - alignment
Periapse Drift
\delta v_{r} \approx \frac{G m}{\Delta a^2} \sqrt{\frac{a^3}{G M}}
Energy / Angular momentum unchanged, but the position of periapse does change
\vec{e} = \frac{\vec{v} \times \vec{j}}{G M} - \hat{r}
\psi
\psi \approx \pm \frac{m}{M} \frac{a^2}{\Delta a^2}
Our Work
Hamiltonian Perturbation Theory
H = H_0 \left( \vec{I}\right) + \varepsilon H_1 \left(\vec{I}, \vec{\varphi} \right)
H_1 = \sum_{\vec{k}} h_{\vec{k}} \left(\vec{I} \right) \exp \left(i \vec{k} \cdot \vec{\varphi}\right)
\varepsilon=0 \Rightarrow \vec{I} = {\rm const}, \vec{\varphi} = \vec{\varphi}_i+\vec{\omega} t, \vec{\omega}= \frac{\partial H_0}{\partial \vec{I}}
First order expansion
\vec{I}_1 = \varepsilon \sum_{\vec{k}} h_{\vec{k}} \left(\vec{I}\right) \frac{\exp \left(i \vec{k} \cdot \vec{\varphi}\right)}{\vec{k} \cdot \vec{\omega} }
Resonance
\omega x
\dot{x}
For the harmonic oscillator
\vec{k} \cdot \vec{\omega} = 0
\vec{k} \cdot \vec{\omega} \neq 0
\omega x
\dot{x}
\omega x
\dot{x}
Dirichlet Approximation Theorem
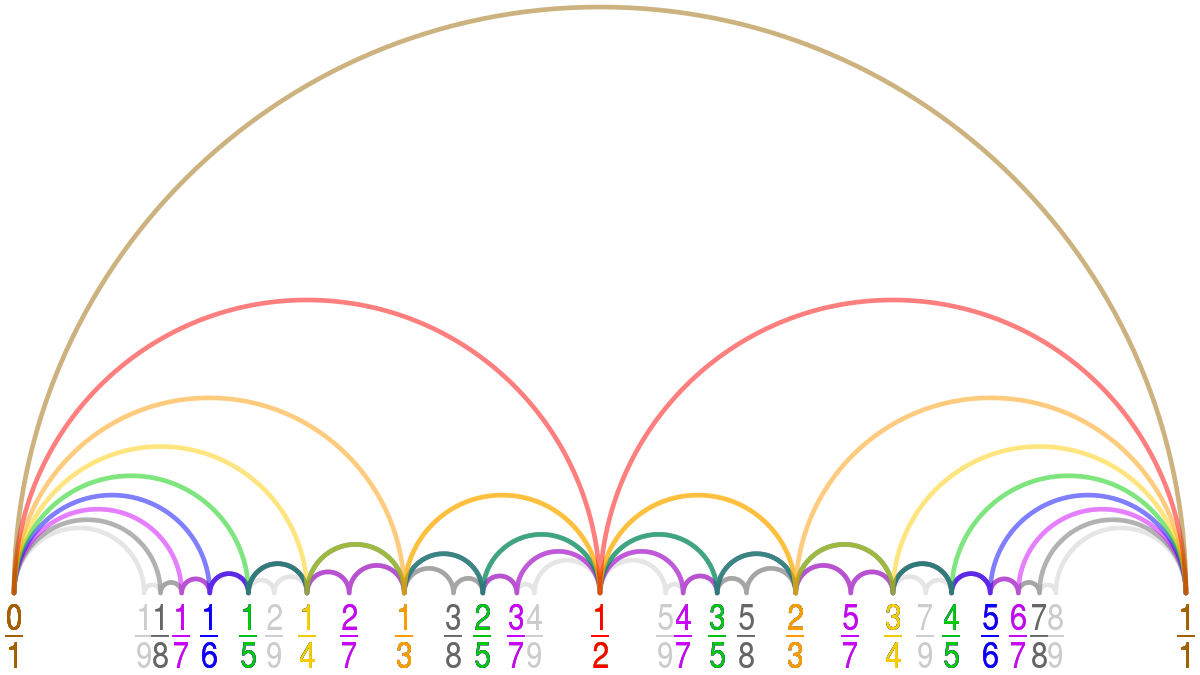
\min_{p,q} \left|\alpha - \frac{p}{q} \right| < Q^{-2}
q < Q;Q,p,q\in \mathbb{N};\alpha \in \mathbb{R}
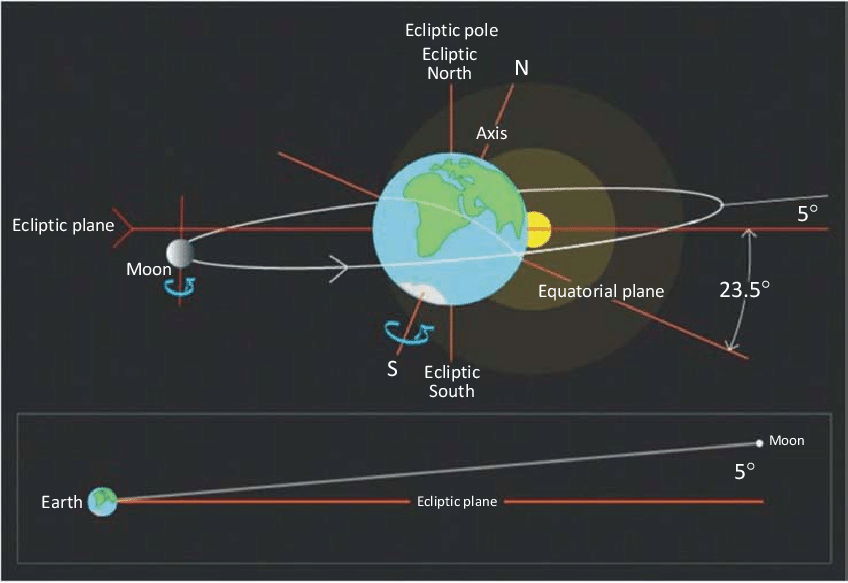
Synodic month 29.53 days
Nodical month 27.21days
(actually half)
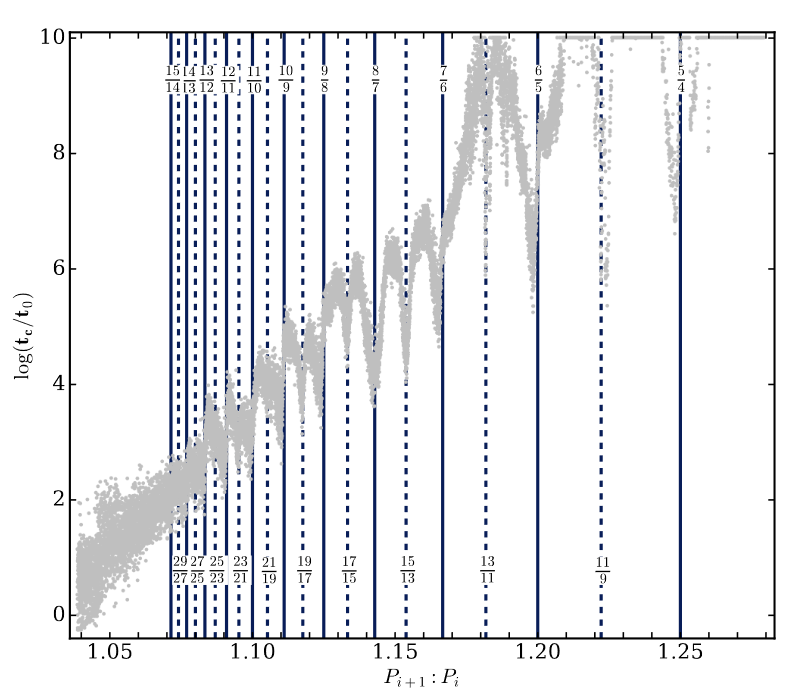
Period ratio 2.15
\approx \frac{13}{6}, \frac{89}{41}, \frac{484}{223}


Degrees of Freedom
\min_{\vec{k}} \left|\vec{k} \cdot \vec{\omega} \right| = \min_{\vec{k}} \left|\sum_{i=1}^N k_i \omega_i\right| = \omega_N \left| \sum_{i=1}^{N-1} k_i \frac{\omega_i}{\omega_N} - k_N \right| < |k|^{N-1}
\left|k \right| = \sum_i \left|k_i \right|
Paley Wiener Theorem
H_1 \propto \frac{1}{\sqrt{r_1^2 + r_2^2 - 2 r_1 r_2 \cos \theta}} \propto \sum_j b_{\frac{1}{2}}^j \left(\frac{r_2}{r_1}\right) \cos \left(j \theta\right)
b_{\frac{1}{2}}^j \left(\alpha\right) = \frac{1}{\pi} \int_0^{2 \pi} \frac{\cos \left(j \theta\right)d\theta}{\sqrt{1 - 2 \alpha \cos \theta + \alpha^2}}
b_{\frac{1}{2}}^j \left(\alpha\right) \propto \exp \left(-\left(\alpha-1\right) |j|\right) \approx \exp \left(-\frac{\Delta a}{a} |j|\right)
Nekhoroshev Theorem
\left|I \left(t\right) - I \left(0\right) \right| < C_1 \varepsilon^{1/2N}
A Hamiltonian system is bounded by
For a time
t < T = C_2 \exp \left(C_3 / \varepsilon^{1/2N} \right)
...while not eternity, this is a considerable slice of it
Adaptation to Planetary Systems
Dynamics dominated by three body resonances
# dof = 3*2 angles - 2 integrals of motion = 4
Small parameter
\varepsilon = \left(m/M\right)^2
Energy and rotation angle
T \approx C_2 \exp \left(C_3 \varepsilon^{-1/2N}\right)
T \approx C_2 \exp \left(C_3 \varepsilon^{-1/8}\right)
T \approx C_2 \exp \left(C_3 \left(\frac{m^2}{M^2}\right)^{-1/8}\right)
T \approx C_2 \exp \left(C_3 \left(\frac{M}{m}\right)^{1/4}\right)
Paley Wiener
Sinodic Time
T \approx C_2 \exp \left(c_3 \frac{\Delta a}{a} \left(\frac{M}{m}\right)^{1/4}\right)
T \approx c_2 \sqrt{\frac{a^3}{G M}} \frac{a}{\Delta a} \exp \left(c_3 \frac{\Delta a}{a} \left(\frac{M}{m}\right)^{1/4}\right)
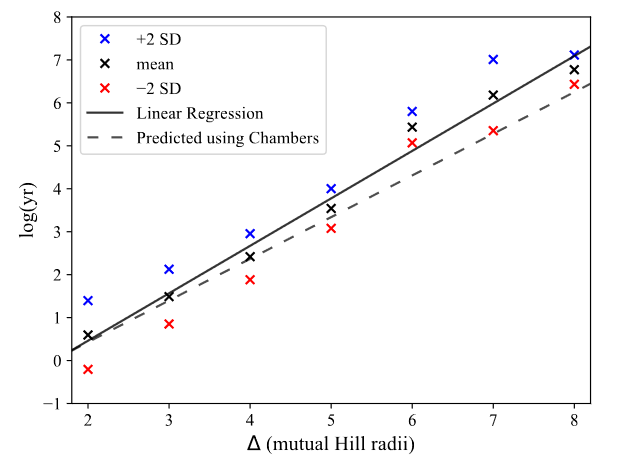
Comparison to Simulations
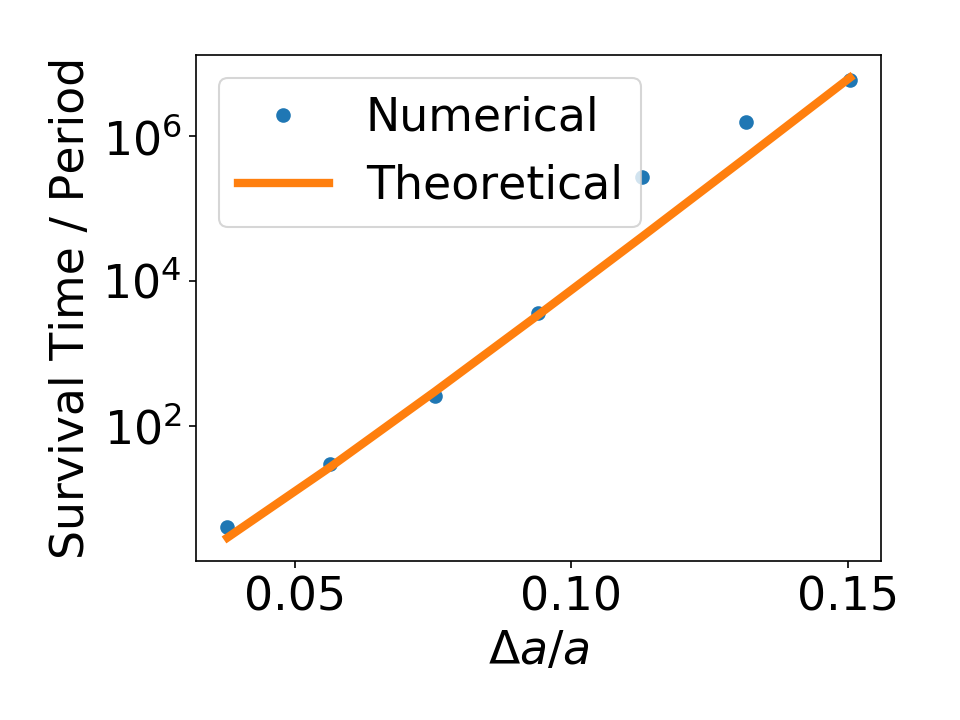
T/P \approx 5 \times 10^{-4} \cdot \left( \frac{a}{\Delta a}\right) \exp \left(8 \left(\frac{\Delta a}{a}\right) \left(\frac{M}{m}\right)^{1/4}\right)
Outlook