Measuring the Black Hole Spin with Optical Vortices
Almog Yalinewich
16.5.2019
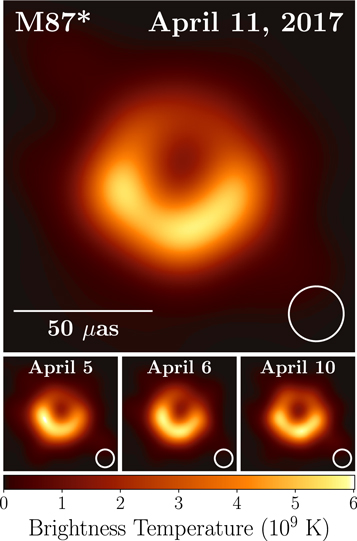
EHT Image
Mass is straightforward
Spin?
Simulations and Jets
Simulations and Jets
wanted: cleaner measurement
Phase Information




Phase Retrieval




\frac{\partial I}{\partial z} = -\frac{1}{2 \pi} \nabla_{x,y} \left(I \nabla_{x,y} P\right)
\frac{\partial P}{\partial z} = \frac{1}{4 \pi \sqrt{I}} \nabla_{x,y}^2 \sqrt{I} - |\nabla_{x,y} P|^2
\psi = \sqrt{I} \exp \left(i P\right)
Phase Map

Magnetic Faraday Effect


Mathematical Model
Paraxial Approximation
\frac{1}{c^2} \frac{\partial^2 \psi}{\partial t^2} - \nabla^2\psi = 0
Wave equation
monochromatic wave
Helmholtz equation
\left(k^2 +\nabla^2\right) \psi = 0
propagation primarily along z direction
\left(\nabla_{\perp}^2 + i k \frac{\partial}{\partial z}\right) \psi = 0
Paraxial equation
Gaussian Modes
\left(\nabla_{\perp}^2 + i k \frac{\partial}{\partial z}\right) \psi = 0
Looks like the diffusion equation
Self similar solutions are Gaussian
\psi \propto \frac{w_0}{w\left(z\right)} \exp \left(-\frac{r^2}{w^2\left(z\right)}\right) \exp \left(-i \left(kz+\frac{k r^2}{2R\left(z\right)} - \psi \left(z\right)\right)\right)
w \left(z\right) = w_0 \sqrt{1+\frac{z^2}{z_R^2}}
z_R = k w_0^2
R \left(z\right) = z \left(1+\frac{z_R^2}{z^2}\right)
\psi = \arctan \left(z/z_R\right)
Gauss Laguerre Modes
\left(\frac{\partial^2}{\partial r^2} + \frac{1}{r} \frac{\partial}{\partial r} - \frac{m^2}{r^2} + i k \frac{\partial}{\partial z}\right) \psi = 0
Polar coordinates
Self similar solutions
\psi \propto \frac{w_0}{w\left(z\right)} \exp \left(-\frac{r^2}{w^2\left(z\right)}\right) \left(\frac{\sqrt{2} r}{w \left(z\right)} \right)^{|m|} L_p^{|m|} \left(\frac{2 r^2}{w^2 \left(z\right)}\right) \times
\times \exp \left(-i \left(kz+\frac{k r^2}{2R\left(z\right)} - \psi \left(z\right) - m \theta \right)\right)
Optical Vortex
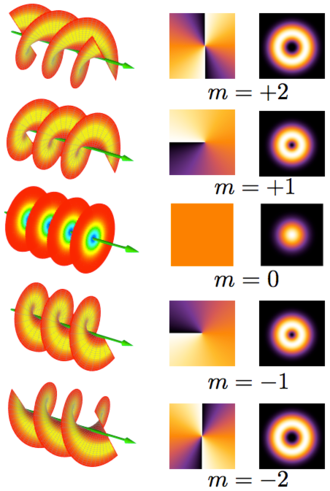
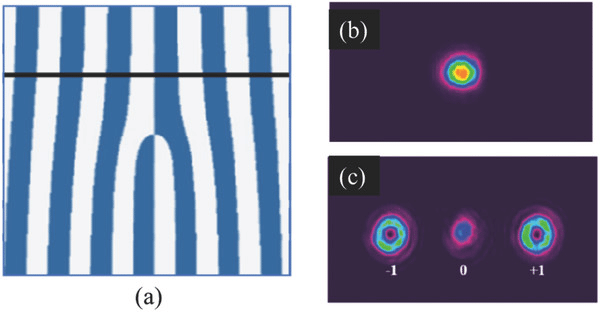
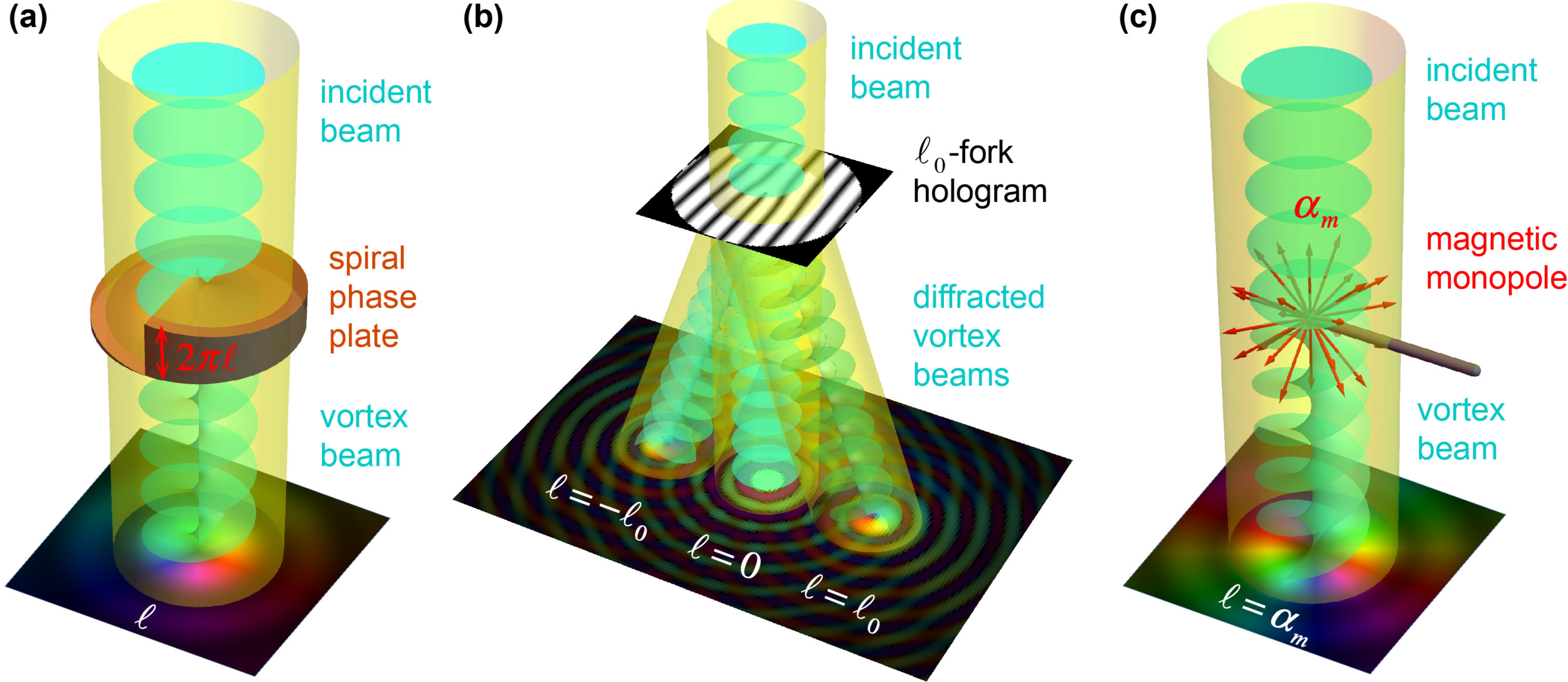
Polarisation
Results
Observations
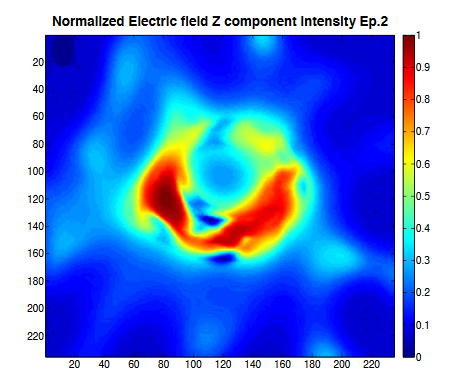
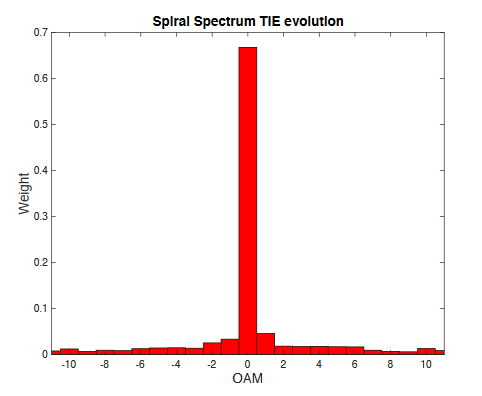
Laguerre Gauss modes => Spiral Spectrum
Simulation
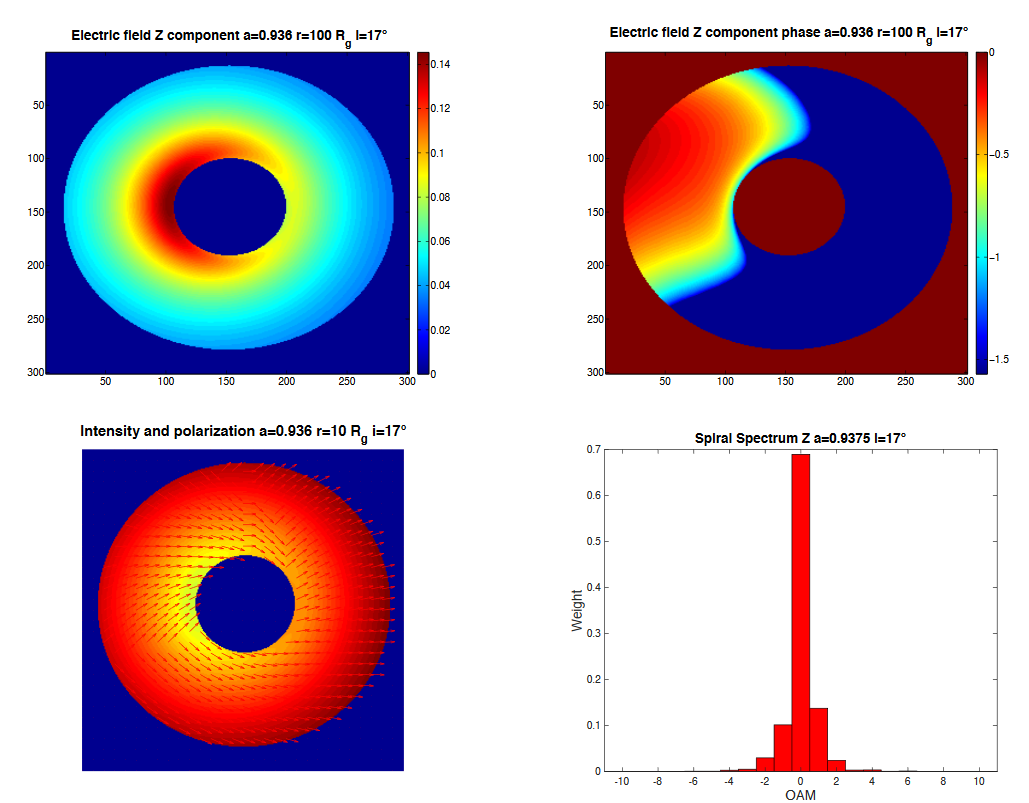
Bottom Line
a = 0.9 \pm 0.1




