Black widow evolution:magnetic braking by an ablated wind
Almog
Yalinewich
Pulsar
Coffee
7.2.20
Mass Loss from a Black Widow

Energy budget
Efficiency?
Albedo?
(regressive energy distribution)
Extremely Low Mass Companion
PSR J1719-1438 and PSR J2322-2650


Parker Wind

Sonic Point
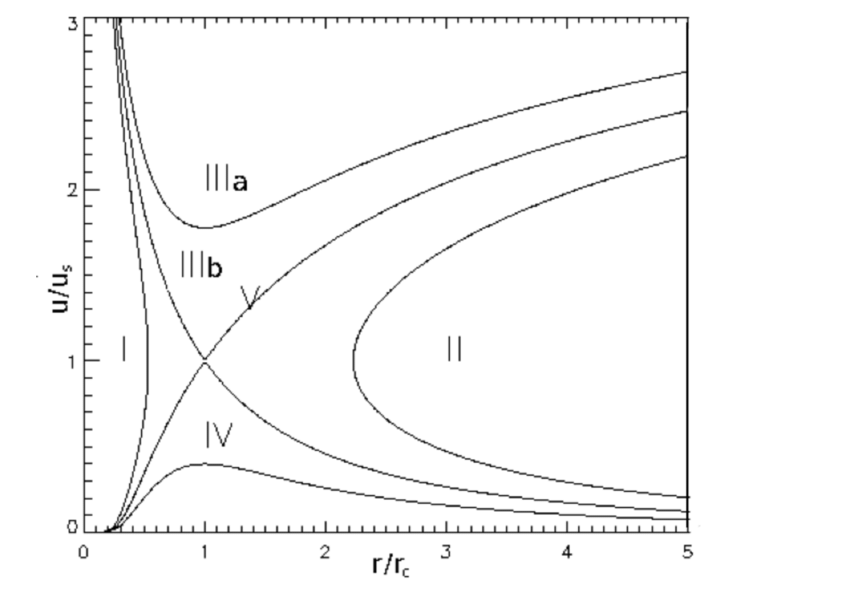
Hydrostatic
Coasting
Analytic Solution
Complication: Heating & Cooling
Mass flux
Radiative Processes

Heating
Inelastic Compton Scattering
Ionisation
lines
Inelastic Compton Scattering
Cooling
free free
free bound
lines
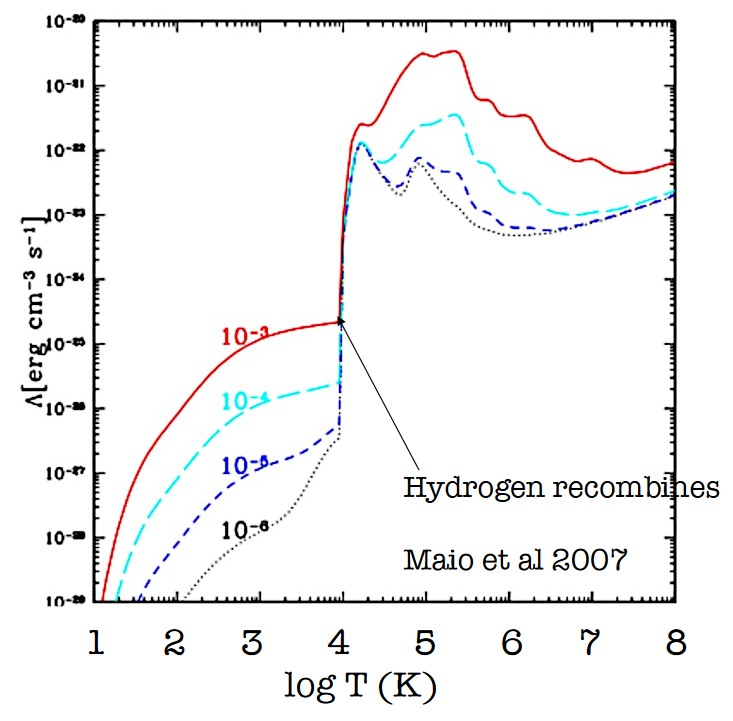
Cooling Function
Difficulty in cooling past 10,000 K
Minimum Pressure
High densities
constant temperature
Low densities
ff cooling
minimum pressure
Temperature Scales
Escape temperature
Inverse Compton temperature
Characteristic temperature
Temperature Scales
Escape temperature
Inverse Compton temperature
Characteristic temperature
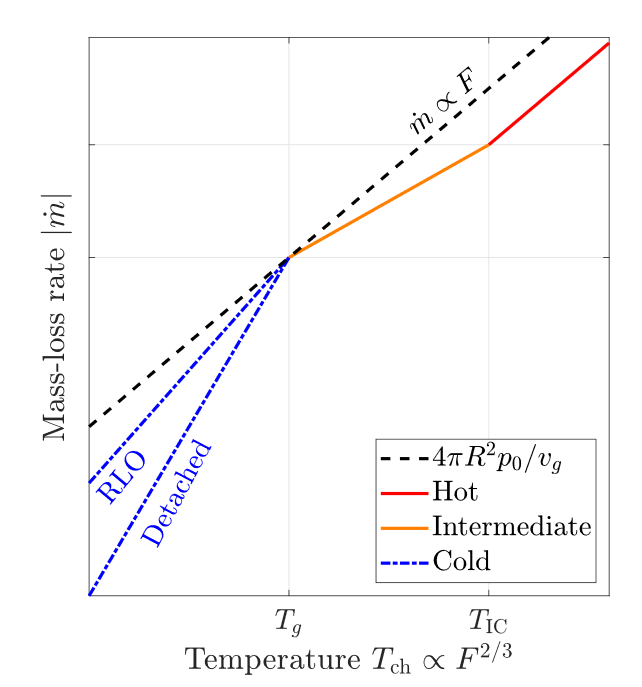
Hot Wind
Sonic point is extremely close to the surface
Mass loss rate
Intermediate Wind
Sonic point is withing a few stellar radii
Mass loss rate
Cold Wind
Sonic point is much larger than stellar radius
speed of sound
velocity
mass loss
Roche Lobe Overflow
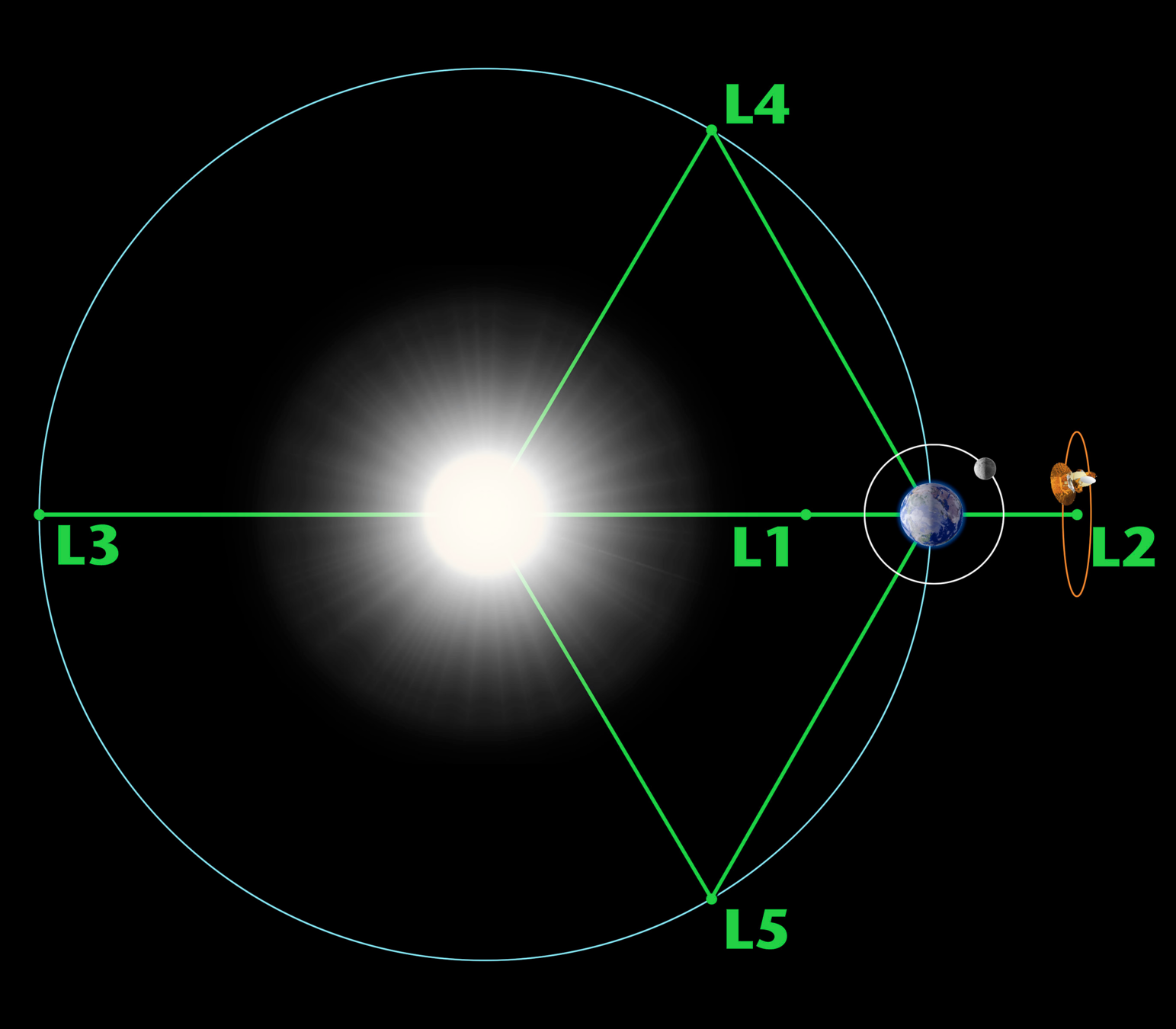
Gas escapes through narrow angle
Net mass loss
Mass Loss
Application
Characteristic temperature from Compton heating
Efficiency
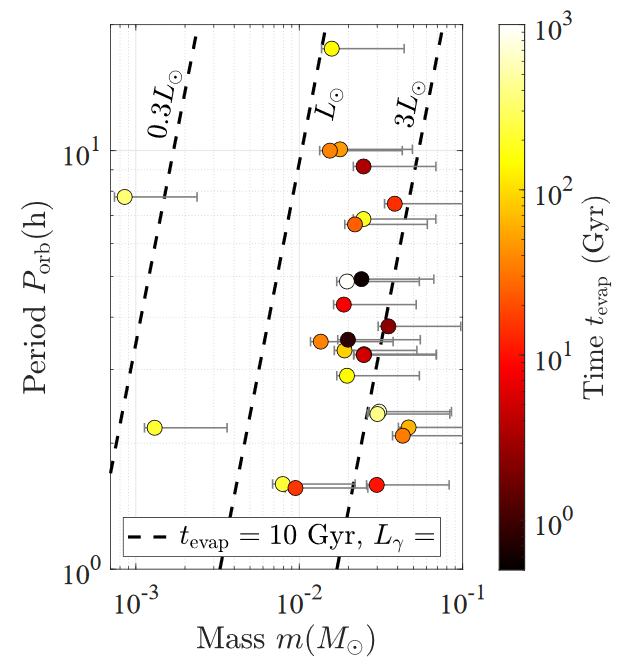
Evaporation time
Comparison to Observations
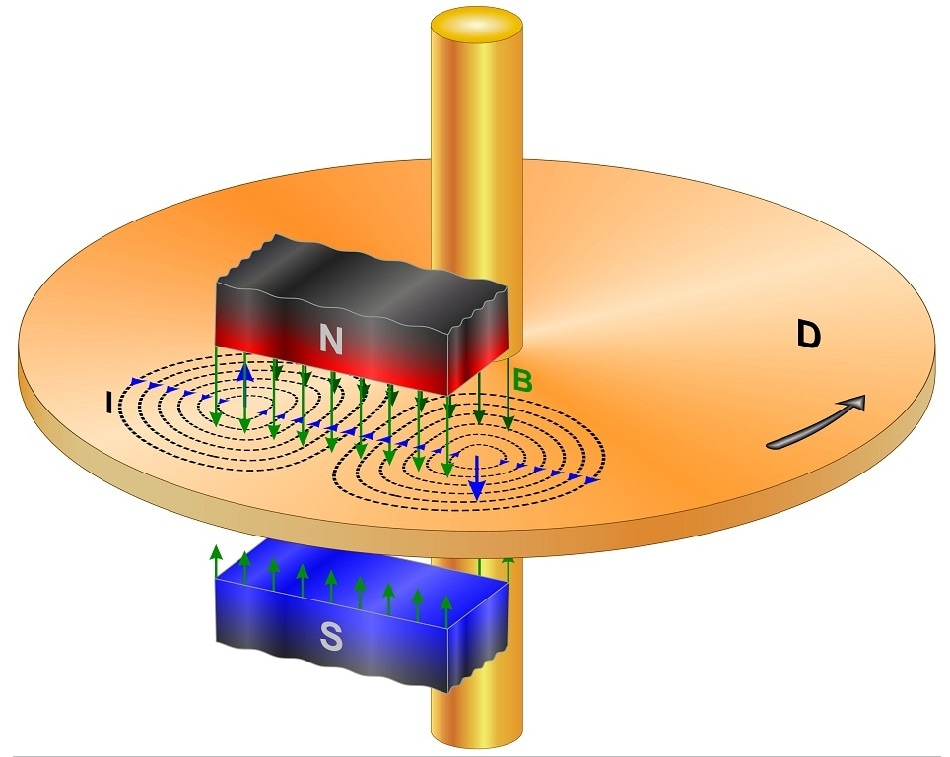
Magnetic Braking
Overview
Synchronised
Lagging
Magnetic breaking
compensation from orbital angular momentum
Net result: Depletion of orbital angular momentum
Alfven Radius

Split monopole magnetic field
equilibrium between magnetic and ram pressure
Sun Spin Down
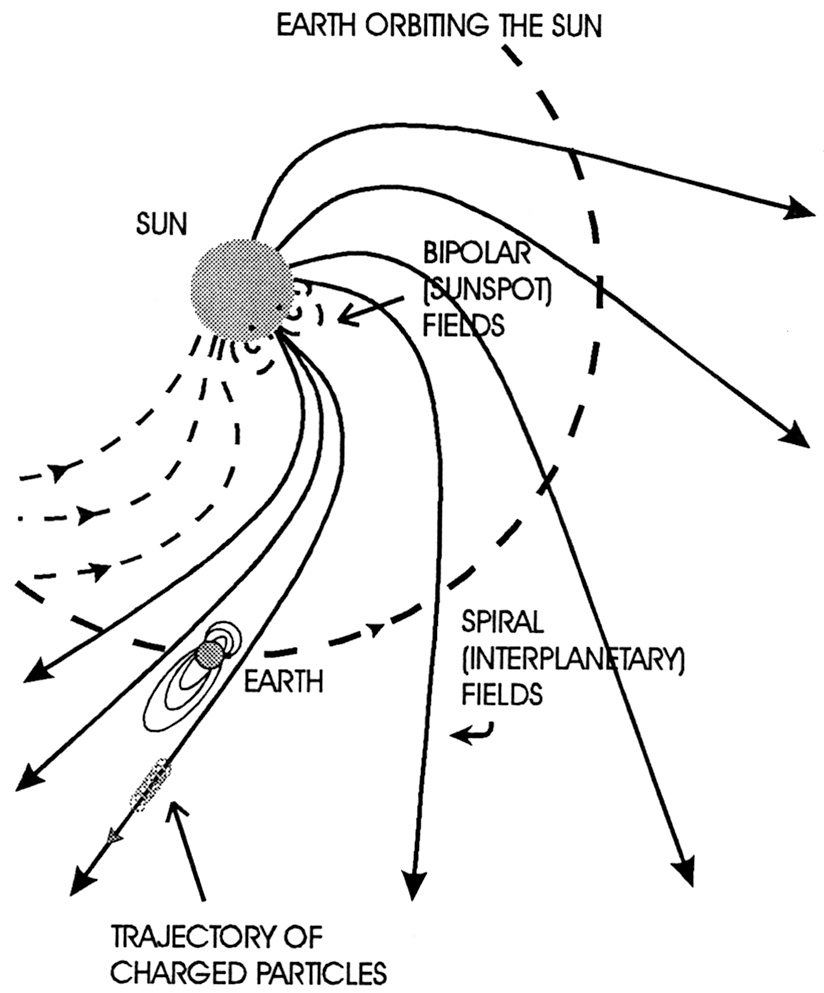
Matter is co - rotating up to the Alfven radius, so mass loss required for factor of two spin - down is
Spin Down Time
Evaporation time determined by
Comparison to Observations
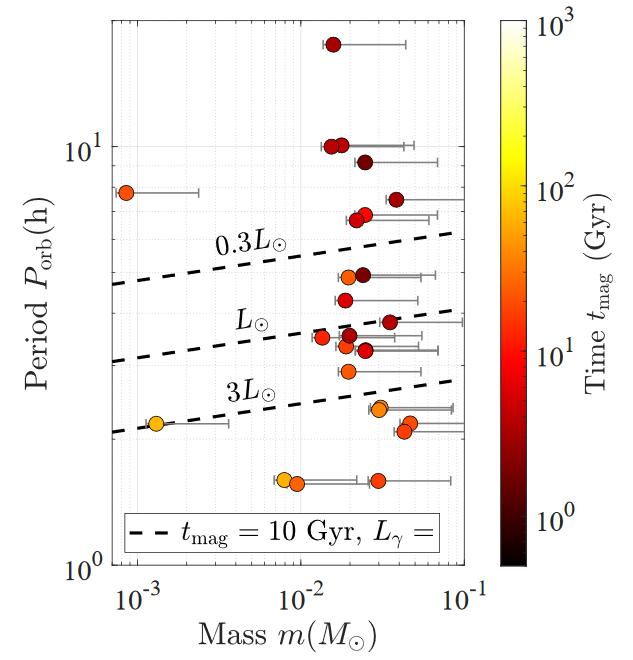
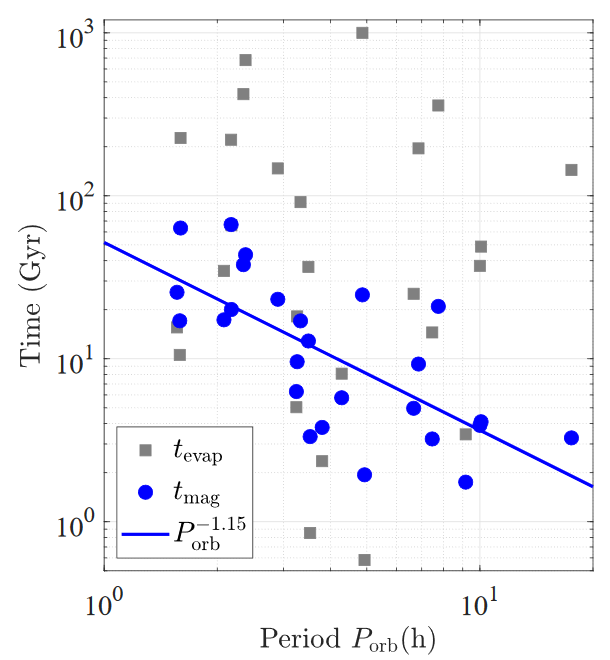
Conclusion
Evaporation with fixed orbital parameters is too slow to explain observations
mass loss is regulated by magnetic braking
questions?