Text
#Matriz a llenar con las probabilidades de transición
m = numpy.zeros((452, 452), numpy.float32)
with open('/Users/agutierrez/Documents/maestria/statistical-computing/compstat2016/proyecto/2016-09.csv', 'rb') as csvfile:
rows = csv.reader(csvfile, delimiter=';')
rows.next()
for row in rows:
# I don't want to consider odd station numbers such as 1002
if int(row[3]) > 500 or int(row[6]) > 500:
pass
# If we hit this else
else:
station_in = int(row[3]) - 1
station_out = int(row[6]) - 1
m[station_in][station_out] = m[station_in][station_out] + 1.0
#Convertimos a probabilidades
m_normalized = m / m.sum(axis=1,keepdims=True)
#Elevando la matríz de transición para obtener la estacionaria
m_powered = numpy.linalg.matrix_power(m_normalized, 100)
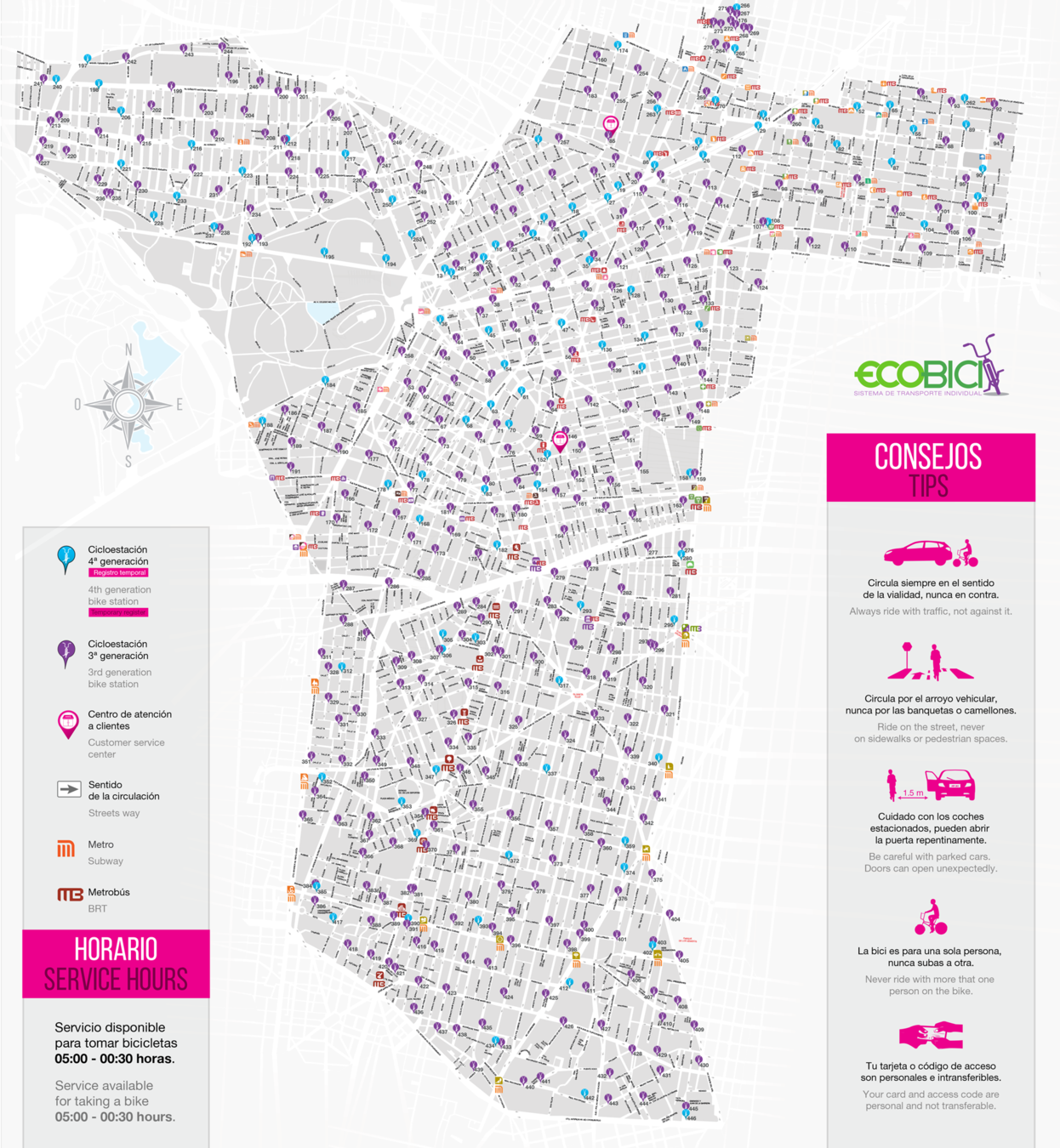
38%
62%
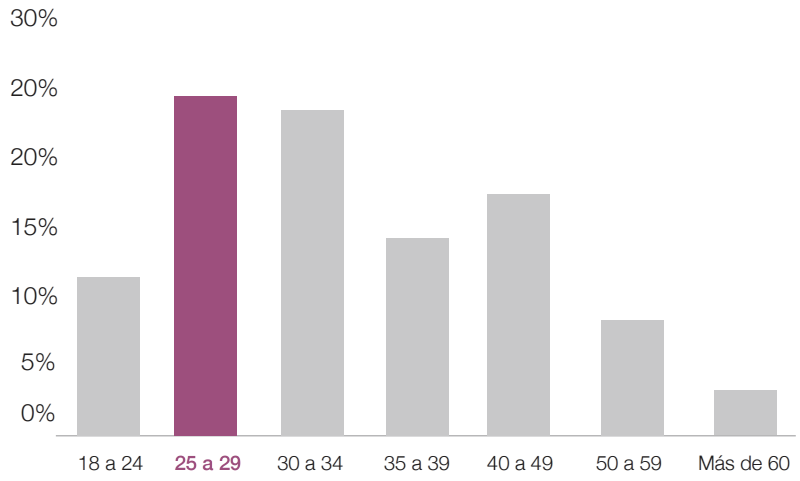
Edad
Modo de transporte
13%
de los viajes se realizan sólo en EcoBici
de los viajes se
combinan con otros modos de transporte
87%
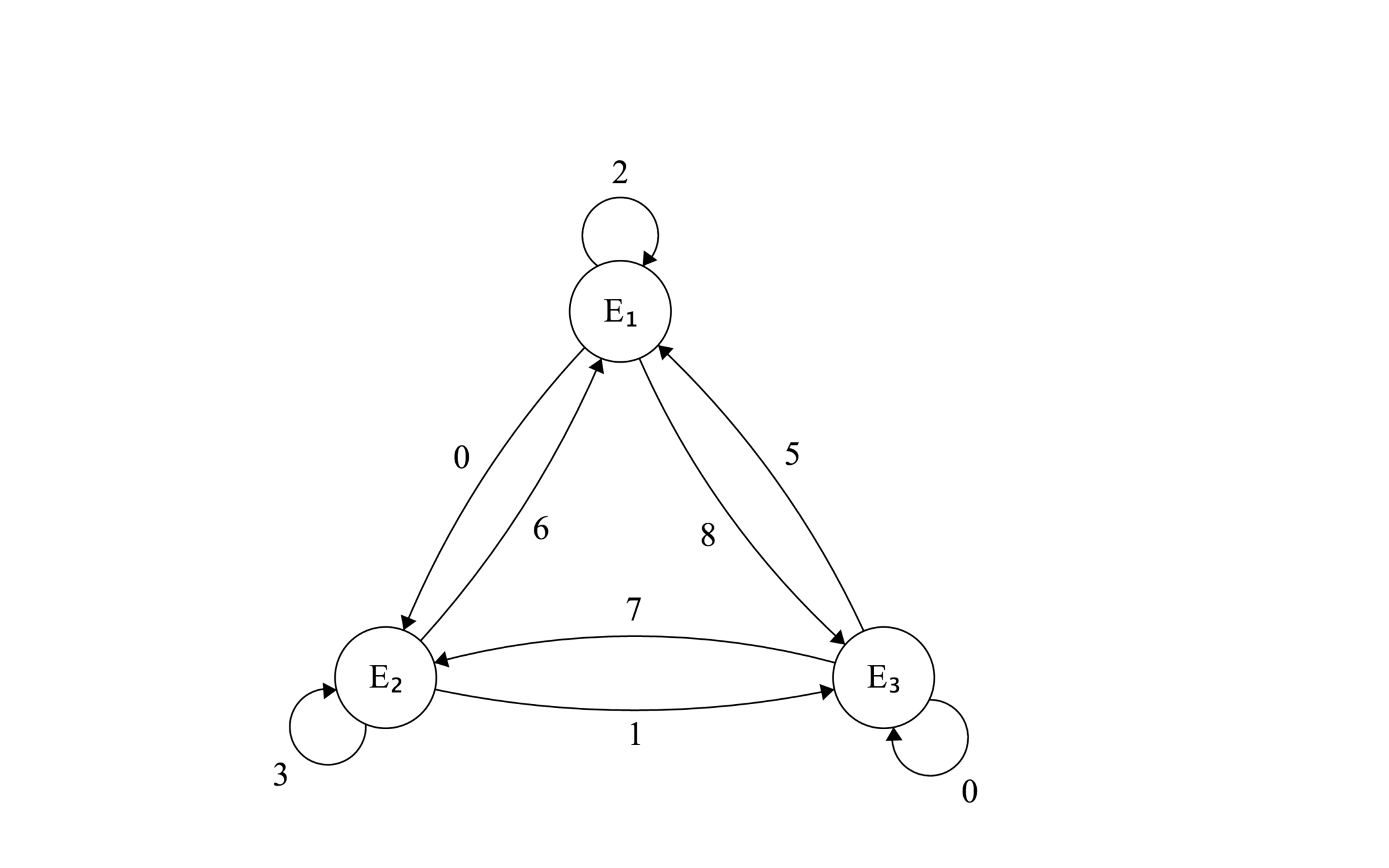
\left( \begin{array}{ccc}
2 & 0 & 8 \\
6 & 1 & 3 \\
5 & 7 & 0 \end{array} \right)
\left( \begin{array}{ccc}
0.2 & 0 & 0.8 \\
0.6 & 0.3 & 0.1 \\
0.42 & 0.58 & 0 \end{array} \right)
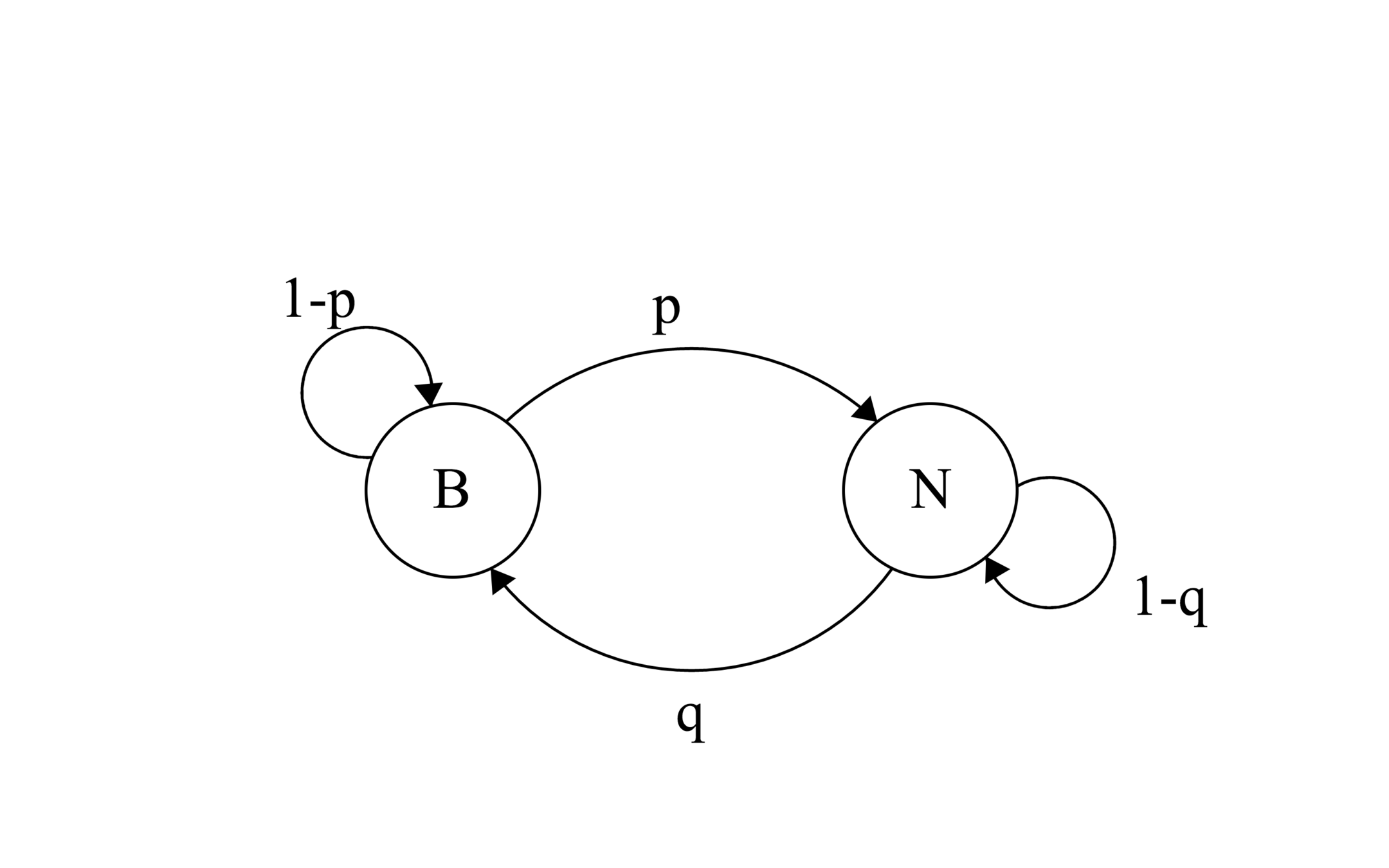
\left( \begin{array}{cc}
1-p & p \\
q & 1-q \end{array} \right)
\lim_{n\rightarrow\infty}\left( \begin{array}{cc}
p & 1-p \\
1-q & q \end{array} \right)^n = \left( \begin{array}{cc}
\frac{q}{p+q} & \frac{p}{p+q}\\
\frac{q}{p+q} & \frac{p}{p+q}\end{array} \right)
P(x)\approx \frac{n_x}{n_i}
Cadenas de Markov
Una cadena de Markov es una serie de eventos, en la cual la probabilidad de que ocurra un evento depende del evento inmediato anterior.
\lim_{n\rightarrow\infty}\left( \begin{array}{ccc}
0.2 & 0 & 0.8 \\
0.6 & 0.3 & 0.1 \\
0.42 & 0.58 & 0 \end{array} \right)^n=\left( \begin{array}{ccc}
0.38 & 0.28 & 0.34 \\
0.38 & 0.28 & 0.34 \\
0.38 & 0.28 & 0.34 \end{array} \right)