Trainable Transformer in Transformer

Amin

July 2023

In-Context Learning

In-Context Learning?

• Happens when language models “learn” from given training exemplars in the context and subsequently predict the label of a test example within a single inference pass.
• Is believed to occur when the large (“simulator”) model mimics and trains a smaller and simpler auxiliary model inside itself.
• This work: An efficient(-ish) architecture capable of doing GD within itself and doing In-Context Learning (ICL), only using the components existing in Transformers.

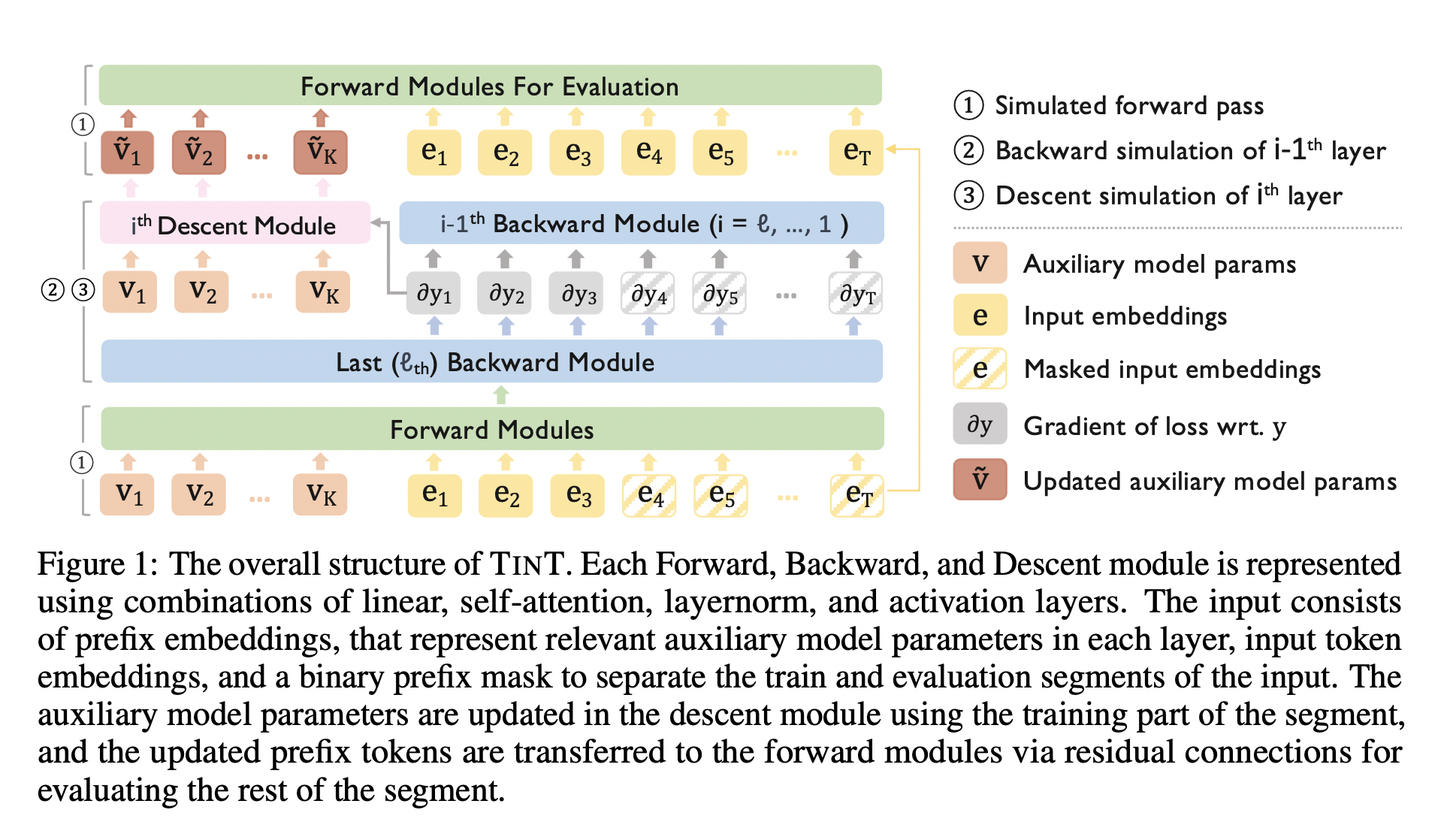
TinT

Main Idea

• Linear, LayerNorm and Attention modules can all be implemented with a self-attention layer.
   
• Weights of the auxiliary model can be stored (and loaded from) the designated prefix embeddings.
   
• Back-propagation on the mentioned modules can be approximated with a self-attention layer.
   
• The approximation is terrible, but works in practice, which suggests that real models might not do actual "Gradient Descent", but something close to it.

Linear Layers

• Let \(W: D_{aux} \times D_{aux} \) denote the weight and \(x_t\) denote the token being operated on. 
• Naive Implementation:
  • Go through each row of weight matrix sequentially.
  • Put each entry of the row in \(\{v_i\}_{i}\) prefix embeddings.
  • \(x_t\) will be in input embeddings
• More efficient:
  • Stack (shard) the operations by \(S\). The outputs will be sparse, and would need to be rearranged, which requires (not so expensive) computations.

Linear Layers

• To perform the dot product, use a self-attention module:

Layer Normalization

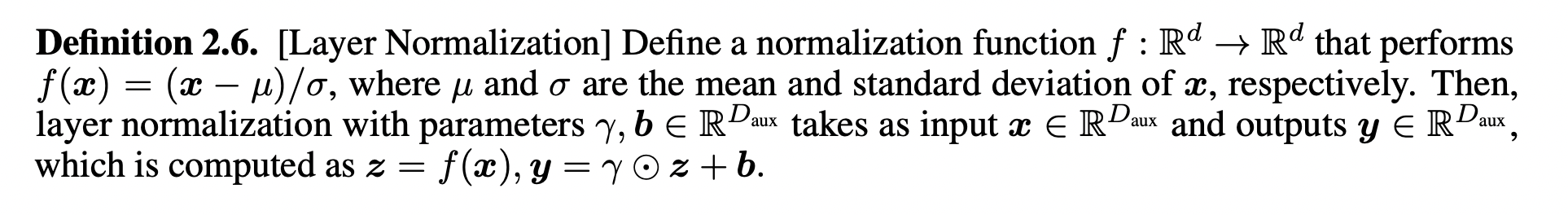
Computing \(\langle \partial_z, z \rangle z\) is expensive, and they instead approximate this gradient with a first-order Taylor approximation.

Layer Normalization

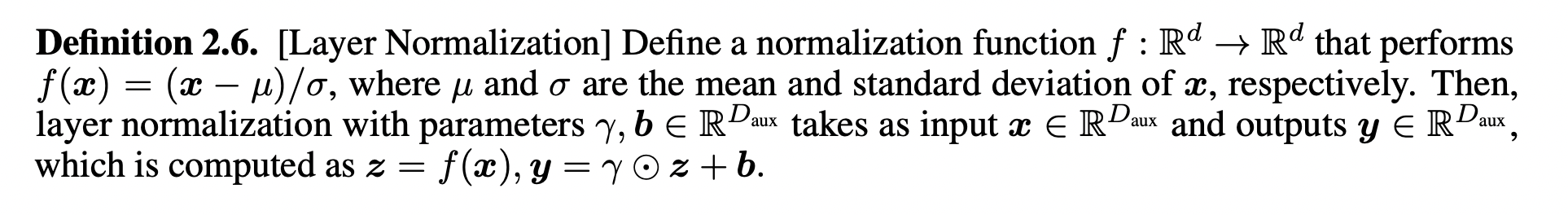
Computing \(\langle \partial_z, z \rangle z\) is expensive, and they instead approximate this gradient with a first-order Taylor approximation.

Softmax Self-Attention

Again, since the computation of \(\partial_{q_t}\) is expensive, they only back-propagate through \(\partial_{v_t}\) to compute \(\partial x_t\).

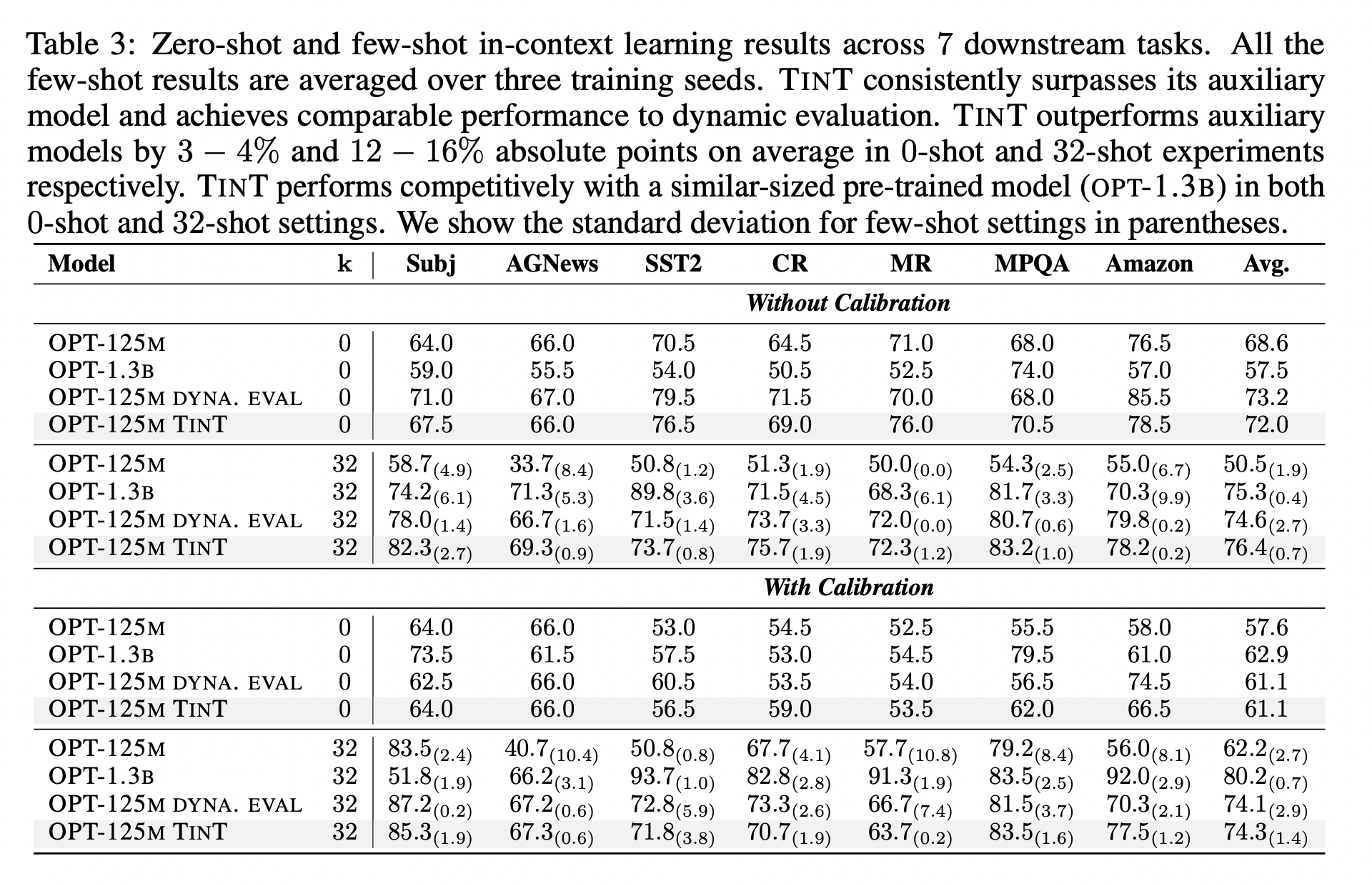
Experiments, Part 1

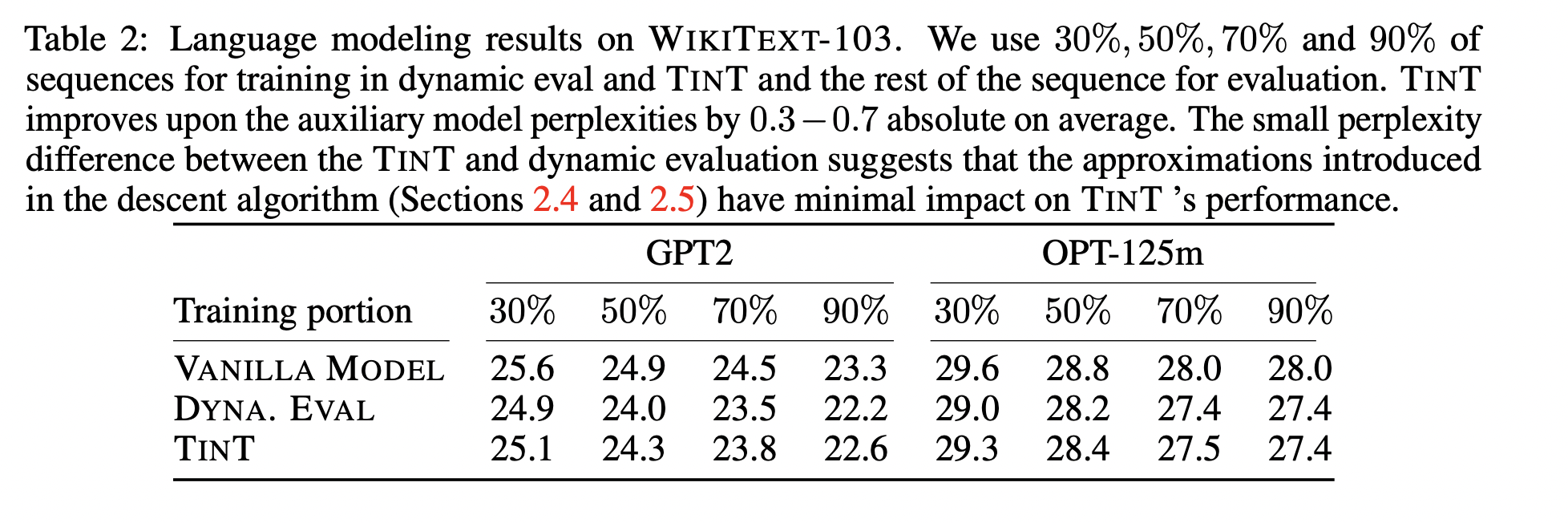
Experiments, Part 2

Implications

• A parameter-efficient architecture designed specifically for ICL is proposed. It requires only about 10x more parameters than the auxiliary model that it contains.
   
• Although 10x more parameters sounds absurd, it's the first proposed architecture that is actually efficient enough to be implemented and tested in practice.
   
• The performance achieved is similar to that of the auxiliary model itself, which suggests they might be going through similar procedures internally.

Thank You!