A Novel Low-Rank Hypergraph
Feature Selection Method
Why Dimension Reduction?
-
Huge datasets
-
More informative data using Multi-View technique
-
Curse of Dimensionality
-
Multi-View data often overfits!
-
Large dimensions often have small cores
Dimension Reduction
-
Subspace Learning
- PCA
- LPP
-
Feature Selection
- Low-Rank Approximation
- Structure Learning
Introduction
-
Low-Rank Constraint
- Reducing noise
- Removing Outliers
- Global Structure
-
Regularization Term
- Sparse Learning
-
Hypergraph Constraint
- Local Structure
Method: Low-Rank Approx.
\underset{over \; W}{minimize} \quad ||Y - XW - eb||_F^2
W: \mathbb{R}^d \times \mathbb{R}^c = AB \, , \, Rank(W) = r
\\
A: \mathbb{R}^d \times \mathbb{R}^r \, , \, AA^T = I
\\
B: \mathbb{R}^r \times \mathbb{R}^c
Method: Adding Regularization
\underset{over \; W}{minimize} \quad ||Y - XW - eb||_F^2 + \lambda ||W||_{2,1}
\\
\\
\text{Bigger } \lambda \longrightarrow \text{More removed features}
Method: Hypergraph
\text{Coefficient Matrix: } \hat{S} = I - D_v^{-\frac{1}{2}}SD_e^{\frac{1}{2}}S^TD_v^{-\frac{1}{2}}
\\
D_v: \text{ Diagonal matrix over column-sum } S
\\
D_e: \text{ Diagonal matrix over row-sum } S
Laplacian: L = D - \hat{S}
\\
D: \text{Diagonal matrix over row-sum } \hat{S}
Method: Hypergraph Contd.
R(W) = \frac{1}{2} \sum_{i,j}^{n} \hat{s}_{ij}||\hat{y}^i - \hat{y}^j||_2^2
\\
\qquad = \cdots
\\
\qquad = tr(B^TA^TXLX^TAB)
Defining Local Structure Parameter:
Method: Objective Function
\underset{over \, A, B, b}{minimize} \quad ||Y-XAB-eb||_F^2
\\
\qquad \qquad \qquad \qquad + \alpha \, tr(B^TA^TXLX^TAB)
\\
\qquad \; + \lambda \, ||AB||_{2,1}
Optimization of the objective
Denote \quad H = I - \frac{1}{n} ee^T
\underset{over \, A, B, b}{minimize} \quad ||Y-XAB-eb||_F^2
\\
\qquad \qquad \qquad \qquad + \alpha \, tr(B^TA^TXLX^TAB)
\\
\qquad \qquad \quad \; \; + \lambda \, tr(B^TA^TDAB)
\text{where } D = diagonal(\frac{1}{2||w^i||_2})
Finding b: Fix A and B
L(b) \text{ derived from the objective}
\\
\frac{\partial{L(b)}}{\partial{b}} = 0
b = \frac{1}{n} e^TY - e^TX^TBA
Finding B: Fix A and b
L(B) \text{ derived from the objective}
\\
\frac{\partial{L(B)}}{\partial{B}} = 0
B = (A^T(XHHX^TA + \alpha XH^LHX^TA))^{−1} A^TXHHY
Finding A: Fix B and b
L(A) \text{ derived from the objective}
\\
\frac{\partial{L(A)}}{\partial{A}} = 0
max\_A = (A(XHHX^T + \alpha XHLHX^T + \lambda D))^{−1} A^TXHHYY^THHX^TA
Selected Features
We've found W, which:
-
Shows association of two features
-
Shows removed (zeroed) redundant features
-
Can be used to construct new dataset
Sample Results with SVM
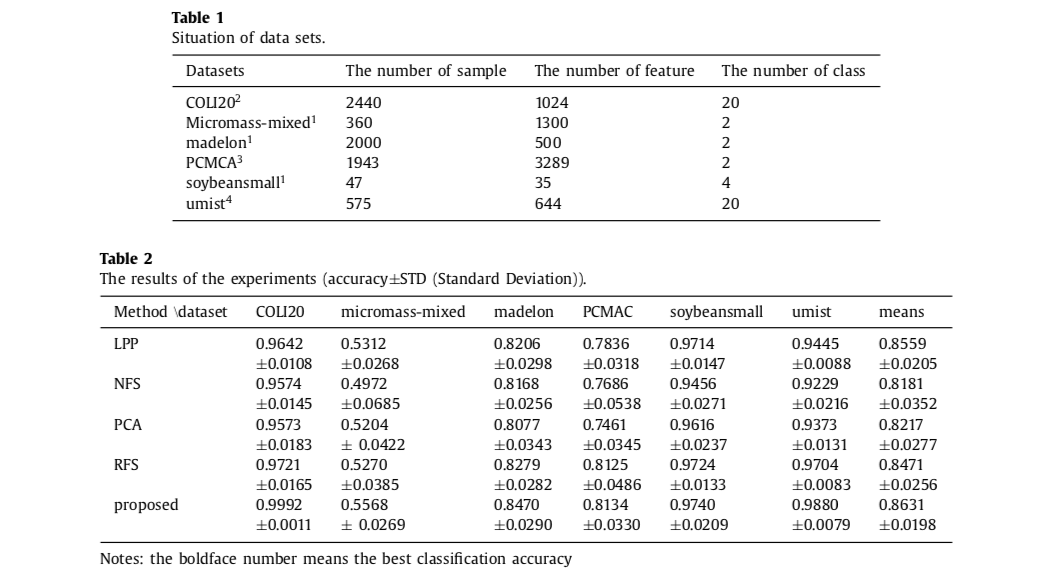
Questions
-
Why can't we just use splines instead of hypergraphs? (Splines + Low-Rank Approx. + Regularization)
-
Why can't we just use local regression instead of hypergraphs?
