INTRODUCTION:

THREATS VS. ASSUMPTIONS

INTRODUCTION: THREATS VS. ASSUMPTIONS

• Why generalization?
   
• Arbitrary or drastically different environments
   
• Sufficiently similar environments
   
• Prior methods:
  • Meta analysis
  • Hierarchical models
• Rarely make explicit distinction between experimental and observational regime

INTRODUCTION: THREATS VS. ASSUMPTIONS

• This paper:
   
  • Limits on what can be achieved in practice
     
  • Problems that are likely to be encountered when populations differ significantly
     

  • What population differences can be circumvented
     

  • What differences constitute theoretical impediments

INTRODUCTION: THREATS VS. ASSUMPTIONS

• Standard literature:
   
  • Studying threats over licensing assumptions. Why?
     
    • Safer to cite, little risk related to endorsing something
    • Assumptions are self-destructive in their honesty.
    • Threats can be communicated in plain English

INTRODUCTION: THREATS VS. ASSUMPTIONS

• Create licenses to transport using:
  • Causal diagrams
  • Models of interventions
  • Counterfactuals
     
• ​Using Do-Calculus to:
  • T​est the feasibility of transport
  • Estimating causal effects in the target population

 PRELIMINARIES: THE LOGICAL FOUNDATIONS OF CAUSAL INFERENCE

 PRELIMINARIES: THE LOGICAL FOUNDATIONS OF CAUSAL INFERENCE

• (nonparametric) Structural Equations Models (SEM)

Causal Models as Inference Engines

• Causal assumptions 
• An inference engine

Assumptions in Nonparametric Models  (SEM)

• A set U of background or exogenous variables, representing factors outside the model.
   
• A set V = {V1, . . . , Vn} of endogenous variables, assumed to be observable.
   
• A set F of functions {f1,...,fn} such that each fi determines the value of Vi ∈ V.
   
• A joint probability distribution P(u) over U.

Assumptions in Nonparametric Models  (SEM)

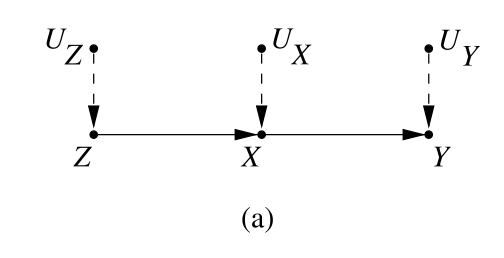
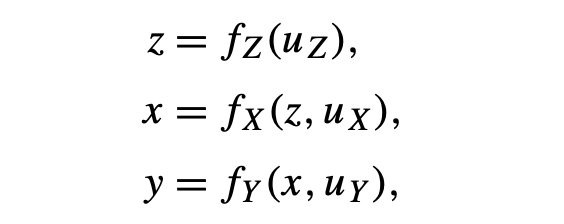
Representing Interventions, Counterfactuals and Causal Effects

• Interventions through a mathematical operator called do(x)
   
• For example, let's use do(x0) on the previous model, now we have:

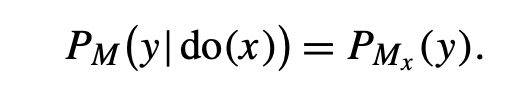
Identification, d-Separation and Causal Calculus 

• Identification in linear parametric settings
   
• Identification in nonparametric formulation
   
• Identifiability:
  • Acausal query Q(M) is identifiable, given a set of assumptions A, if for any two (fully specified) models, M1 and M2, that satisfy A, we have:

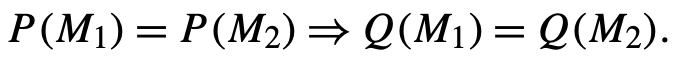
The Rules of do-Calculus 

•     the graph obtained by deleting from G all arrows pointing to nodes in X
•     the graph obtained by deleting from G all arrows emerging from nodes in X.
• Z(W) is the set of Z-nodes
  that are not ancestors of
  any W-node in       .

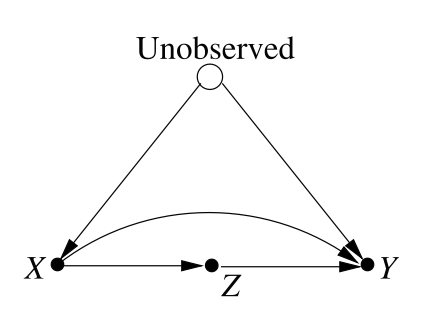
INFERENCE ACROSS POPULATIONS: MOTIVATING EXAMPLES 

Example 1

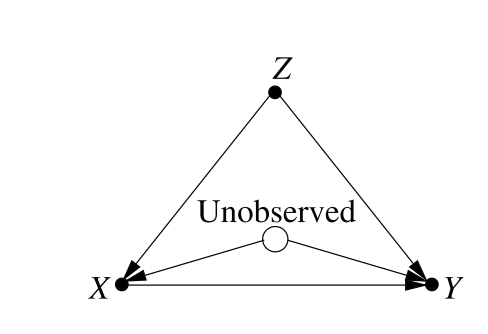
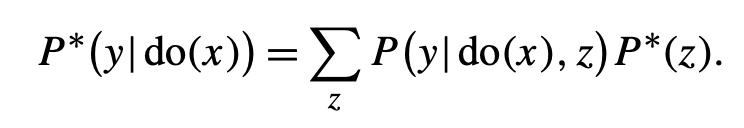
Example 2

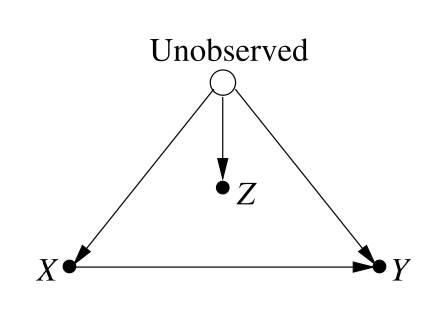
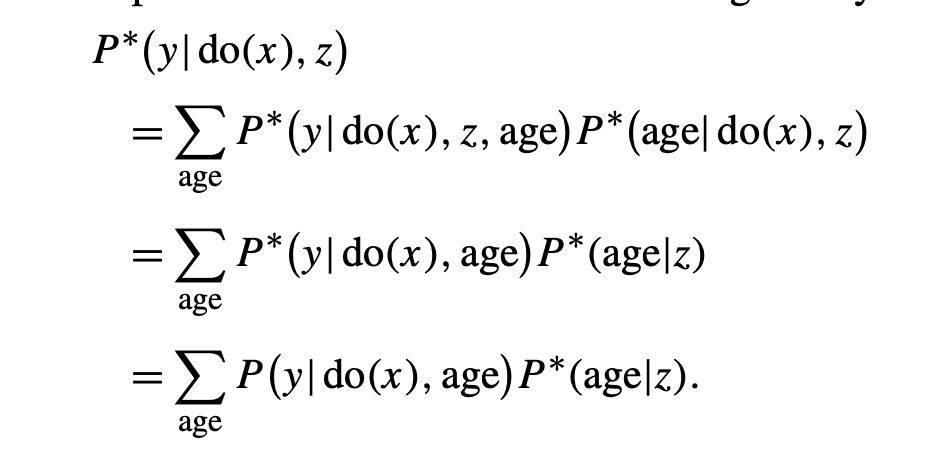
Example 3