Logic-RL
Unleashing LLM Reasoning with
Rule-Based Reinforcement Learning
Amin - March 5 2025
LLM Reasoning Reading Group
Overview
- Train a pre-trained LLM on a class of Logical Puzzles (Knights & Knaves) using Rule-Based Reinforcement Learning.
- Model learns to solve these puzzles using techniques like backtracking, exploring and verifying.
-
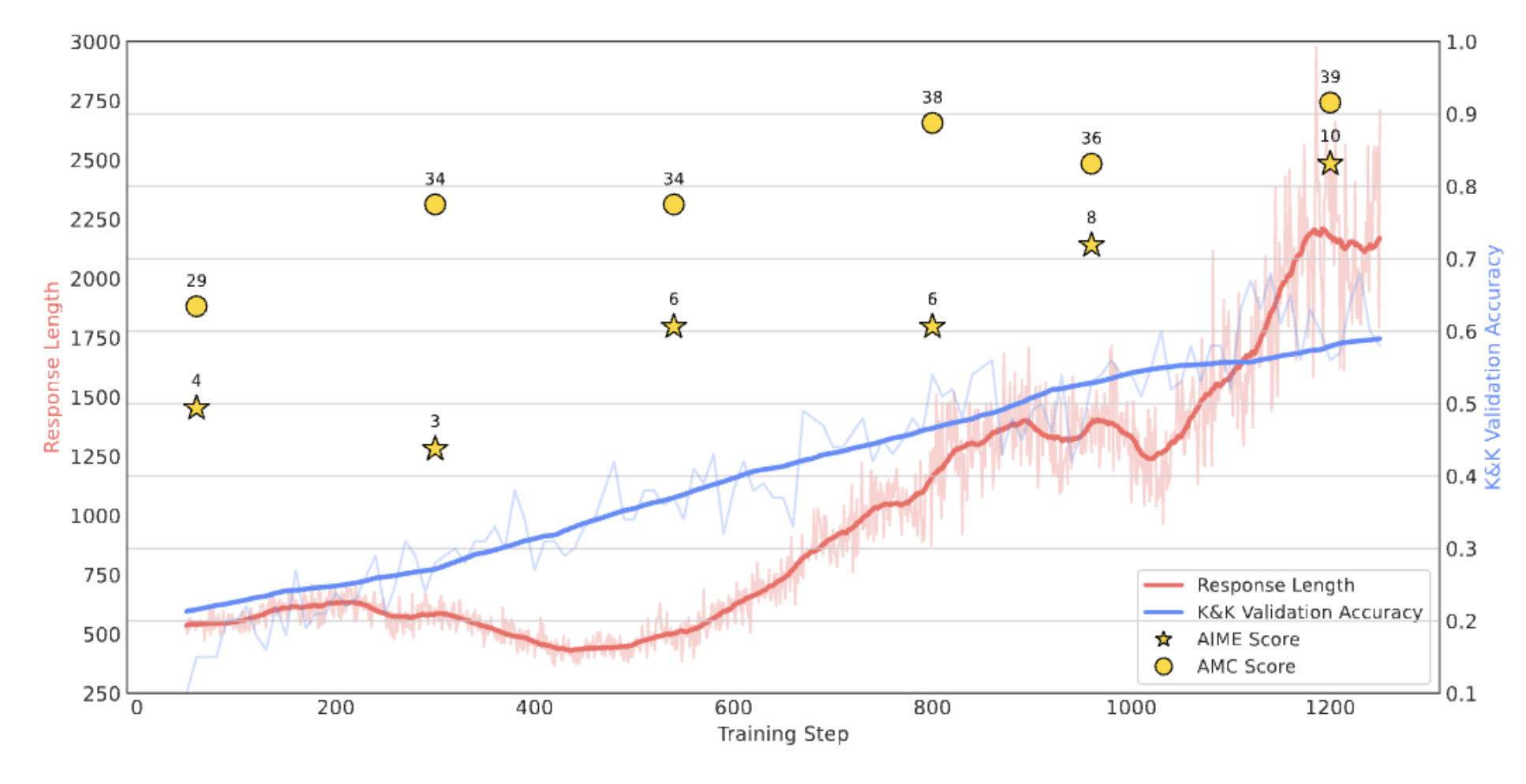
Learnt behaviours seem to extrapolate to other tasks that involve reasoning, namely on AIME and AMC benchmarks.
- Ablation studies stimulate interesting research questions.
Overview
Setup: Problem

- Instances of K&K can be procedurally generated.
- Instances can have varying levels of difficulty.
- Instances are easy to verify (single, unambigouous solutions).
Setup: Reward
- To prevent reward hacking:
- Model is asked to think within </think> and answer within </answer> tags.
- Reward is calculated based on the format and correctness of the response.
S_{\text{format}} =
\begin{cases}
1, & \text{if format is correct} \\
-1, & \text{if format is incorrect}
\end{cases}
S_{\text{answer}} =
\begin{cases}
2, & \text{if the answer fully matches the ground truth} \\
-1.5, & \text{if the answer partially mismatches the ground truth} \\
-2, & \text{if the answer cannot be parsed or is missing}
\end{cases}
Setup: RL Algorithm
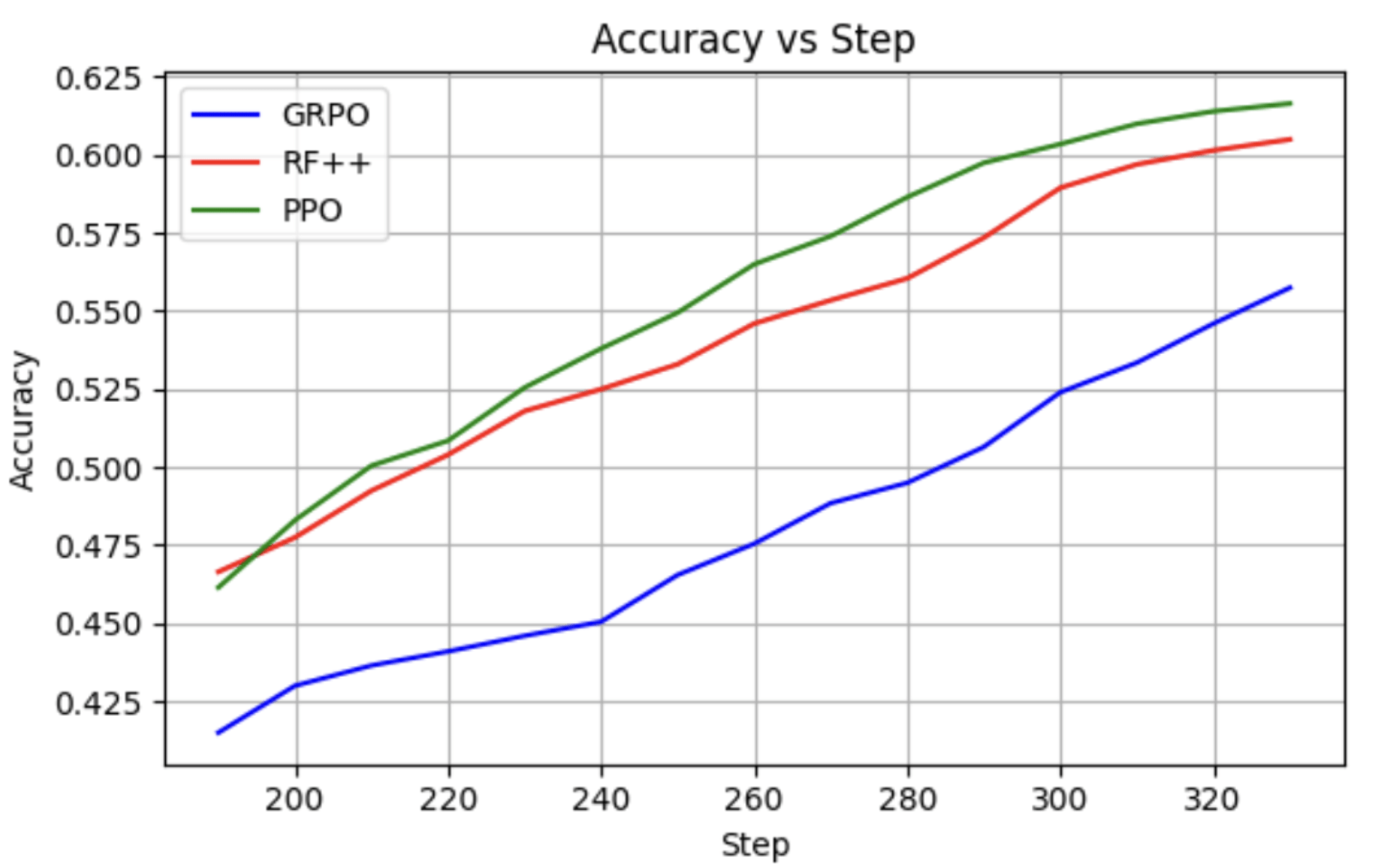
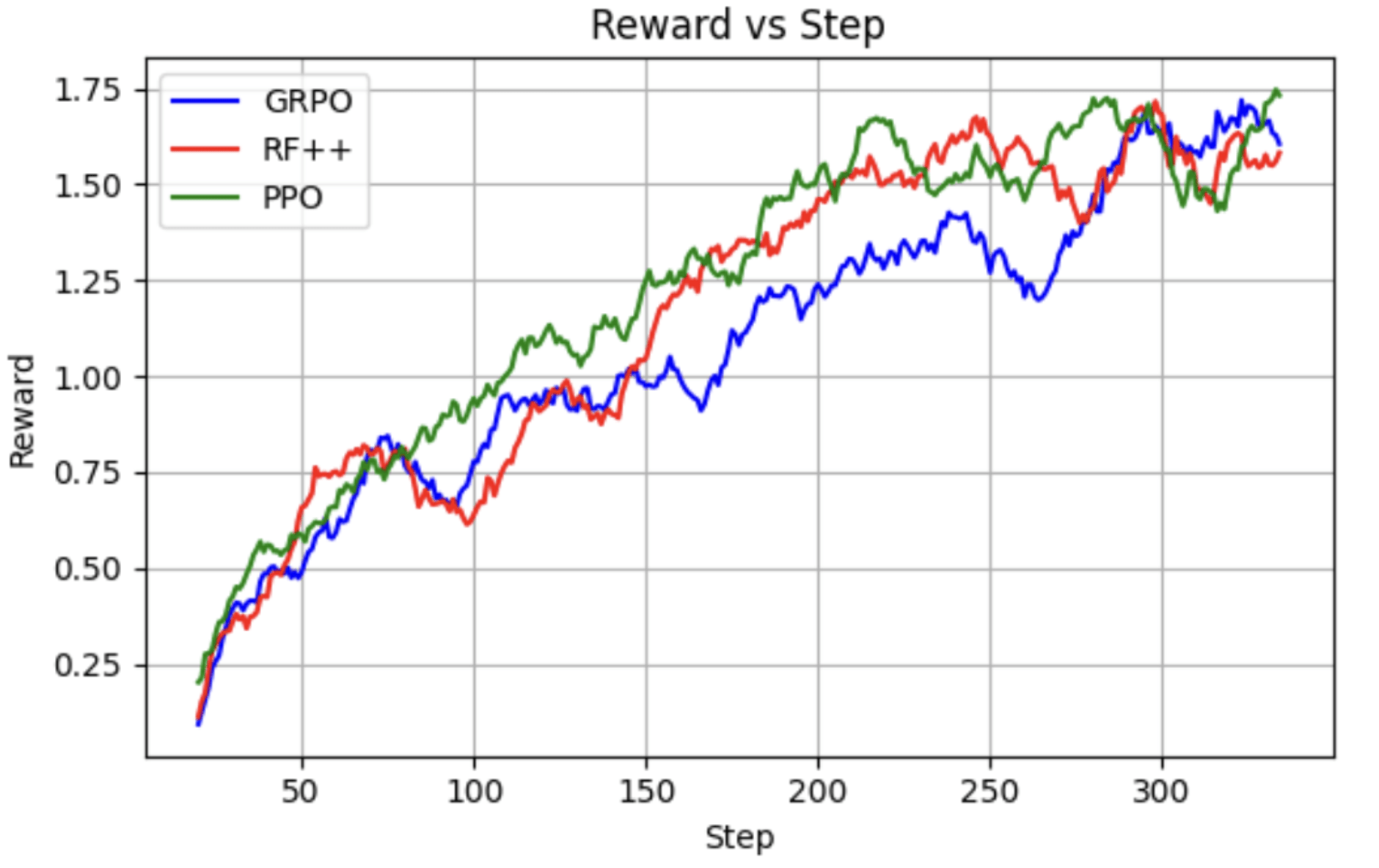
- The algorithm of choice is REINFORCE++ with slight modifications (there are ablations against PPO and GRPO).
-
Modification 1: KL between response distribution of the RL model and the SFT model is calculated on a per-token basis and incorporate in the loss (similar to GRPO, over being part of the Reward).
- Modification 2: An unbiased KL-Estimator similar to that of GRPO is used.
Setup: Hyperparameters
- The model (Qwen2.5-7B) is trained over 3600 steps, with a constant LR of \(4 \cdot 10^-7\) and a temperature of 0.7 on puzzles having mixed complexity and ranging from 3 to 7 people.
- Hyper-parameters used for SFT are not discussed.
- There is no ablation on hyper-parameters.

Background: REINFORCE
- Introduction of the discounted cumulative rewards:
$$G_t = \sum_{k=t+1}^{T} \gamma^{k-t} r_k$$ - The policy gradient is computed as:
$$\nabla_{\theta} J(\theta) = \mathbb{E}_{\pi} \left[ G_t \nabla_{\theta} \log \pi_{\theta} (A_t \mid S_t) \right]$$ - The parameters are updated as:
$$\theta \gets \theta + \alpha \nabla_{\theta} J(\theta)$$ - Simple direct preference optimization algorithm, but suffers from
Background: REINFORCE++
- Addition of token-level KL loss to the reward:
$$\operatorname{KL}(t) = \log \left( \frac{\pi_{\theta_{\text{old}}}^{\text{RL}}(a_t \mid s_t)}{\pi^{\text{SFT}}(a_t \mid s_t)} \right)$$ - PPO-Clip Integration:
$$L^{CLIP}(\theta) = \mathbb{E}_t \left[ \min \left( r_t(\theta) \hat{A}_t, \operatorname{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right) \right]$$ - Reward Normalization
$$r_t(\theta) = \frac{\pi_{\theta}(a_t \mid s_t)}{\pi_{\theta_{\text{old}}}(a_t \mid s_t)}$$ - Advantage Normalization
$$A_t(s_t, a_t) = r(x, y) - \beta \cdot \sum_{i=t}^{T} \operatorname{KL}(i)$$
Results
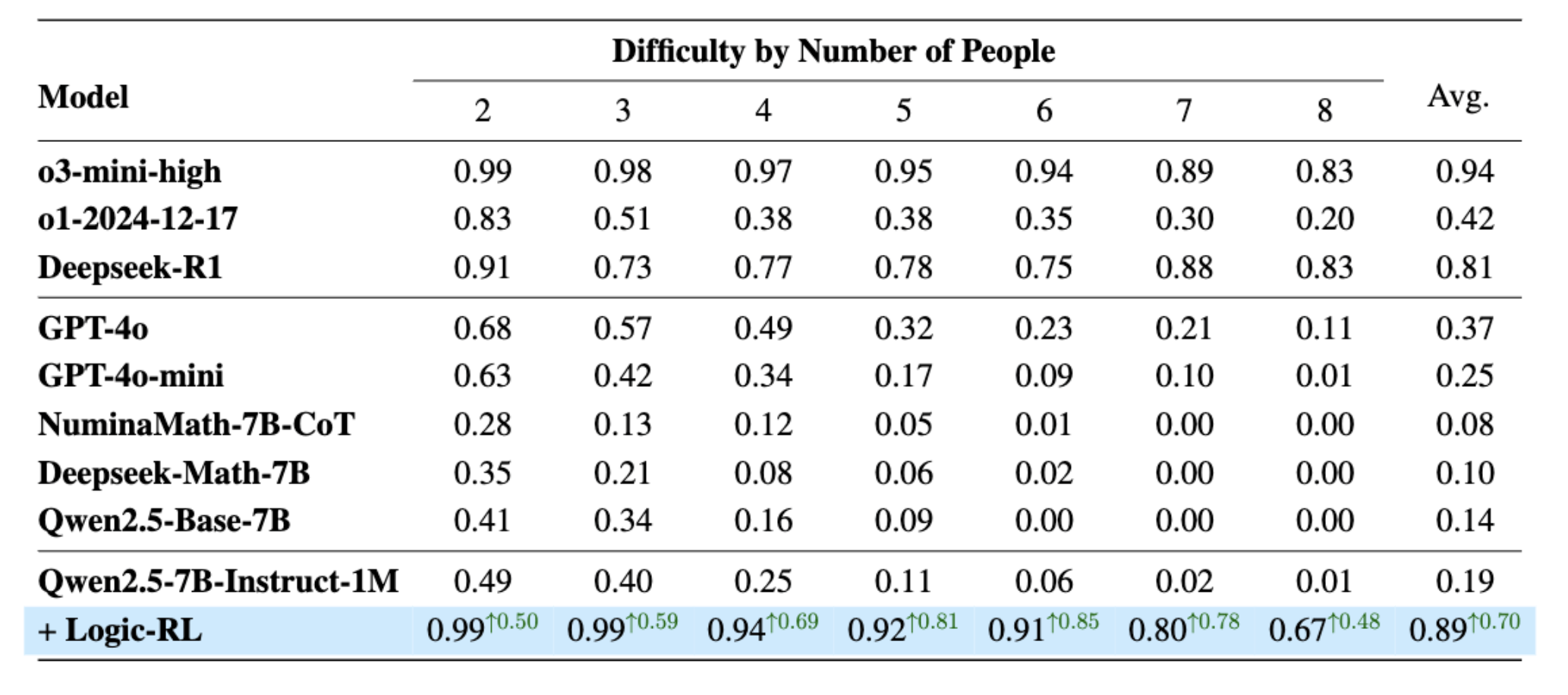
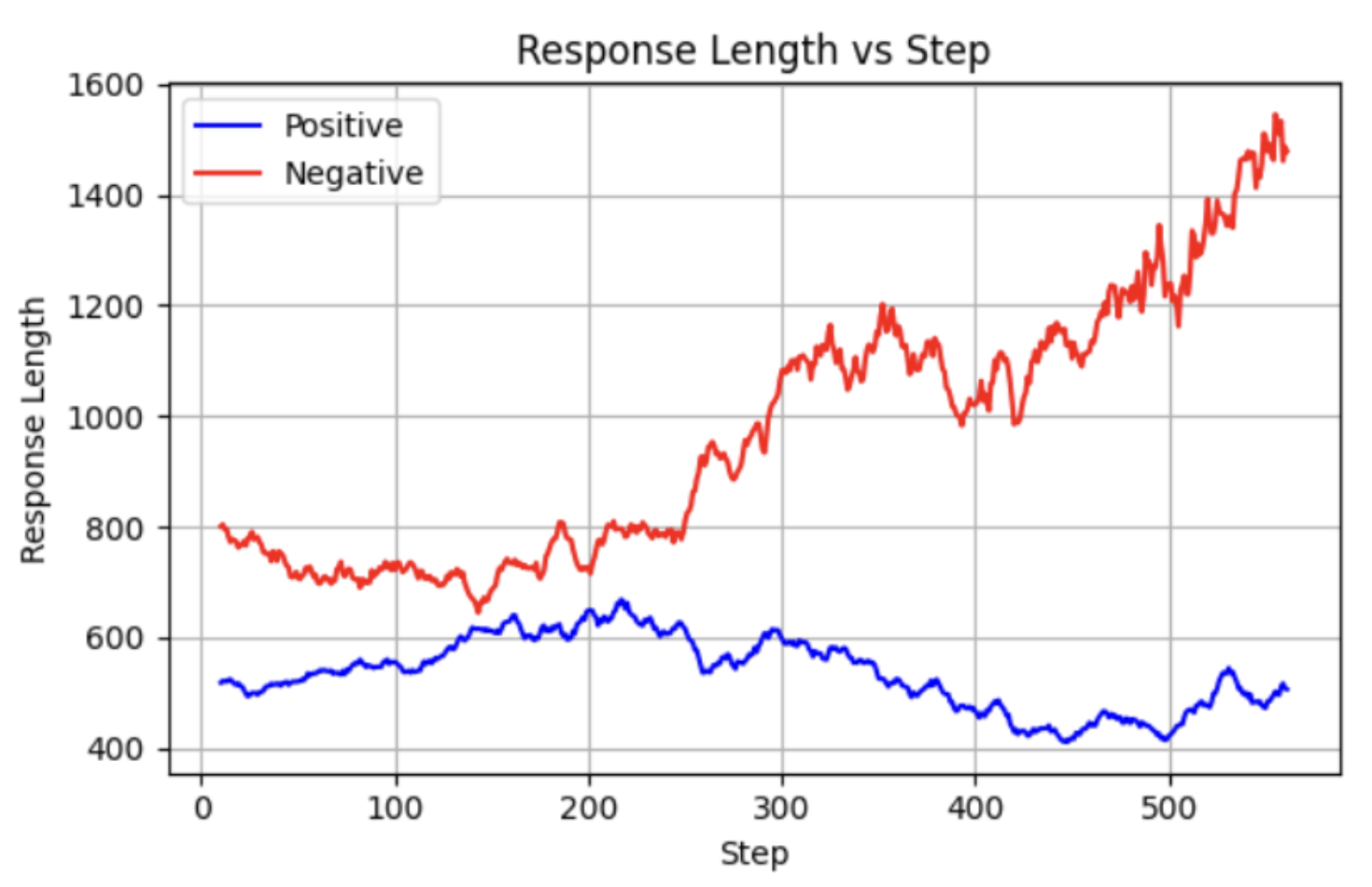
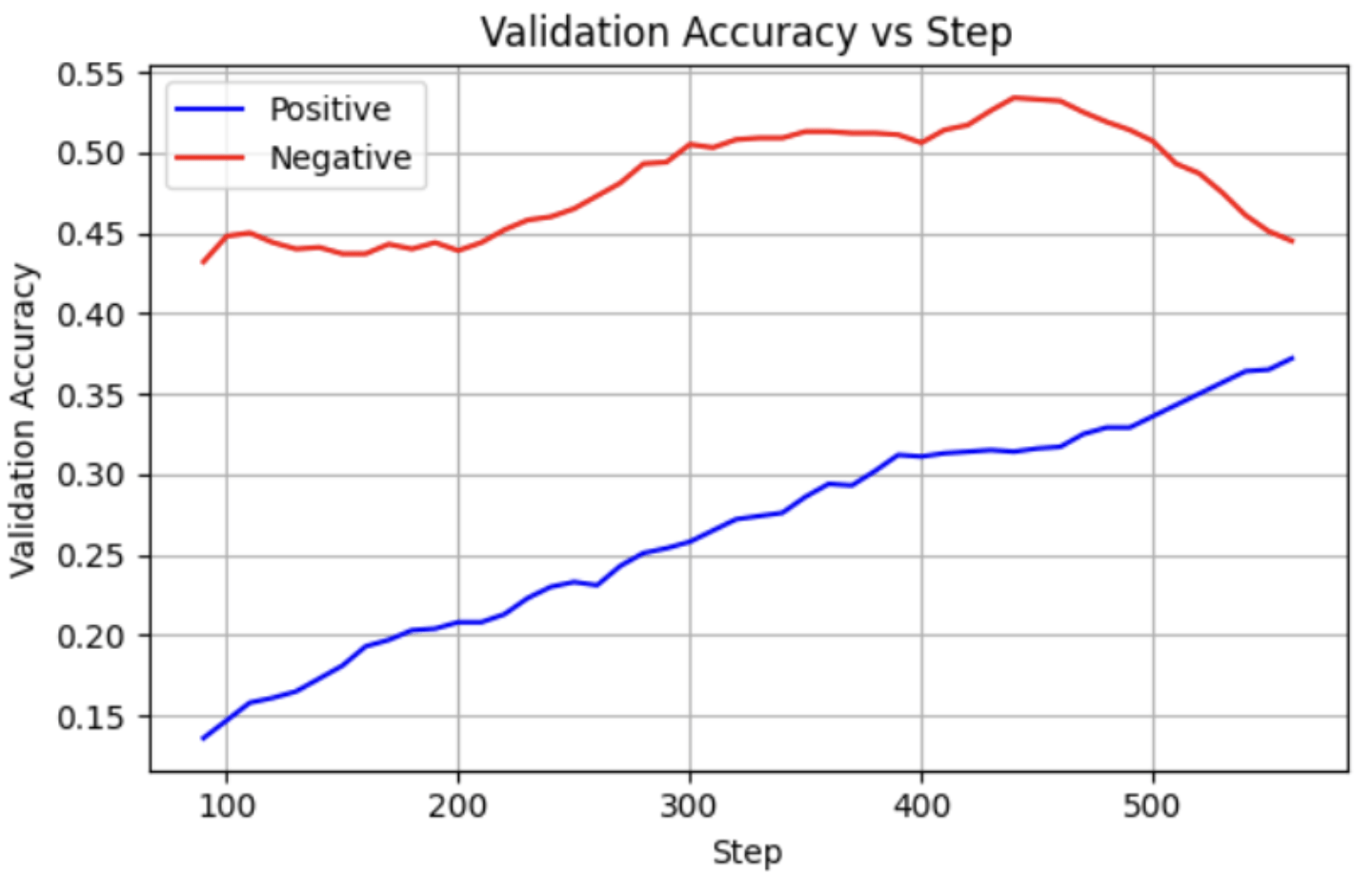
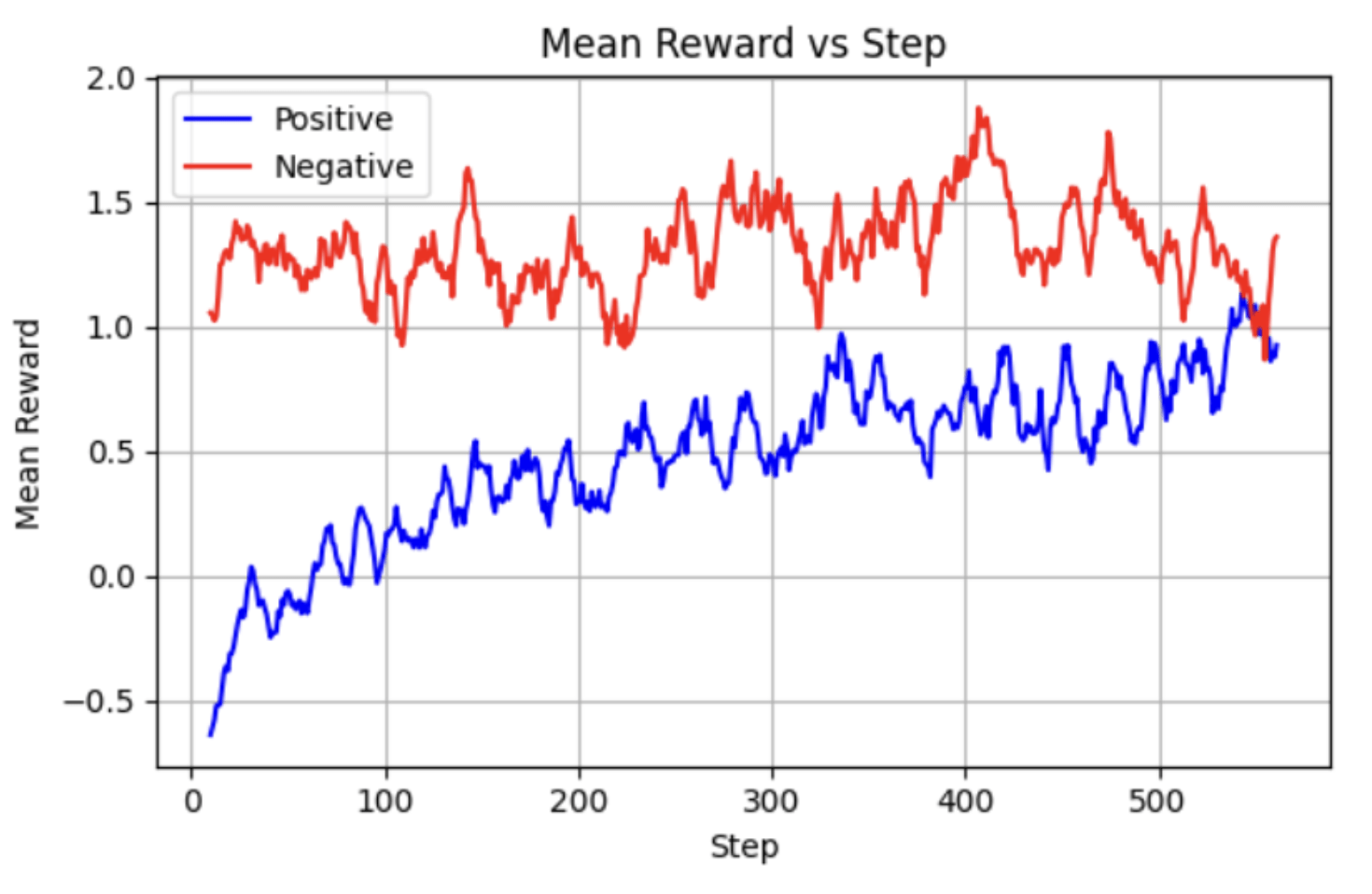
RQ-1: The RL Algorithm

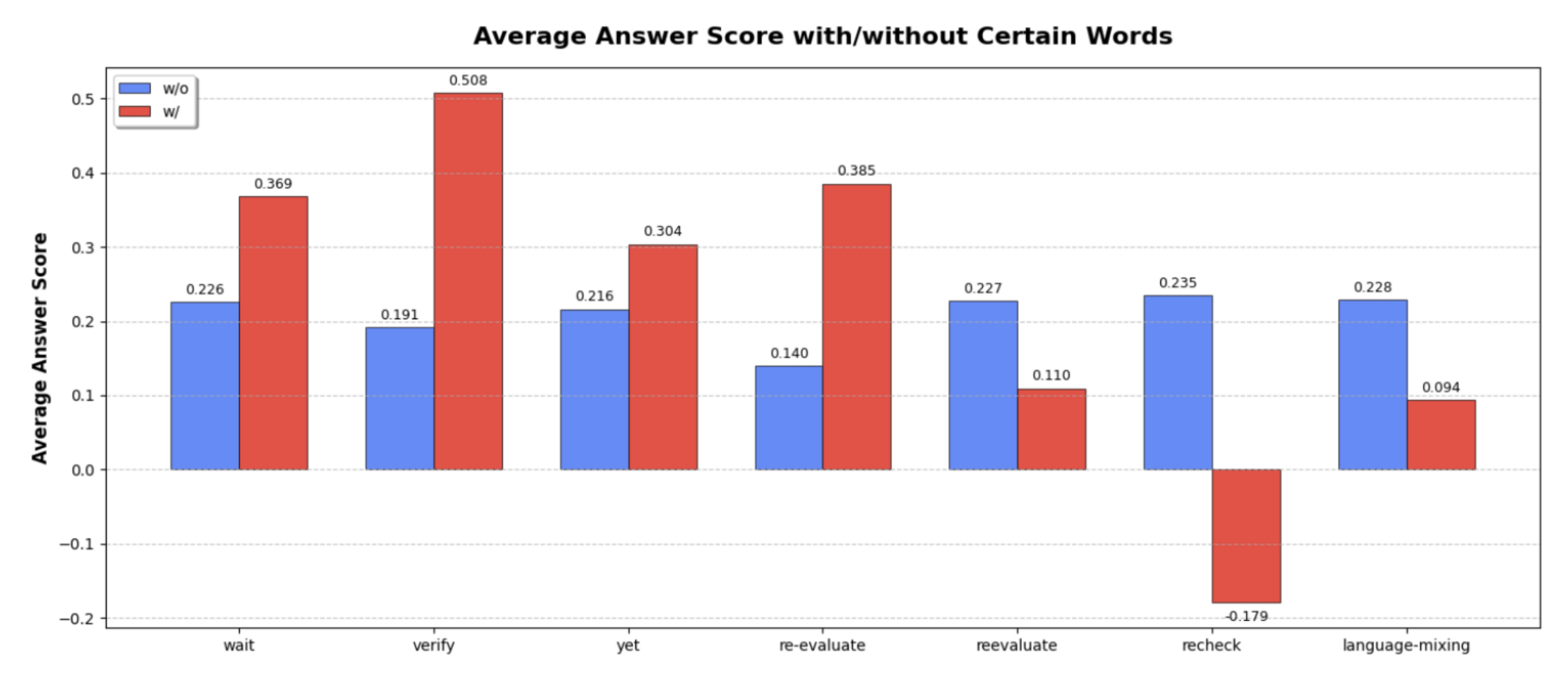
RQ-2: Thinking Tokens
RQ-3: Is there an Aha moment?
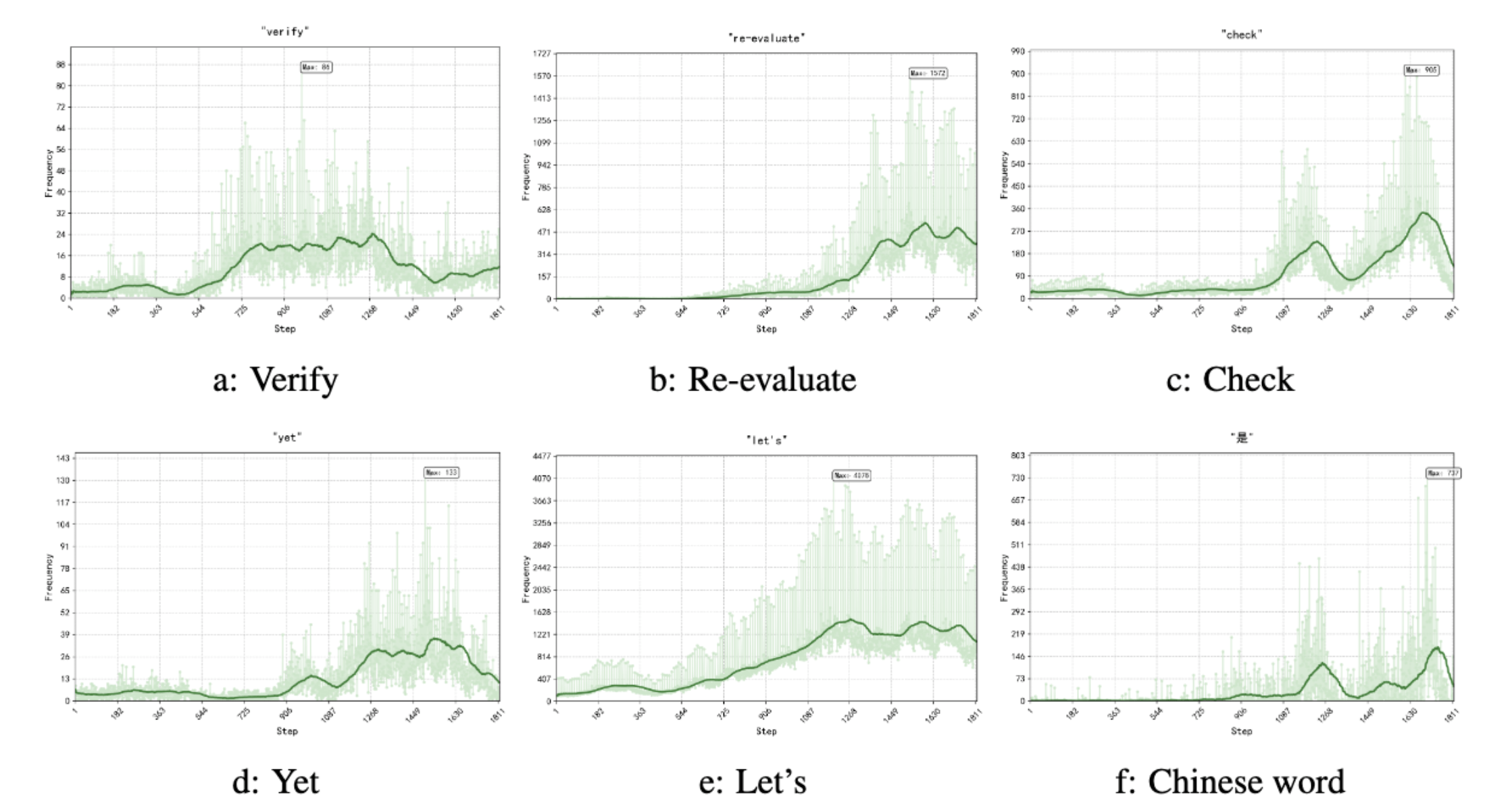
RQ-4: Does Logic-RL Generalize?
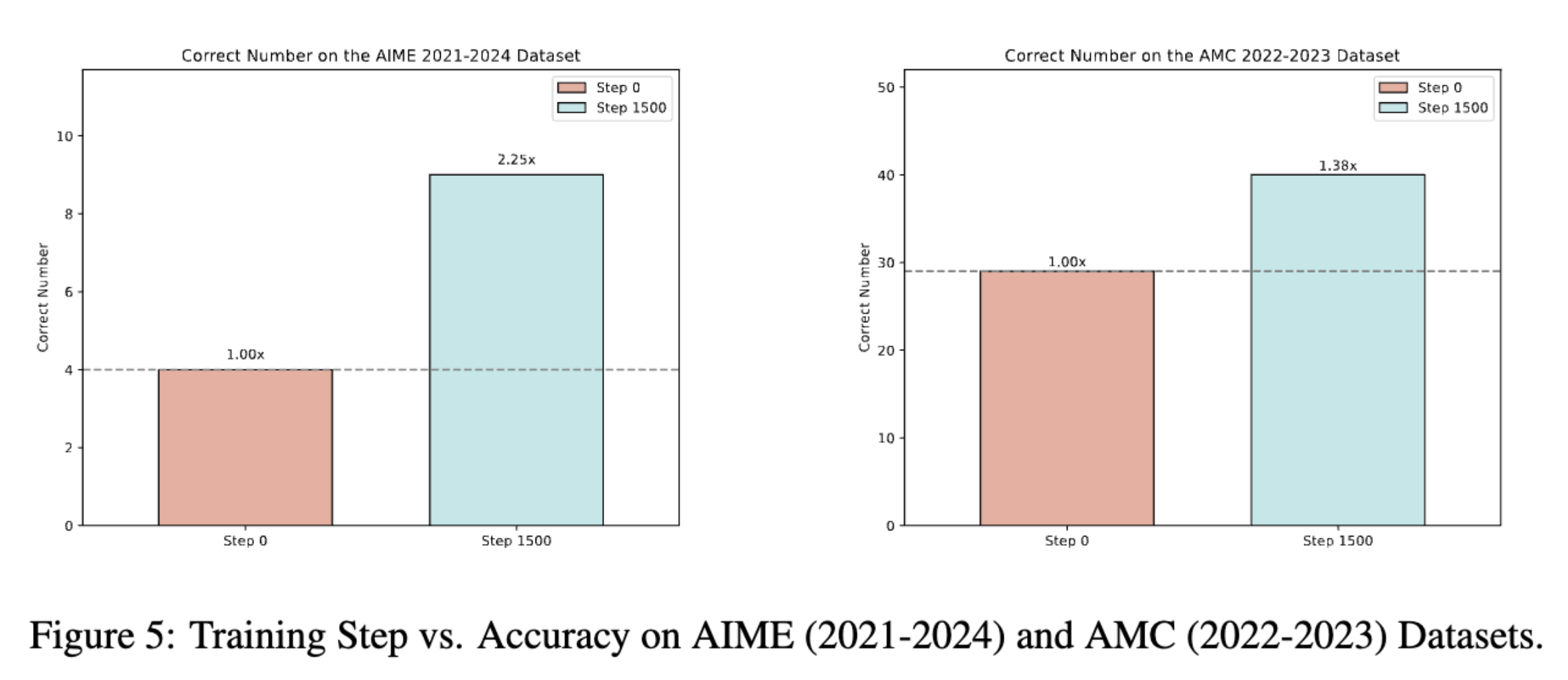
RQ-5: Robustness to Perturbation - SFT vs RL

RQ-5: Robustness to Perturbation - SFT vs RL
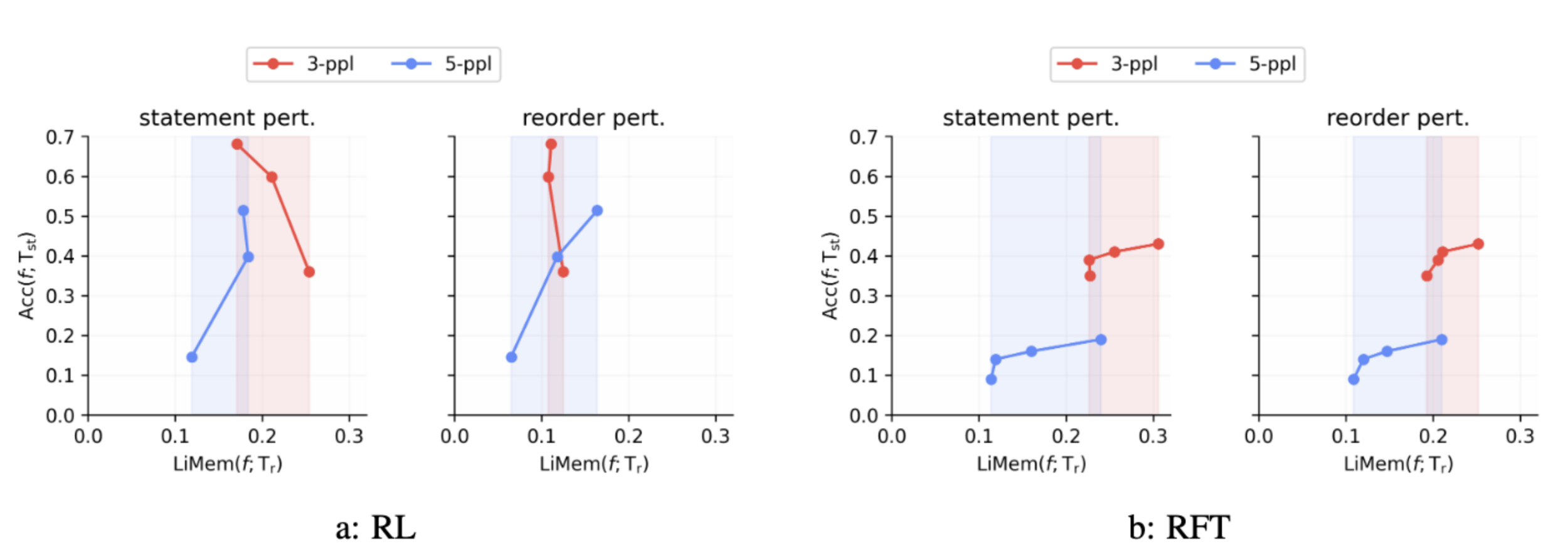
\text{LiMem}(f; \mathcal{D}) = \text{Acc}(f; \mathcal{D}) \cdot (1 - \text{CR}(f; \mathcal{D}))
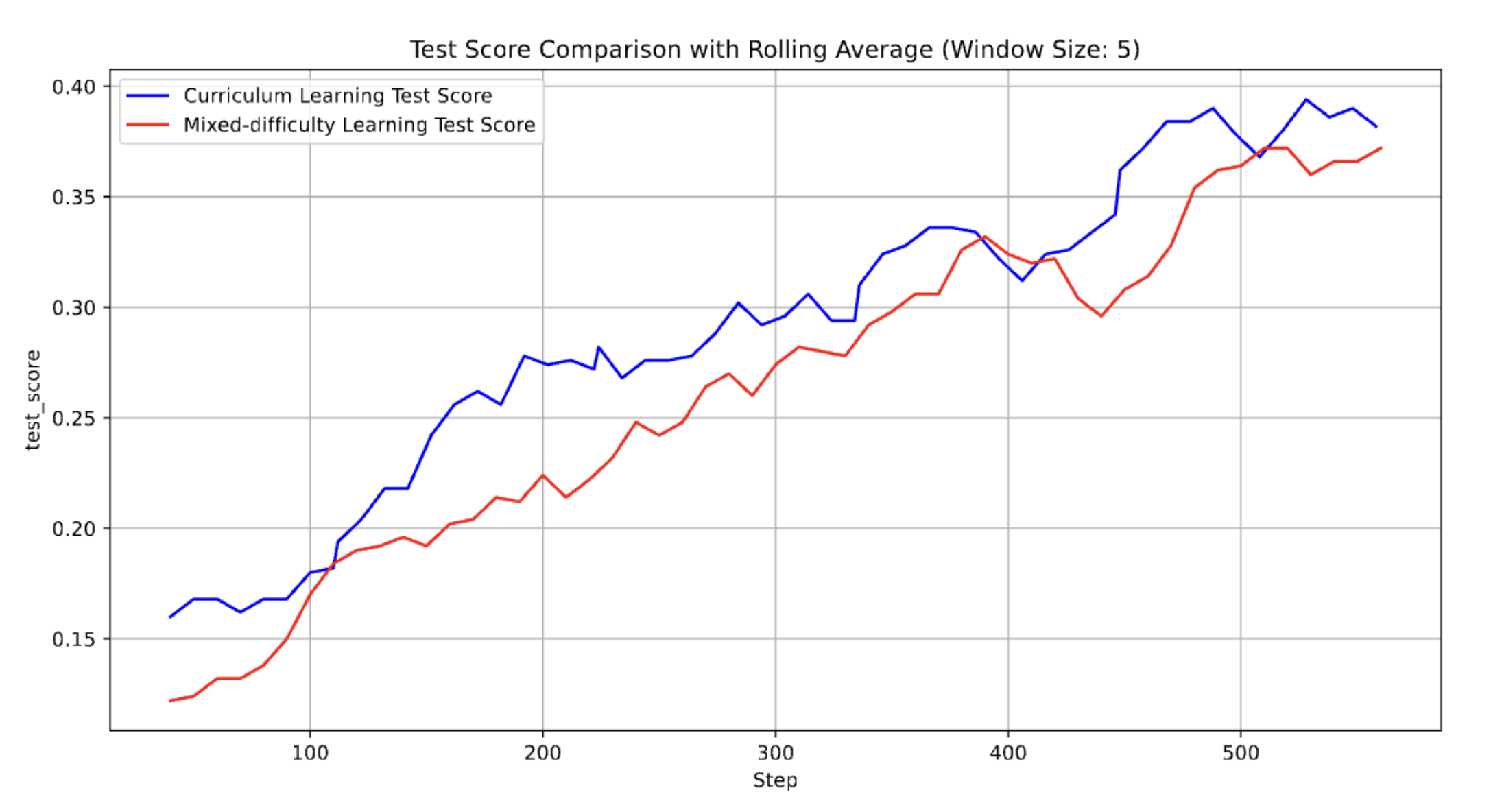
RQ-6: Effectiveness of Curriculum Learning
RQ-7: Longer Responses vs Reasoning Performance