Measure Theory in Machine Learning
Measure Theory Basics
Probability Space
(Ω, Σ, P)
- Probability Space:
- Set of all possible outcomes of probability experiments (or sample space)
- The state of partial knowledge about the outcome. (sigma-algebra)
- A measure on the space
Algebra
- A collection "F" is called algebra if:
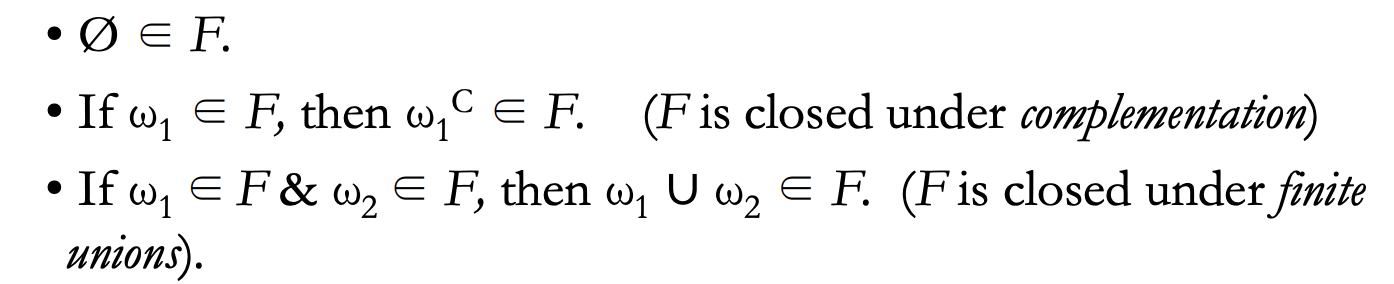
-Algebra
- A collection "F" is called sigma-algebra if:
- Example for {a, b, c}:
\sigma
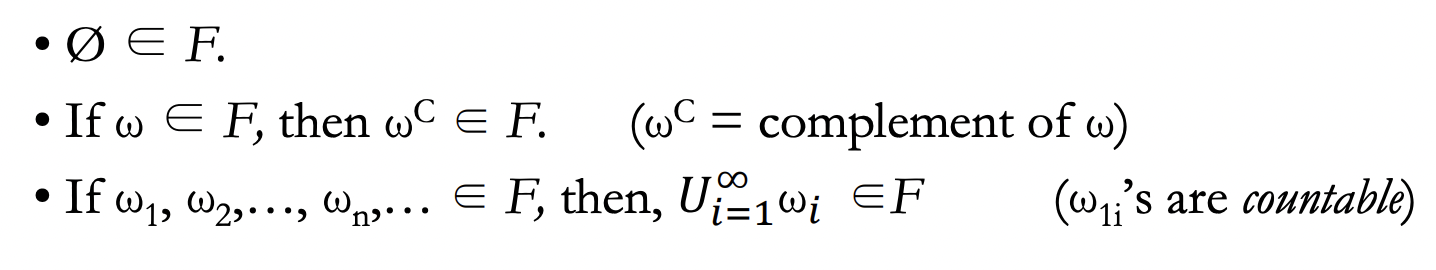
\{\{Φ\},\{a\},\{b\},\{c\},\{a,b\},\{b,c\},\{a,c\},\{a,b,c\}\}
-Algebra
- For a set "X", the intersection of all sigma-algebras "Ai" containing "X" is called the sigma-algebra generated by "X".
\sigma
\sigma(X) = \cap_{i=1}^n A_i \\
\{A_1, A_2, \cdots A_n\}: \text{All } \sigma-\text{algebras containing } X
Sample Space
- Set of all possible outcomes of the experiment we have.
- For instance: rolling a die with three sides of {a, b, c}.
- The sigma-algebra of the sample space is the set of all possible events from the experiments. (As an example, null is the event associated with not tossing the die!)
Topological Space
- A pair is called a topological space if:
- Here, is called a topology.
- Each element of a topology is called an open set.
(X, \tau)

\tau
Topological Space
- Examples:
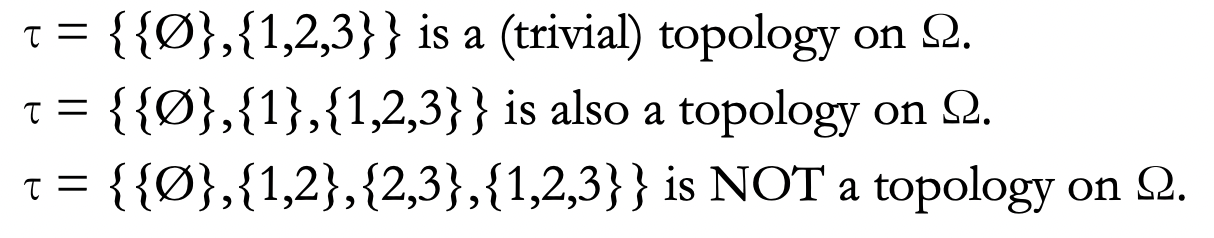
Borel sigma-algebra
- The borel -algebra of a topological space
denoted as is the sigma-algebra generated by the family of the open sets.
- The elements of are called the borel sets.
- Lemma: let , then
is the Borel field generated by the family of all open intervals C.
\sigma
B
B
C = \{(a; b): a < b\}
\sigma(C) = B_R
Measurable Space
- A pair is called a measurable space if X is a set and is Σ a non-empty sigma-algebra of X.
- A measurable space allows us to define a function that assigns real-numbered values to the abstract elements of Σ.
(X, \Sigma)
Measure
- Let (X, Σ) be a measurable space. A set function μ defined on Σ is called a measure iff:
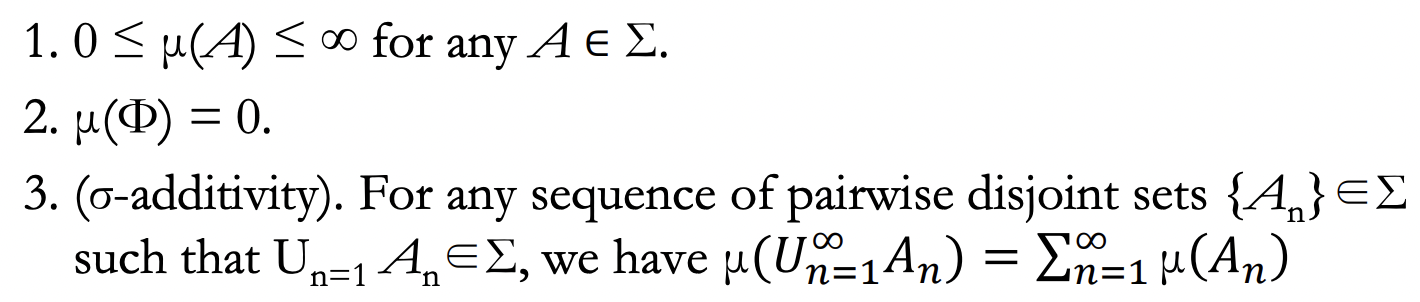
Measure
- A measure on a set, S, is a systematic way to assign a positive number to each suitable subset of that set, intuitively interpreted as its "size" (for the subset). In this sense, it generalizes the concepts of length, area, volume.
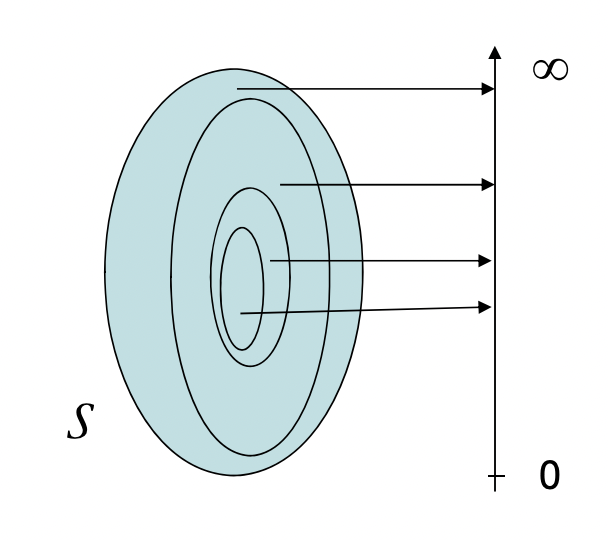
Measure space
- A triplet (X, Σ, μ) is a measure space if (X, Σ) is a measurable space and the μ is a measure such that:
- Note: if μ(X) = 1, then μ is a probability measure and the measurable space is a probability space.
\mu: \Sigma \rightarrow [0; \infty)
Lebesgue Measure
- There is a unique measure λ defined on
which satisfies:
- This is called the Lebesgue Measure. You can probably guess the Lebesgue measure for the set of real-numbers of higher dimensions!
\lambda([a, b]) = b-a
(R, B_R)
Measure Properties
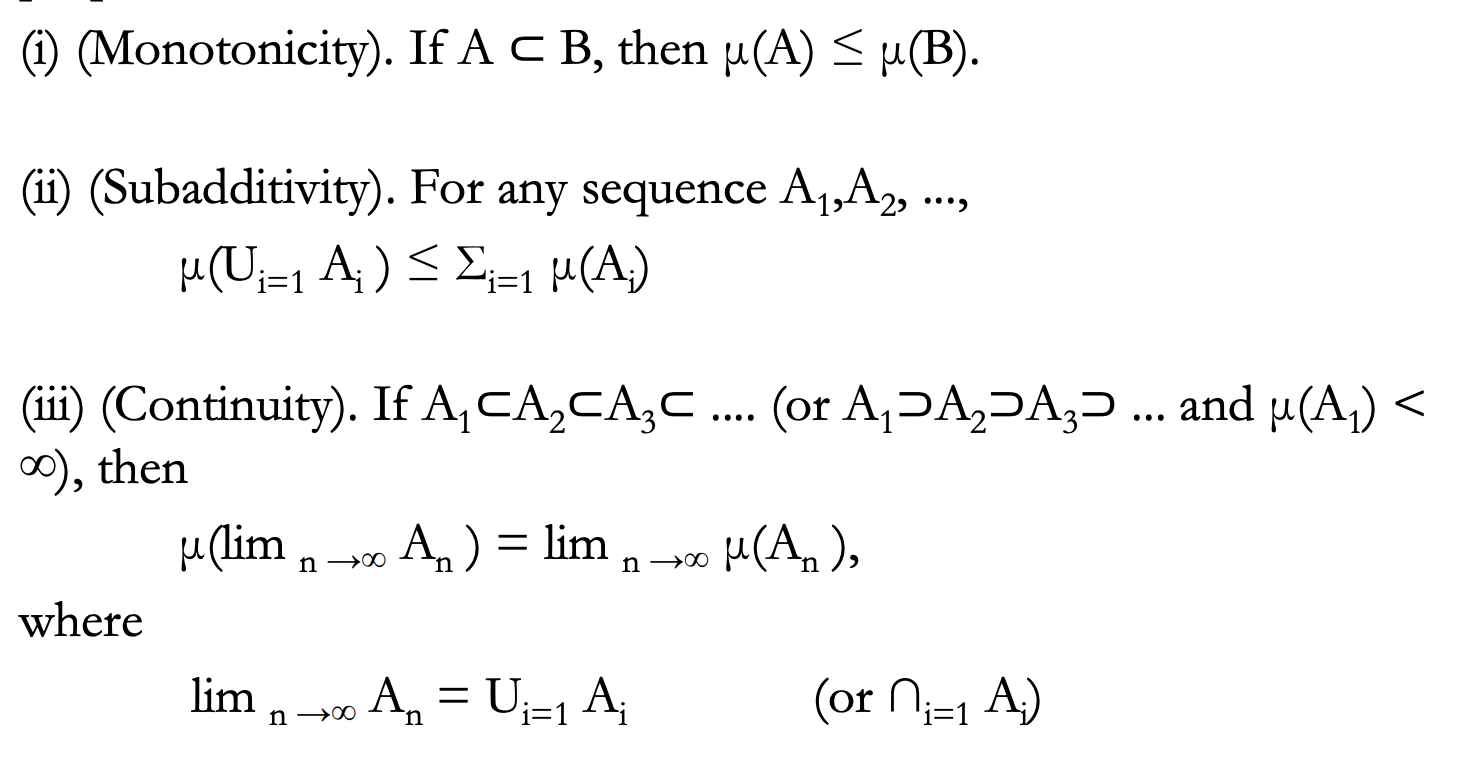
A measure theory application in machine learning
Analytical generalization bounds for ML models
- Paper:
Generalization in Machine Learning via Analytical Learning Theory
(Kawaguchi et al. 2019)
Screw Statistical Learning Theory!
- In SLT:
- Training datasets are random variables
- Generalization bounds are based on the family of all models learned on the dataset, not according to the specific dataset
- Pessimist generalizations.
- In this work:
- Analytical solutions for each problem!
- Analytical solutions for each problem!
Screw Statistical Learning Theory!
- Why treating each problem separately?
- Once a dataset is actually specified, there is no randomness remaining over the dataset.
- Thus, test errors can be small despite the large capacity of the hypothesis space and possible instability of the learning algorithm.
- Once a dataset is actually specified, there is no randomness remaining over the dataset.
Preliminaries
- Define the expected error of the model:
- Dataset:
- Emperical expected error:
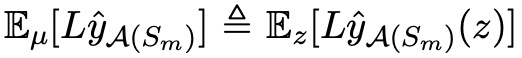
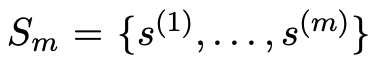
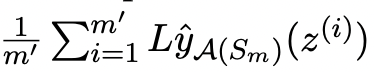
Preliminaries
- Generalization gap:
- Star-discrepancy
where Bt is a box for each in [0, 1].
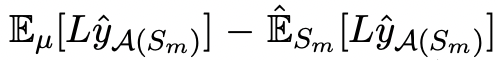
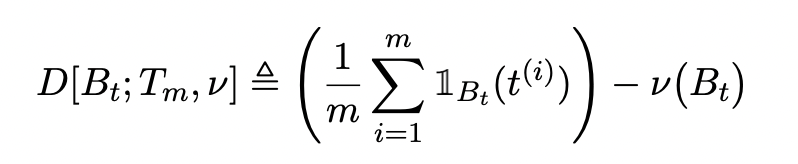
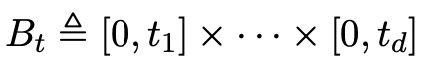
t_i
Preliminaries
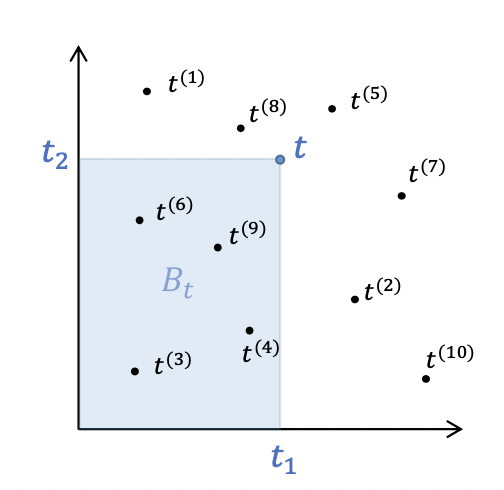
General Idea

General Idea

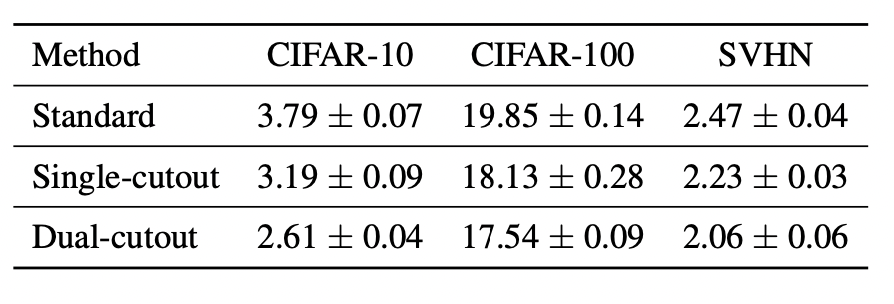
Dual Cutout Application
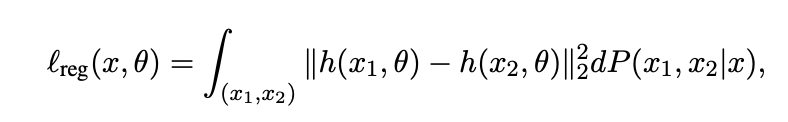
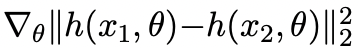
Dual Cutout Application