Making Look-Ahead Active Learning Strategies Feasible with Neural Tangent Kernels
Mohamad Amin Mohamadi
The University of British Columbia
NeurIPS 2022
Active Learning
Active learning: reducing the required amount of labelled data in training ML models through allowing the model to "actively request for annotation of specific datapoints".
We focus on Pool Based Active Learning:
x^* = \argmax_{x \in \mathcal{U}}{A \left(x, f_{\mathcal{L}}, \mathcal{L}, \mathcal{U}\right)}
f_{\mathcal{L}}
\mathcal{U}
\mathcal{L}
x^*
x
(x^*, y^*)
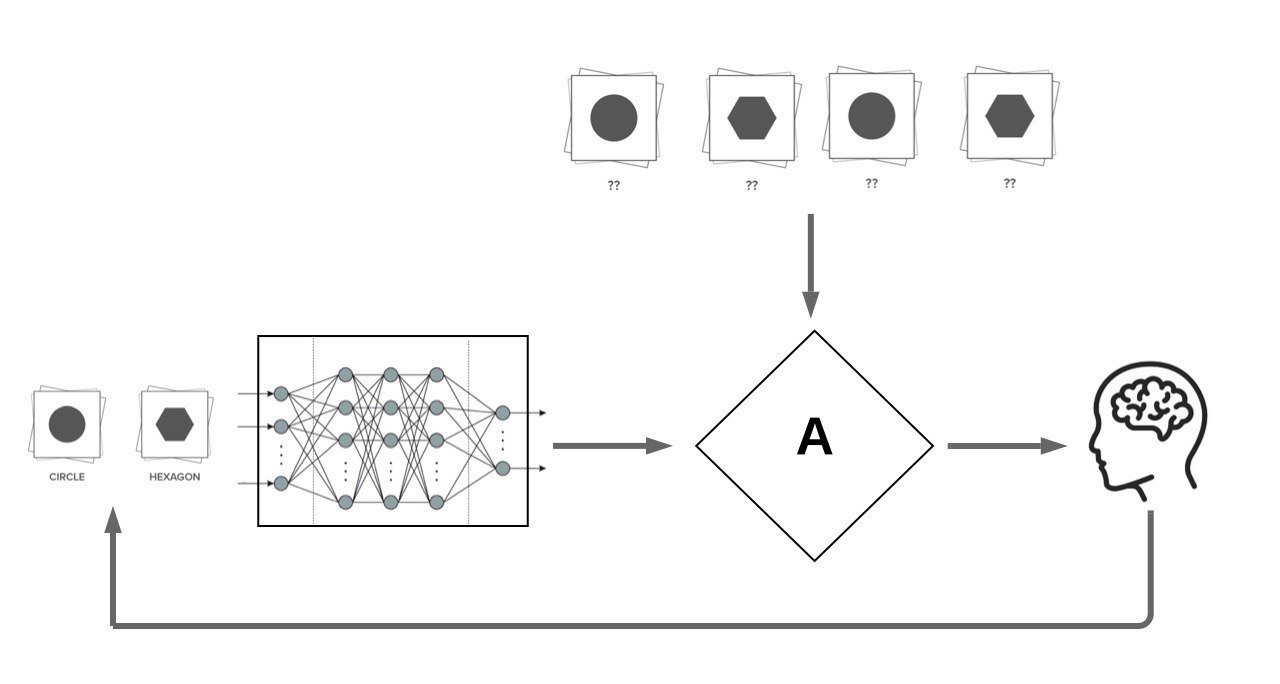
AL Acquisition Functions
Most proposed acquisition functions in deep active learning can be categorized to two branches:
- Uncertainty Based: Maximum Entropy, BALD
- Representation-Based: BADGE, LL4AL
Our Motivation: Making Look-Ahead acquisition functions feasible in deep active learning:
x
f_{\mathcal{L} \, \cup \, (x, \hat{y})}
\mathcal{L}
f_{\mathcal{L}}
x^*
(x^*, y^*)
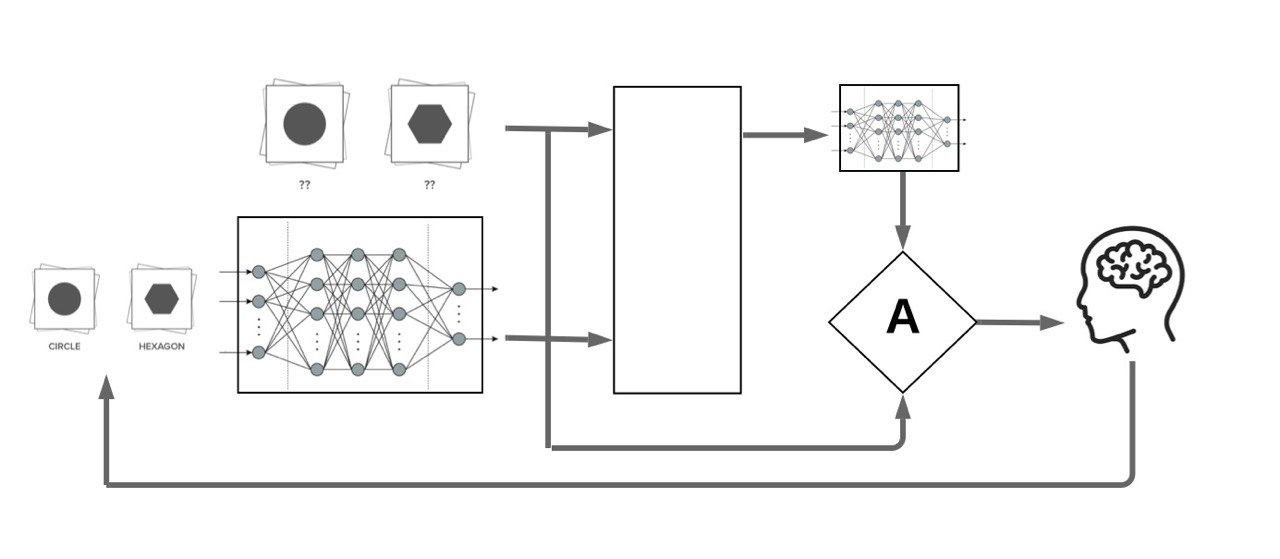
Retraining
Engine
\mathcal{U}
Contributions
-
Problem: Retraining the neural network with every unlabelled datapoint in the pool using SGD is practically infeasible.
-
Solution: We propose to use a proxy model based on the first-order Taylor expansion of the trained model to approximate this retraining.
-
Contributions:
- We prove that this approximation is asymptotically exact for ultra wide networks.
- Our method achieves similar or improved performance than best prior pool-based AL methods on several datasets.
-
Our proxy model can be used to perform fast Sequential Active Learning (no SGD needed)!
Approximation of Retraining
- Jacot et al.: training dynamics of suitably initialized infinitely wide neural networks can be captured by the Neural Tangent Kernels (NTKs).
f^\textit{lin}_{\mathcal{L}}(x) = \, f_0(x) + \Theta_0(x, \mathcal{X})
\, {\Theta_0(\mathcal{X}, \mathcal{X})}^{-1}
(\mathcal{Y} - f_0(\mathcal{X}))
- Lee et al.: the first-order Taylor expansion of a neural network around its initialization has training dynamics converging to that of the neural network as the width grows:
\Theta_0(x, y) \vcentcolon= \nabla_{\theta} f_{0}(x) \, \nabla_{\theta} f_{0}(y)^\top
\infty
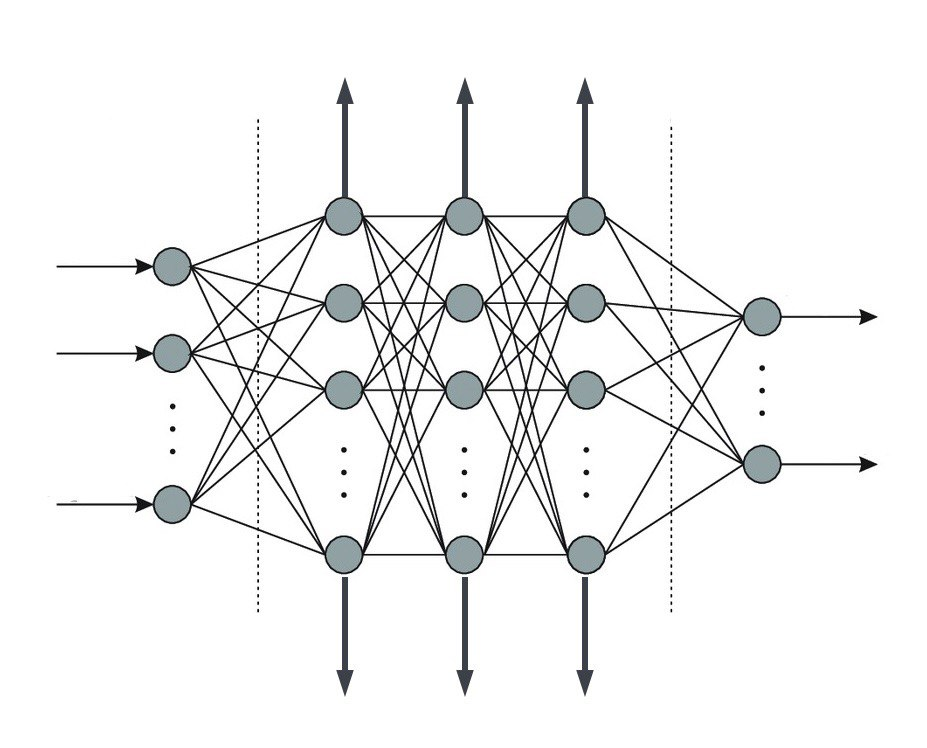
The Neural Tangent Kernel
- An important object in characterizing the training of suitably-initialized infinitely wide neural networks (NN)
- Describes the exact training dynamics of first-order Taylor expansion of any finite neural network:
- Is defined as
\Theta_f(x_1, x_2) = J_\theta f(x_1) {J_\theta f(x_2)}^\top
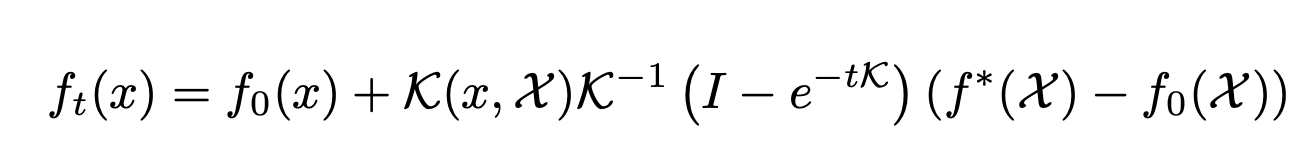
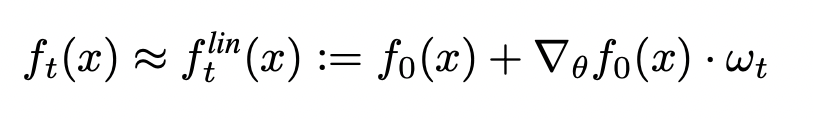
Training Neural Networks
\mathcal F: \{f: \mathbb{R}^{n_0} \to \mathbb{R}^{n_L}\}
\ell: \mathbb{R}^P \to \mathbb{R}
F^{(L)}: \mathbb{R}^P \to \mathcal{F}
p^{in} = \{(x_i, y_i)\}_i \text{ for } i \in [N]
Basic elements in neural network training:
Gradient Descent:
\nabla_\theta \ell(\theta_t) = - \sum_{i=1}^N (f_{\theta_t}(x_i) - y_i) \frac{\partial f_{\theta_t} (x_i)}{\partial \theta}
Training Neural Networks
Idea: Study neural networks in the function space!
Gradient Flow:
\frac{\partial \theta(t)}{\partial t} = - \sum_{i=1}^N (f_{\theta(t)}(x_i) - y_i) \frac{\partial f_{\theta(t)} (x_i)}{\partial \theta}
Change in the function output:
\frac{\partial f_{\theta(t)} (x_i)}{\partial t} = \frac{\partial f_{\theta(t)} (x_i)}{\partial \theta} \frac{\theta(t)}{\partial t}
= -\sum_{j=1}^N (f_{\theta(t)}(x_j) - y_j) \langle \frac{\partial f_{\theta(t)} (x_i)}{\partial \theta}, \frac{\partial f_{\theta(t)} (x_j)}{\partial \theta} \rangle
Hmm, looks like we have a kernel on the right hand side!
Training Neural Networks
\frac{\partial f_{\theta(t)} (x_i)}{\partial t} = -\sum_{j=1}^N (f_{\theta(t)}(x_j) - y_j) K_{\theta(t)}(x_i, x_j)
So:
K_{\theta(t)}(x_i, x_j) = \langle \frac{\partial f_{\theta(t)} (x_i)}{\partial \theta}, \frac{\partial f_{\theta(t)} (x_j)}{\partial \theta} \rangle
where
this is called the Neural Tangent Kernel!
\Longrightarrow f_{\theta(t)}(x) = \underbrace{\sum_{j=1}^N K_{\theta(t)}(x, x_j) f_{\theta(t)}(x_j)}_\text{function of $f_{\theta(t)}(x), x$ at $t$} - \underbrace{\sum_{j=1}^N K_{\theta(t)}(x, x_j) f^*(x_j)}_\text{function of $x$ at $t$}
- Idea: approximate the retrained neural network on a new datapoint ( ) using the first-order taylor expansion of the network around the current model.
f_{\mathcal{L} \, \cup \, (x, \hat{y})}
f_{\mathcal{L}}
f_{\mathcal{L}^+}(x)
\approx f^\textit{lin}_{\mathcal{L}^+}(x)
=
f_\mathcal{L}(x) + \Theta_{\mathcal{L}}(x, {\color{blue}{\mathcal{X}}}^{\color{orange}{+}}){\Theta_{\mathcal{L}}({\color{blue}{\mathcal{X}}}^{\color{orange}{+}}, {\color{blue}{\mathcal{X}}}^{\color{orange}{+}})}^{-1} \left (\mathcal{Y}^+ - f_\mathcal{L}(\mathcal{X}^+) \right )
+
-1
-
(
)
\times
f^\textit{lin}_{\mathcal{L}^+}(x) =
- We prove that this approximation is asymptotically exact for ultra wide networks and is empirically comparable to SGD for finite width networks.
Approximation of Retraining
- Idea: approximate the retrained neural network on a new datapoint ( ) using the first-order taylor expansion of the network around the current model .
f_{\mathcal{L} \, \cup \, (x, \hat{y})}
f_{\mathcal{L}}
f_{\mathcal{L}}
f_{\mathcal{L}^+}(x)
\approx f^\textit{lin}_{\mathcal{L}^+}(x)
=
f_\mathcal{L}(x) + \Theta_{\mathcal{L}}(x, {\color{blue}{\mathcal{X}}}^{\color{orange}{+}}){\Theta_{\mathcal{L}}({\color{blue}{\mathcal{X}}}^{\color{orange}{+}}, {\color{blue}{\mathcal{X}}}^{\color{orange}{+}})}^{-1} \left (\mathcal{Y}^+ - f_\mathcal{L}(\mathcal{X}^+) \right )
+
-1
-
(
\times
f^\textit{lin}_{\mathcal{L}^+}(x) =
- We prove that this approximation is asymptotically exact for ultra wide networks and is empirically comparable to SGD for finite width networks.
Approximation of Retraining
Look-Ahead Active Learning
- We employ the proposed retraining approximation in a well-suited acquisition function which we call the Most Likely Model Output Change (MLMOC):
A_\textit{MLMOC}(x', f_{\mathcal L}, \mathcal{L}_t,\, \mathcal{U}_t)
\vcentcolon=
\sum_{x \in \mathcal{U}} \lVert f_{\mathcal L}(x) - f^\textit{lin}_{\mathcal L^+}(x)) \rVert_2
-
Although our experiments in the pool-based AL setup were all done using MLMOC, the proposed retraining approximation is general.
- We hope that this enables new directions in deep active learning using the look-ahead criteria.
Experiments
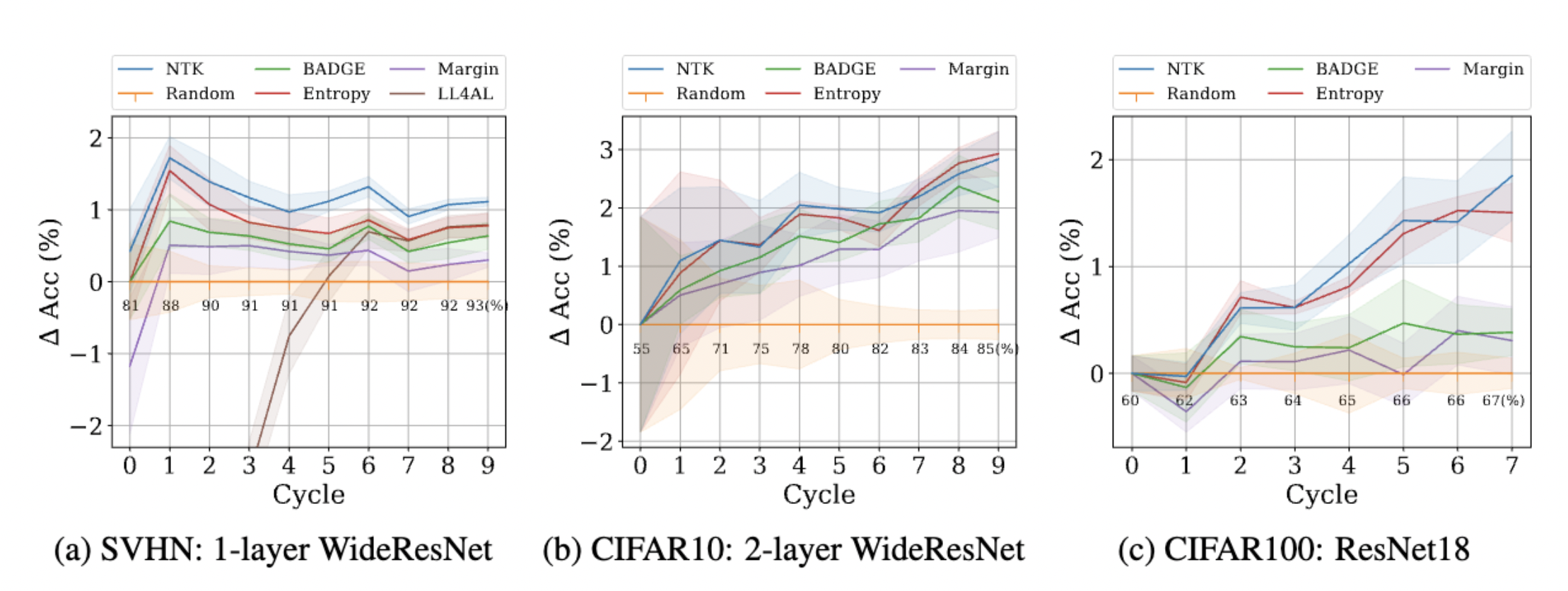
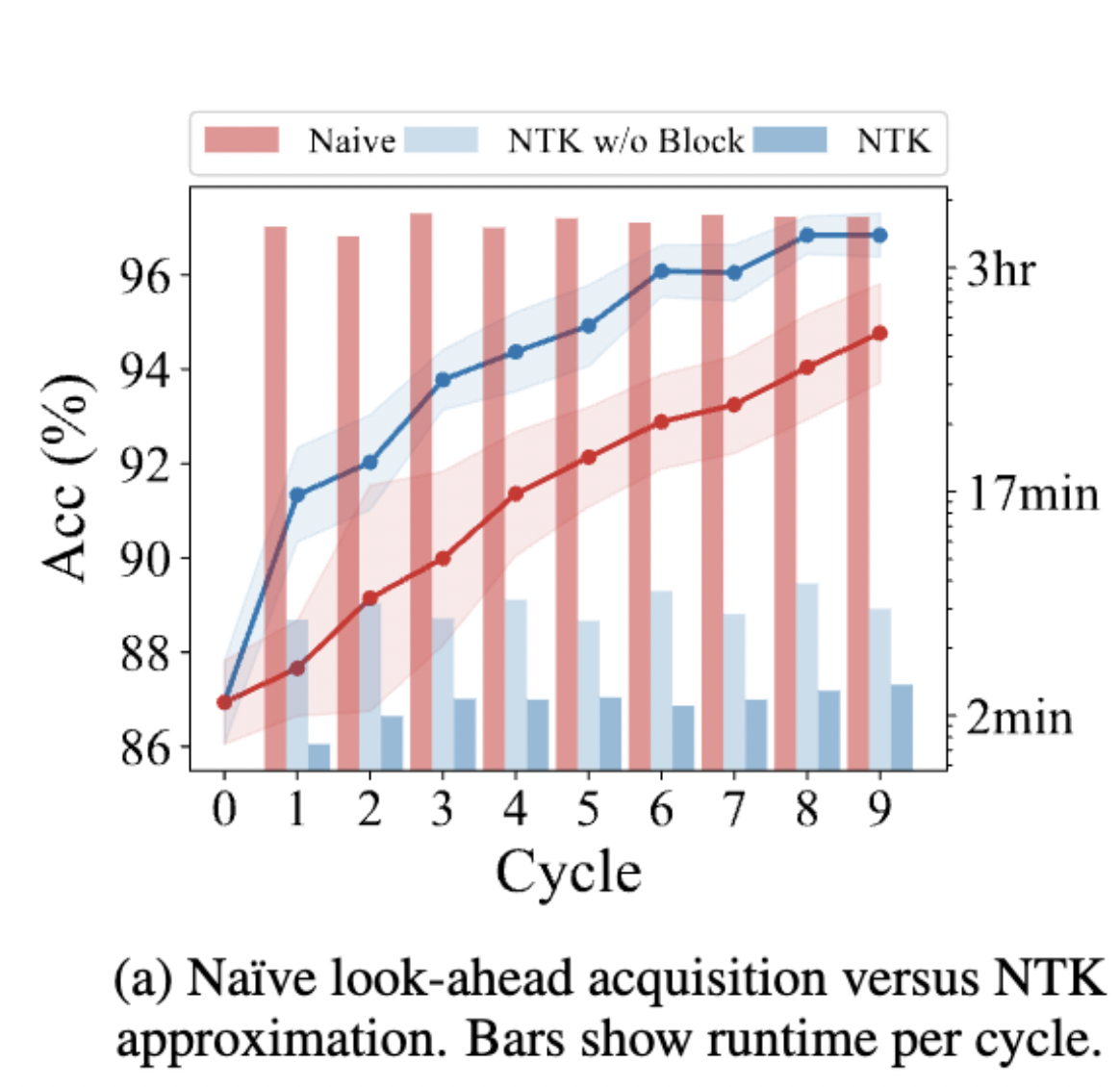
Retraining Time: The proposed retraining approximation is much faster than SGD.
Experiments: The proposed querying strategy attains similar or better performance than best prior pool-based AL methods on several datasets.
Thanks!
arXiv URL
GitHub URL