Machine Learning Foundations
Week 9: Revision
Theorem
Goal : \(\min \limits_x f(x)\)
Let \(f\) be a differentiable and convex function from \(\mathbb R^d \rightarrow \mathbb R\), \(x^* \in \mathbb R^d\) is a global minimum of \(f\) if and only if \(\nabla f(x^*) = 0\).
Necessary and sufficient conditions for optimality of convex functions
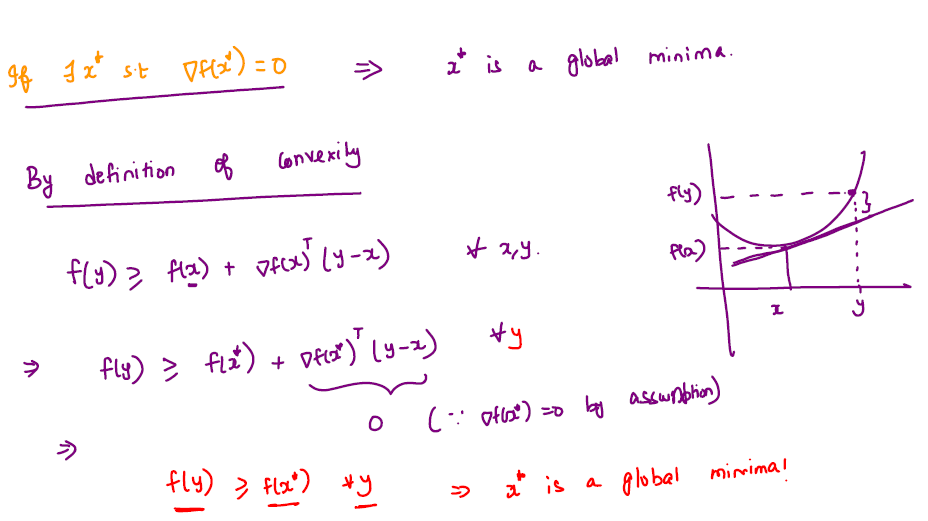
Additional Properties of Convex Functions
If \( f: \mathbb{R}^d \rightarrow \mathbb{R}, g: \mathbb{R}^d \rightarrow \mathbb{R}\) are both convex functions, then \( f(x) + g(x)\) is a convex function
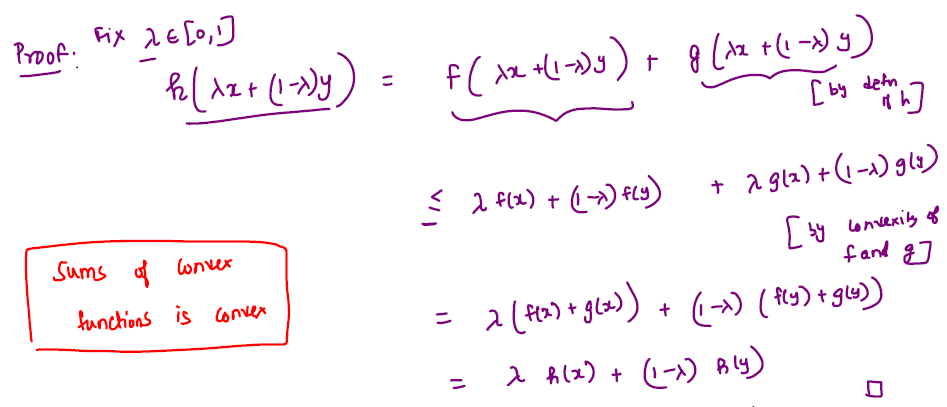
https://katex.org/docs/supported.html
Additional Properties of Convex Functions
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) is a convex and non-decreasing function and \(g: \mathbb{R}^d \rightarrow \mathbb{R}\) be a convex function, then their composition \(h = f(g(x))\) is also a convex function.
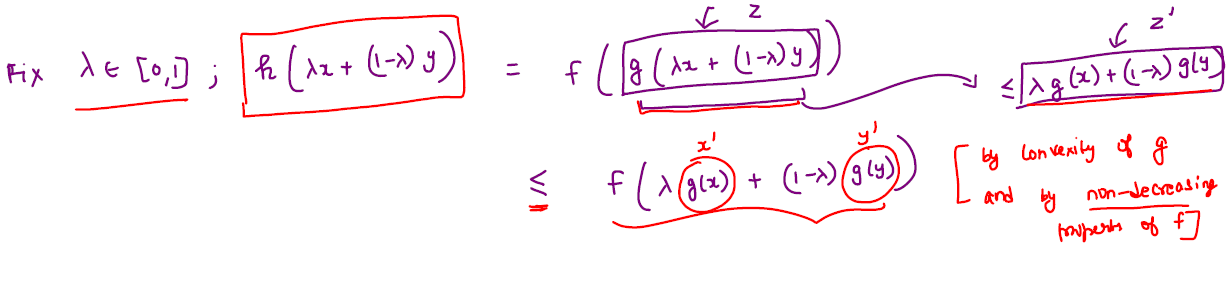
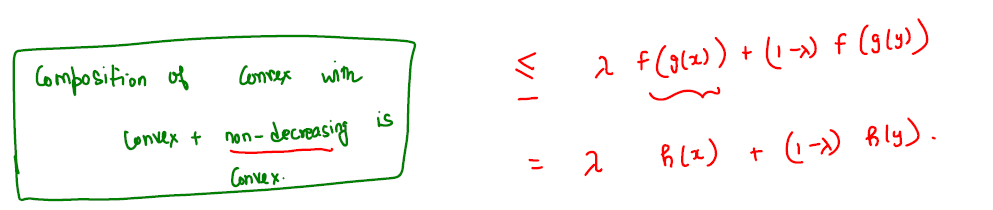
Additional Properties of Convex Functions
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) is a convex function and \(g: \mathbb{R}^d \rightarrow \mathbb{R}\) be a linear function, then their composition \( h = f(g(x))\) is also a convex function.
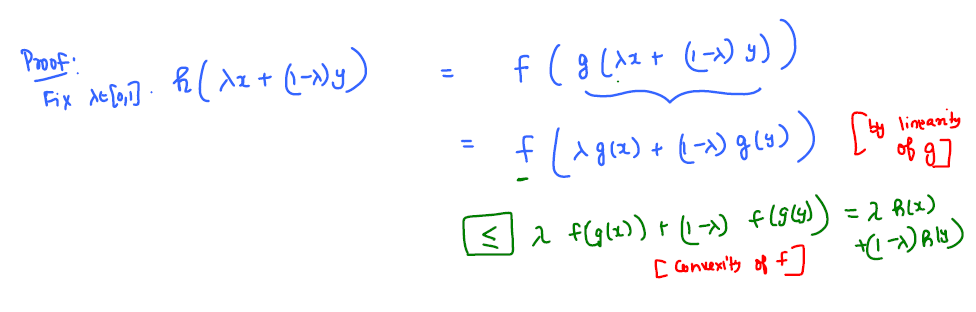
Additional Properties of Convex Functions
In general, if \(f\) and \(g\) are both convex functions, then \(h=fog\) may not be convex function.
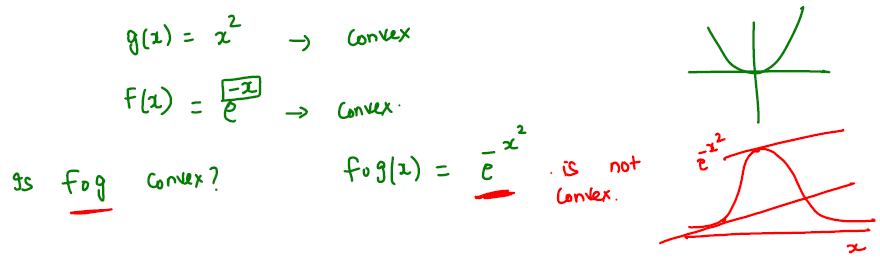
Note: \(g\) is concave if and only if \(f=-g\) is convex.
Applications of Optimization in ML
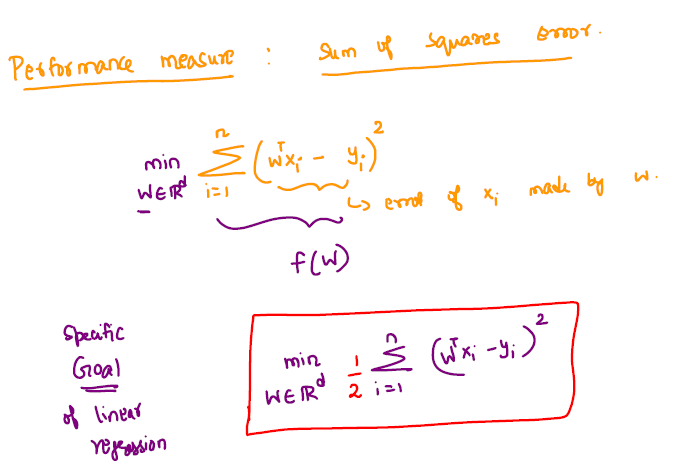
Linear Regression:
Training data \(\rightarrow\) \({X_1,X_2,...,X_n}\) with corresponding outputs \({y_1,y_2,...,y_n}\), where \(X_i \in \mathbb R^d \) and \( y_i \in \mathbb R \), \( \forall i \).
Gradient of the sum of squares error
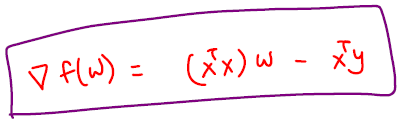
Analytical or closed form solution of coefficients \(w^*\) of a linear regression model
Applications of Optimization in ML
In linear regression, the gradient descent approach avoids the inverse computation by iteratively updating the weights.
Stochastic gradient descent:
- Computes approximation of gradient to make gradient computation faster (because in GD \(X^TX\) will use entire dataset).
- Samples a small set of data points at random for every iteration to compute the gradient.
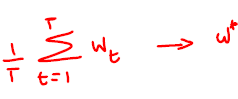
Constrained Optimization
Consider the constrained optimization problem as follows:
Lagrangian function:
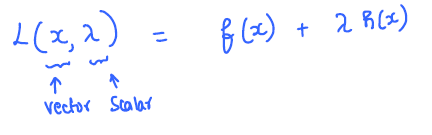
Constrained Optimization
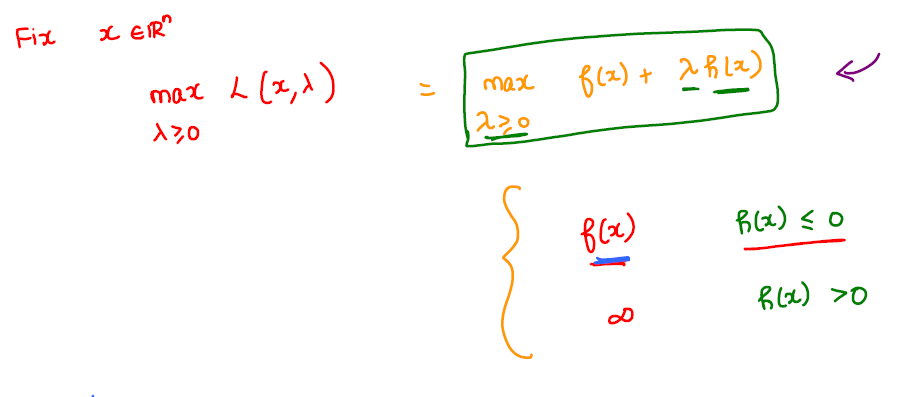
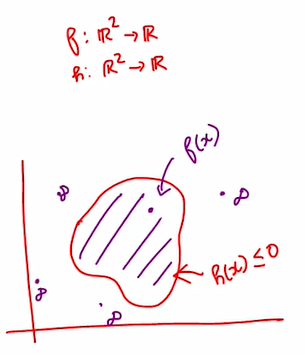
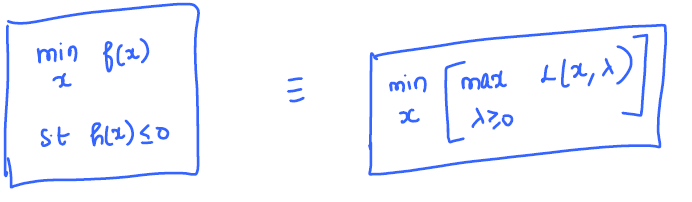
Note: depending upon if \(x\) is inside or outside the constrained set, we will get the objective value to be \(f(x)\) or \(\inf\).
Primal and dual problem
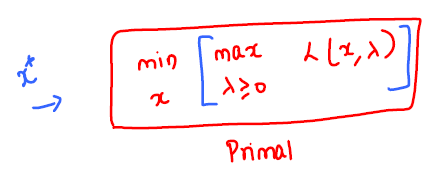
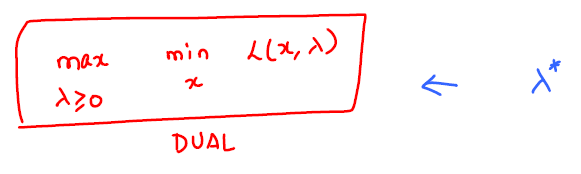
| Weak Duality | Strong Duality |
|---|---|
|
|
If f and g are convex functions. |
Karush-Kuhn-Tucker Conditions
Consider the optimization problem with multiple equality and inequality constraints as follows:
The Lagrangian function is expressed as follows:
Karush-Kuhn-Tucker Conditions:
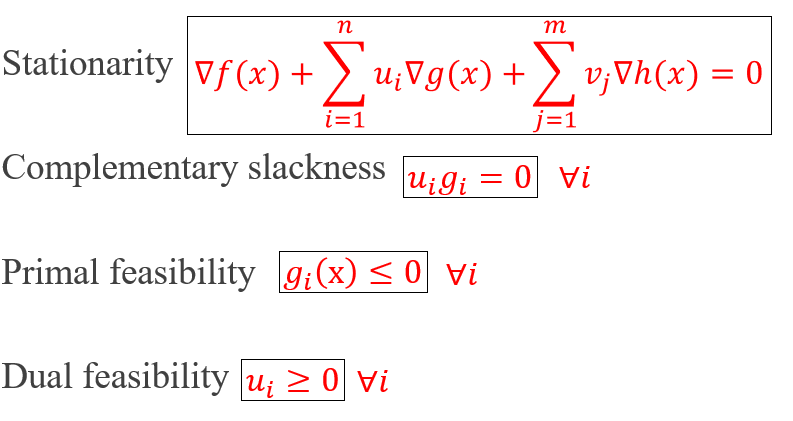
Example:
minimize
\(f(x) = 2(x_1+1)^2 + 2(x_2-4)^2\)
subject to
\(x_1^2+x_2^2 \le 9\)
\(x_1+x_2 \ge 2\)