Mass mapping and cosmological inference with higher-order statistics

Andreas Tersenov

ARGOS-TITAN-TOSCA workshop, July 8, 2025

Why this presentation may not be the best

Weak Lensing - Relation between

\kappa \,\, \mathrm{and} \,\, \gamma

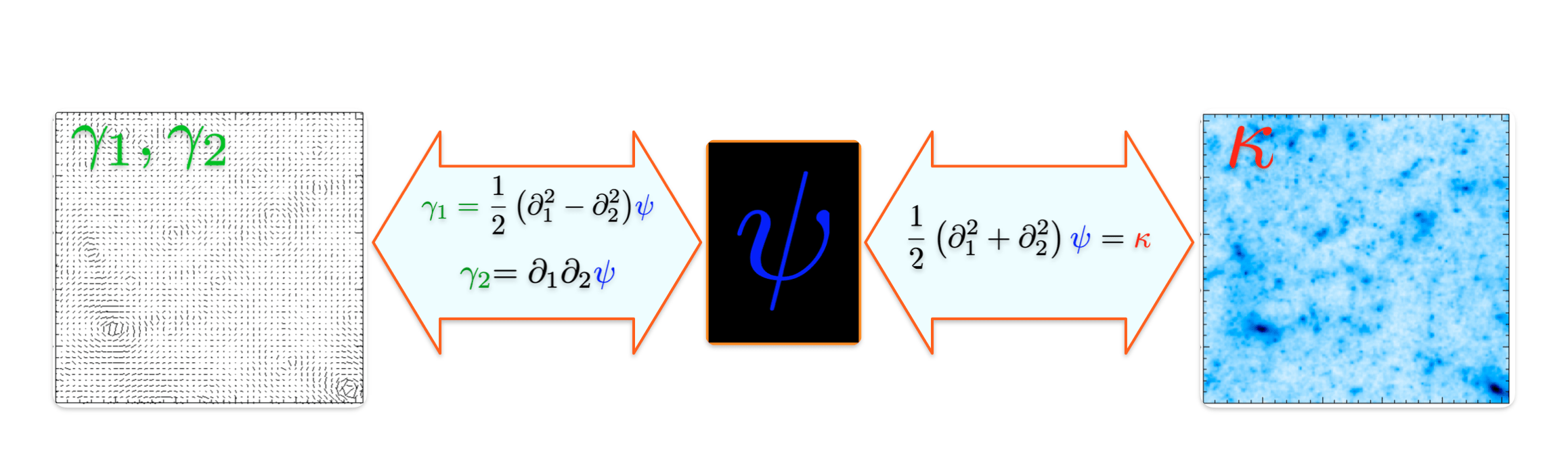
From convergence to shear:
From shear to convergence:

\gamma_i = \hat{P}_i \kappa

\kappa = \hat{P}_1 \gamma_1 + \hat{P}_2 \gamma_2

\hat{P}_1(k)=\dfrac{k_1^2 - k_2^2}{k^2}, \,\, \hat{P}_2(k)=\dfrac{2k_1k_2}{k^2}

In practice...

Shear measurements are discrete, noisy, and irregularly sampled
We actually measure the reduced shear
Masks and integration over a subset of ℝ2 lead to border errors ⇒ missing data problem
Convergence is recoverable up to a constant ⇒ mass-sheet degeneracy problem

Mass mapping is an ill-posed inverse problem

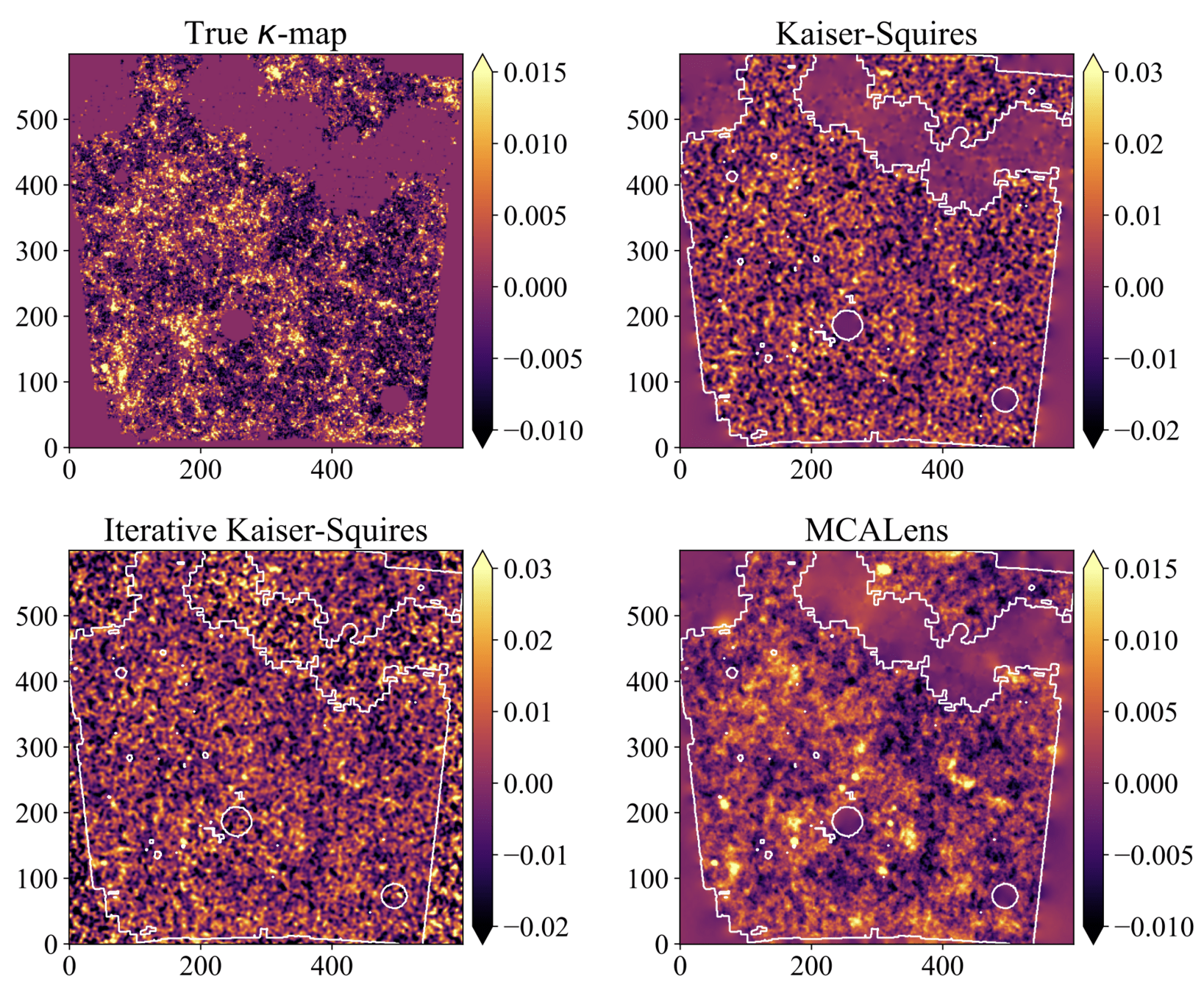
Different algorithms have been introduced, with different reconstruction fidelities, in terms of RMSE

Motivating this project:

The various algorithms have different RMSE performance
In cosmology we don't care about RMSE of mass maps, but only about the resulting cosmological parameters

⇒ This should be our final benchmark!

So... does the choice of the mass-mapping algorithm have an impact on the final inferred cosmological parameters?

Or as long as you apply the same method to both observations and simulations it won't matter?

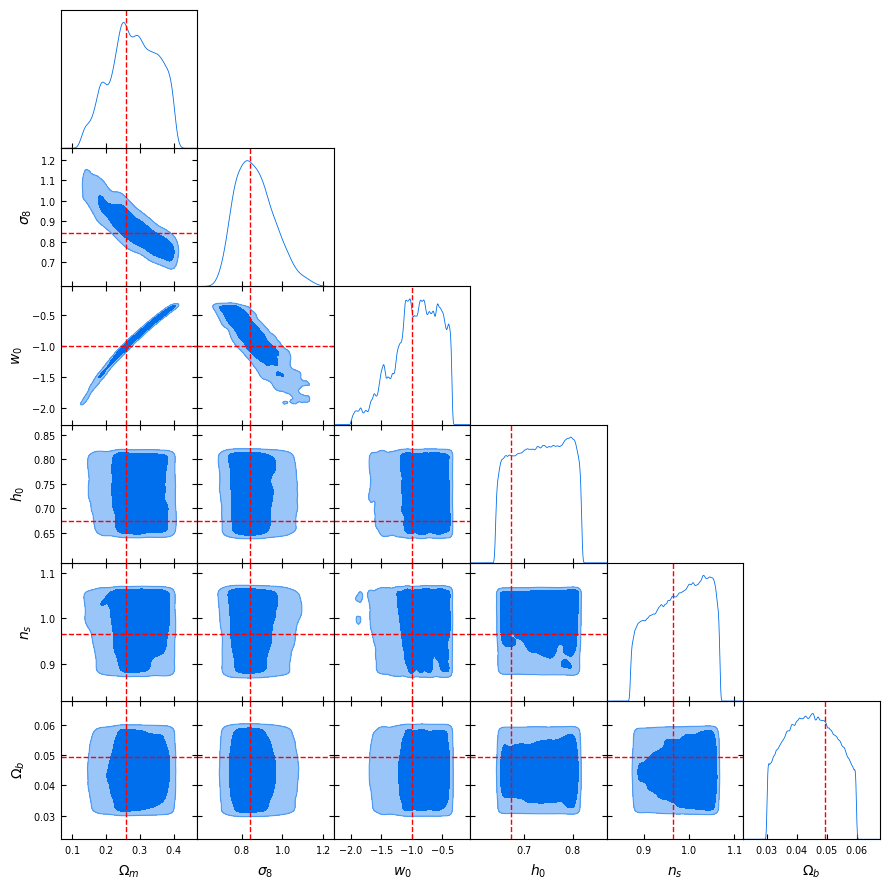
cosmoSLICS mass maps

\begin{array}{ll} \hline \hline \text{Method} & \text{RMSE} \downarrow \\ \hline \text{KS } & 1.1 \times 10^{-2} \\ \text{iKS } & 1.1 \times 10^{-2} \\ \text{MCALens} & 9.8 \times 10^{-3} \\ \hline \end{array}

For which we have/assume an analytical likelihood function

t = f(x)

How to constrain cosmological parameters?

Likelihood → connects our compressed observations to the cosmological parameters

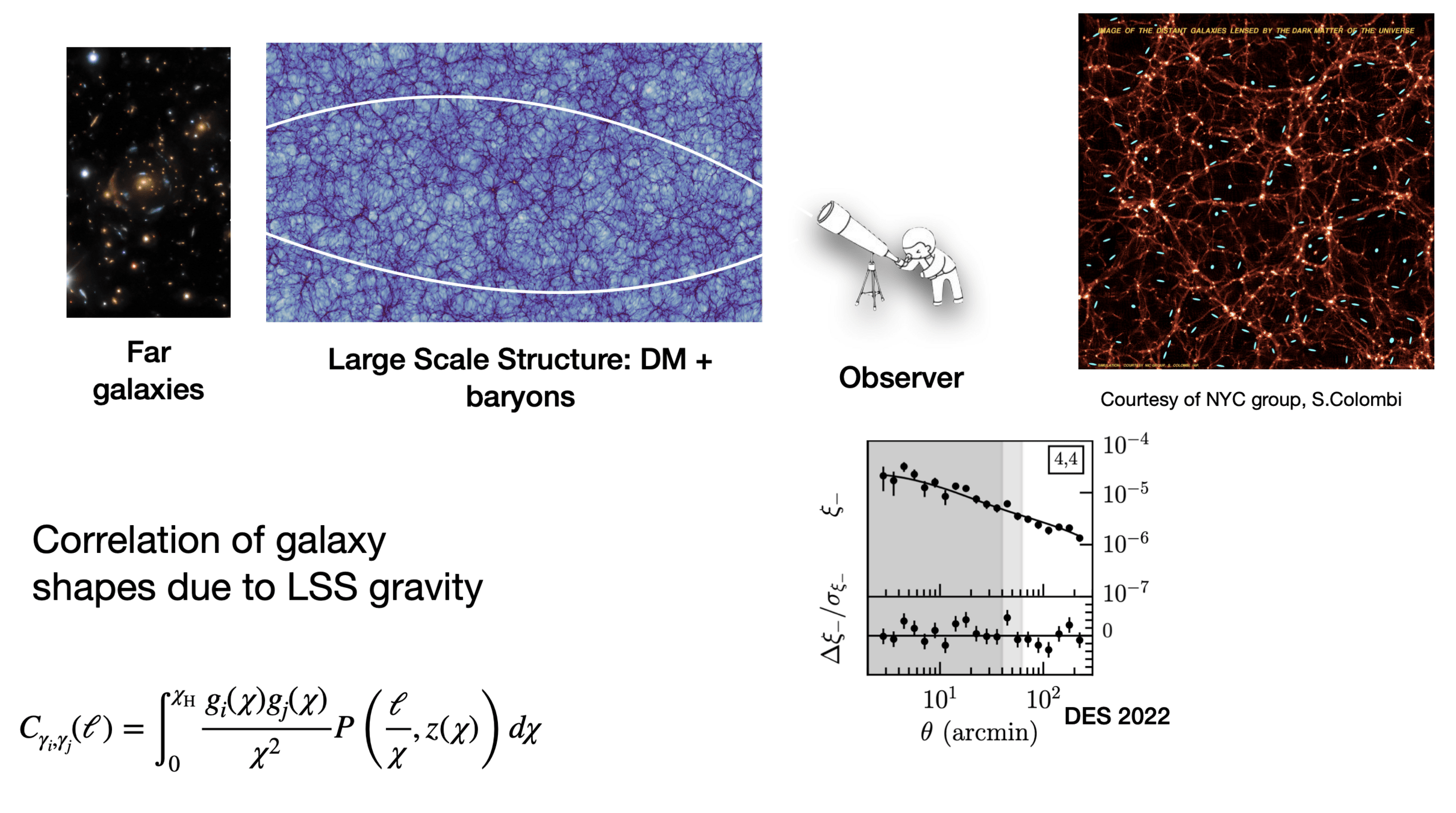
\underbrace{p\left(\theta \mid t=t_0\right)}_{\text {posterior }} \propto \underbrace{p\left(t=t_0 \mid \theta\right)}_{\text {likelihood }} \underbrace{p(\theta)}_{\text {prior }}

p\left(t=t_0 \mid \theta\right)

2pt vs higher-order statistics

The traditional way of constraining cosmological parameters misses the non-Gaussian information in the field.

t = f(x)

DES Y3 Results

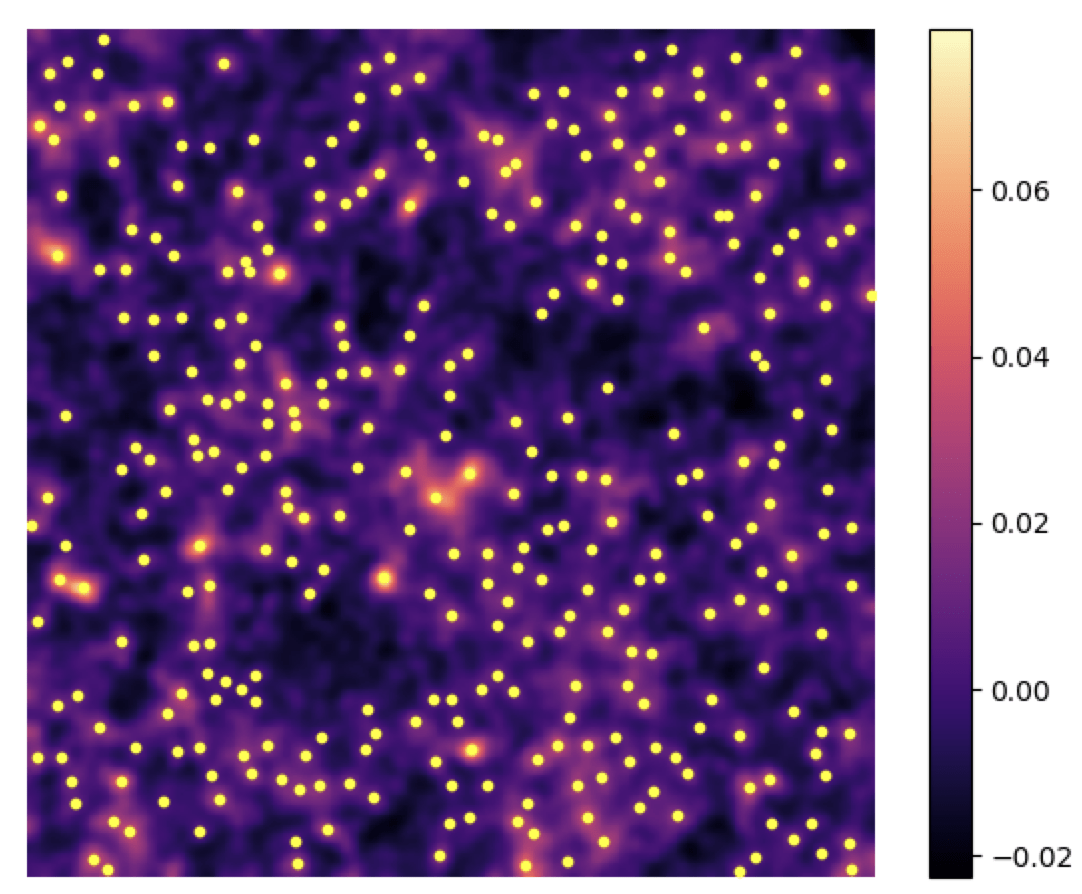
Higher Order Statistics: Peak Counts

Peaks: local maxima of the SNR field
Peaks trace regions where the value of 𝜅 is high → they are associated to massive structures

Multi-scale (wavelet) peak counts

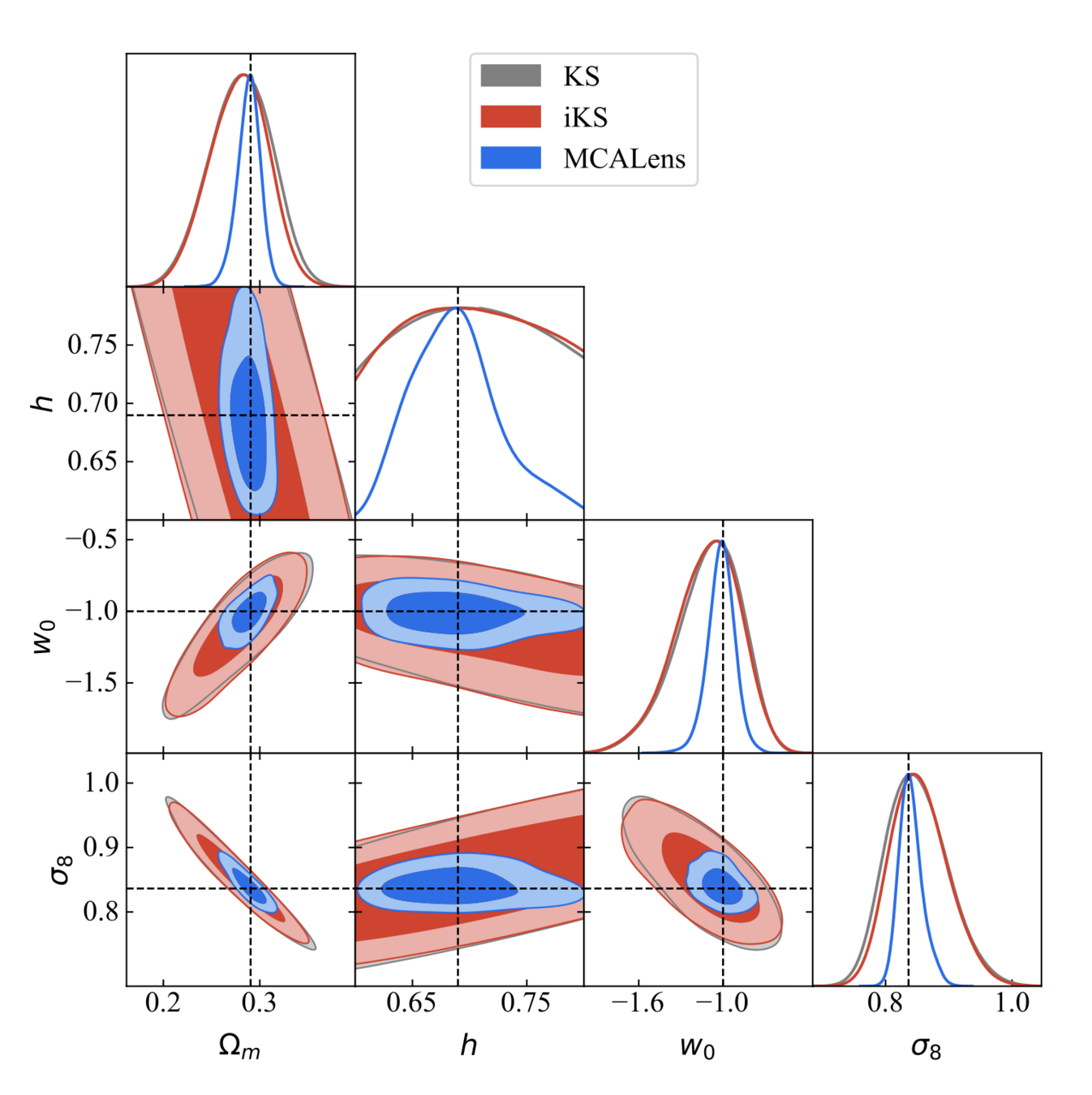
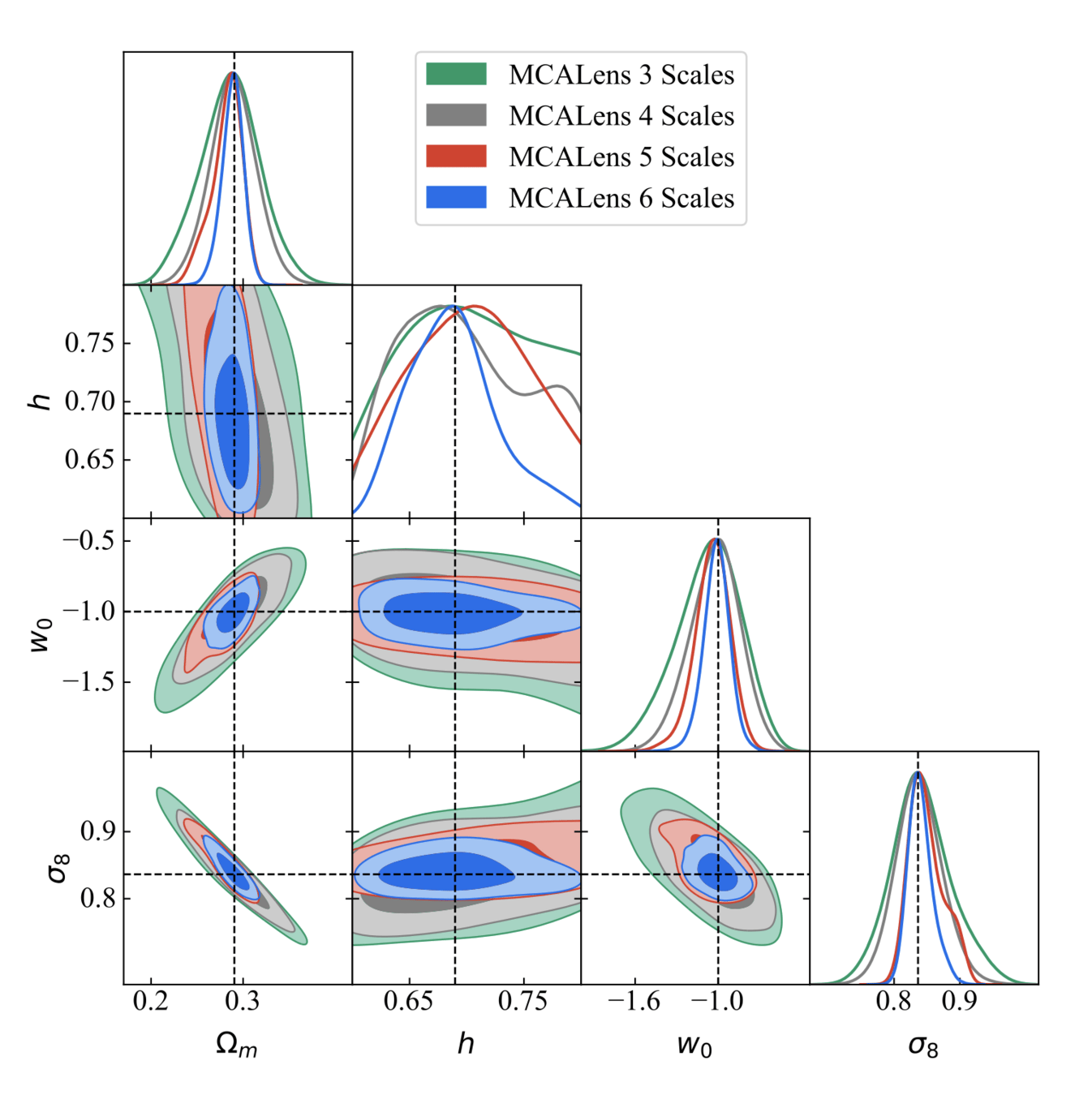
Results

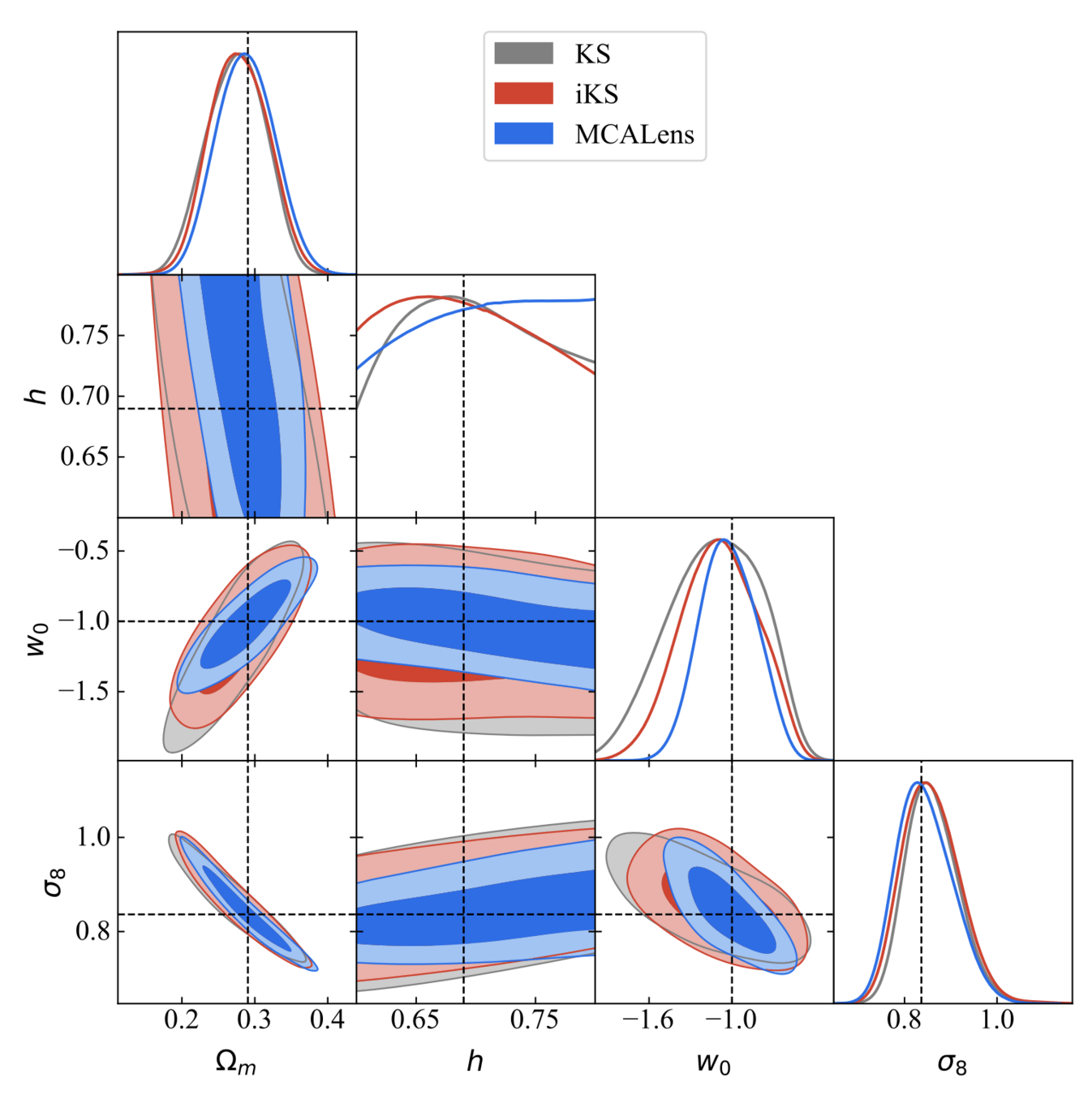
Mono-scale peaks

Multi-scale peaks

Where does this improvement come from?

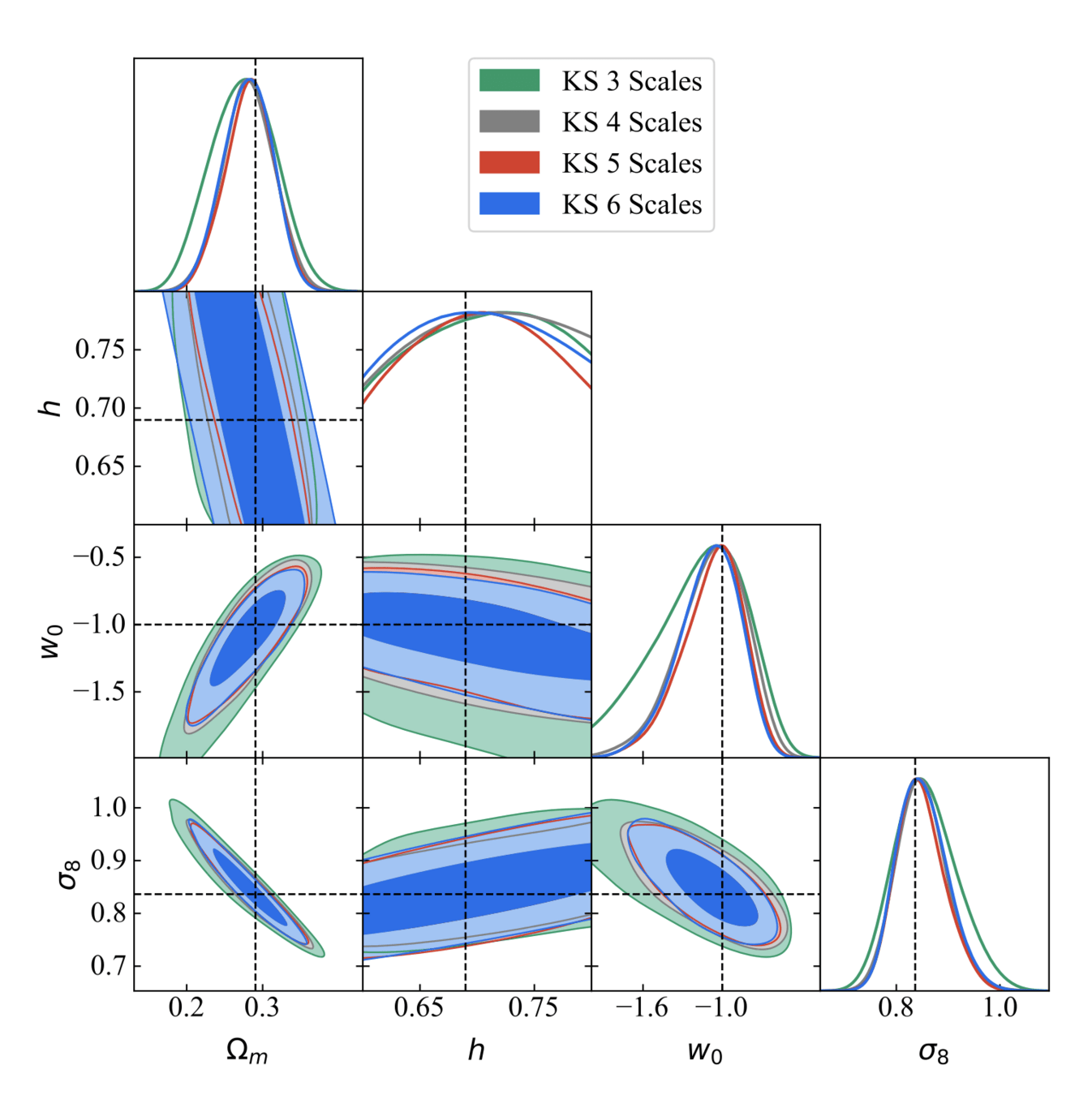
Kaiser-Squires

MCALens

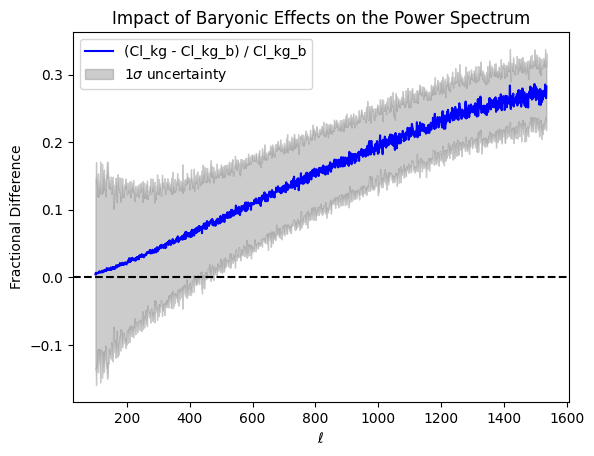
Baryonic effects

Effects that stem from astrophysical processes involving ordinary matter (gas cooling, star formation, AGN feedback)
They modify the matter distribution by redistributing gas and stars within halos.

Suppress matter clustering on small scales
Depend on the cosmic baryon fraction and cosmological parameters.
Must be modeled/marginalized over to avoid biases in cosmological inferences from WL.

Baryonic impact on LSS statistics

baryonic effects in P(k)

Credit: Giovanni Aricò

Project: Testing impact baryonic effects on WL HOS

Idea - Explore two things:

Information content of summary statistics as a function of scale cuts
Testing the impact of baryonic effects on posterior contours

This will show:

On what range of scales can the different statistics be used without explicit model for baryons
Answer the question: how much extra information beyond the PS these statistics can access in practice

cosmoGRID simulations

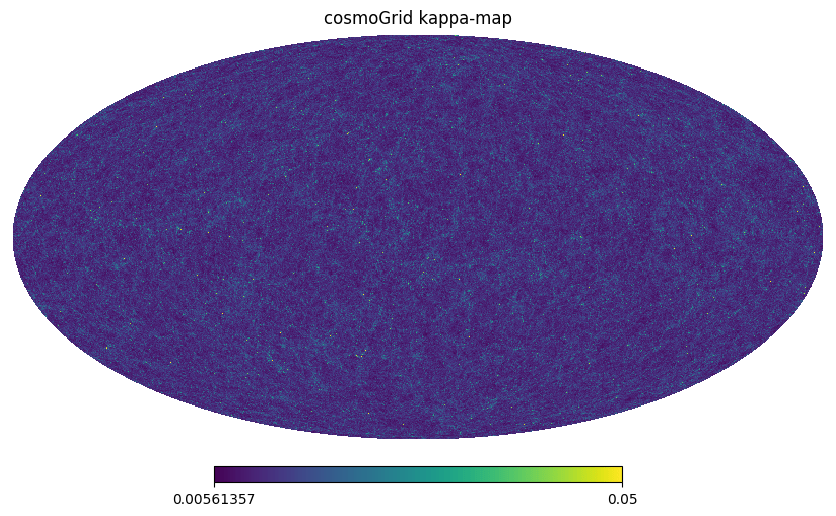
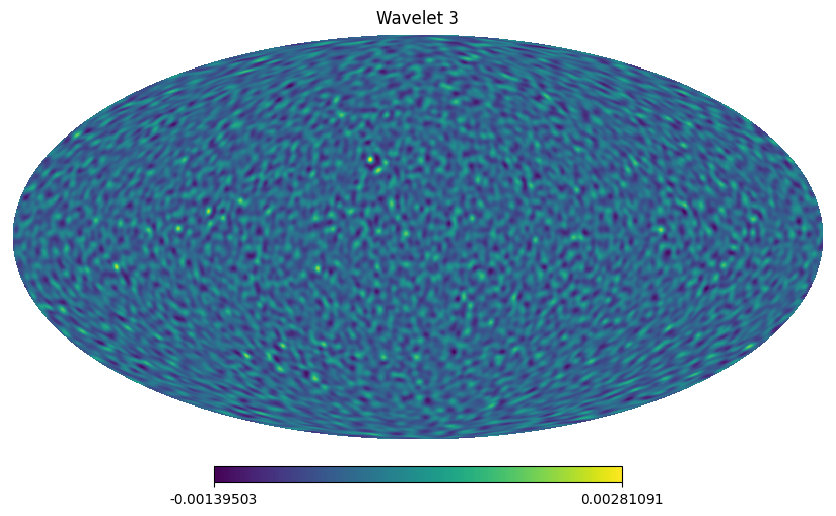
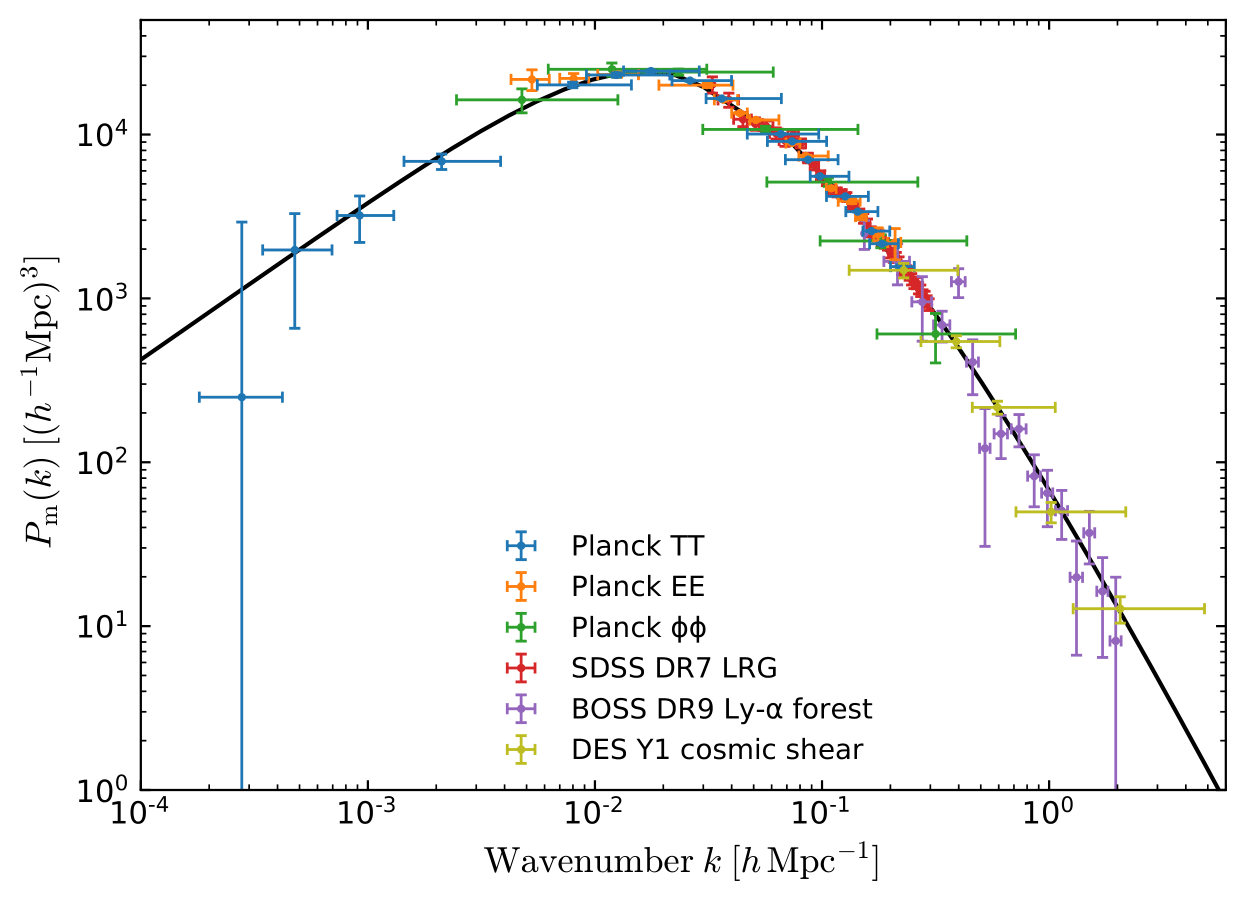
Power Spectrum

Wavelet l1-norm

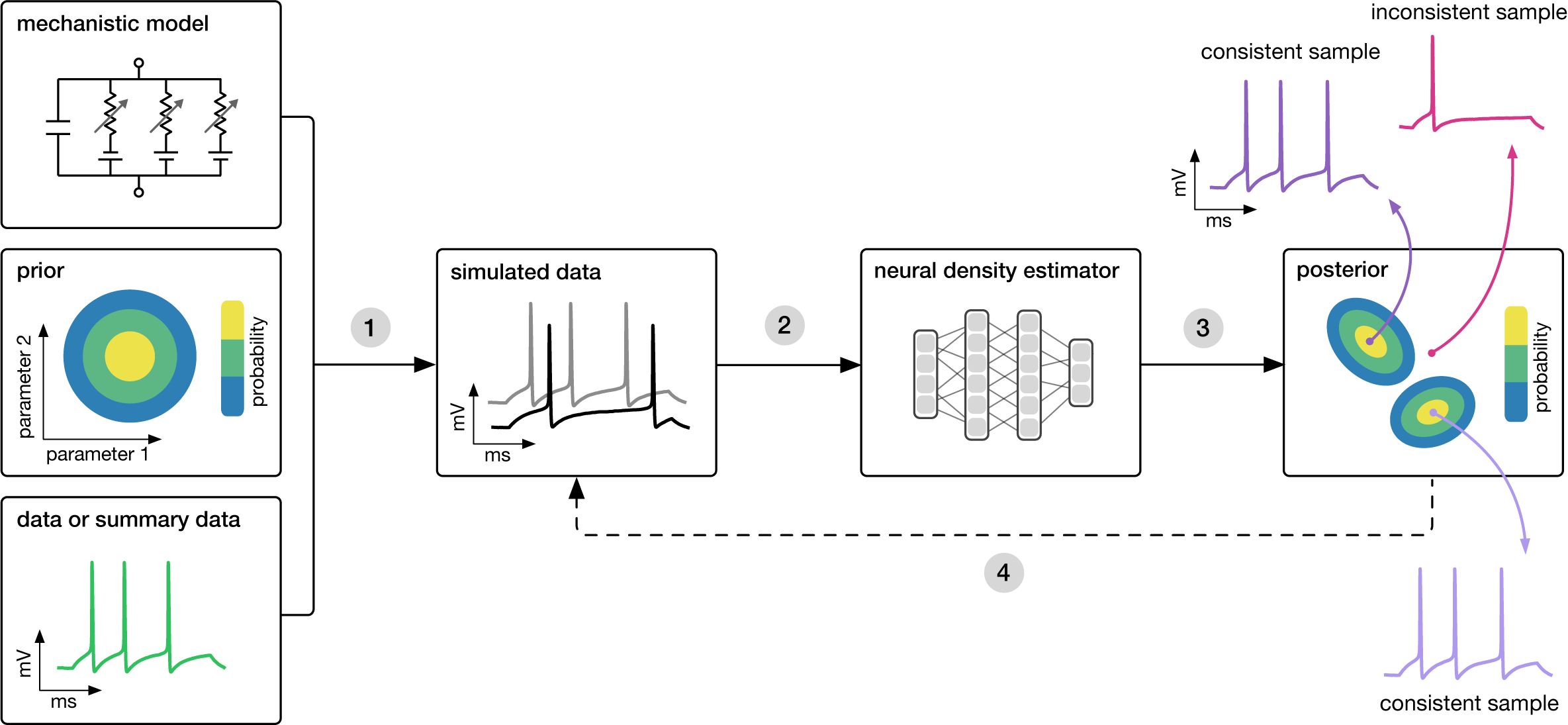
Inference method: SBI

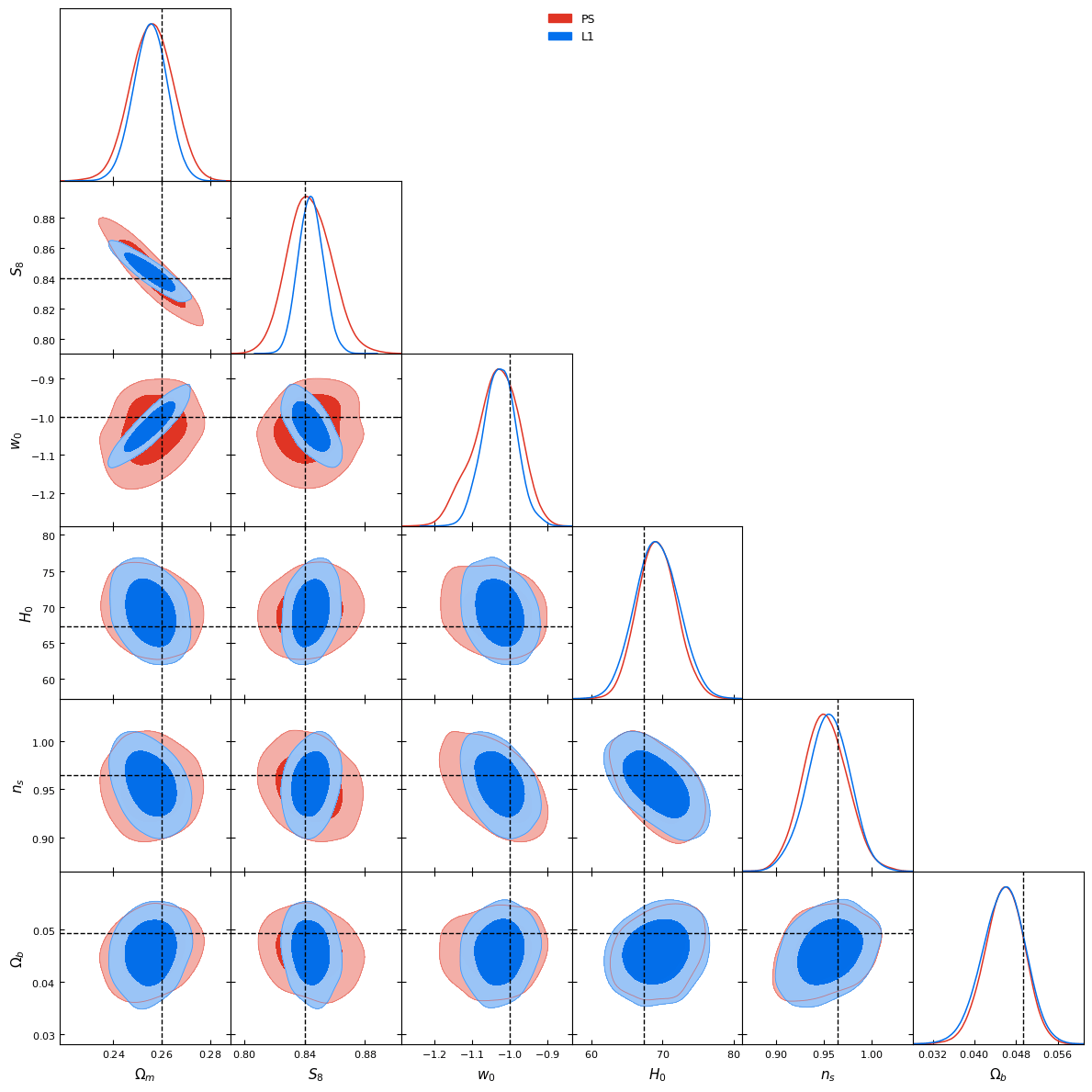
Power spectrum vs l1-norm (scale: ~10arcmin)

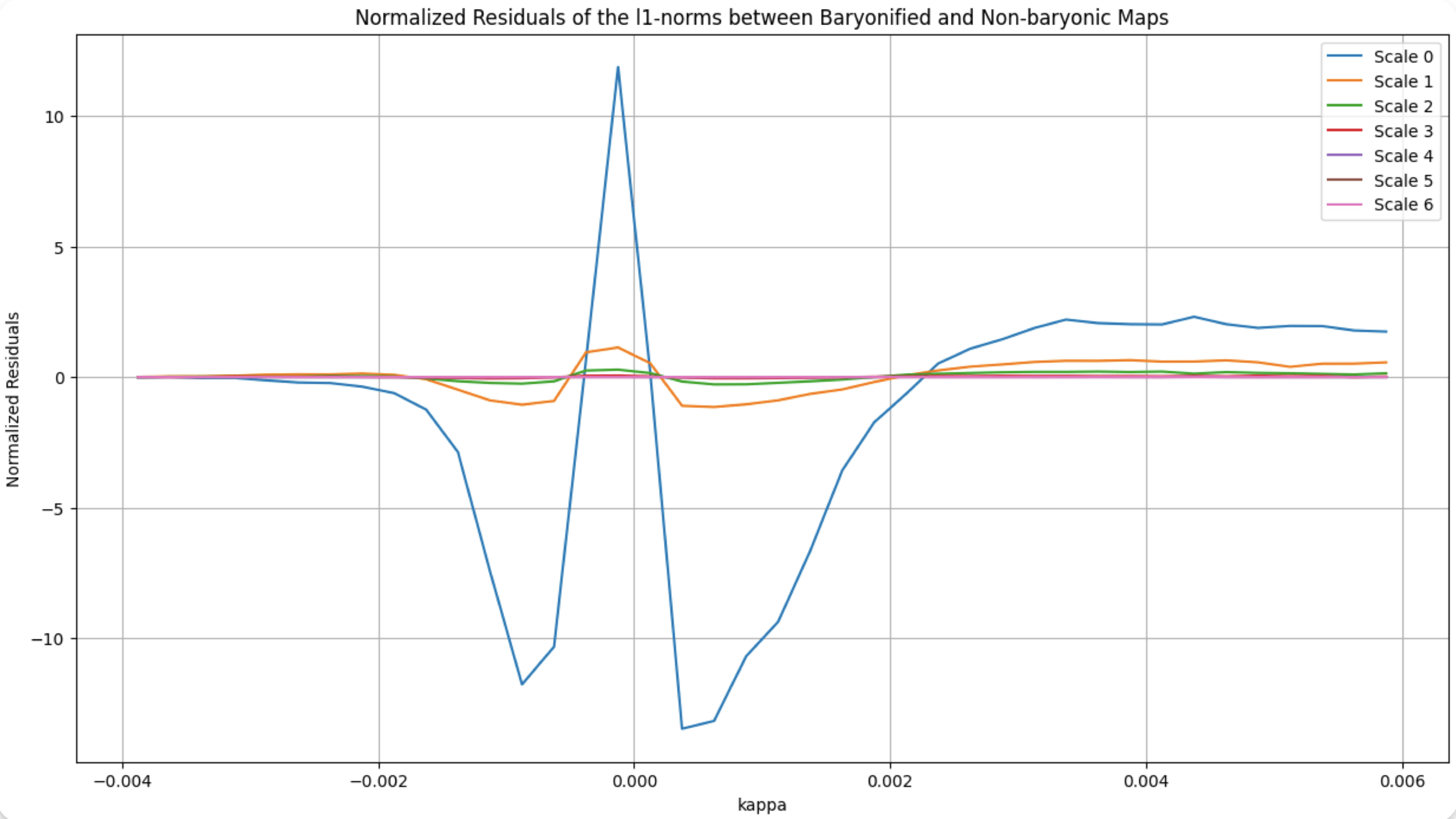
What about the baryonic effects? Do we have any bias?

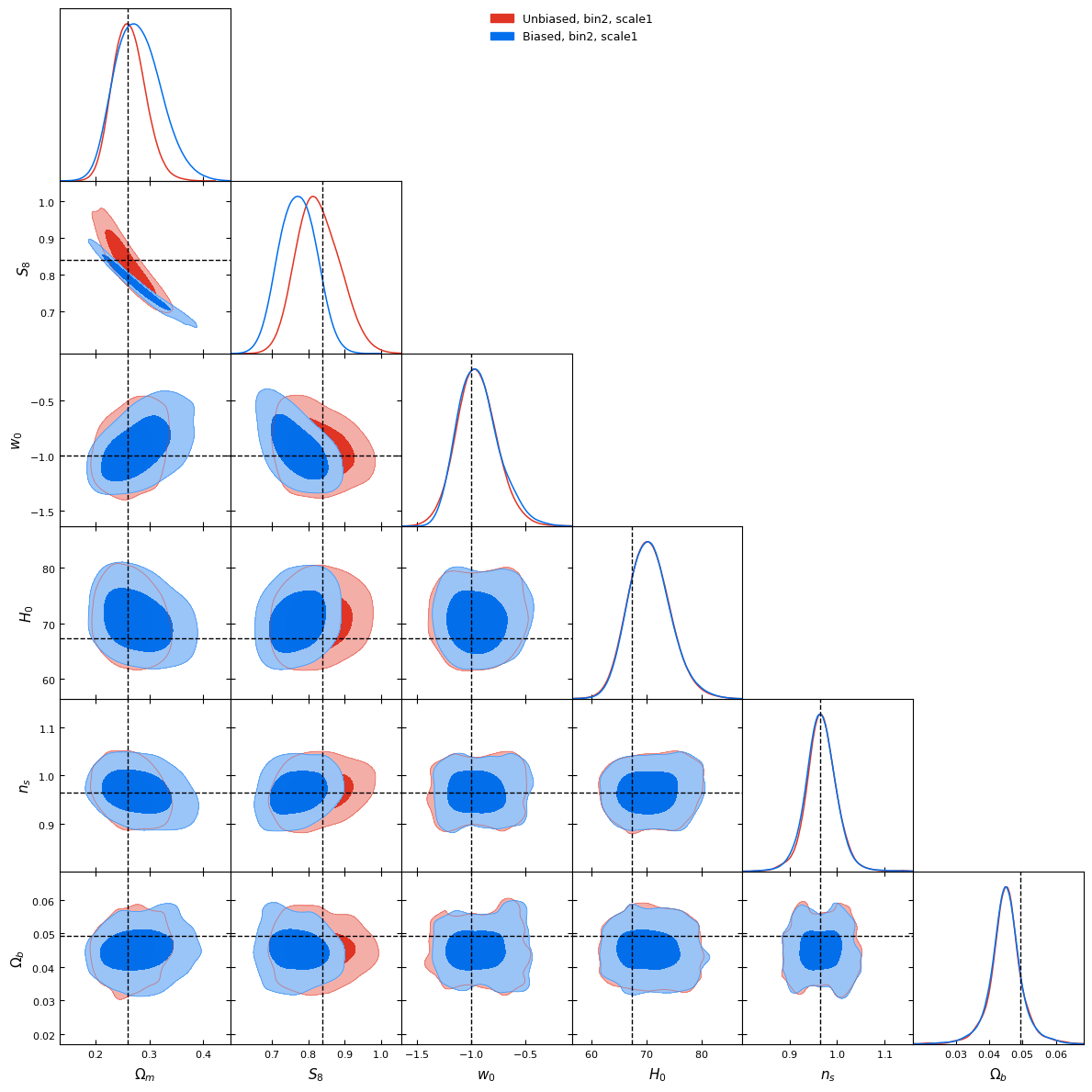
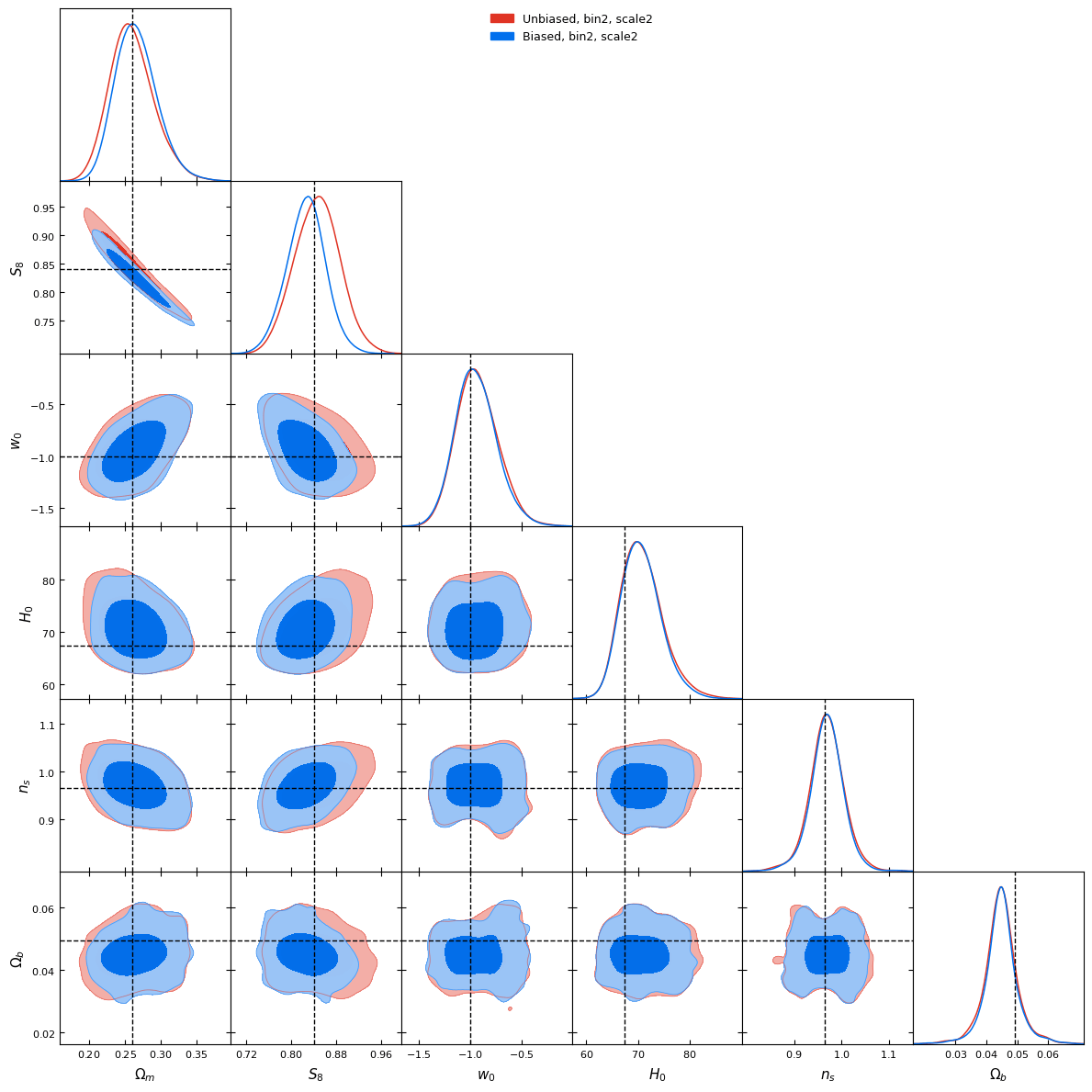
l1-norm, scale 1 (~10arcmin)

l1-norm, scale 2 (~20arcmin)

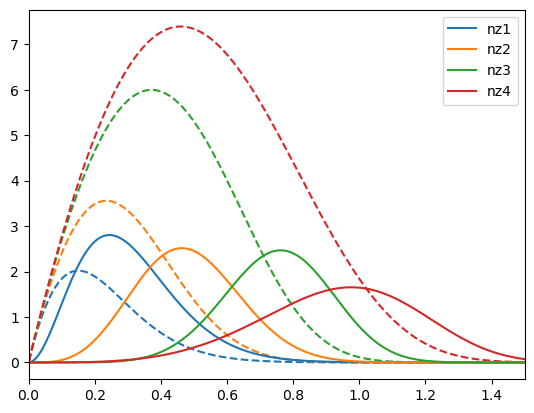
Weak lensing tomography

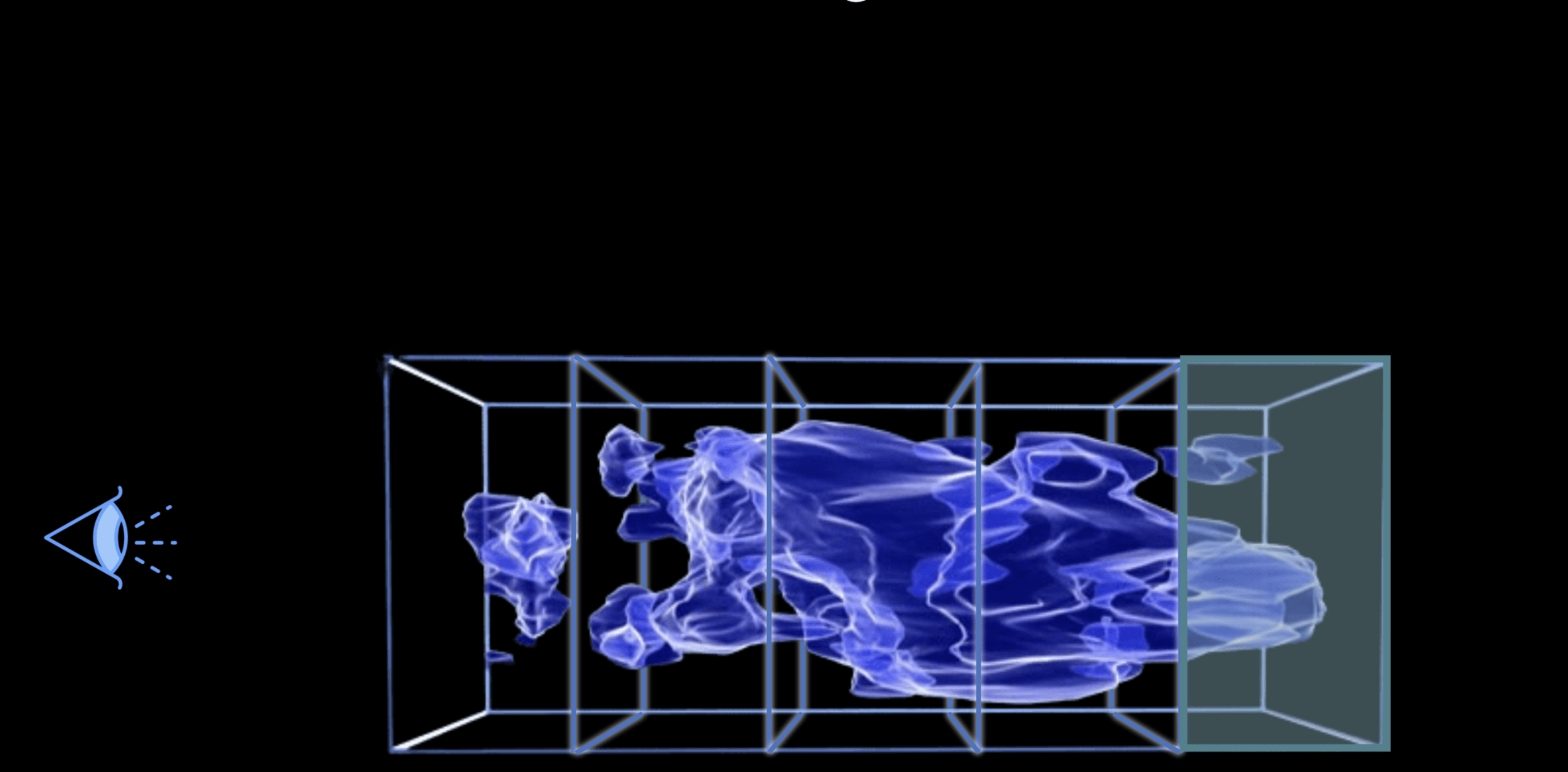
Weak lensing tomography

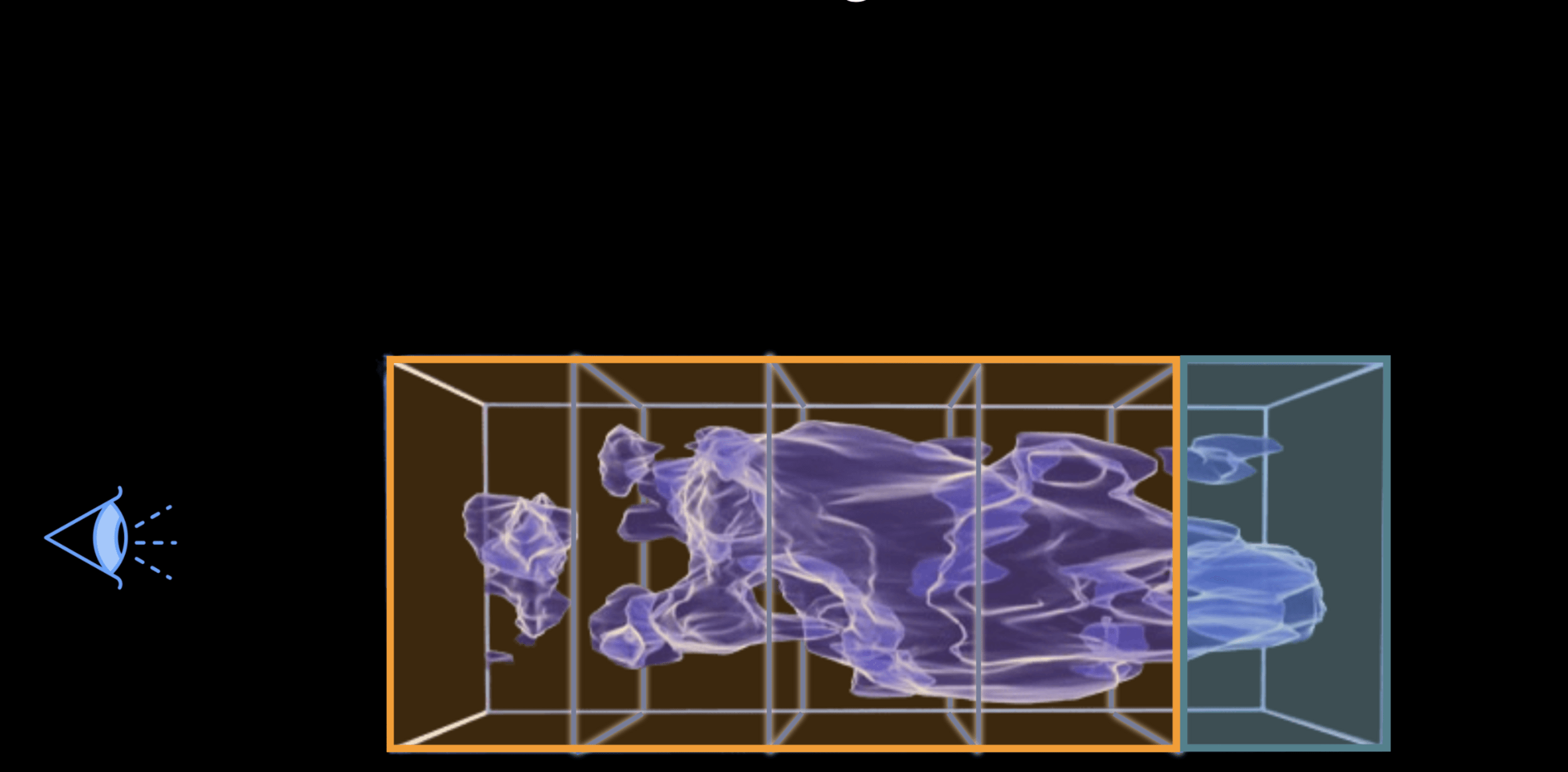
Weak lensing tomography

Weak lensing tomography

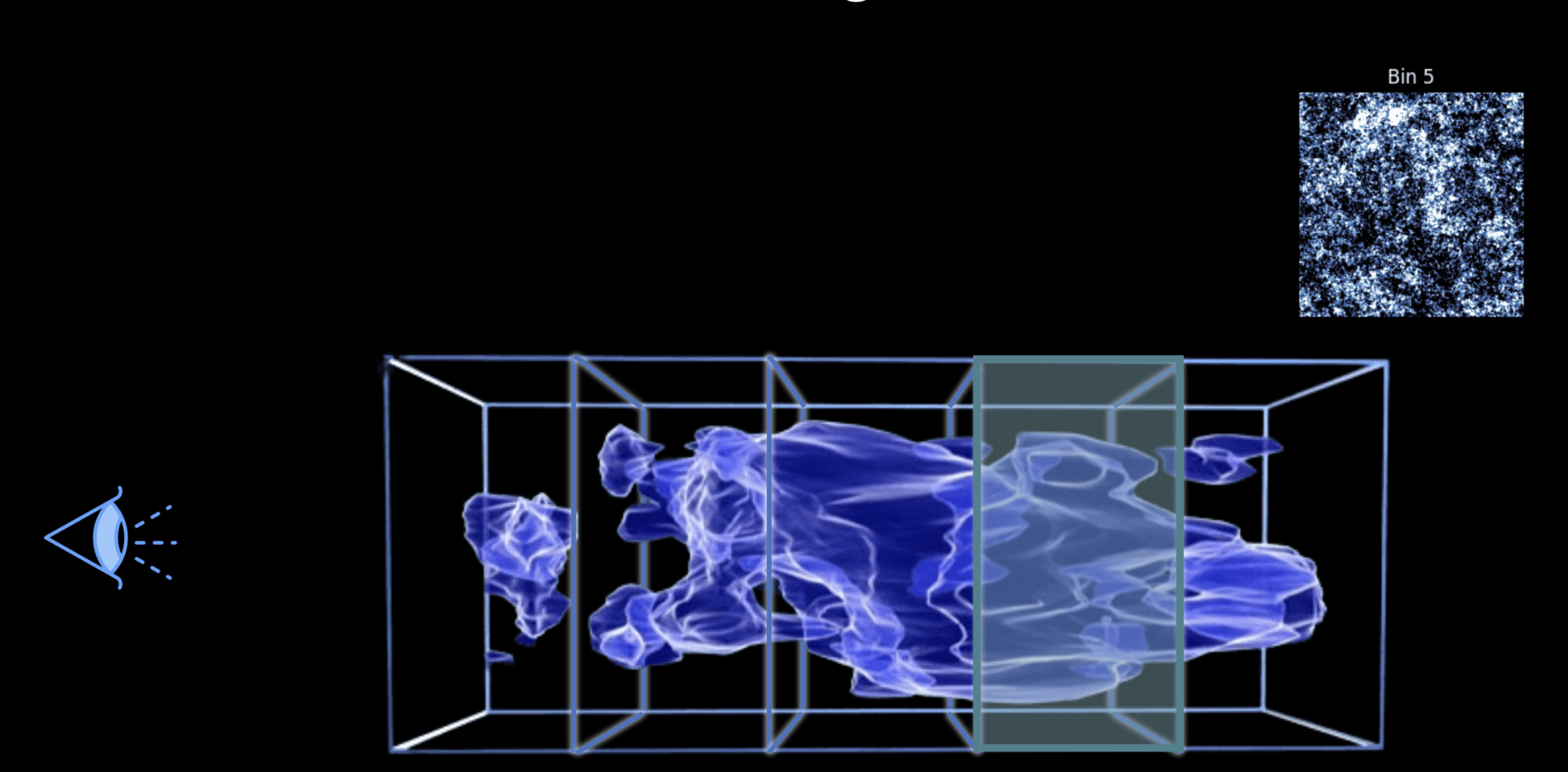
Weak lensing tomography

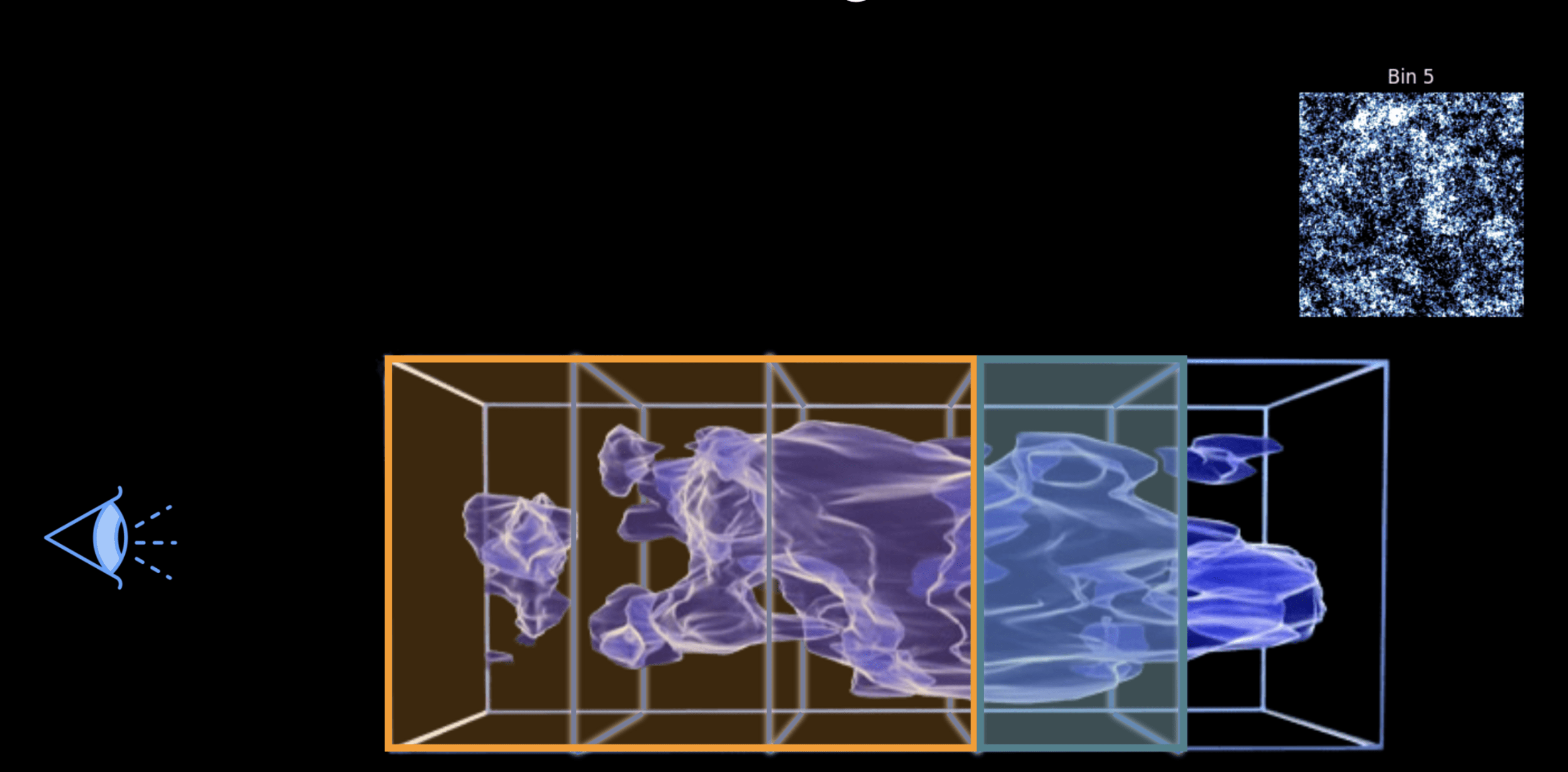
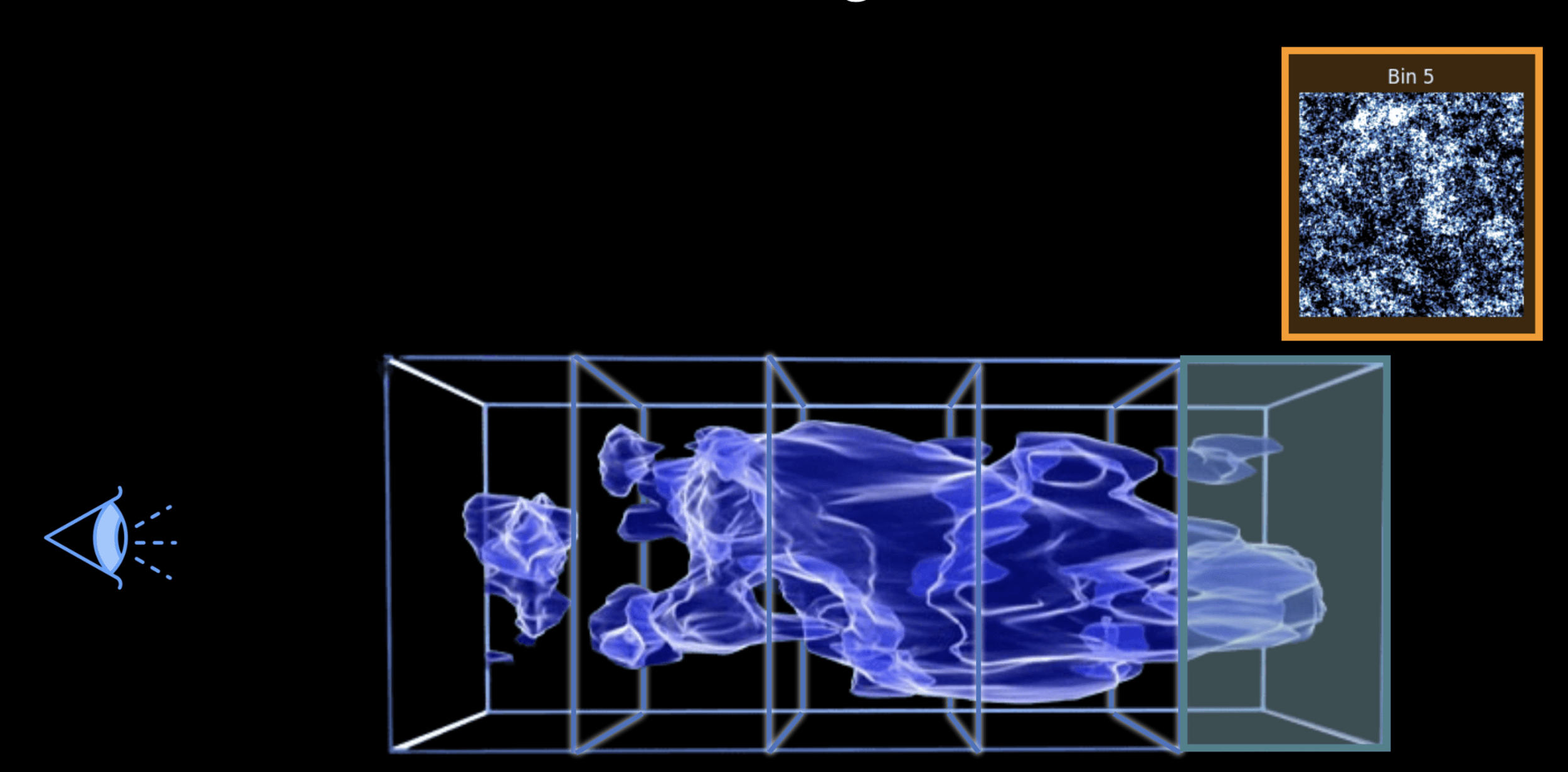
Weak lensing tomography

Weak lensing tomography

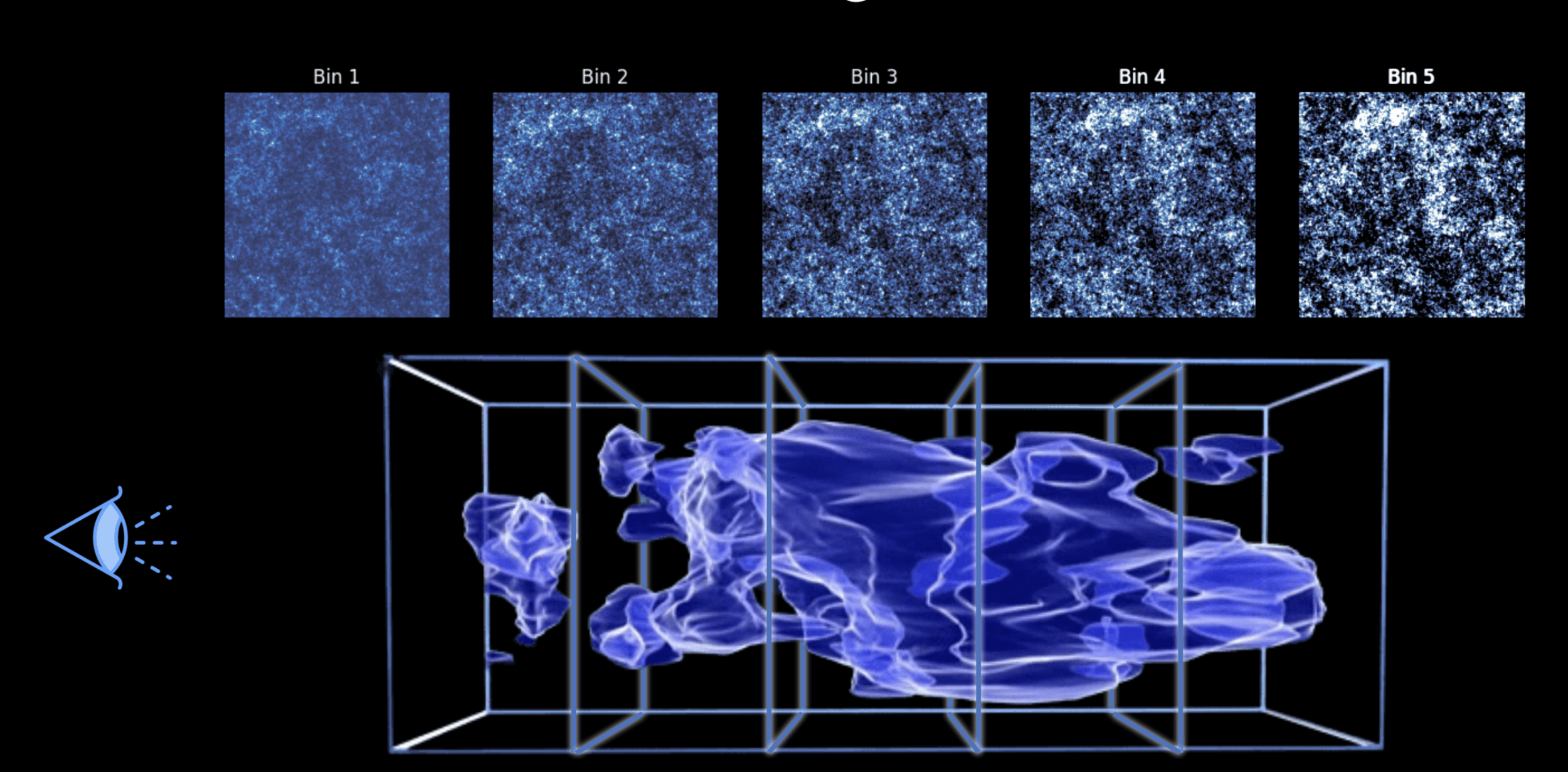
Weak lensing tomography

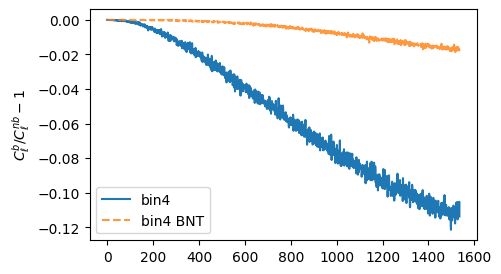
BNT transform

When we observe cosmic shear, contributions come from mass at different redshifts.
This creates projection effects: large and small-scale structures get mixed up.
These effects make it harder to accurately analyze data and extract information

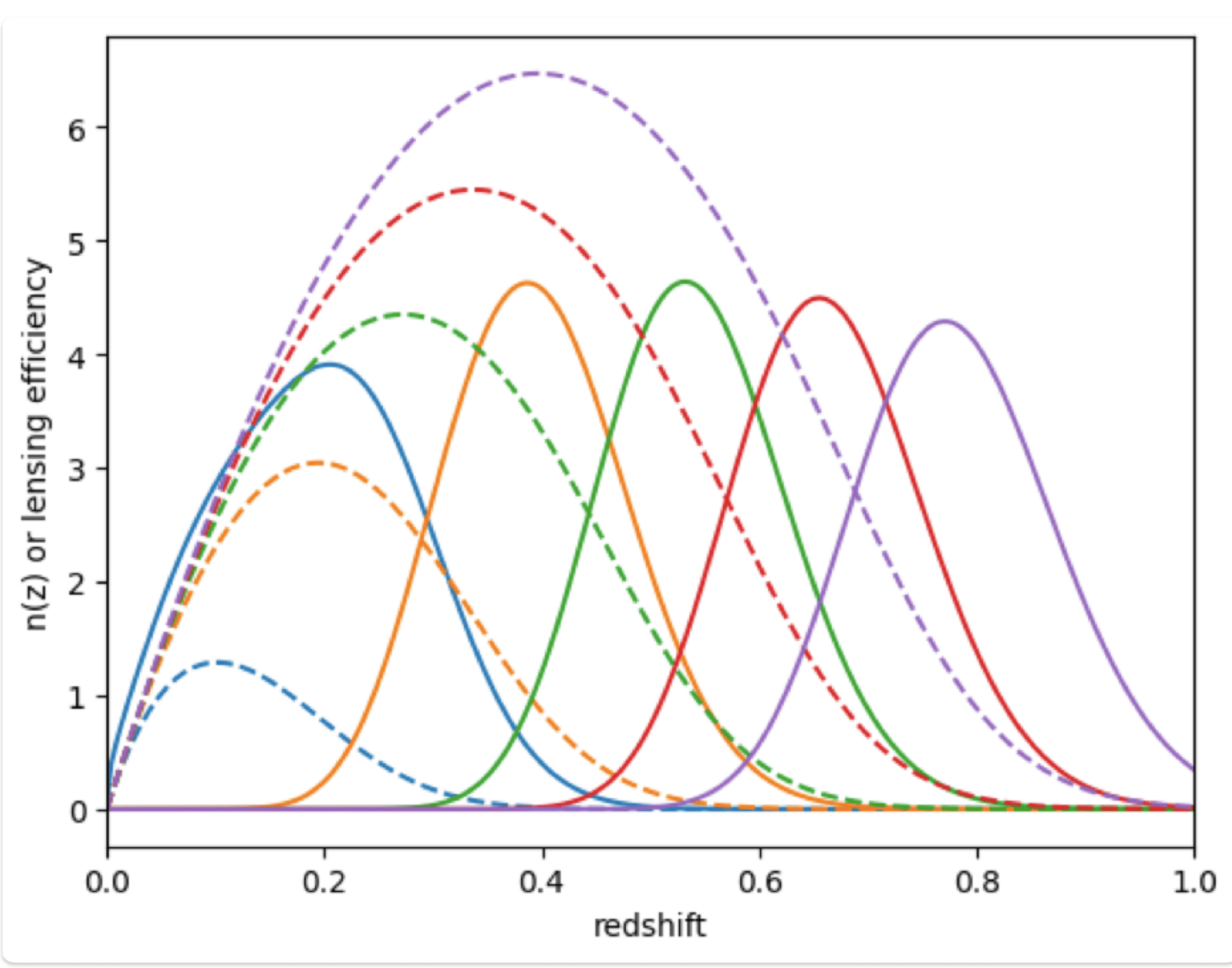
BNT transform

BNT Transform: A method to “null” or remove contributions from unwanted redshift ranges.
It reorganizes the weak-lensing data so that only specific redshift ranges contribute to the signal, making it easier to analyze.
It focuses on isolating lensing contributions by sorting out overlapping signals.

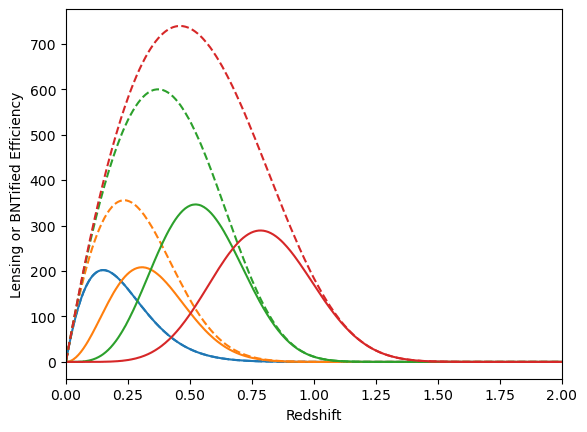
How are statistics impacted?

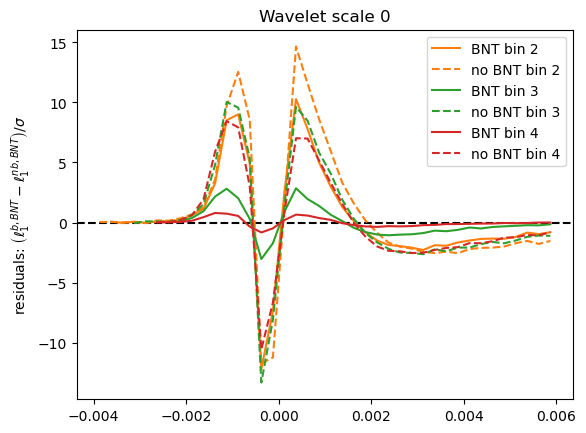
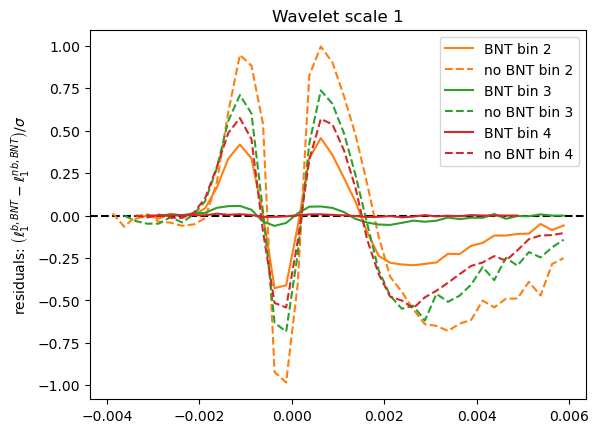
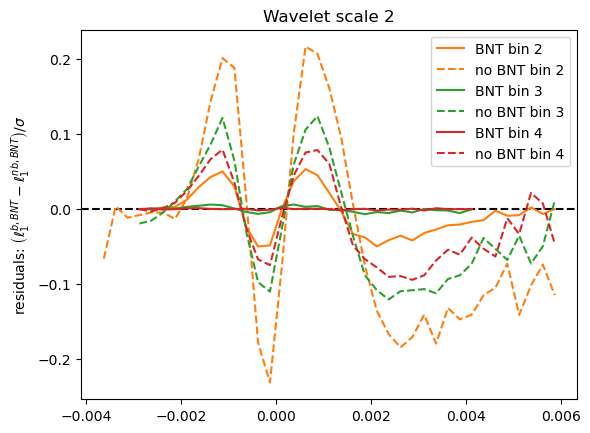
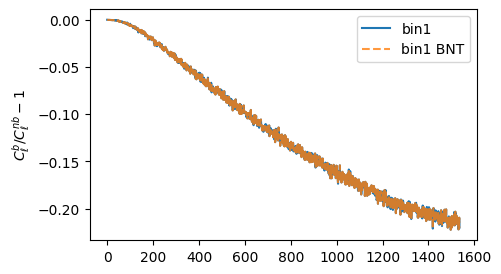
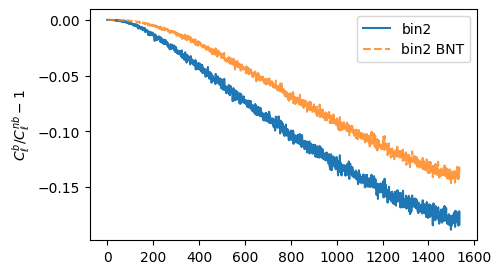
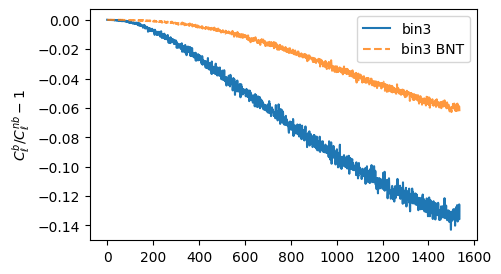
What about contours?

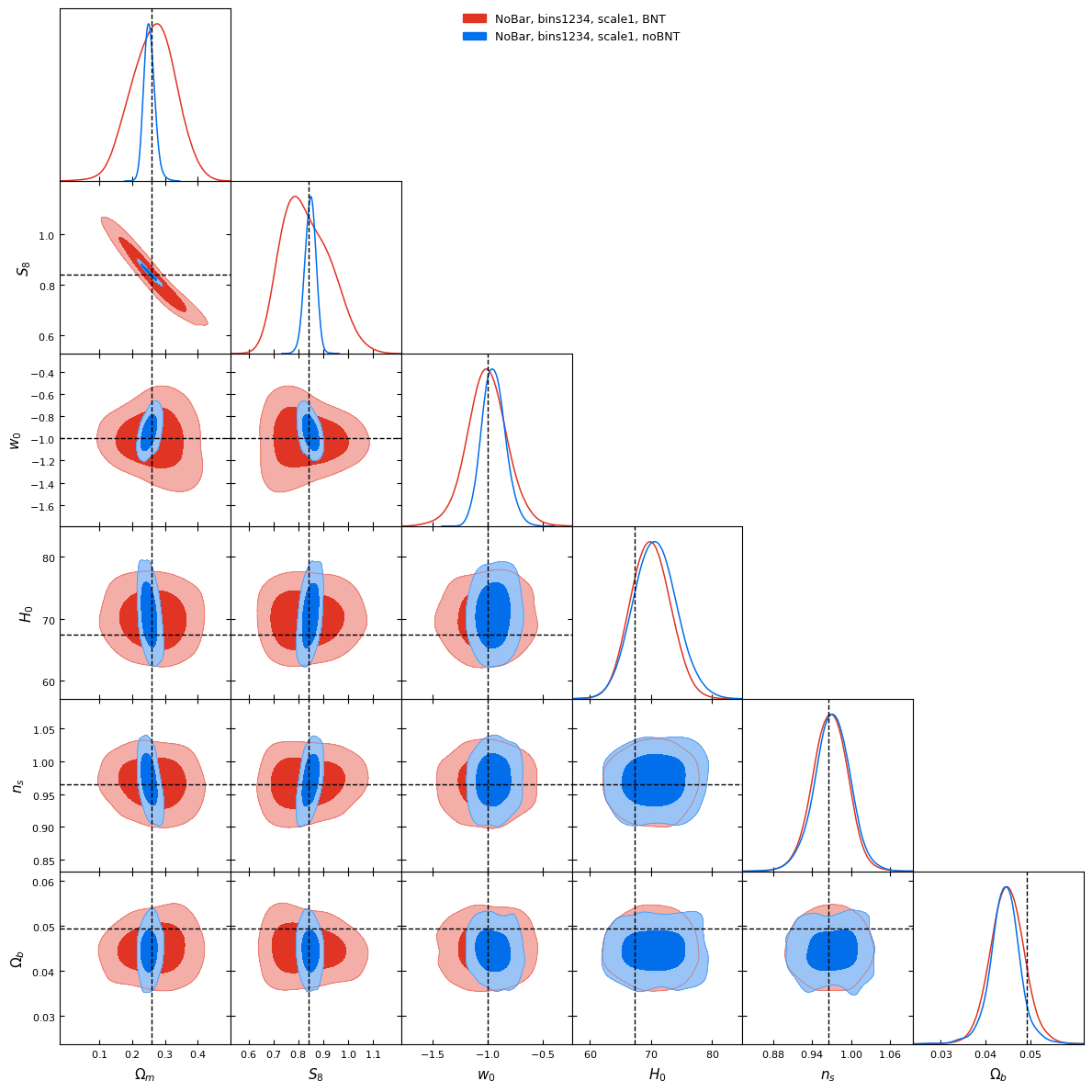
Scale 1 (~7arcmin)

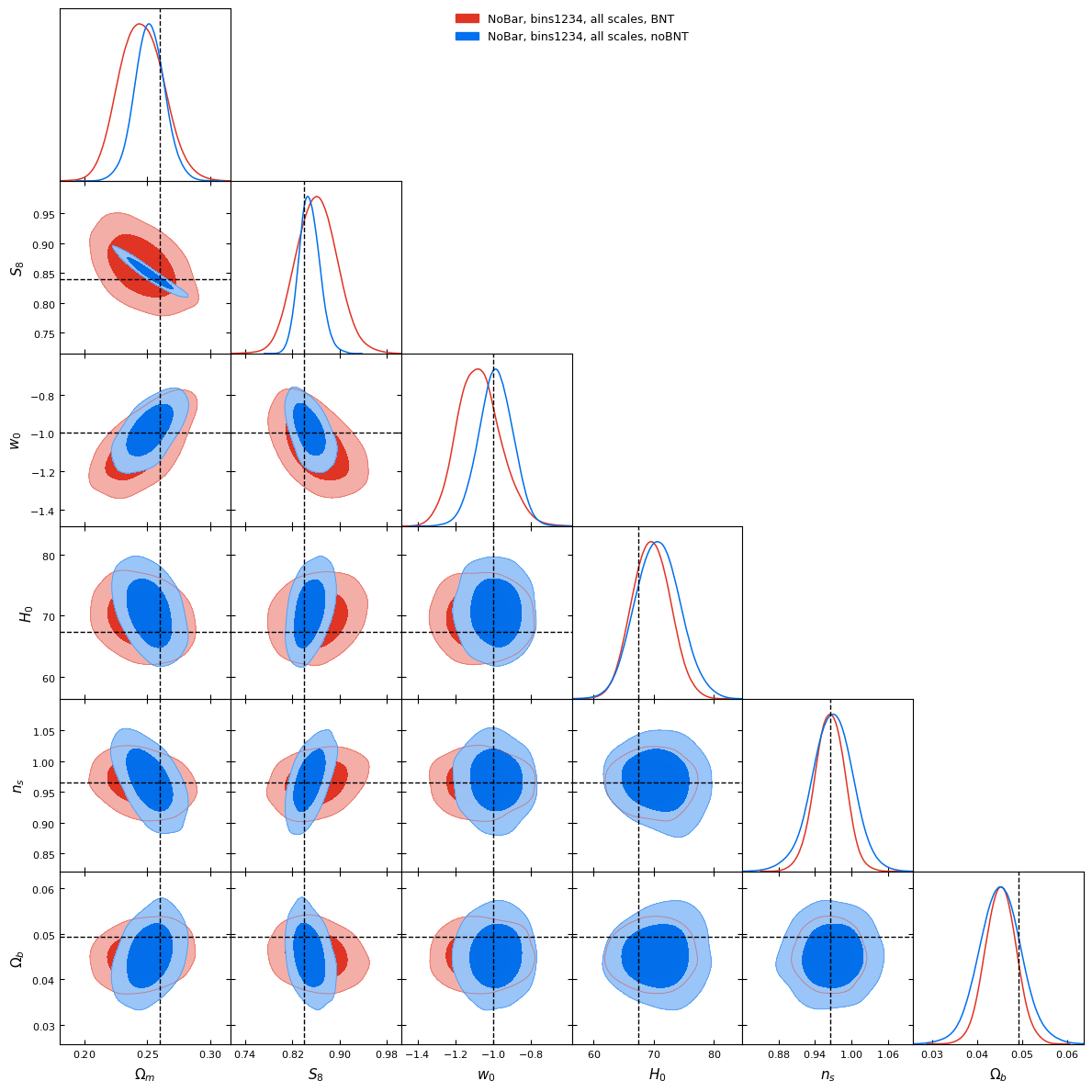
Multiscale

Why this reduction in constraining power?

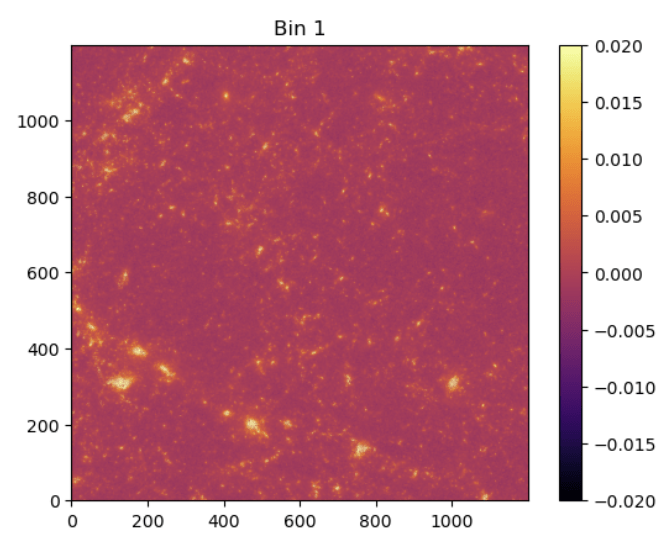
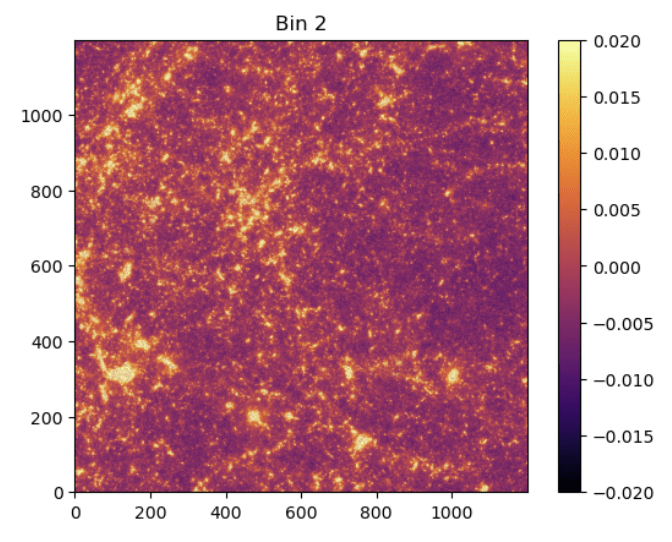
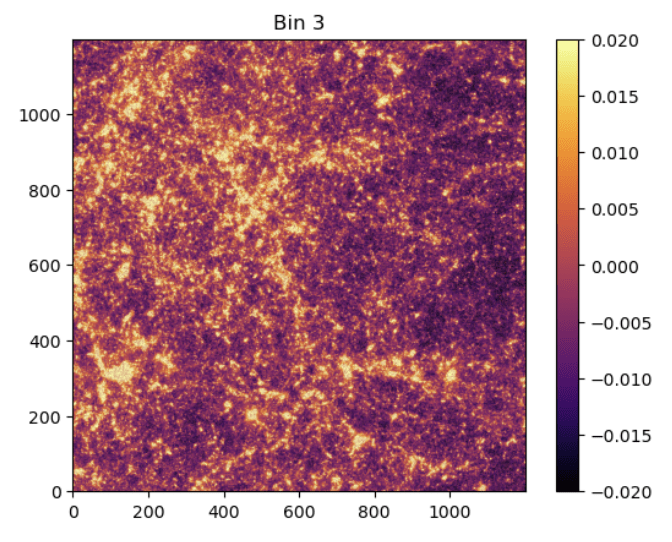
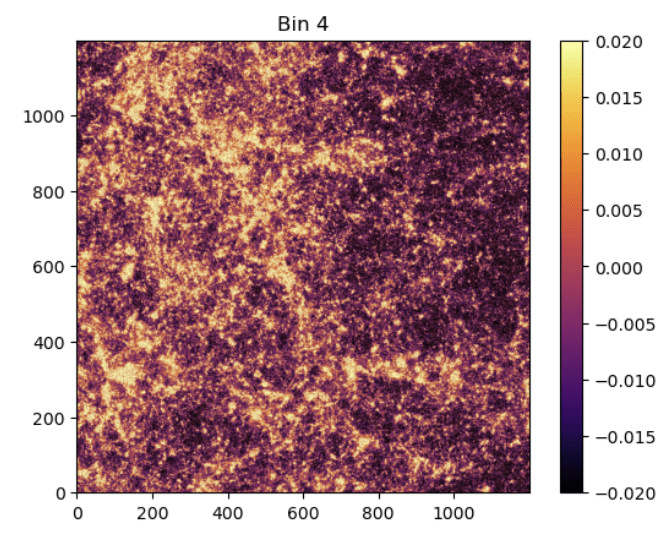
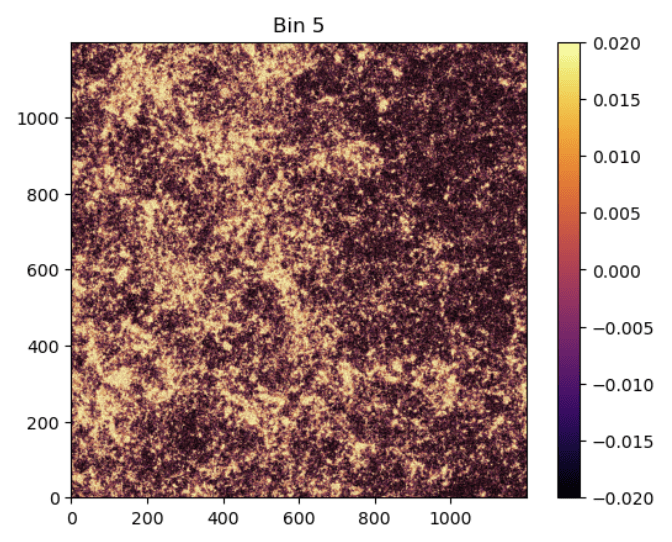
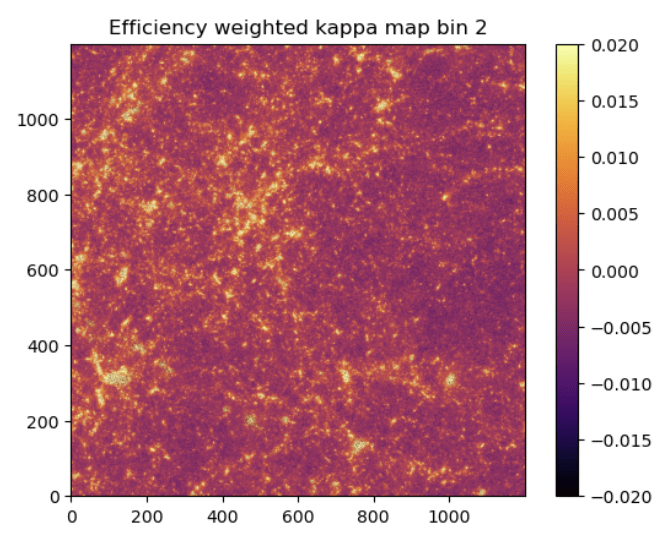
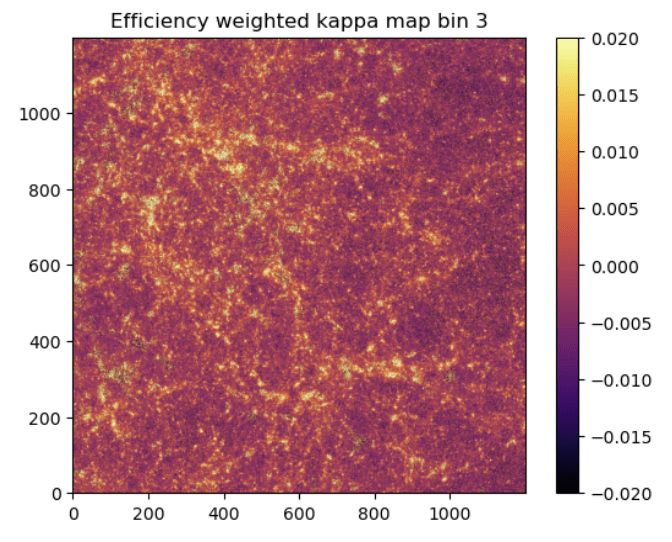
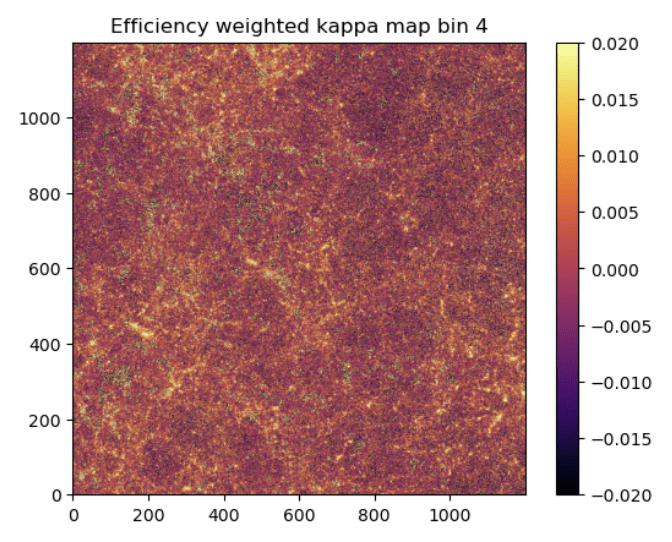
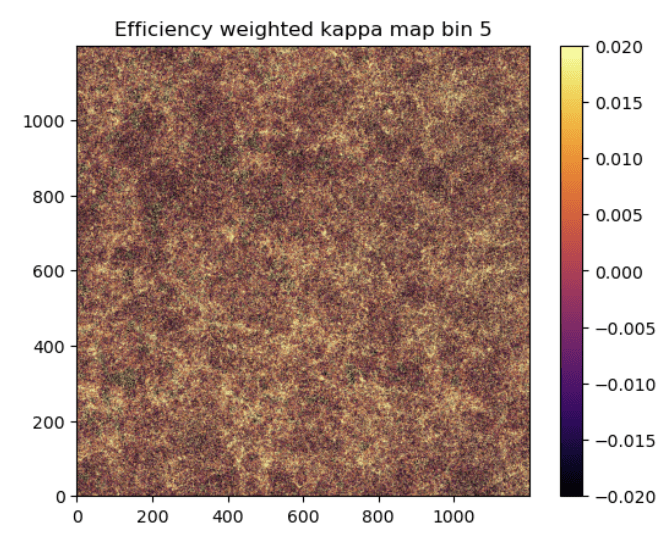
no BNT

BNT

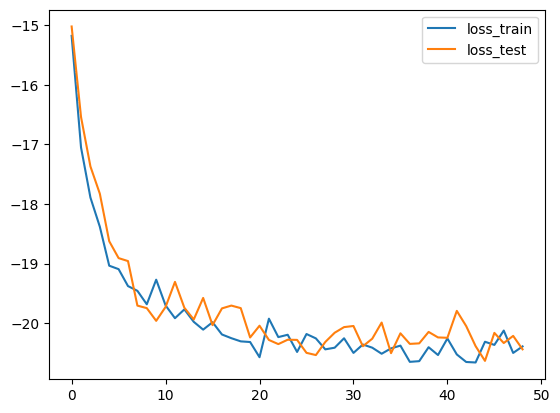
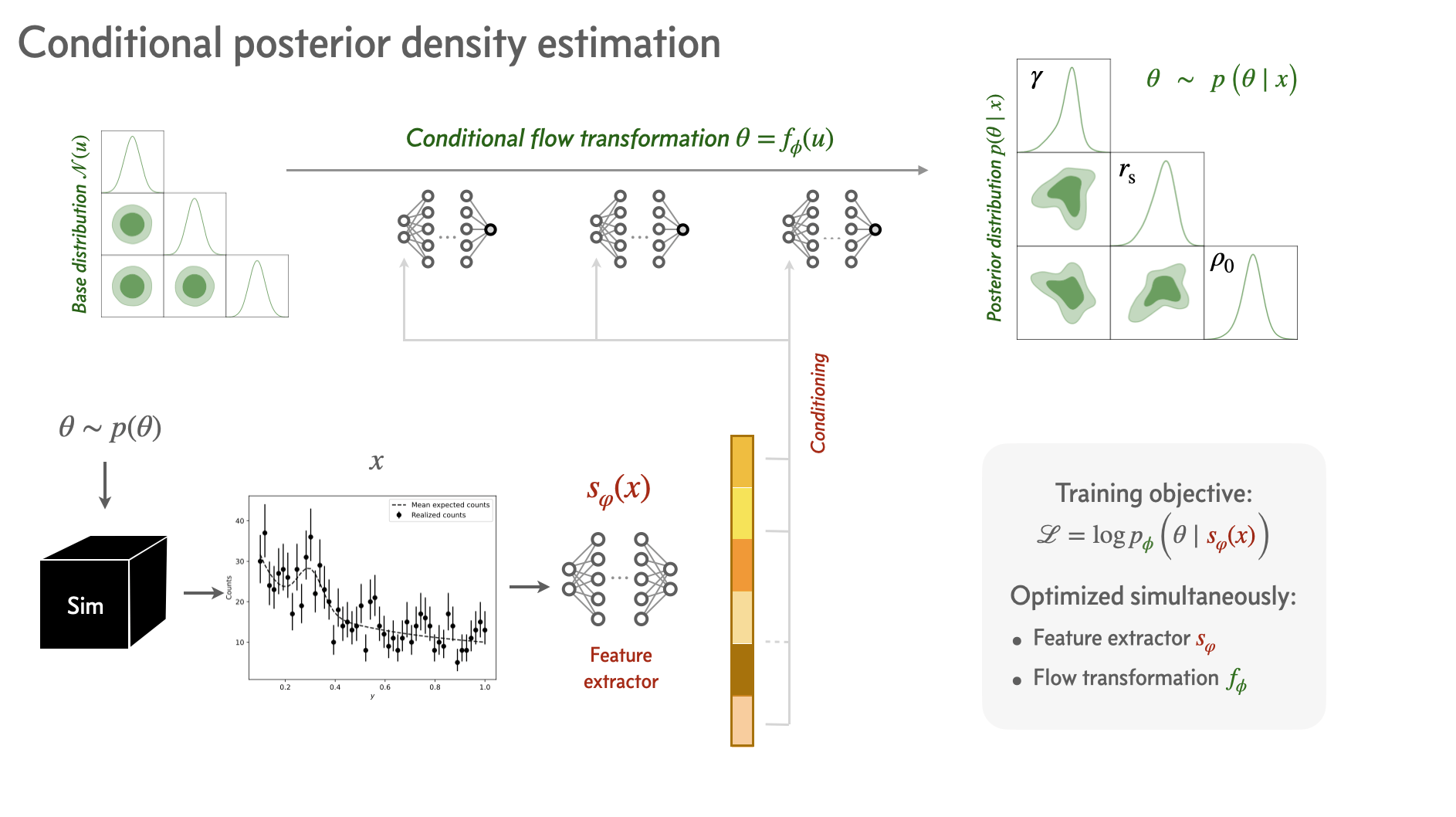
Hope: Neural Summaries (VMIM)