Building the Euclid Digital Twin: FLI with Hybrid Physical-Neural Differentiable Models

Andreas Tersenov

16 January  2026

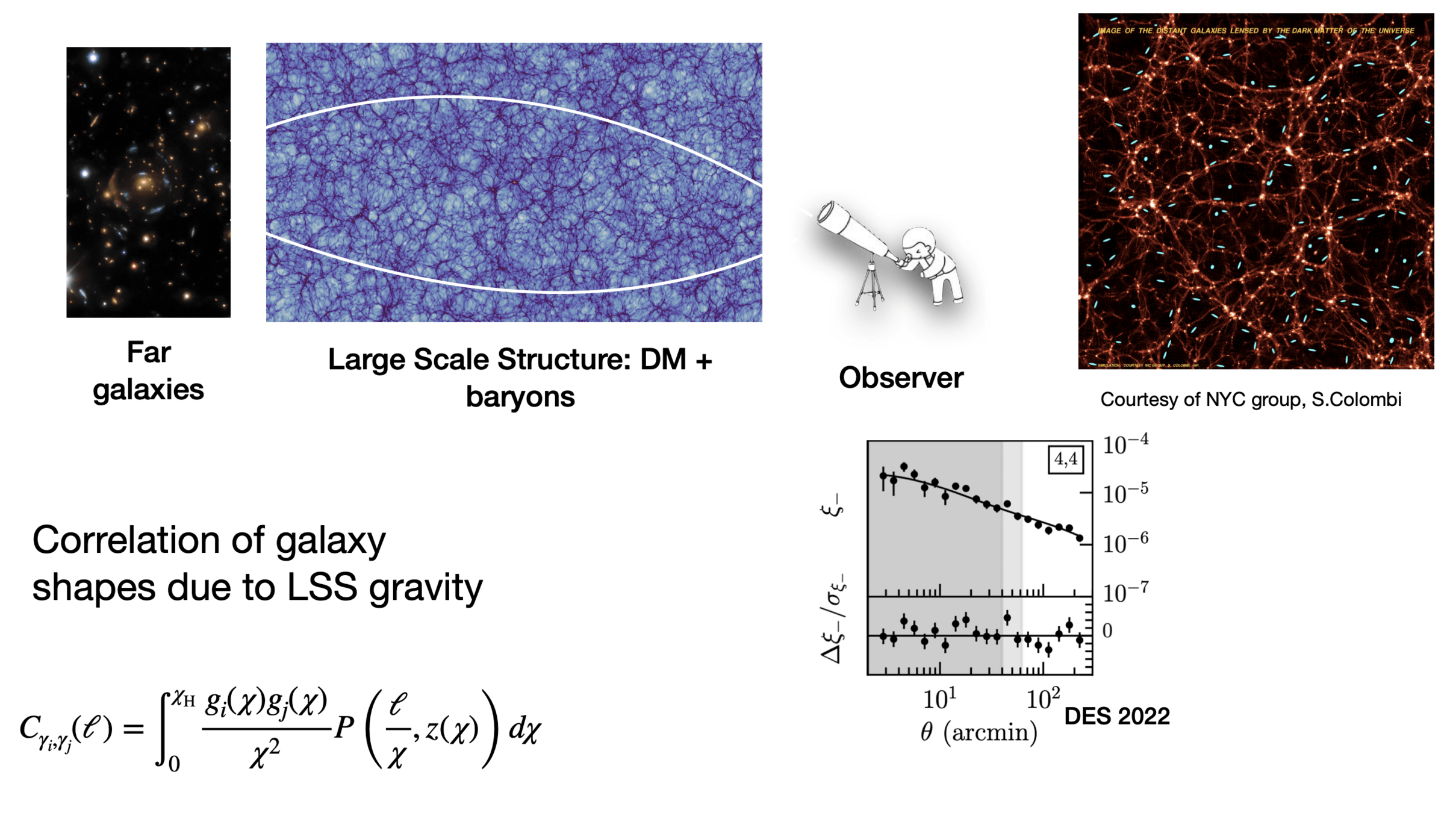
Background: Weak Lensing Analysis

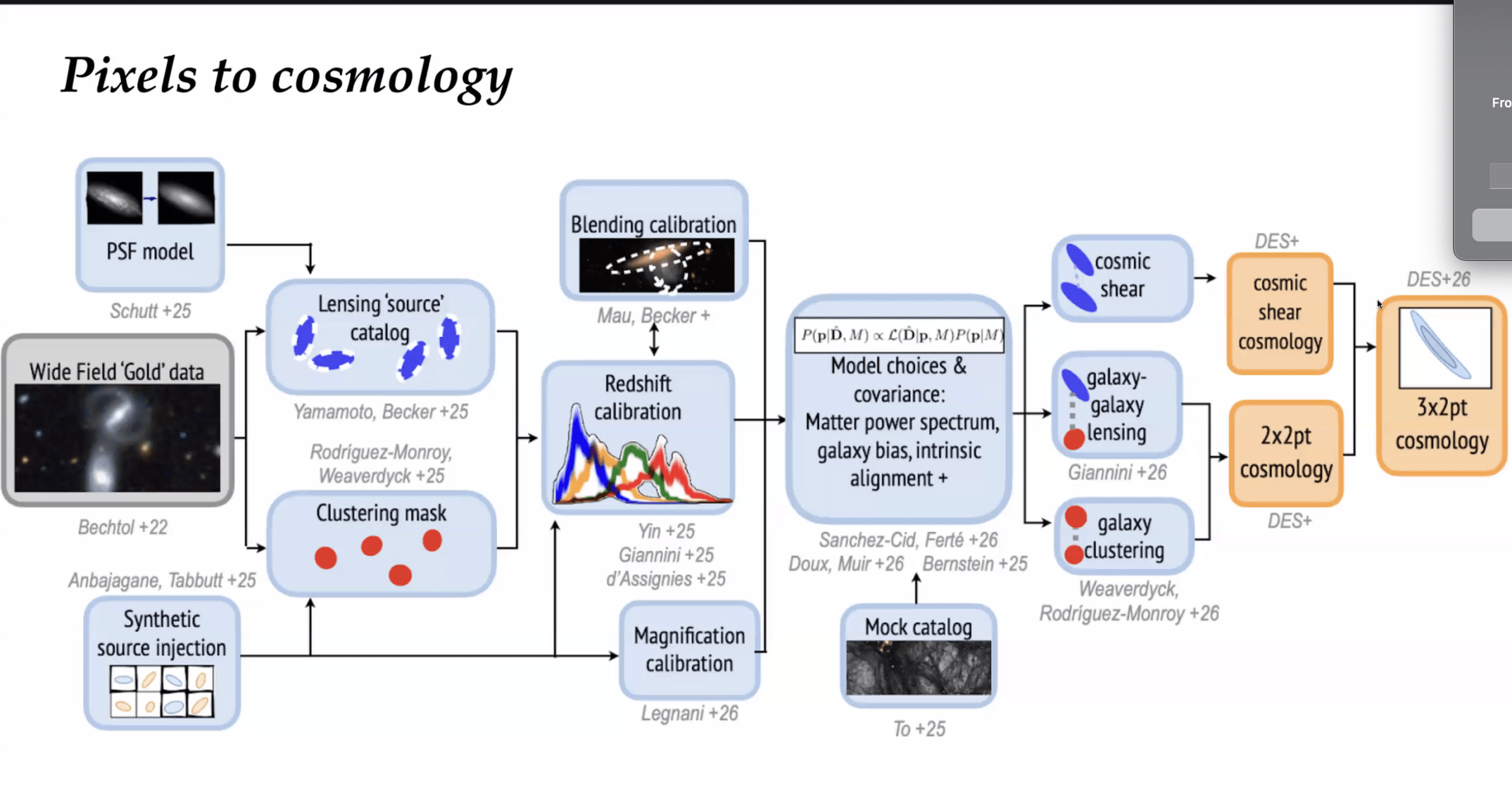
An End-to-End approach: From Pixel-Level Reconstruction to Robust Cosmology

The Data/Pixels

  • Catalogues: shear calibration, masks, blinding, tomography...

  • Mass Mapping: Inverse problems, PnPMass, Denoising.

  • Methods: DL Priors, Convex Optimization.

The Signal & Physics

  • Summary Statistics: 2pt, HOS (Peaks, PDF, l1-norm)

  • Systematics: Baryonic Feedback, IA, Masks, Noise.

  • Theory: Large Deviation Theory validation, Euclid paper on theory HOS.

The Inference

  • Methodology: Simulation-Based Inference (SBI) & Likelihood-based Inference.

  • Computational Core: JAX ecosystem, Differentiable Programming, Samplers, ML-emulators.

Differentiable pipelines (JAX/PyTorch), ML/DL, probabilistic programming (NumPyro), advanced sampling, neural density estimation, ML/DL for scientific inference, and the diagnosis of model misspecification

Impact of Mass Mapping on Cosmology Inference

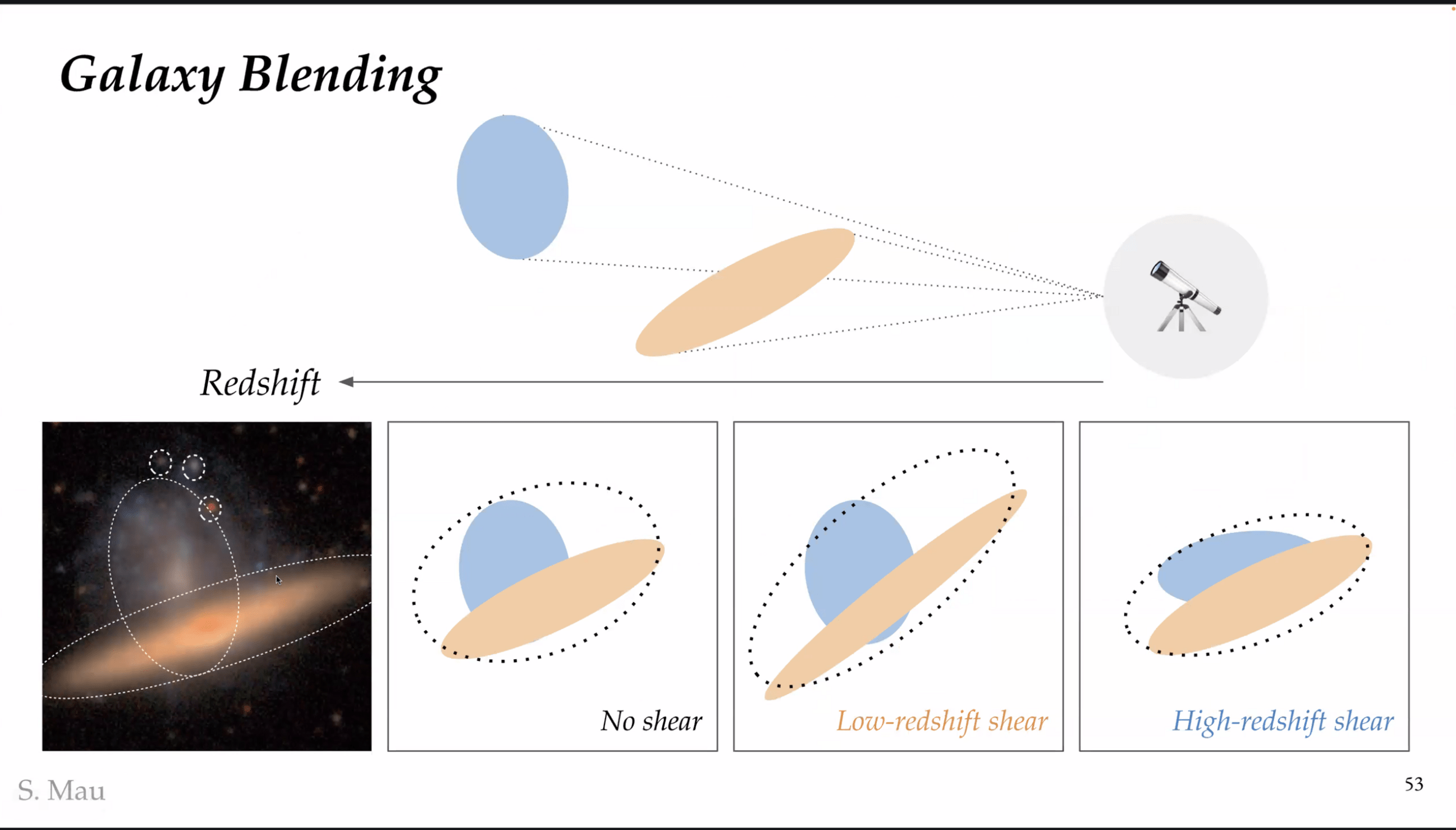
Weak Lensing Mass Mapping

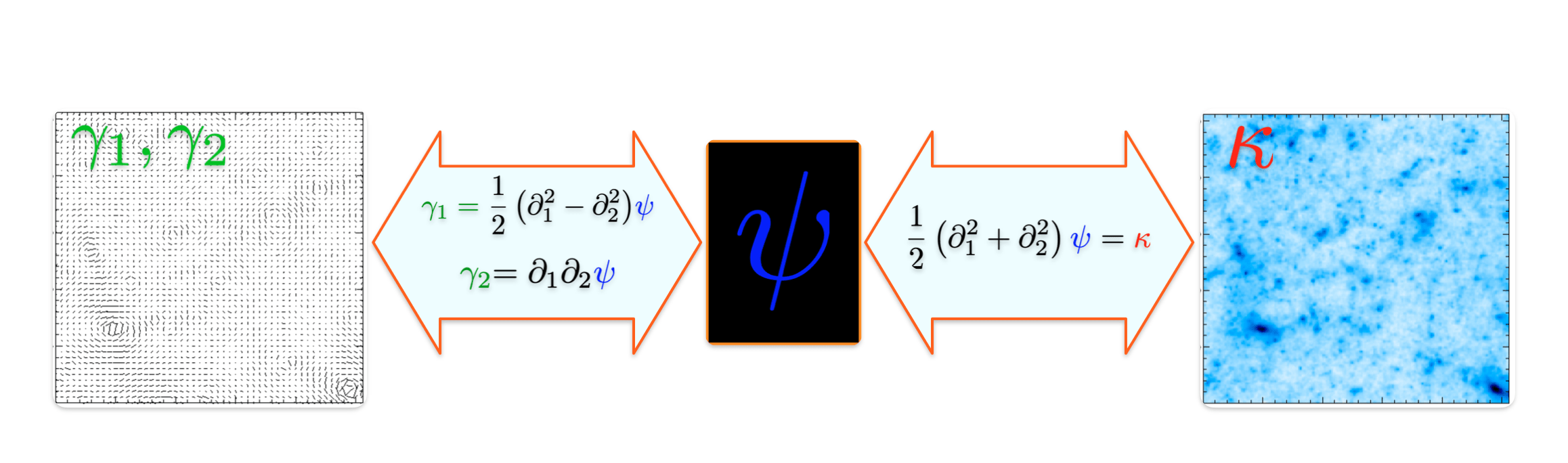
  • From convergence to shear: 
  • From shear to convergence: 
\gamma_i = \hat{P}_i \kappa
\kappa = \hat{P}_1 \gamma_1 + \hat{P}_2 \gamma_2

Mass mapping is an ill-posed inverse problem

Different algorithms have been introduced, with different reconstruction fidelities

But... does the choice of the mass-mapping algorithm have an impact on the final inferred cosmological parameters?

Or as long as you apply the same method to both observations and simulations it won't matter?

For which we have/assume an analytical likelihood function

x
t = f(x)

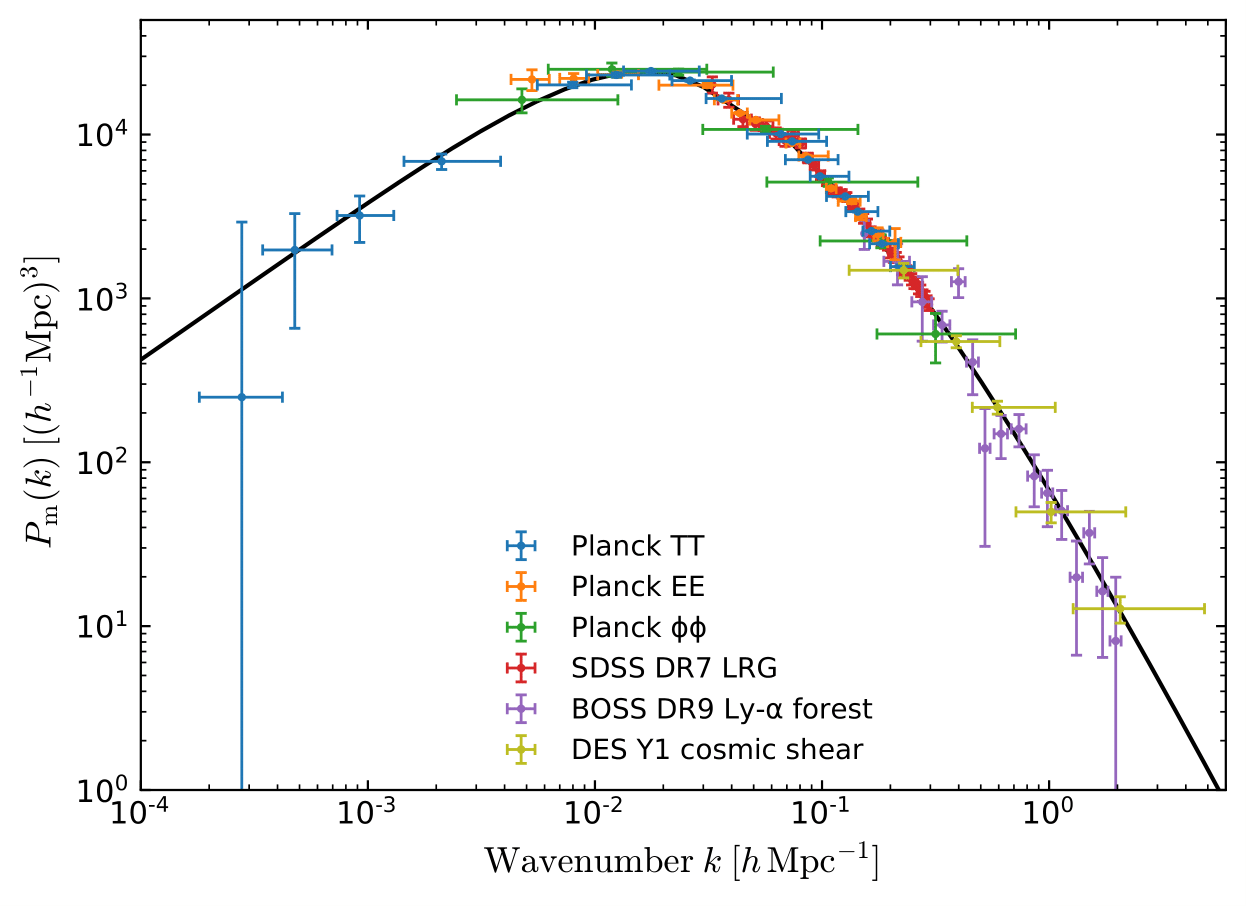
How to constrain cosmological parameters?

Likelihood → connects our compressed observations to the cosmological parameters

\underbrace{p\left(\theta \mid t=t_0\right)}_{\text {posterior }} \propto \underbrace{p\left(t=t_0 \mid \theta\right)}_{\text {likelihood }} \underbrace{p(\theta)}_{\text {prior }}
p\left(t=t_0 \mid \theta\right)

Credit: Justine Zeghal

2pt vs higher-order statistics

The traditional way of constraining cosmological parameters misses the non-Gaussian information in the field.

x
t = f(x)

​DES Y3 Results

Credit: Justine Zeghal

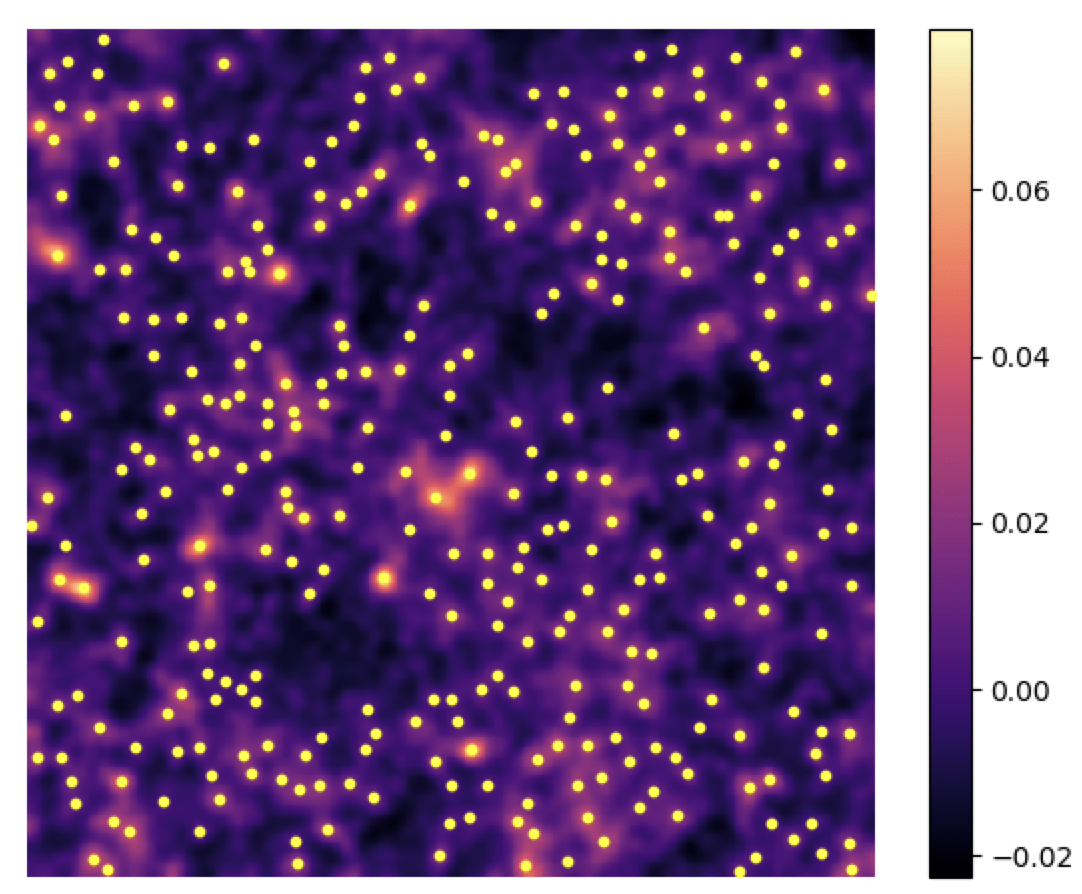
Higher Order Statistics: Peak Counts

=

+

+

+

+

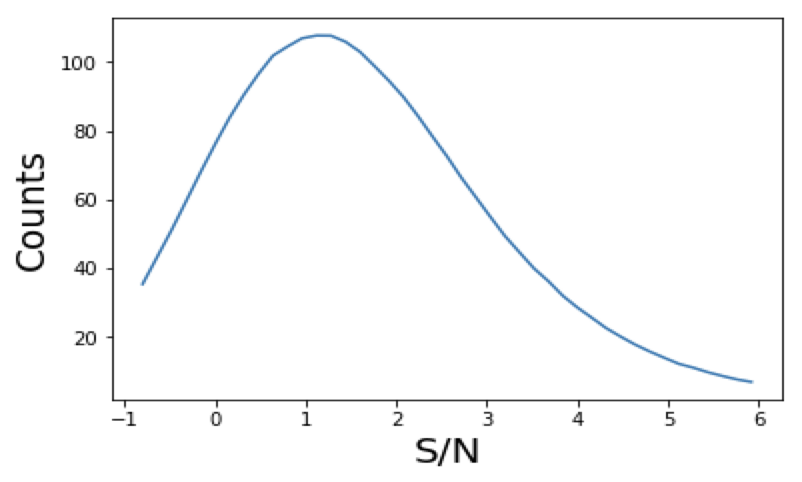
  • Peaks: local maxima of the SNR field
  • Peaks trace regions where the value of 𝜅 is high → they are associated to massive structures

Multi-scale (wavelet) peak counts

Ajani et. al 2021

cosmoSLICS pipeline

\begin{array}{ll} \hline \hline \text{Method} & \text{RMSE} \downarrow \\ \hline \text{KS } & 1.1 \times 10^{-2} \\ \text{iKS } & 1.1 \times 10^{-2} \\ \text{MCALens} & 9.8 \times 10^{-3} \\ \hline \end{array}
  • Add realistic masks & Euclid-like noise to shear maps
  • Use different algorithms for the mass mapping
  • Compression with higher-order statistics (peaks)
  • Gaussian Likelihood + MCMC

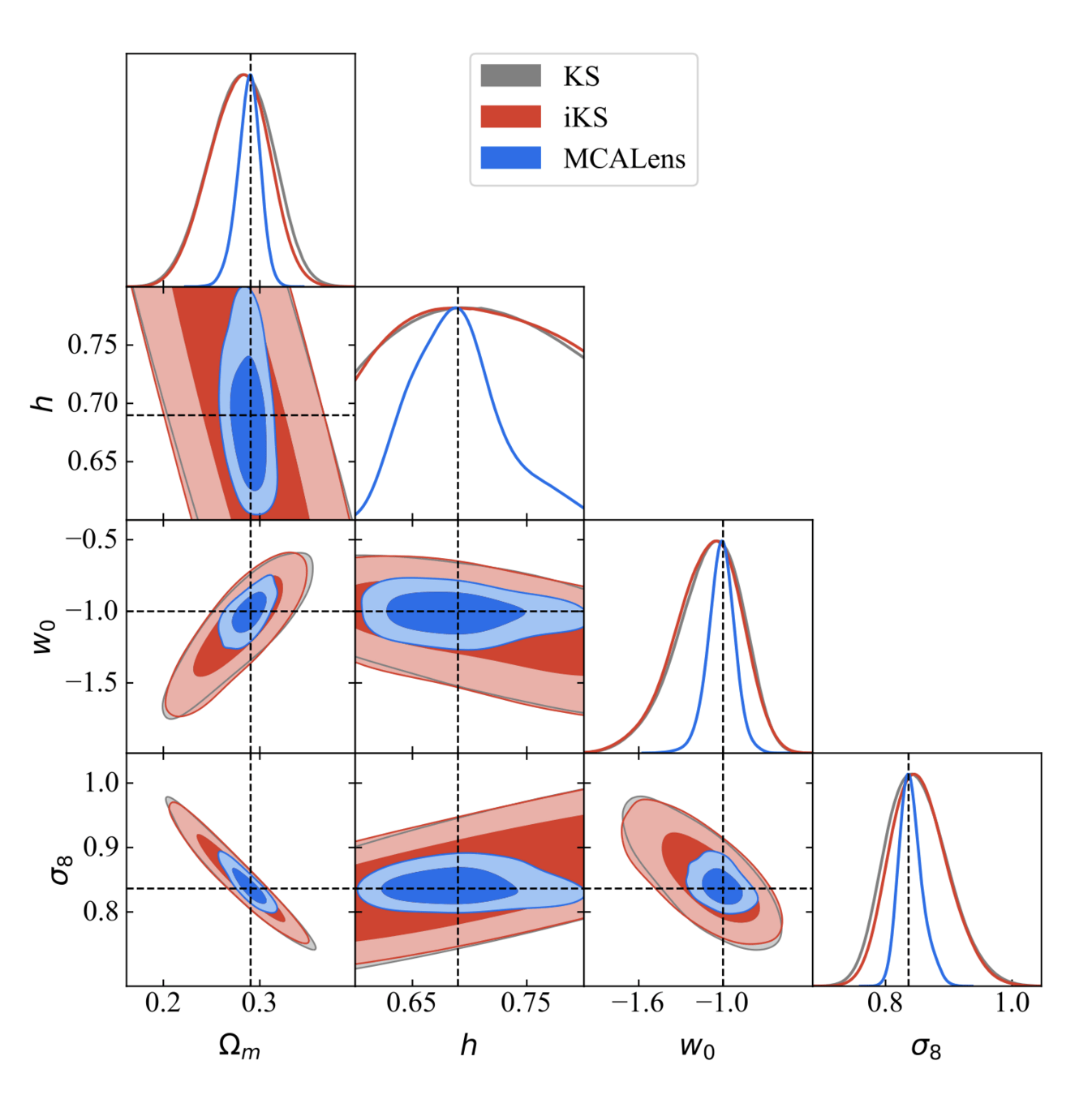
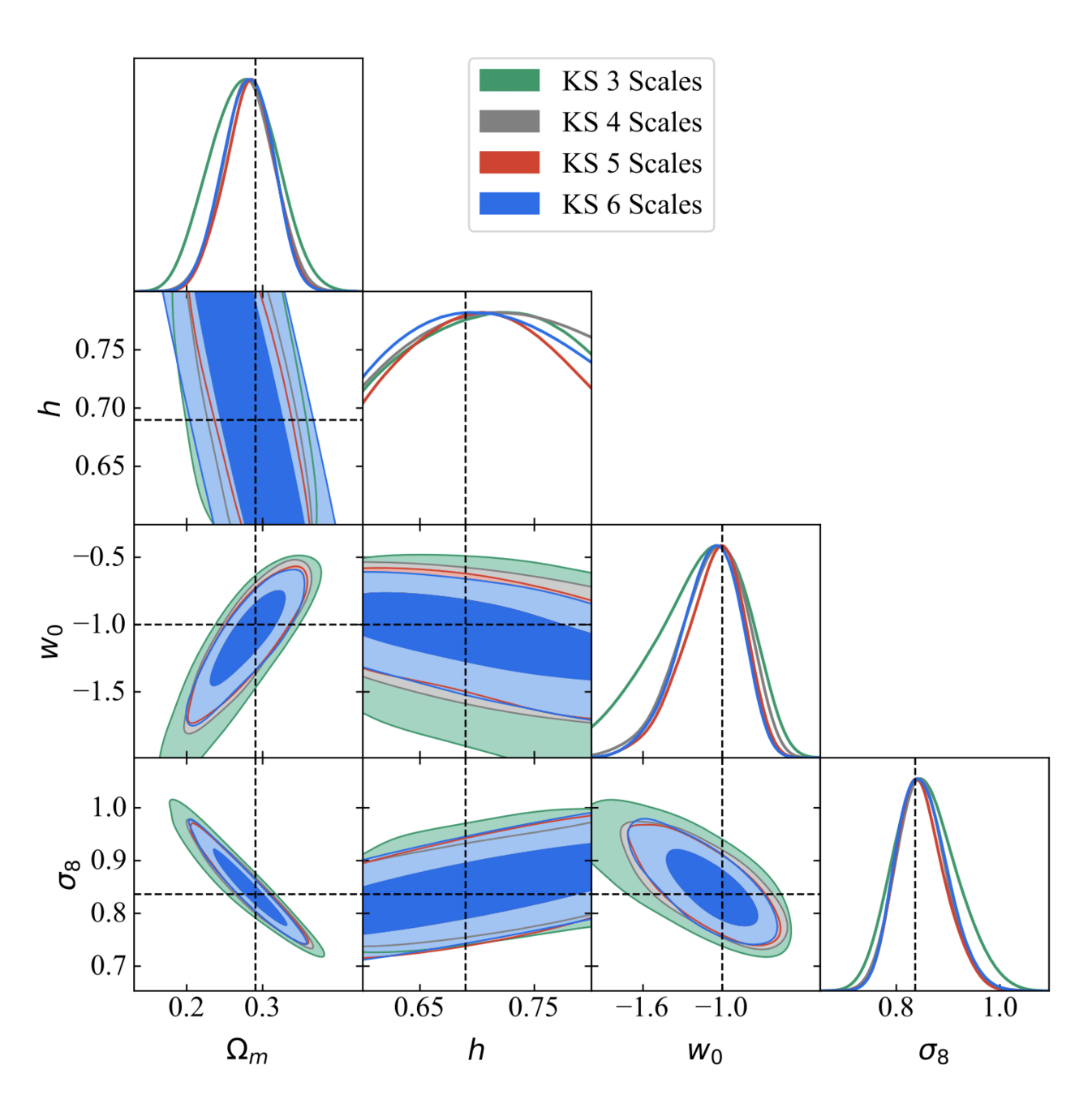
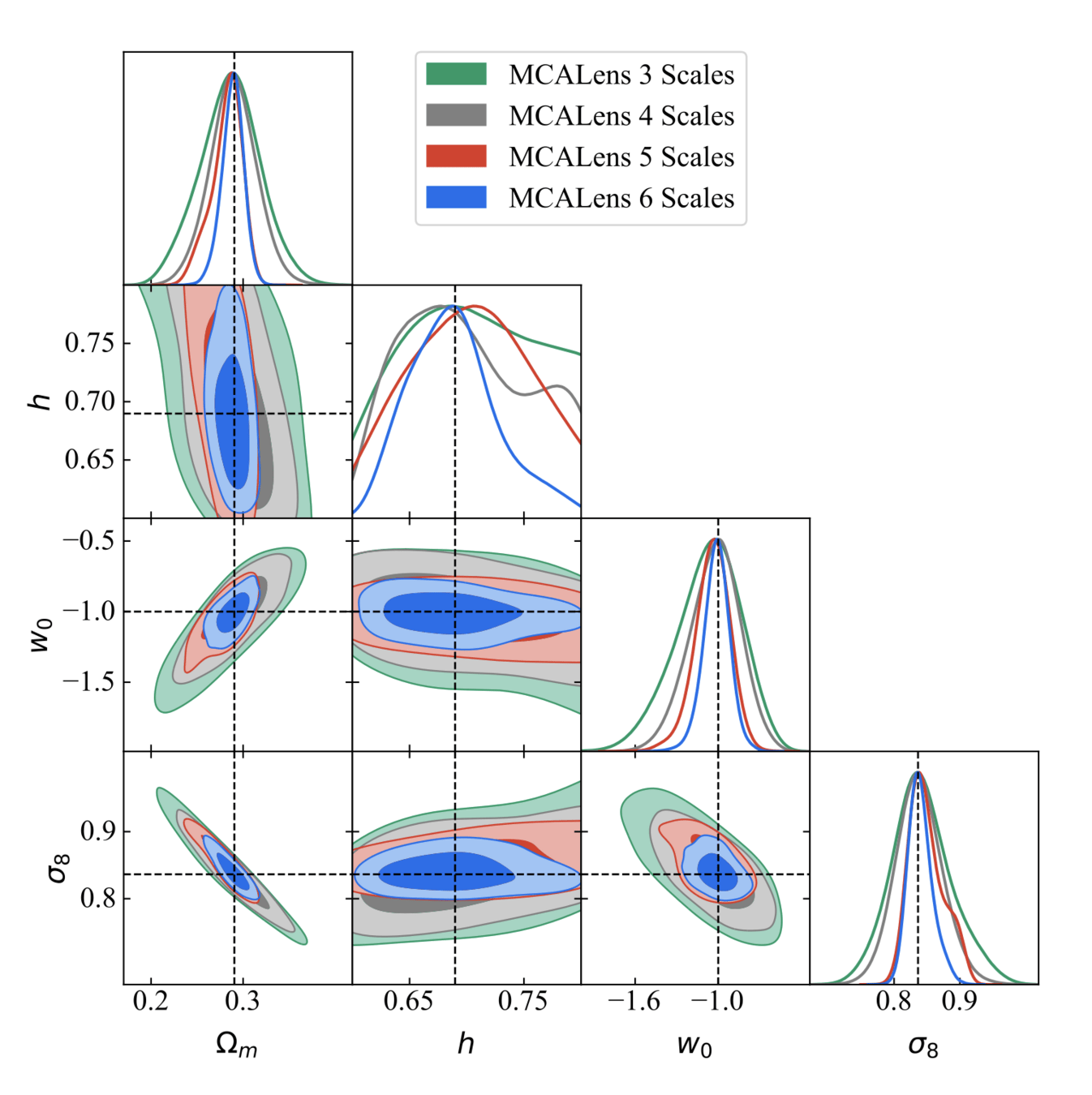
Results

Where does this improvement come from?

FoM improvement → 150%

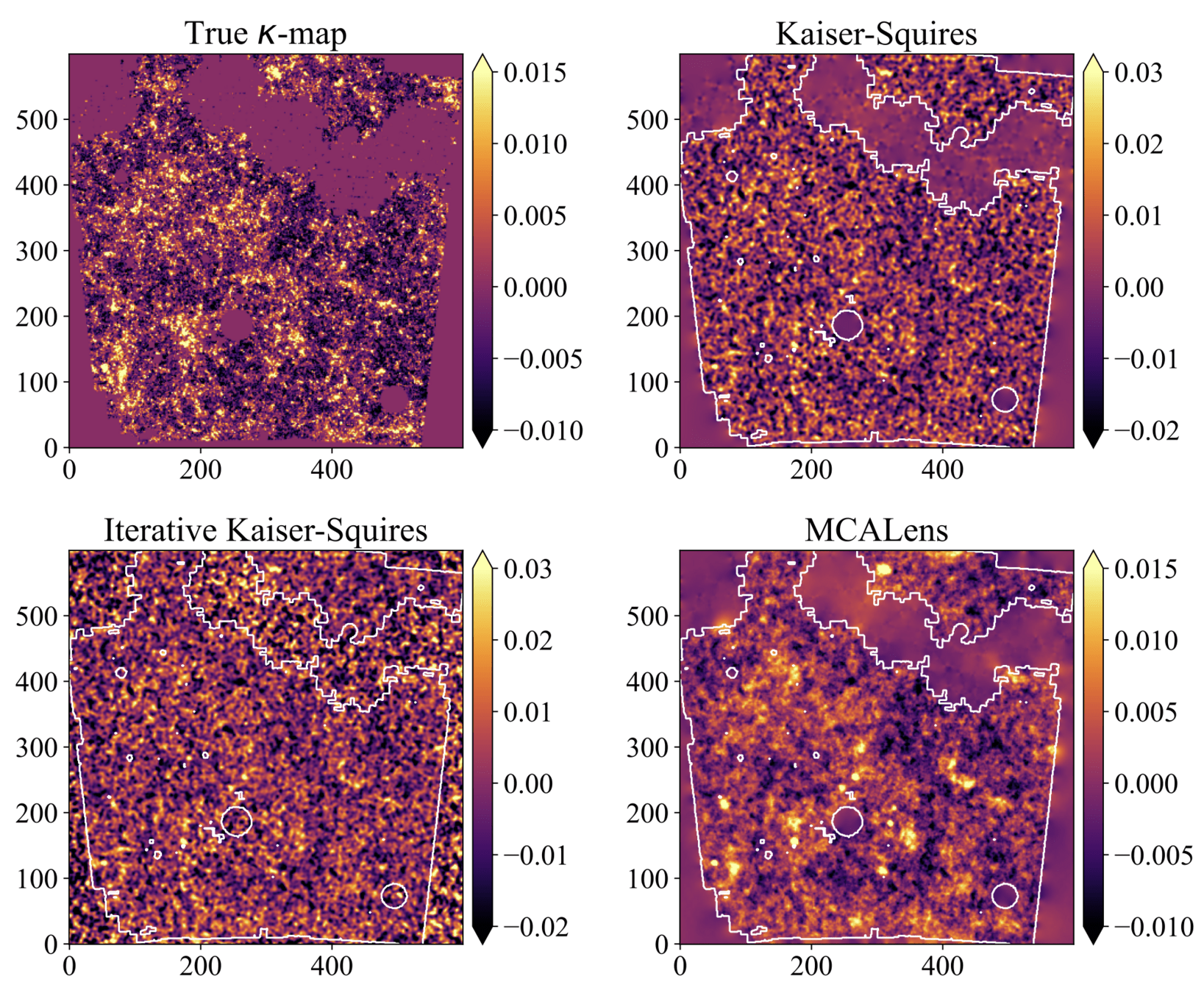
Plug-and-Play Mass Mapping with Uncertainty Quantification

Deep Learning for Mass Mapping?


Mass mapping method Type Accurate Flexible Fast rec. Fast UQ
Iterative Wiener Model-driven (Gaus. prior) ✗ ✓ ✓ ✗
MCALens Model-driven (Gaus. + sparse) ≈ ✓ ✗ ✗
DeepMass Data-driven (UNet) ✓ ✗* ✓ ✓
DeepPosterior Data-driven (UNet + MCMC) ✓ ✓ ✗ ✗
MMGAN Data-driven (GAN) ✓ ✗* ≈ ≈
What we'd like Data-driven ✓ ✓ ✓ ✓

Plug-and-Play Mass Mapping

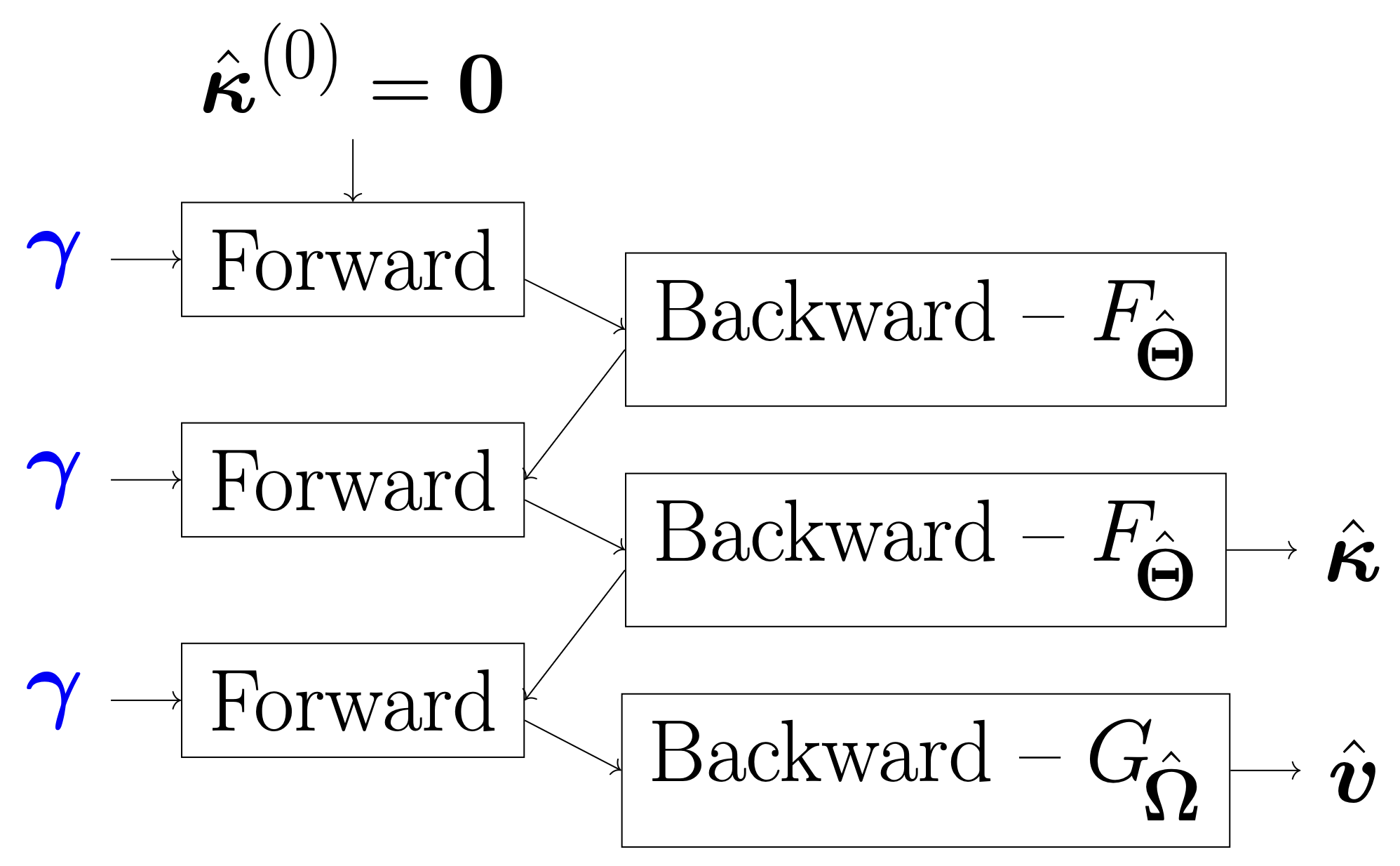
Instead of explicitly writing down a prior, we learn what a "likely" 𝜅 looks like from simulations and enforce it through denoising.

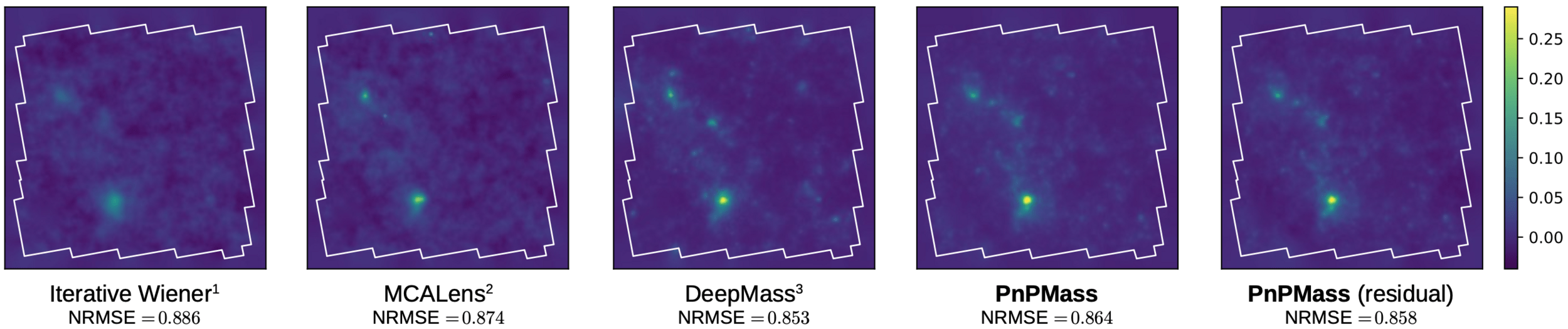
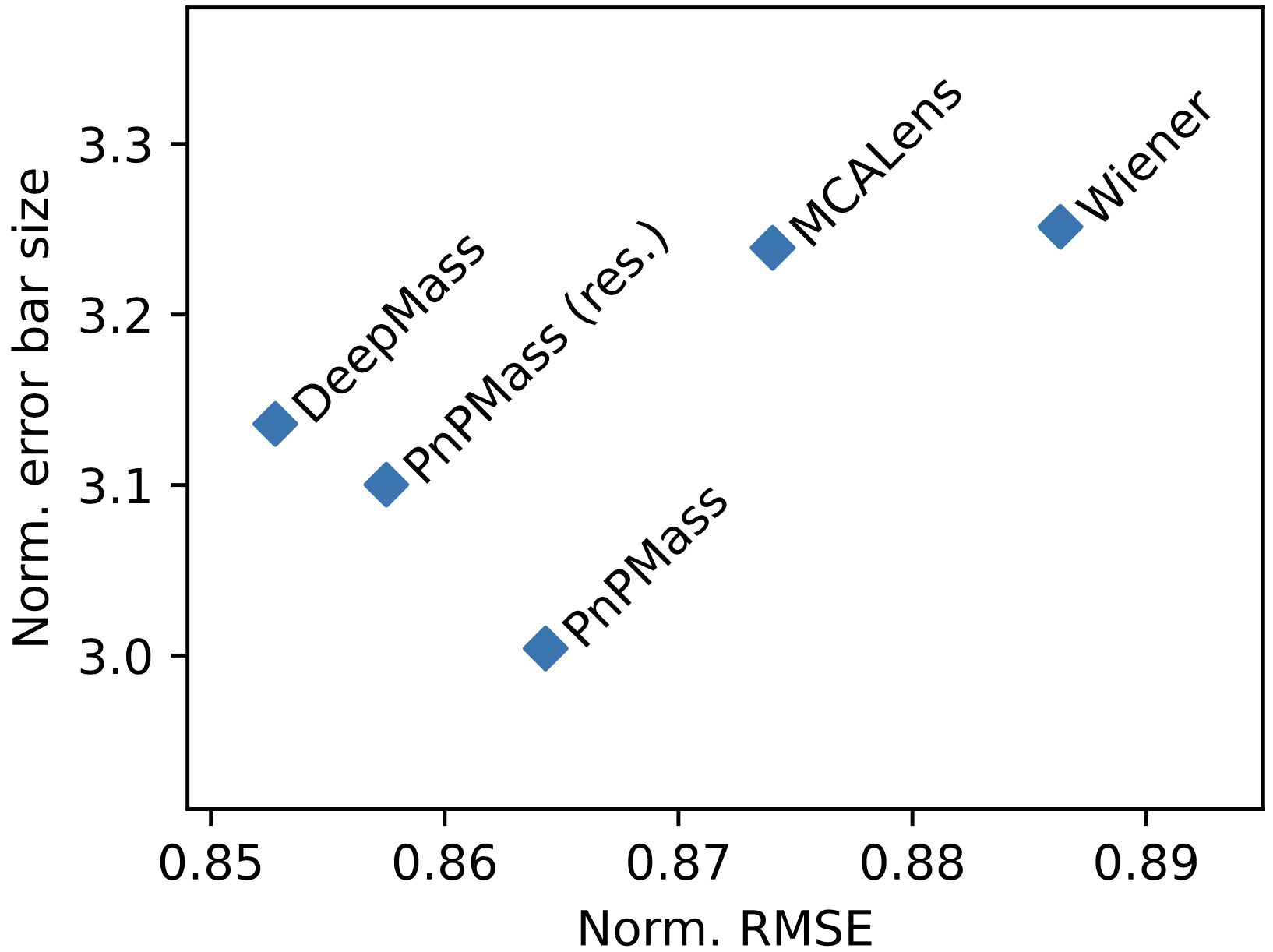
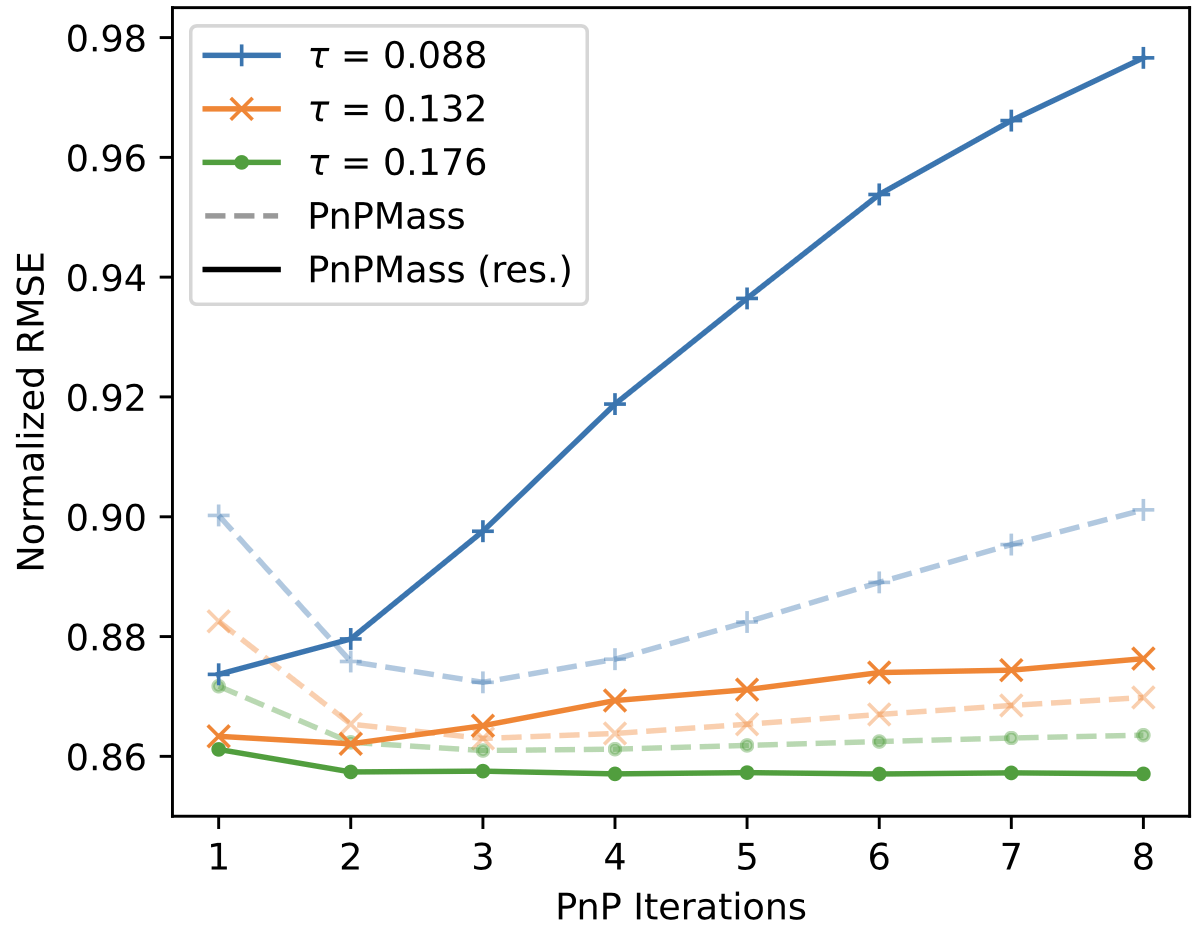
Results

Impact of baryonic effects on cosmology inference with HOS

Testing impact of baryonic effects on WL HOS

Idea - Explore two things:

  • Information content of summary statistics as a function of scale cuts & survey area
  • Testing the impact of baryonic effects on posterior contours

This will show:

  1. On what range of scales can the different statistics be used without explicit model for baryons
  2. Answer the question: how much extra information beyond the PS these statistics can access in practice

Baryonic effects

  • Effects that stem from astrophysical processes involving ordinary matter (gas cooling, star formation, AGN feedback)

  • They modify the matter distribution by redistributing gas and stars within halos.

  • Suppress matter clustering on small scales

  • Depend on the cosmic baryon fraction and cosmological parameters.

  • Must be modeled/marginalized over to avoid biases in cosmological inferences from WL.

Baryonic impact on LSS statistics

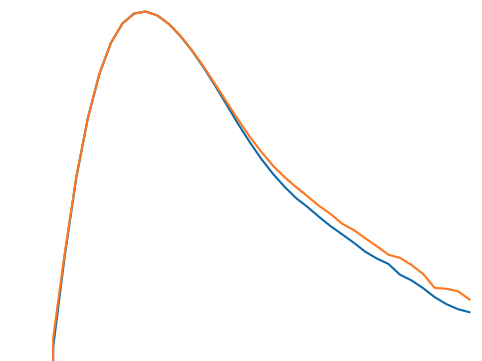
baryonic effects in P(k)

Credit: Giovanni Aricò

cosmoGRID simulations:

Power Spectrum

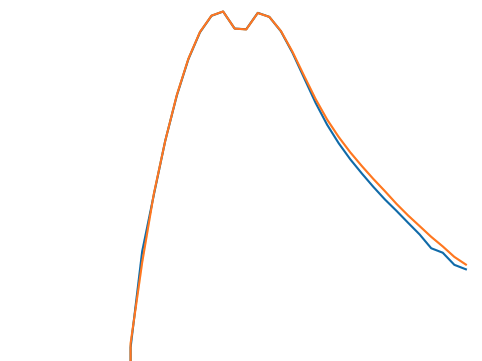
Wavelet l1-norm:  sum
of wavelet coefficients
within specific amplitude
ranges across different
wavelet scales

Wavelet peaks: local maxima of wavelet
coefficient maps

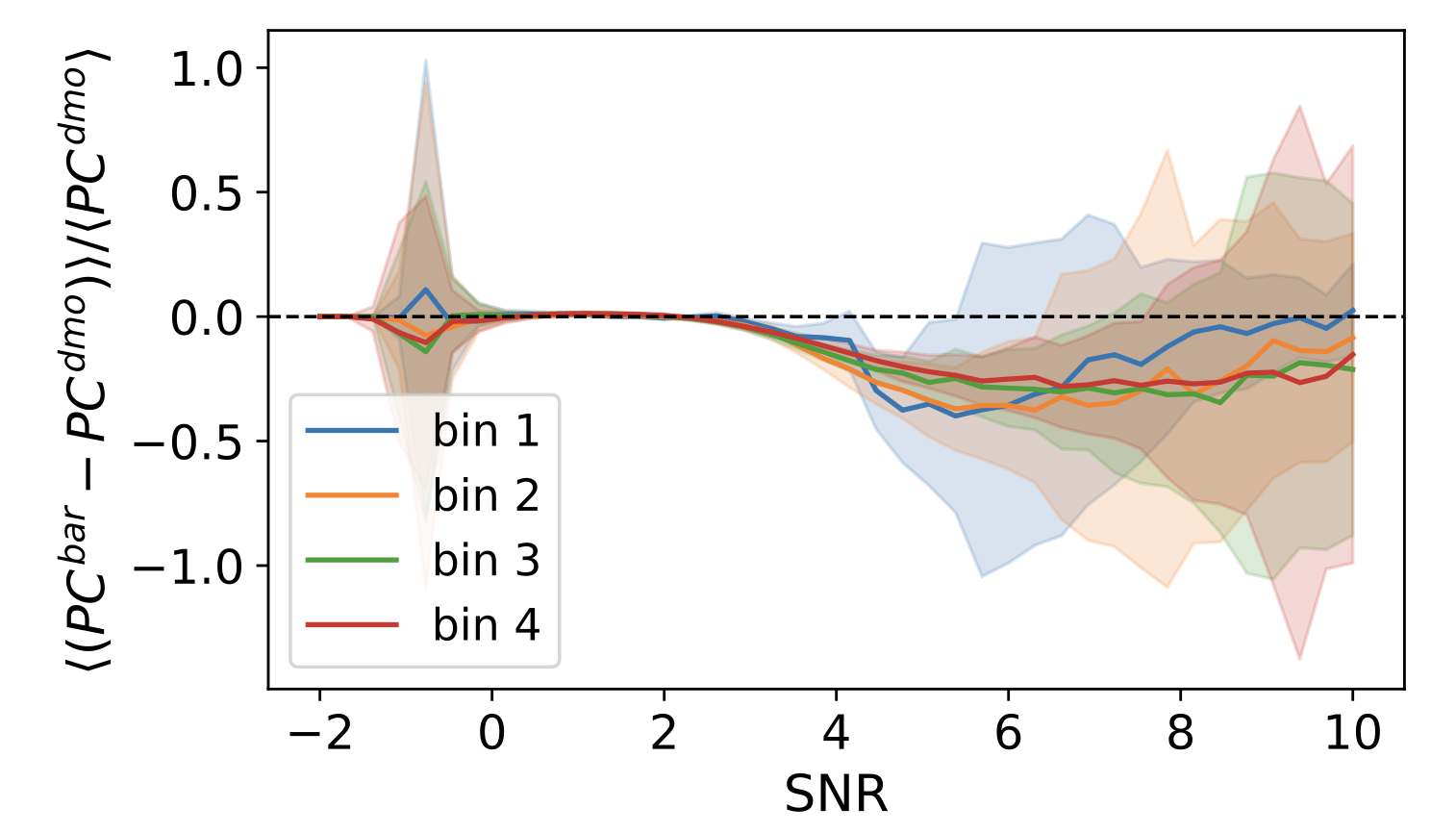
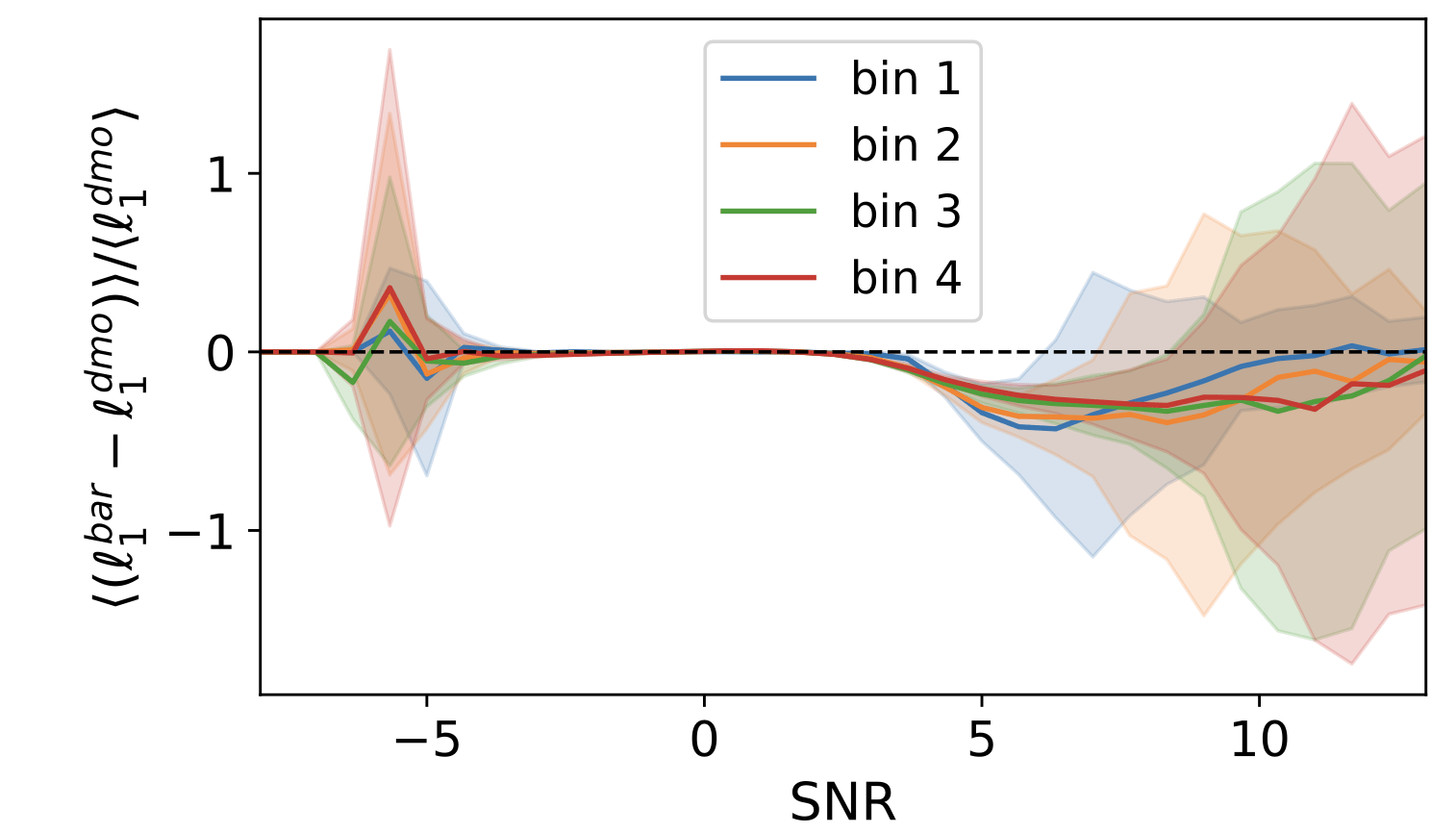
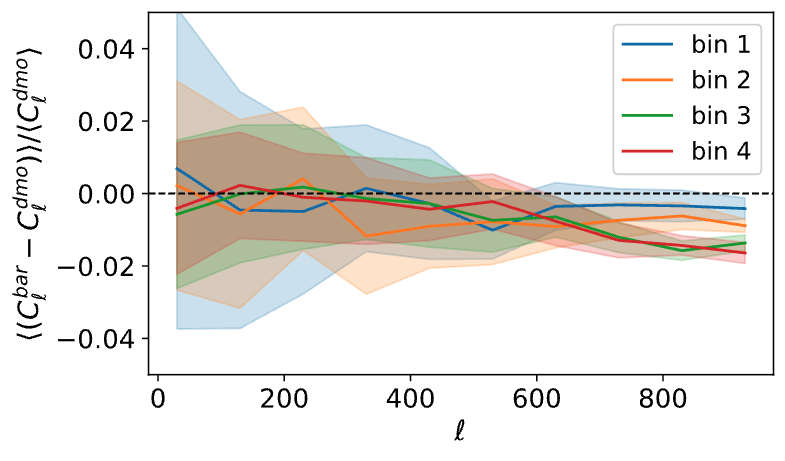
N-body sims, providing DMO and baryonified full-sky κ-maps from the same IC, for 2500 cosmologies. Baryonic effects are incorporated using a shell-based Baryon Correction Model (Schneider et. al 2019).

Inference method: SBI

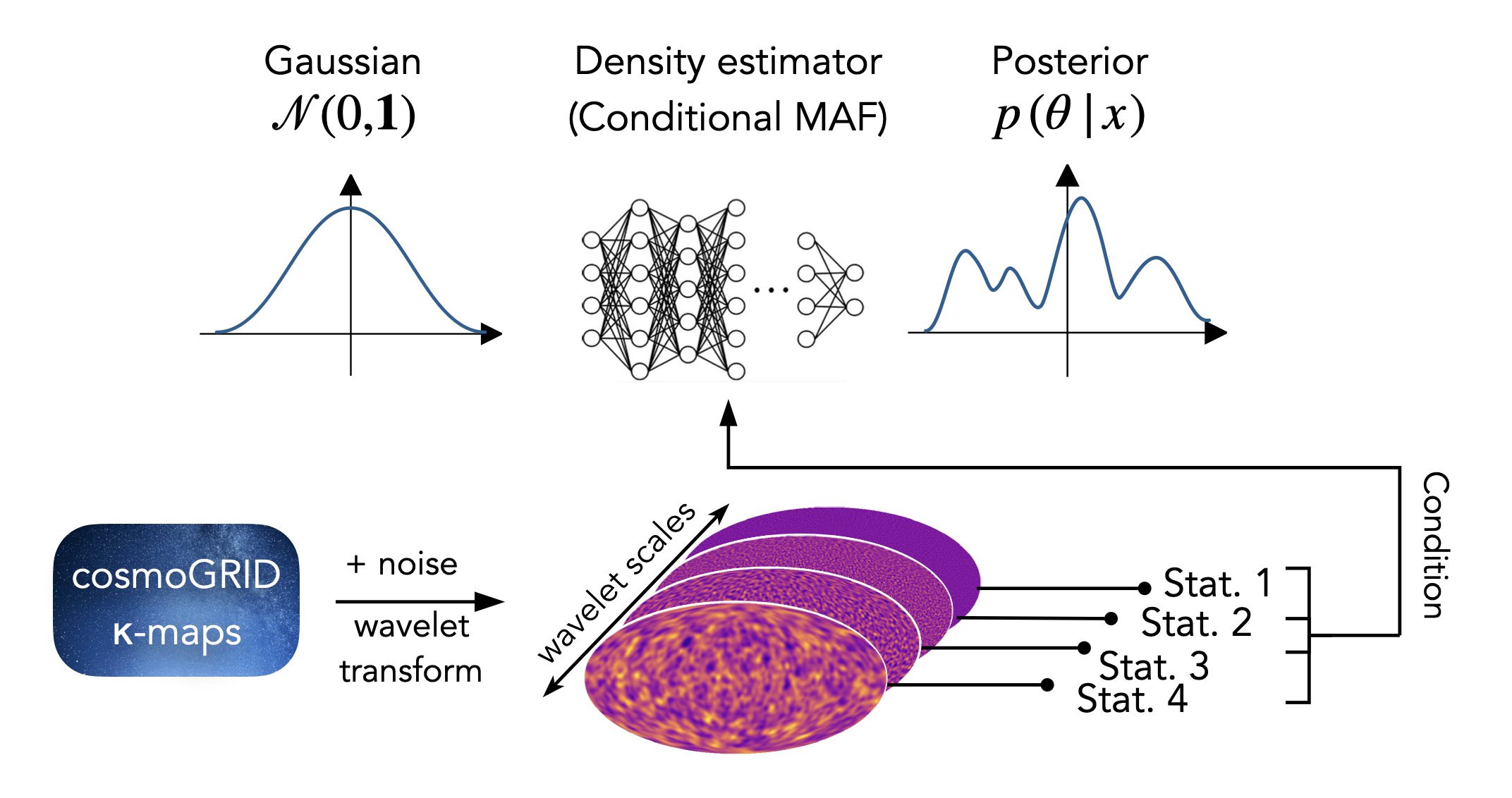
Training objective

\mathcal{L} = - \log p_\phi ( \theta | x )

Weak lensing tomography

Weak lensing tomography

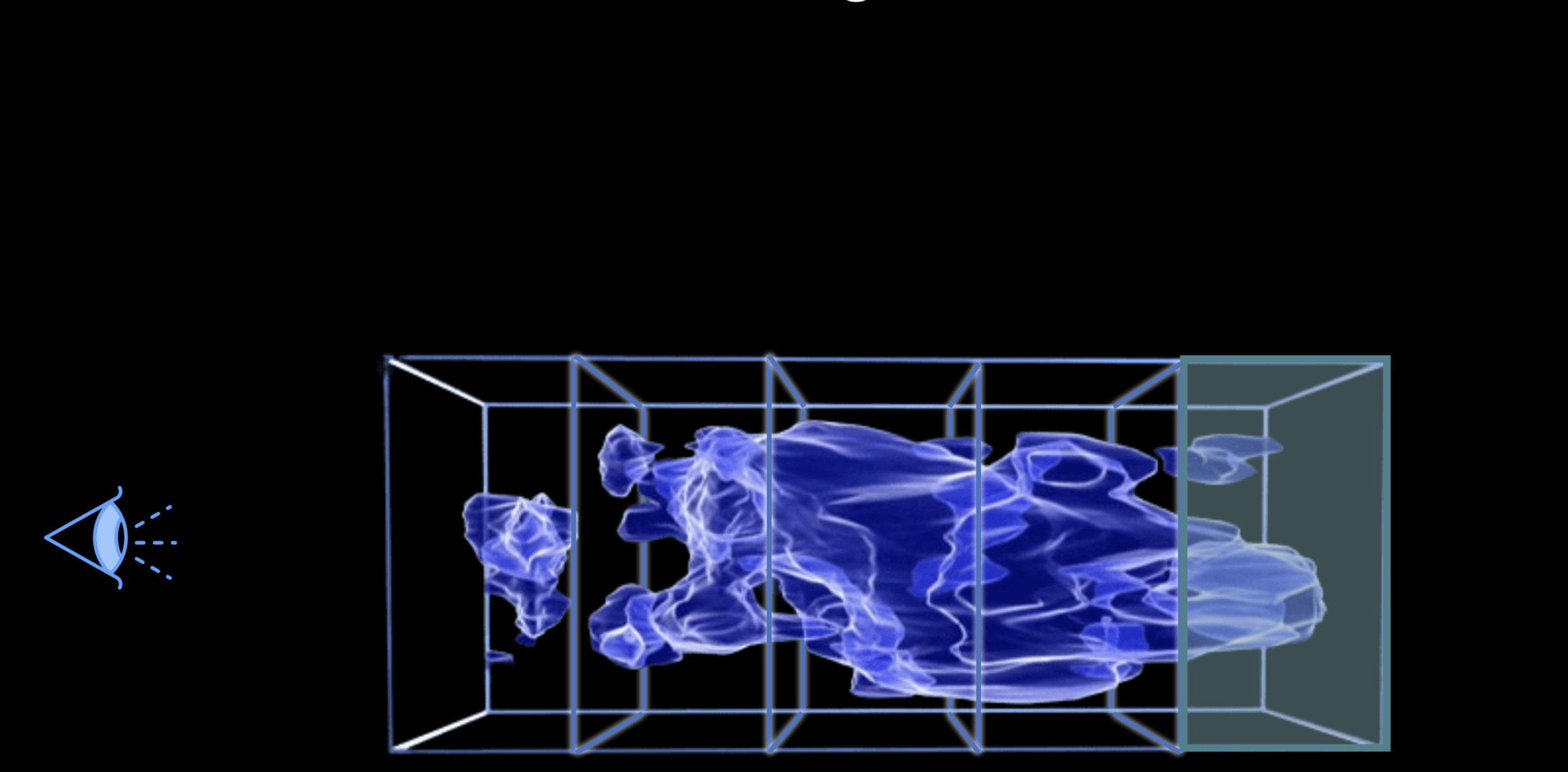
Weak lensing tomography

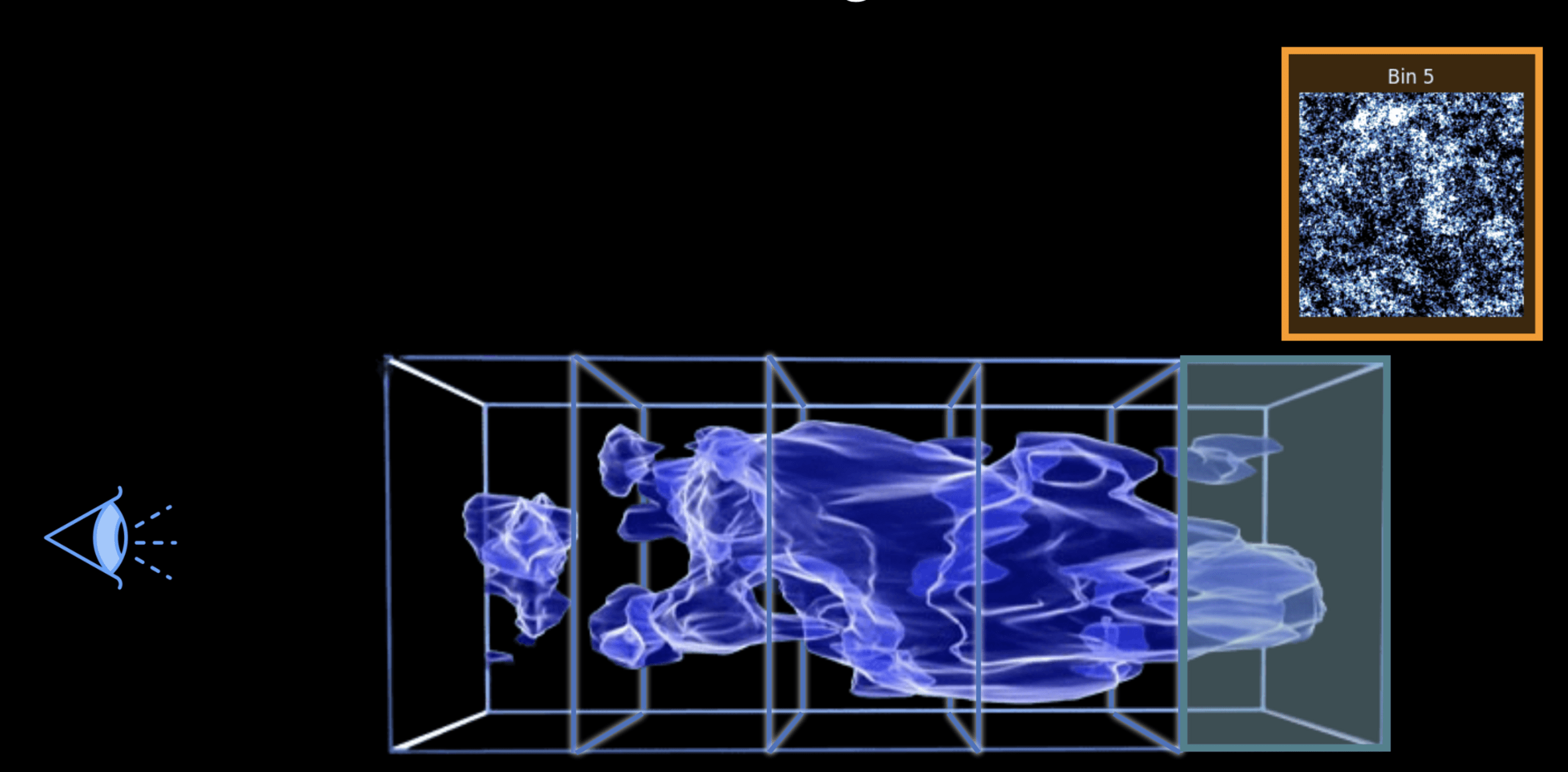
Weak lensing tomography

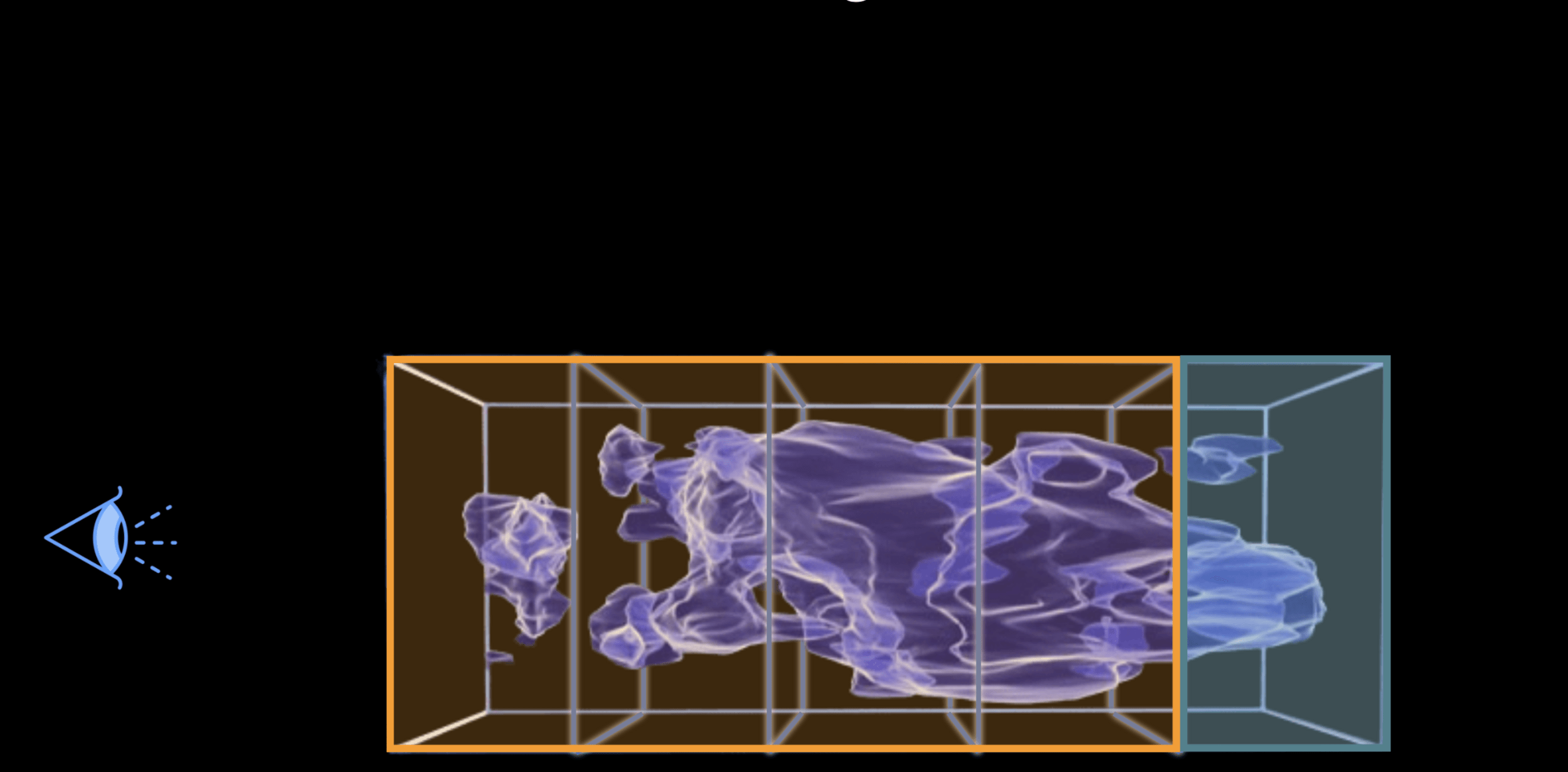
Weak lensing tomography

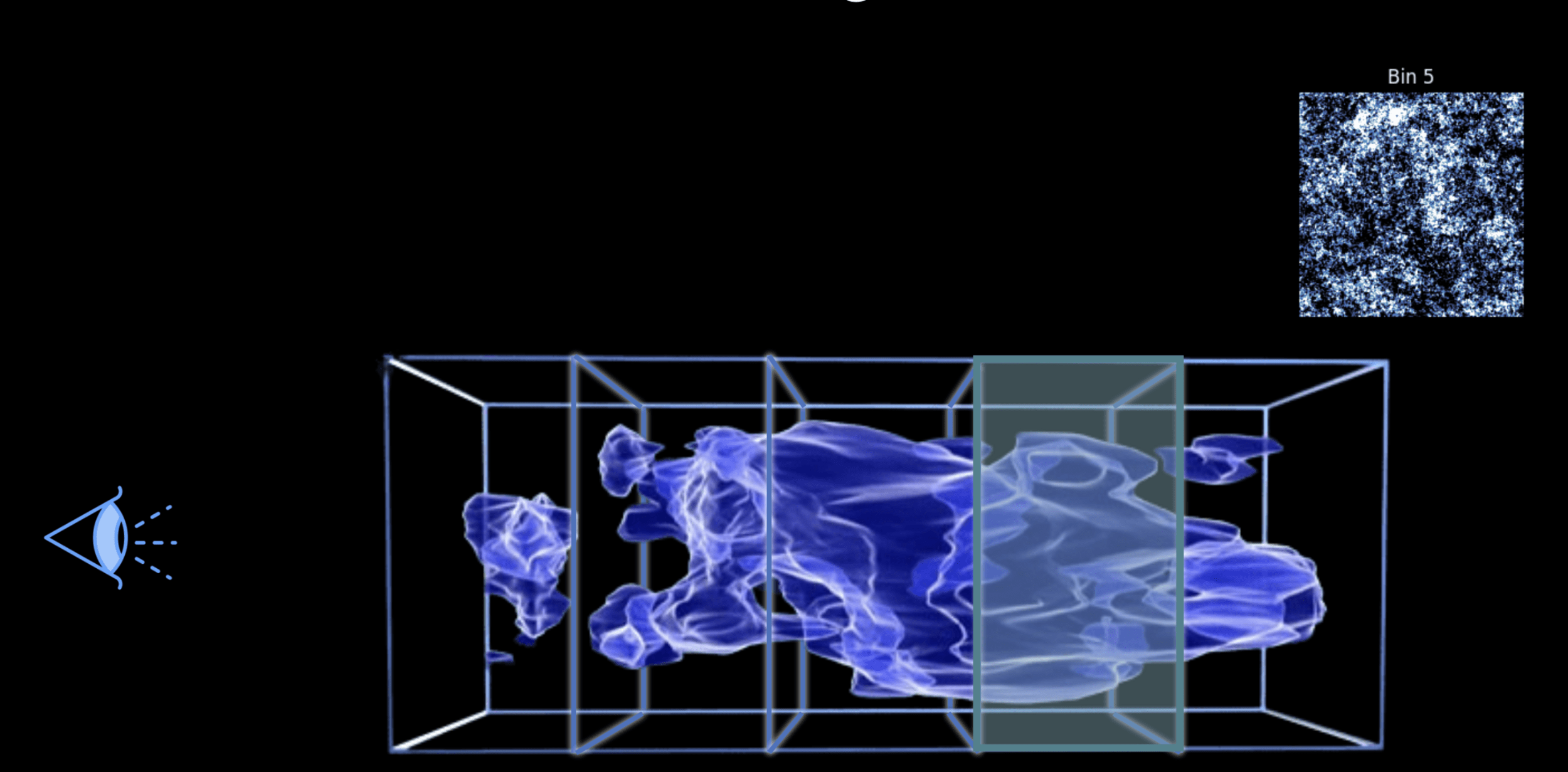
Weak lensing tomography

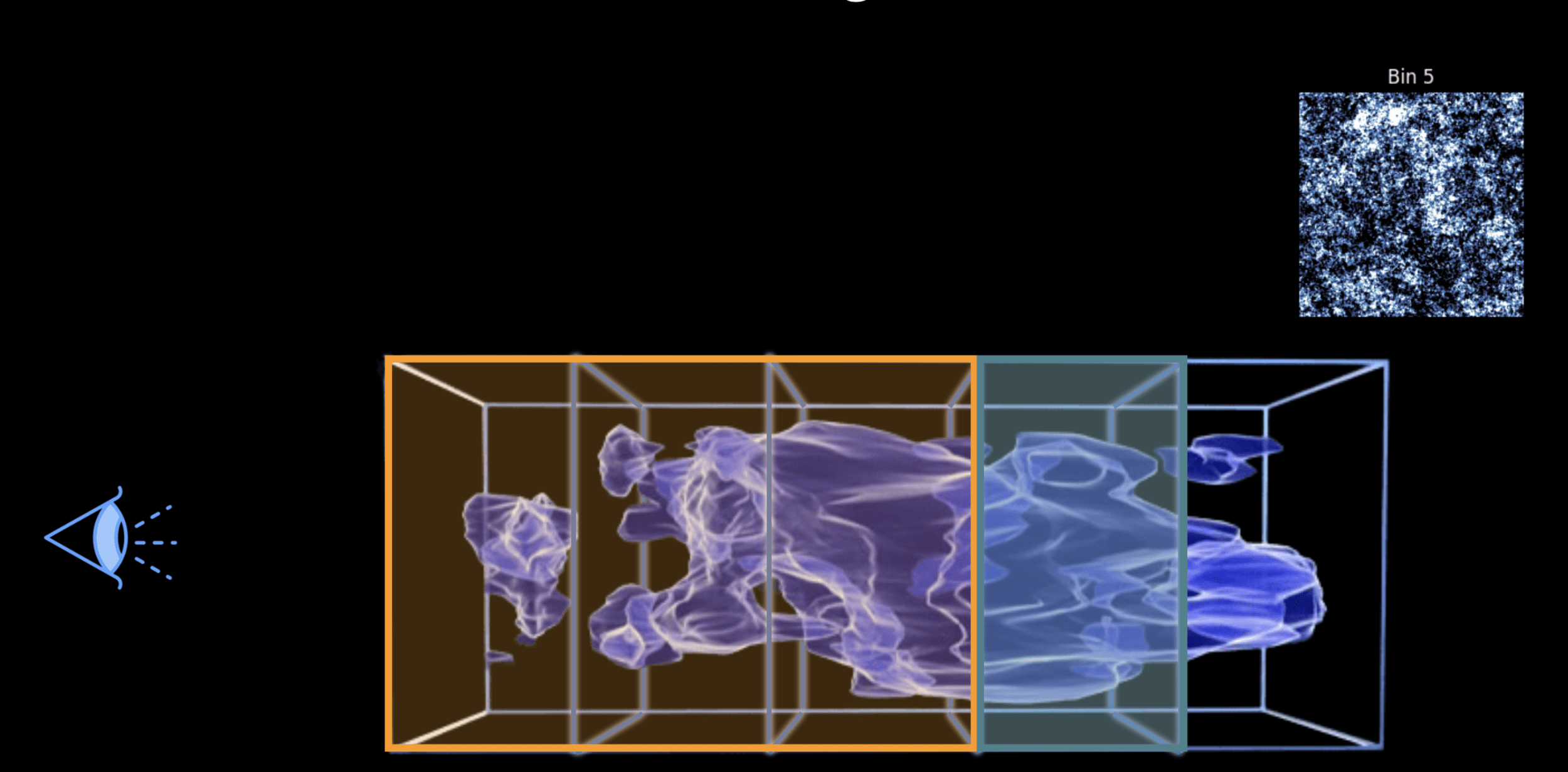
Weak lensing tomography

Weak lensing tomography

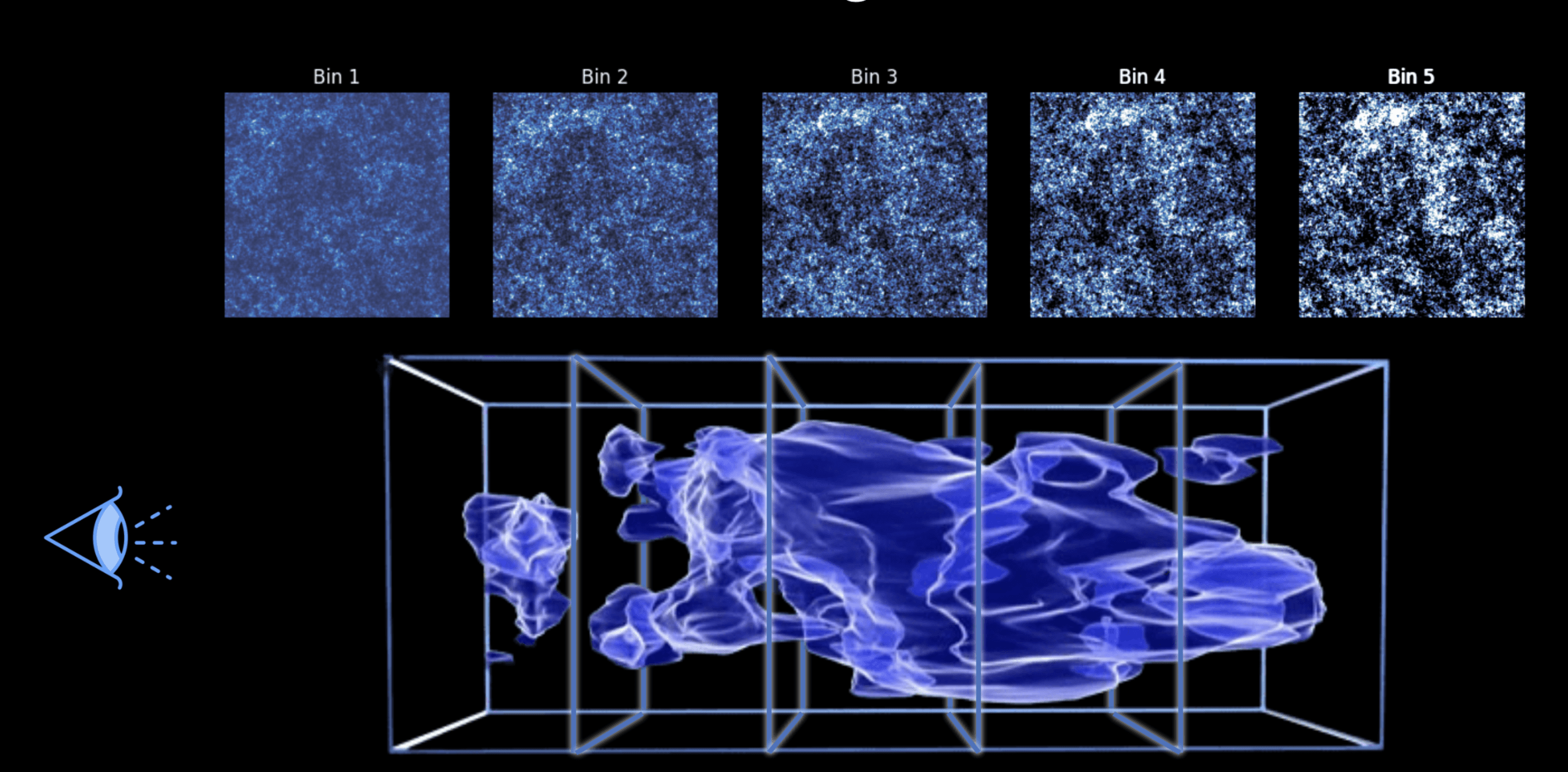
Weak lensing tomography

BNT transform

  • When we observe shear, contributions come from mass at different redshifts.
  • BNT Transform: method to “null” contributions from unwanted redshift ranges.
  • It reorganizes weak-lensing data so that only specific redshift ranges contribute to the signal.
  • BNT aligns angular (ℓ) and physical (k) scales.
  • This could help mitigate baryonic effects by optimally removing sensitivity to poorly modeled small scales and controlling scale leakage.

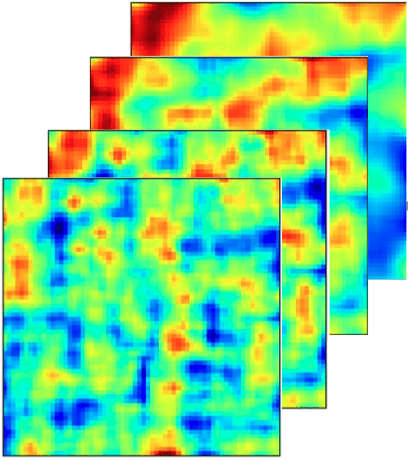
BNT maps

no BNT

BNT

How are statistics impacted?

Power Spectrum

l1-norm

* This could help mitigate baryonic effects by optimally removing sensitivity to poorly modeled small scales and controlling scale leakage?

The Scaling of Baryonic Bias with Survey Area

Determining Robust Scale Cuts

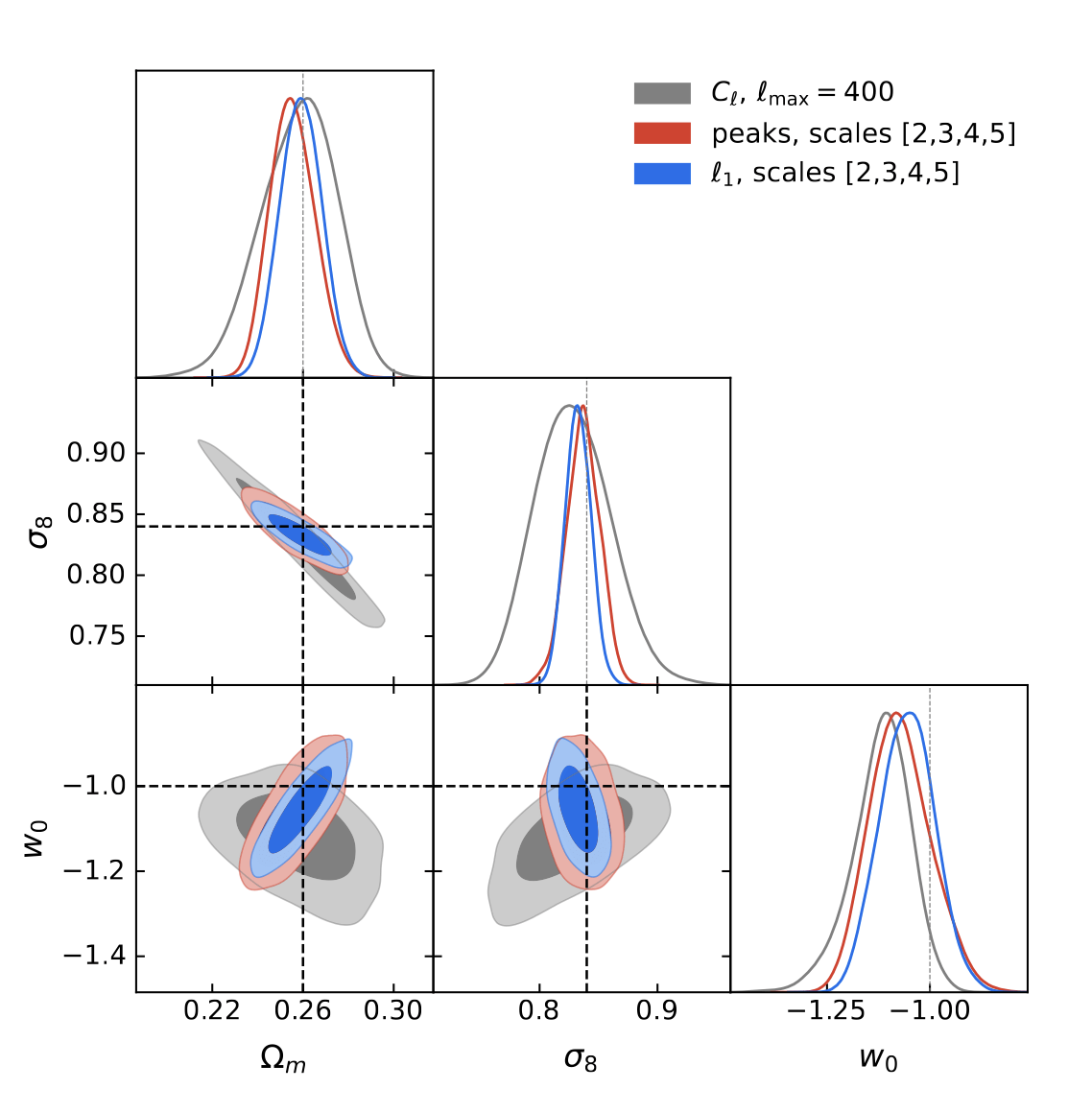
Information Content at Large Scales

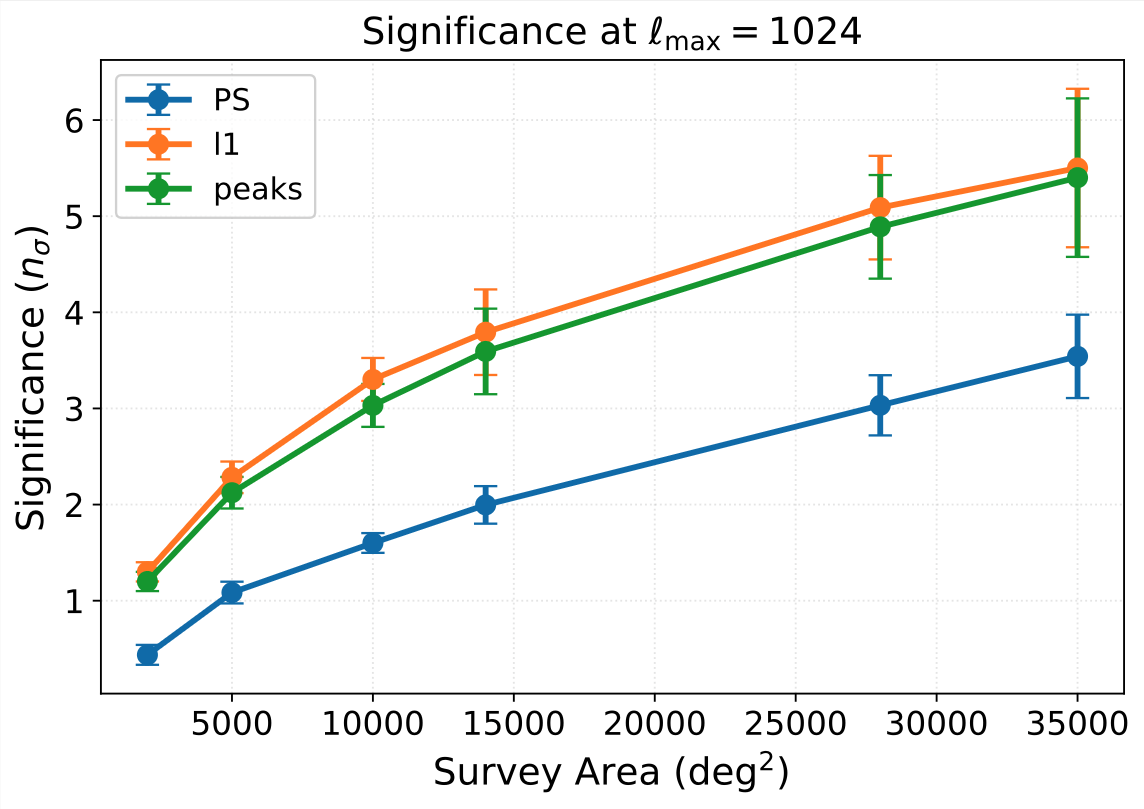
Results

+ Benchmarking Theoretical Wavelet l1-Norm Predictions Against Cosmological Simulations

+ Euclid Key Paper: DR1 analysis with theory-based HOS

Why Field-Level Inference?

Unifying Reconstruction, Systematics, and Cosmology

\delta_{\rm IC}
\gamma_{\rm Obs}

Explicit & Lossless

  • Zero Compression: Inference directly on the pixel-level data.

  •  FLI targets the full high-dim posterior.

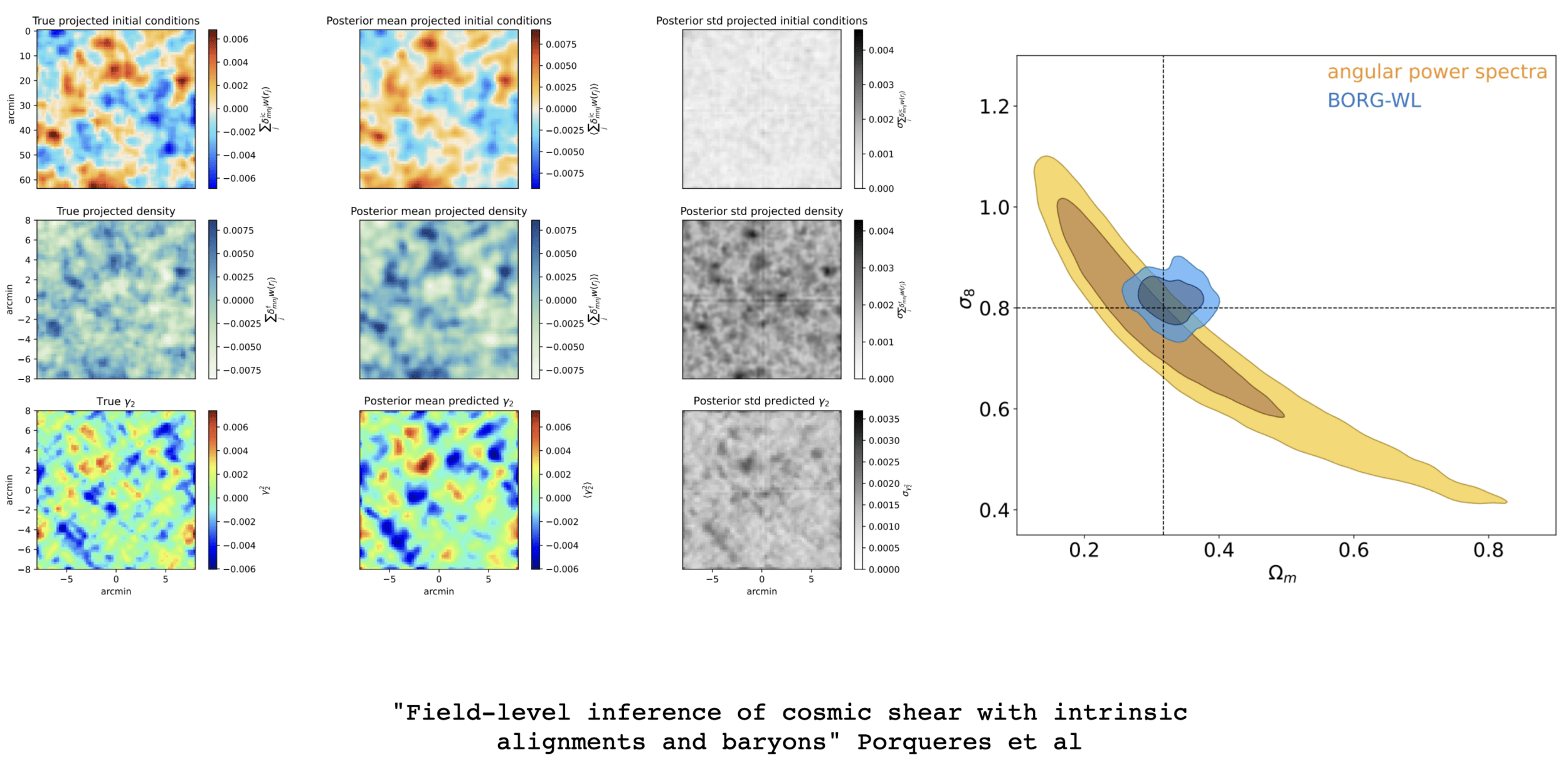
Digital Twin: Reconstructing ALL Latent Variables

  •  Beyond θcosmo reconstruct the entire formation history.

  • Initial Conditions (ICs)

  • Evolved DM Distribution

  • Peculiar Velocities

The FLI Advantage:

  • Self-Consistent Systematics: Modeling noise/masks + forward model other effects physically in 3D (cosmology + systematics become part of one model).

  • Validation: Posterior Predictive Tests & Cross-Correlations (e.g., kSZ, X-ray) without CV.

  • Discovery: A platform to test physics at the field level.

My background in Inverse Problems/WL Systematics/ SBI/ diff/ble programming/prob. DL + WL data provides the foundation needed to build these forward models.

FLI for Cosmic Shear

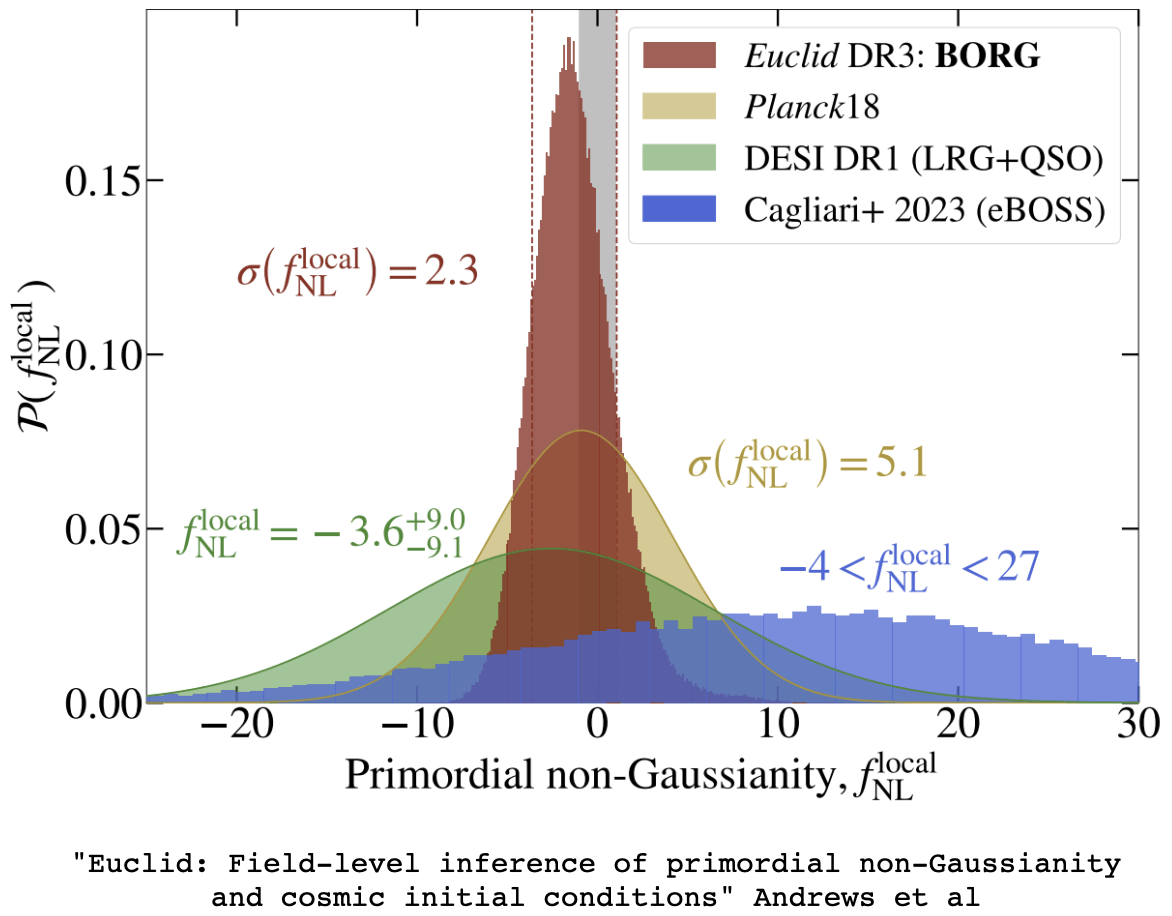
FLI for Primordial Non-Gaussianity

\theta_{\rm cosmo}
\theta_{\rm cosmo}
\theta_{\rm cosmo}

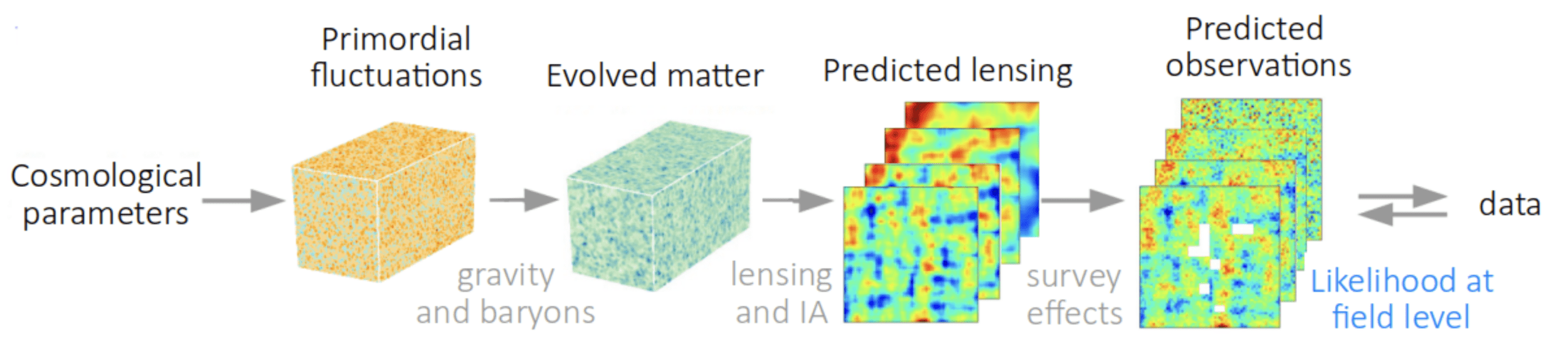
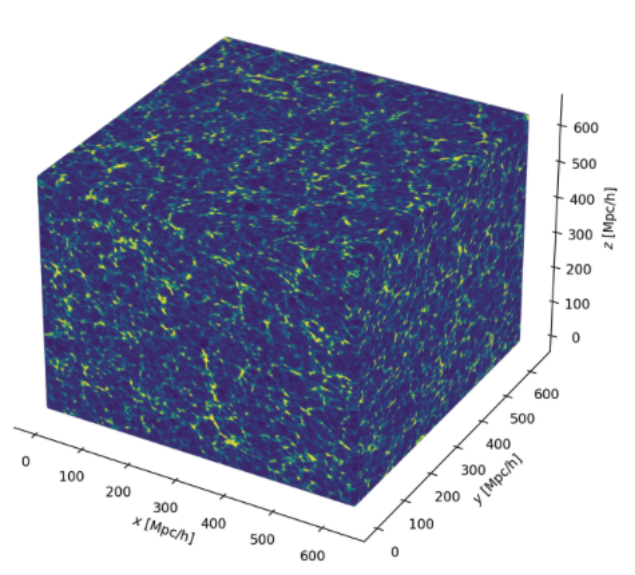
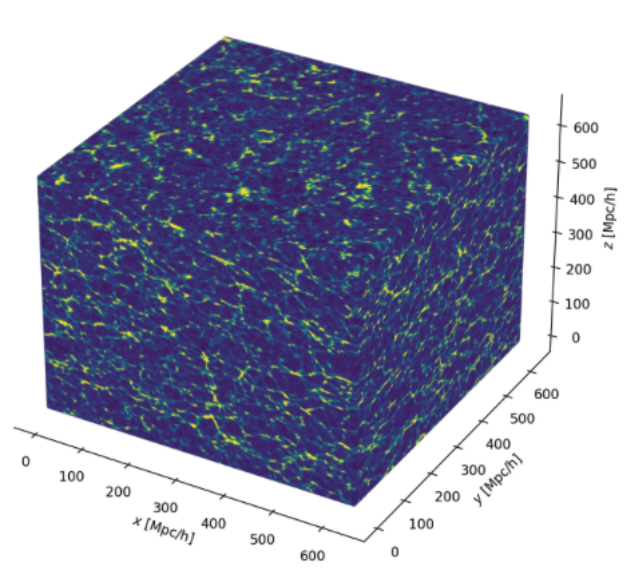
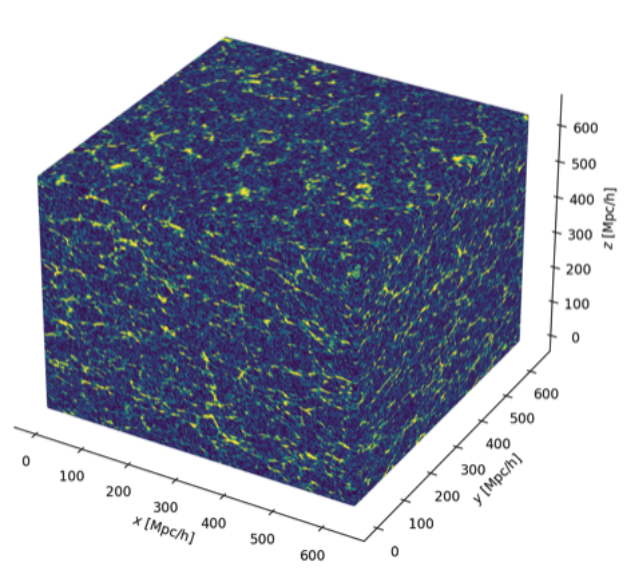
Gravity solver

Baryonification

Lensing+IA

Survey effects & systematics

Initial conditions

Evolved density

DM+baryons

Lensing maps

Predicted observations

Part 1: Gravity Solver

Goal: a differentiable, scalable gravity backbone that unlocks nonlinear information without bias.

Challenges:

  • Computational efficiency
    • Scale to Euclid/LSST volume (Gpc)
    • Resolve smaller (non-linear) scales (kpc)
  • Differentiability at scale: stable gradients for HMC, memory/communication
\}

Big dynamic range

Scalability + resolution → use fully non-linear, distributed (multi-GPU) PM simulations

Solution: A Hybrid Physical-Neural Approach

JaxPM + jaxdecomp + jax-healpy

3D domain decomposition and distributed FFTs

Use FNO instead

  • Performs global convolutions in Fourier space, learning the underlying continuous operator → learn effective Green’s function of the Poisson eqn from the data
  • Captures the non-local tidal deformations
  • Anisotropic: Can distinguish between different cosmic environments
  • Resolution Invariant: learned on small, high-res boxes → Zero-shot deployment on big lightcone mesh without retraining.

Computational efficiency

Resolution independence: Neural operators can generalize across resolutions after single-
scale training, facilitating multi-resolution analysis strategies

For field-level inference, we need correct velocities and displacement histories, not just final density fields. Therefore, the advanced version of my proposal is to implement Active Neural Force Correction. We inject the neural network inside the time-integration loop to correct the PM forces at every step.

  • Run Coarse PM, but at every time step, call an FNO to predict the "Residual Force" (Exact Force - PM Force) and kick the particles.

  • FNO learns the mapping
    between function spaces (the density field 𝜌 to the displacement potential 𝜓 )

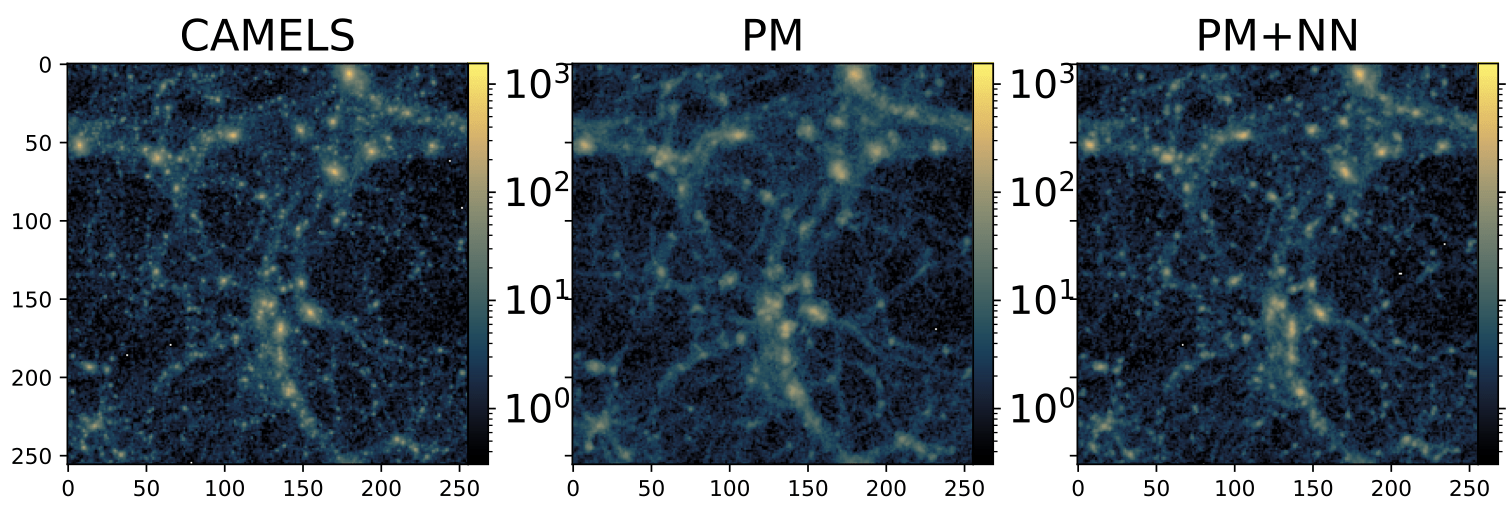
F_\theta(\mathbf{x}, a)=\frac{3 \Omega_m}{2} \nabla\left[\phi_{P M}(\mathbf{x}) * \mathcal{F}^{-1}\left(1+f_\theta(a,|\mathbf{k}|)\right)\right]
​"Hybrid Physical Neural ODEs for Fast N-body simulations" Lanzieri, Lanusse, Starck

PM solvers still face a resolution bottleneck

(mesh grid → smooths out gravity)

Strategy: inject neural correction into time-integration loop to recover small scales

Learned Isotropic Fourier Filter

predict the complex 3D force field from density, instead of just modifying potential

cannot correct anisotropic non-linearities or phase errors

\theta_{\rm cosmo}

Gravity solver

Baryonification

Lensing+IA

Survey effects & systematics

Initial conditions

Evolved density

DM+baryons

Lensing maps

Predicted observations

Part 2: Baryon Modeling

Challenge:

  • More accurate modeling of baryons beyond simple thermodynamics
  • Scalable/Fast enough for FLI + differentiable

In BORG-WL → EDG

  • Displaces particles to minimize enthalpy assuming a simple polytropic eqn of state.
  • It cannot create features that don't exist in the potential (e.g., AGN bubbles, non-local feedback effects).

Flow-Matching Conditional Optimal Transport

  • The Bridge: Evolve directly from DM → Gas.
  • Learns the optimal transport map from gravity solver output to hydro density fields.
  • Captures non-linear feedback morphology that simple EOS models may miss.
  • Reproduces the correct HOS of the gas distribution.

Adjoint Sampling

  • Adjoint Sensitivity Method (solving the ODE backward).

  • Reduces gradient memory cost.

  • Feasible HMC sampling on 3D grids.

Baryon Emulator

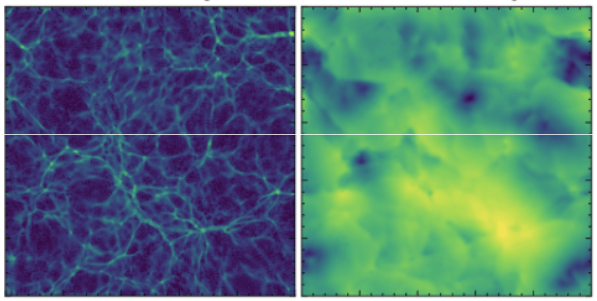
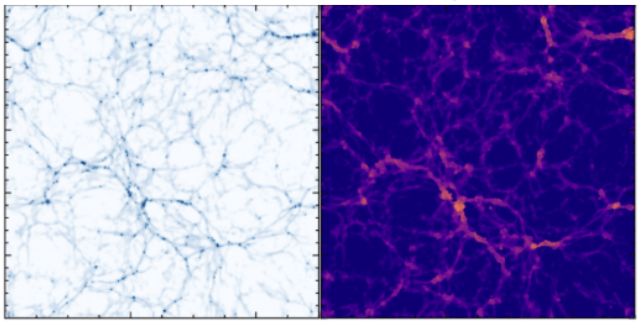
PM Density

Velocity

Density

Temperature

"BaryonBridge: Interpolants models for fast hydrodynamical simulations" Horowitz et al. 2025

Sampling methods

\theta_{\rm cosmo}

Gravity solver

Baryonification

Lensing+IA

Survey effects & systematics

Initial conditions

Evolved density

DM+baryons

Lensing maps

Predicted observations

Part 3: Field Level Systematics

Exploiting Phase Information to Distinguish Physics from Artifacts → Euclid realism

  • In power spectra, systematics often mimic cosmological signals.

  • In the 3D field, they possess distinct spatial signatures.

  • By differentiating through the forward model, the inference engine uses phase information to separate signal from noise.

  • Inject systematics directly into the pipeline:
    • ​IA → TATT
    • Spatially varying shear bias and survey depth
  • Survey Geometry

  • Photo-z:

    • BHM to sample n(z) and marginalise over redshift uncertainties, using forward model of the photometric fluxes

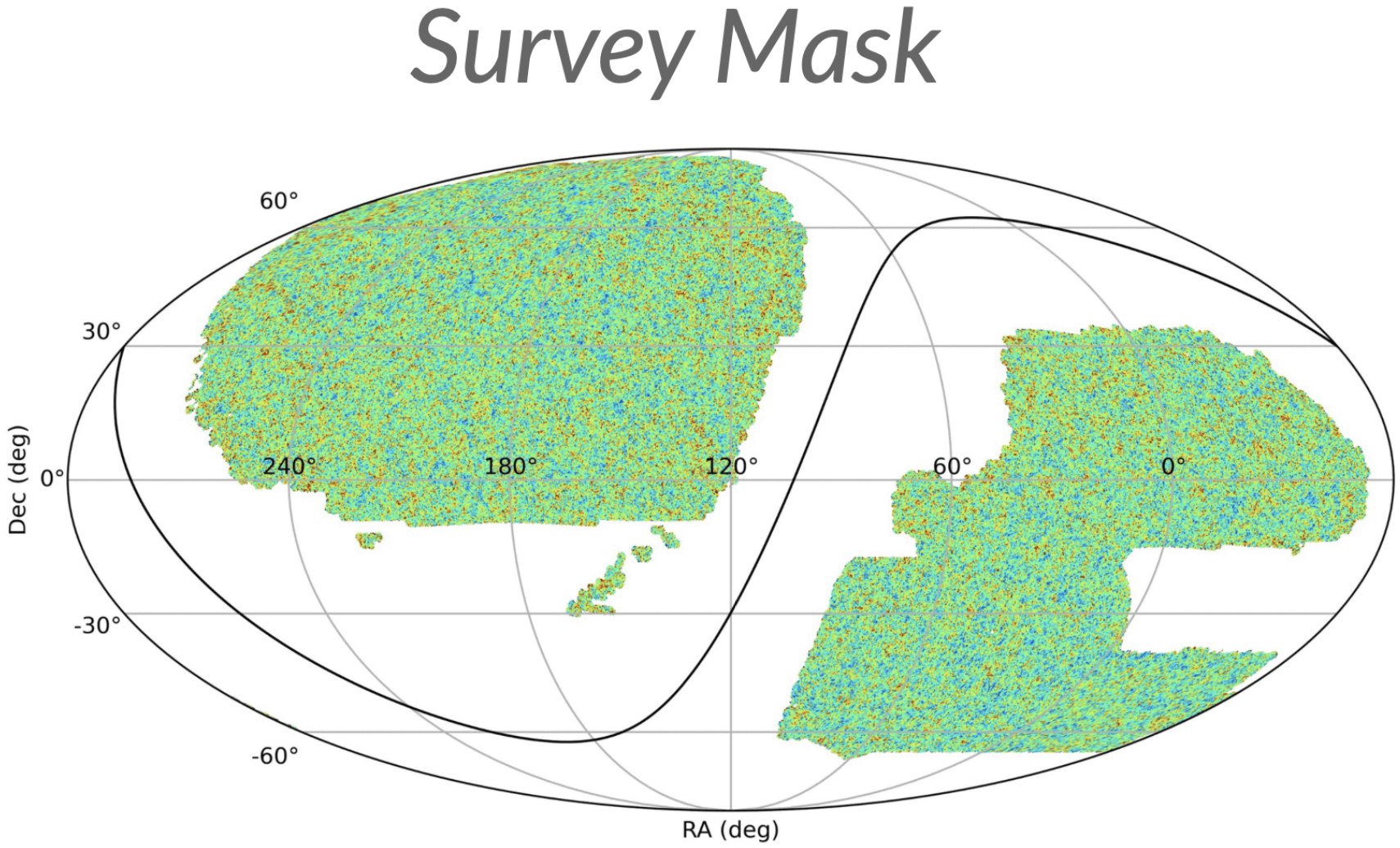
Part 4: Validation and Scientific Discovery

Challenge: No Clear Baseline

  • Power spectra are necessary but not sufficient.

  • First step → use HOS

  • No standard "baseline" in the literature for field-level accuracy.

  • Validation must move from statistical to mechanistic.

Test: "Do We Get the Positions Right?"

  • Input: Euclid Weak Lensing (Shear) → Reconstructed DM Field.

  • Posterior Predictive Checks:

    • Individual Objects: Turn specific clusters/voids into cosmological probes.

    • Cross-Correlation: Check alignment with tSZ/X-ray/CMB lensing.

    • If our reconstruction places a massive halo at (x,y,z), X-ray telescopes should see hot gas there.

Discovery & Survey Design

  • Cosmic Variance Cancellation: Inferred ICs → Deterministic prediction of all other observables.

  • Targeted Follow-Up: Use the Digital Twin to guide observations.

  • Survey Optimization: Use the reconstructed field to design optimal masks or scan strategies for future follow-ups.

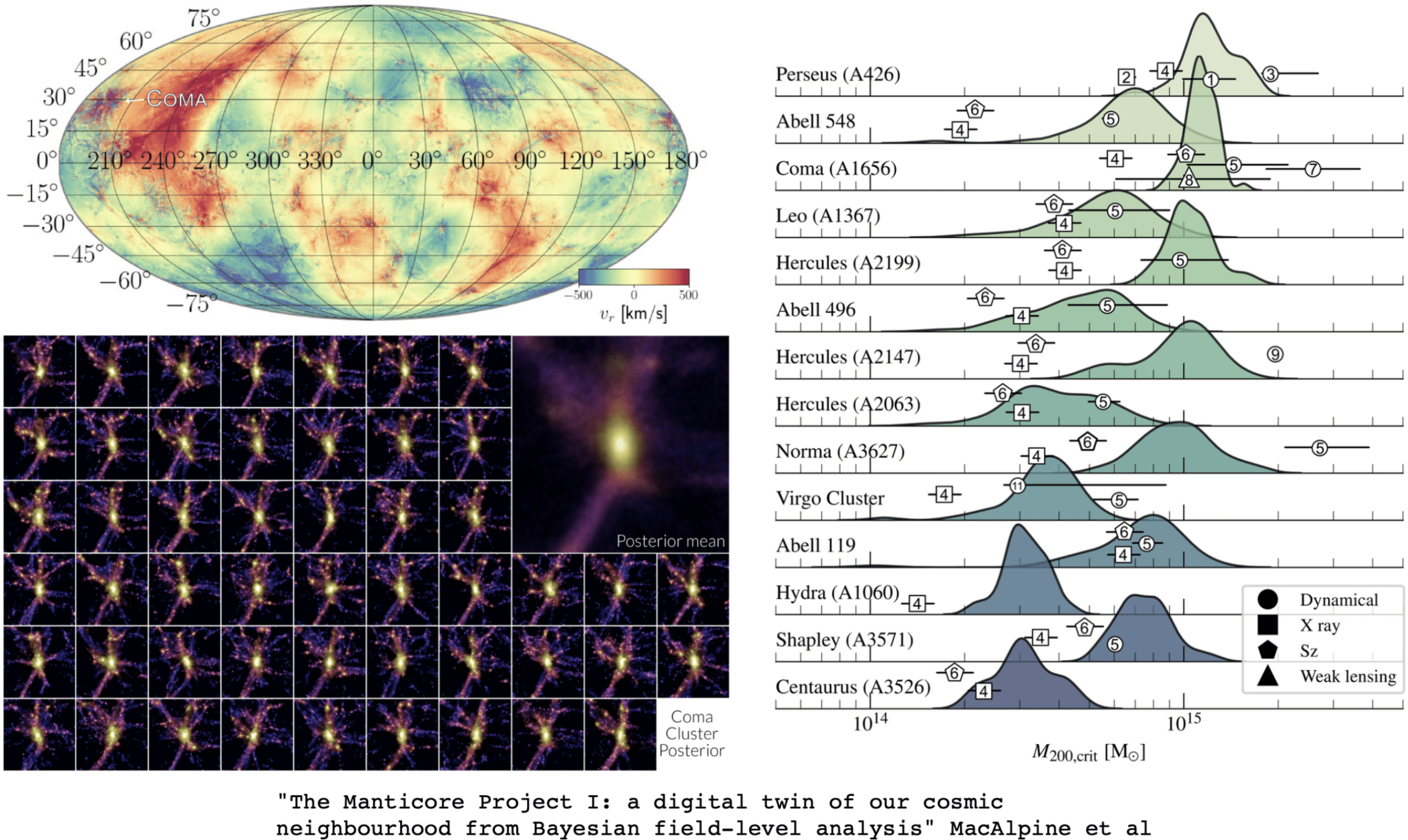
The Local Universe without CV

Lensing with JaxPM

JAX-Based Full Field forward model :

  • What has been done so far :

  • A fully differentiable and distributed matter only simulator using JaxPM and jaxDecomp

  • An accurate Born lensing and spherical projection that can produce convergence maps from particle mesh snapshot

  • A distributed probabilistic forward model that can be sampled with a big simulation

TODOS:

  • Have a first test on mock convergence maps with a distributed 8 GPUs forward model

  • Integrate s2fft in the pipeline to go to shear maps

Made with Slides.com