Ridiculous Operations in log(n) with Treaps
Ankit Sultana
June 4, 2021
Background
Heaps
insert(elem)
max() / min()
extract_max() / extract_min()


Binary Search Trees
search(elem)
delete(elem)
insert(elem)
max()
min()
lower_bound()
upper_bound()
BSTs
search(elem)
insert(elem)
remove(elem)
max()
min()
lower_bound(value)
upper_bound(value)
Binary Search Trees
search(elem)
delete(elem)
insert(elem)
max()
min()
lower_bound()
upper_bound()
BSTs
insert(elem)
search(elem)
remove(elem)
max()
min()
lower_bound()
upper_bound()
kth_smallest(k)
count_less_than(value)

Treaps
- Cartesian Tree: A tree with two keys in every node, such that the tree forms a BST on one key and a Heap on the other.
- Treap: A cartesian tree where the heap keys are random
Treap
This is a valid Treap, with two keys per node. The orange set of keys forms a BST and the green set forms a Min-Heap
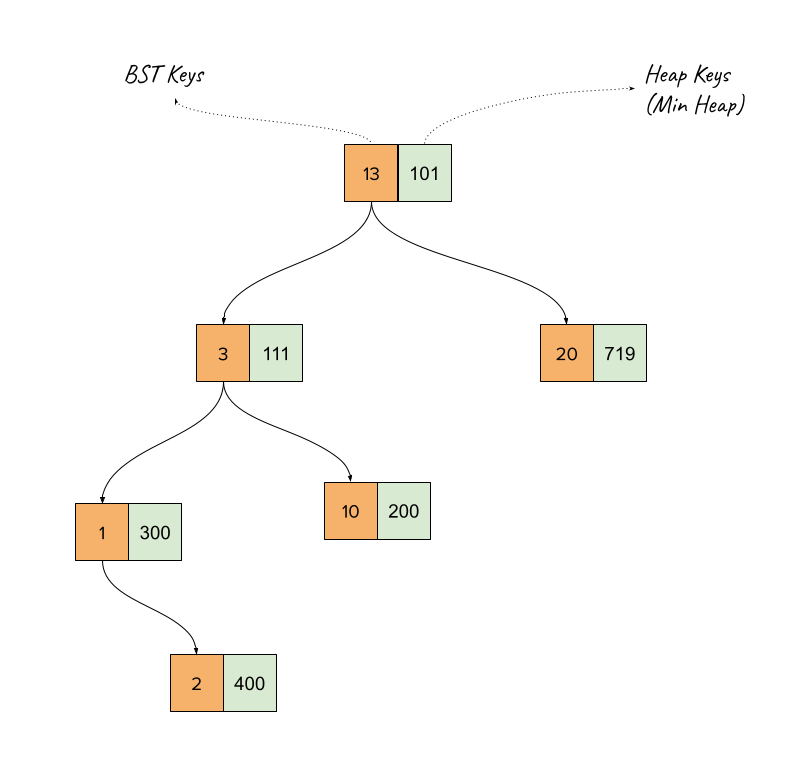
Treap
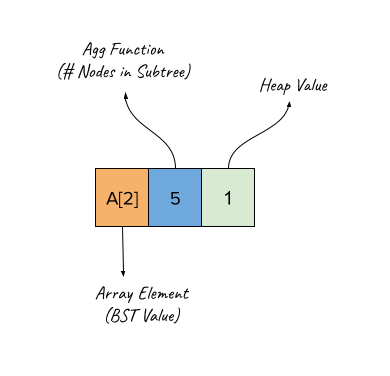
Same Treap which tracks number of nodes in the sub-tree in each node

Treap
search(elem)
insert(elem)
delete(elem)
min()
max()
lower_bound(value)
upper_bound(value)
kth_smallest(k) /kth_largest(k)
count_less_than(value)

What Else Can I Do With Treaps?
Treaps can be used to represent "dynamic arrays":
Get Element at Index
Delete Element at Index
Insert Element at Index
Range Min/Max/Sum
Reverse Sub-Array
Transplant Sub-Array
Split Array / Merge Two Arrays
etc.
Main Treap Operations
Merge(Treap_1, Treap_2): This takes in two treaps, such that all BST values in Treap_1 are less than all BST values in Treap_2, and combines them.
Split(Treap, v): Creates two treaps from the input Treap, such that all values in one treap are <= v, and all the values in the other are > v
Merge Treap

Merge Treap

Merge Treap

Merge Treap
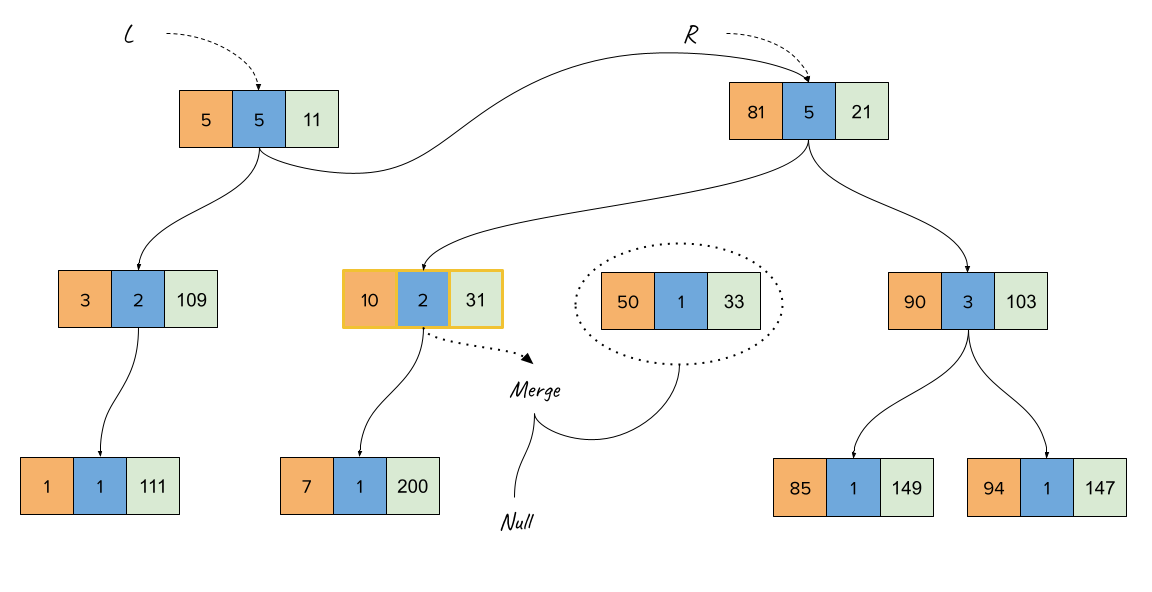
Merge Treap

Merge Treap

Implicit Treap
Treaps where the BST value is not explicitly stored
Allows the dynamic array operations discussed before
Relies on the fact there's a unique labelling for a BST with N nodes for labels in [1, N]
An array with N elements has unique indices
Implicit Treap
Relies on the fact there's a unique labelling for a BST with N nodes for labels in [1, N]
Implicit Treap
Relies on the fact there's a unique labelling for a BST with N nodes for labels in [1, N]
4
2
1
3
5
Implicit Treap
4
3
2
5
1
1
2
3
4
5
Treap T = new Treap(A[1]);
for (int i = 2; i <= 5; i++) {
T = Merge(T, new Treap(A[i]))
}Implicit Treap
4
3
2
5
1
1
2
3
4
5
4
1
103
3
1
49
Implicit Treap
4
3
2
5
1
1
2
3
4
5
4
1
103
3
2
49
2
1
70
Implicit Treap
4
3
2
5
1
1
2
3
4
5
4
1
103
3
3
49
2
1
70
5
1
11
Implicit Treap
4
3
2
5
1
1
2
3
4
5
4
1
103
3
3
49
2
1
70
5
4
11
1
1
84
Implicit Treap
4
3
2
5
1
1
2
3
4
5
4
1
103
3
3
49
2
1
70
5
5
11
1
1
84
Implicit Treap
4
3
2
5
1
4
1
103
3
3
49
2
1
70
5
2
11
1
1
84
1
2
3
1
2
Implicit Treap
4
3
2
5
1
4
1
103
3
2
49
2
1
70
5
2
11
1
1
84
1
1
2
1
2
Implicit Treap
4
3
2
5
1
4
1
103
3
2
49
2
1
70
5
2
11
1
1
84
1
1
2
1
2
Implicit Treap
4
3
2
5
1
4
1
103
3
5
49
2
1
70
5
3
11
1
1
84
1
2
3
4
5
Implicit Treap
4
3
2
5
1
4
1
103
3
5
49
2
1
70
5
3
11
1
1
84
1
2
3
4
5
R
Implicit Treap
4
3
2
5
1
4
1
103
3
5
49
2
1
70
5
3
11
1
1
84
1
2
3
4
5
R
R
Implicit Treap
4
3
2
5
1
4
1
103
3
5
49
2
1
70
5
3
11
1
1
84
1
2
3
4
5
R
R
R
Implicit Treap
Allow us to represent an array, with modification operations like:
insert/delete an element at any index
append an array to another
split an array into two
reverse a subarray
transplant a subarray
...
Implicit Treap
Allow us to represent an array, with read operations like:
get element at index
get sum/min/max of values for indices in [l, r]
get k-th smallest value in [l, r]
...
Persistent Implicit Treaps
All operations of Implicit Treaps with
*full immutability*
After each modification operation, a version is created, and each version is always accessible
Persistent Implicit Treaps - Merge
...
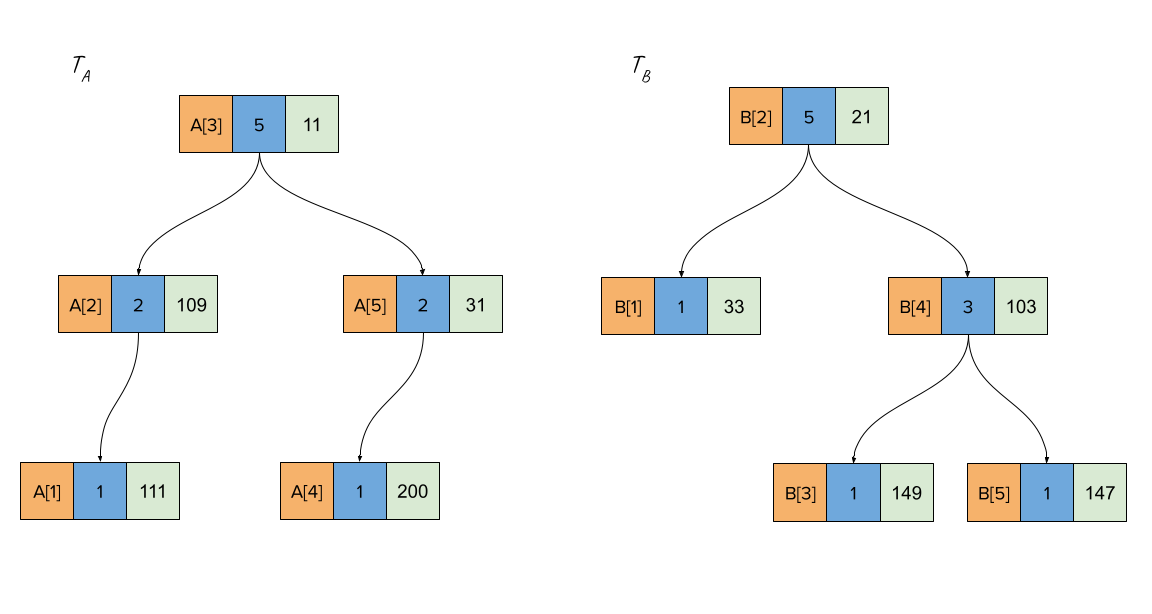
...

...

...

...
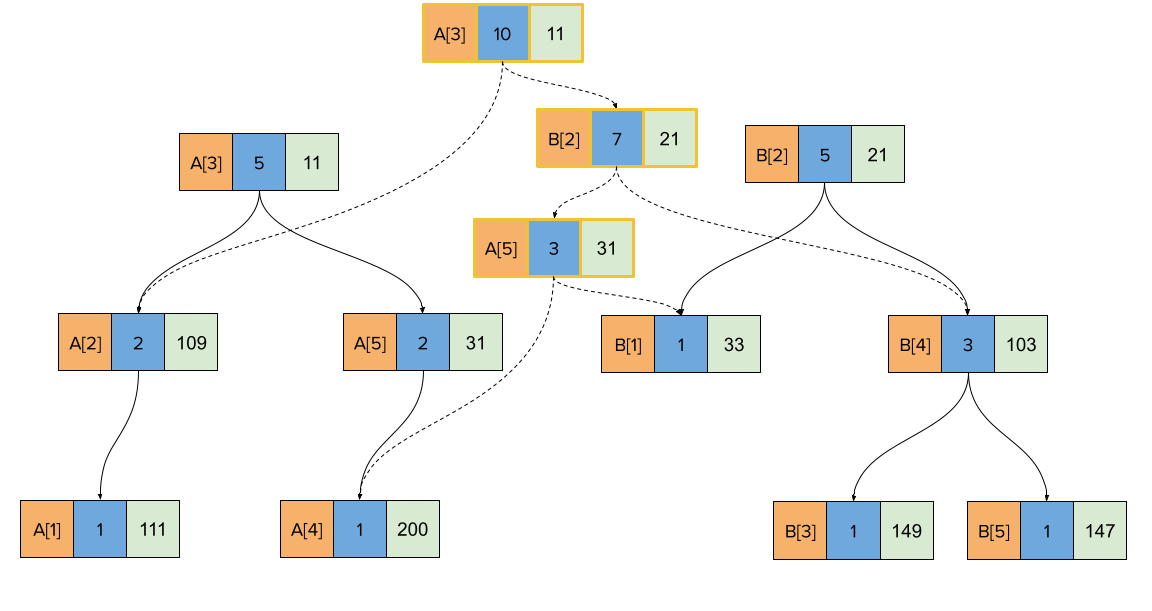
Persistent Implicit Treaps
All operations of Implicit Treaps with
*full immutability*
After each modification operation, a version is created, and each version is always accessible
Persistent Implicit Treaps
After each modification operation, a version is created, and each version is always accessible
When arrays A and B are merged to yield C, you can still perform any of the read-operations on all of A, B and C.
Other Data Structures
Splay Trees
Segment Trees (aka Interval Trees)
Binary Indexed Trees (aka Fenwick Trees)
Sparse Table
Fibonacci Heaps
...