Map Projection
Content
- Map Projection
- Class/Category
- Distortion
- CRS
- Types
- Identifier
- 4326 VS 3857
- Difference
- Best Practice
What is Map Projection?
Map projection is a way to represent
a 3D globe into a 2D map.
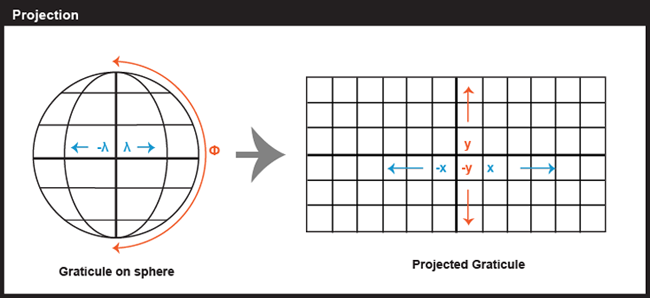
Map projection can be described in many ways, usually by their CLASS or DISTORTION.
Map projection at a glance...
Map Projection: CLASS
3 main classes of a map projection.

Planar
Conic
Cylindric
Map projection: DISTORTION
All map projections will distort map.
Distortion types are based on 4 (four) 3D globe properties:
- Equivalence (Area)
- Conformality (Shape)
- Equidistance (Distance)
- Azimuthality (Direction)
*Any map projection @ 2D map can only fully maintain 1 or 2 of the 3D globe properties.
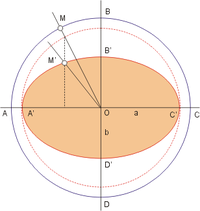
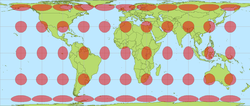
Info: Tissot Indicatrix
If no distortion occurs, the Tissot will be of the same size, and rounded in shape.
*Only 3D globe has Tissot all in the same size and round.
(Obviously..)
Distortion: EQUIVALENCE
It maintains the correct proportions of the area (size) of the 3D globe and the same area on the projected grid (2D map).
Use case: To compare sizes of area features like countries and continents.
Maintain:
Area
Distort:
Shape, Direction, Distance
Distortion: CONFORMALITY
The Tissot varies widely in size, but all are of the same round shape.
Consistent shapes indicate that this projection maintains the fidelity of angular measurements (shape) from the 3D globe to the 2D map.
Use case: Angles measured by land surveyors anywhere on the surface of the 3D globe can be plotted at the 2D map without distortion.
Maintain:
Shape
Distort:
Area, Direction, Distance
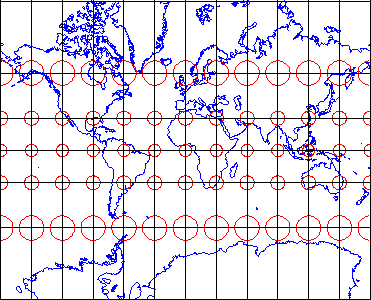
Distortion: EQUIDISTANCE
The Tissot varies in shape and size, but the north-south axis of each ellipse is the same length.
This shows that distances are true-to-scale along every meridian.
Thus it allows the distance to be measured accurately.
Use case: Measure accurately along a straight line from one or, at most, two points.
Maintain:
Distance
Distort:
Area, Shape, Direction
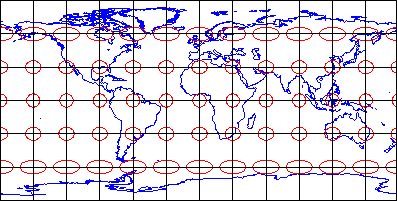
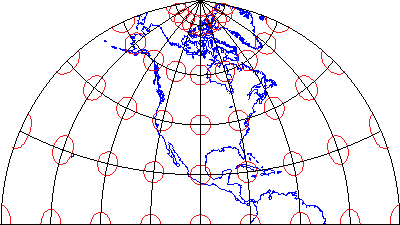
Distortion: AZIMUTHALITY
It preserves directions (azimuths) from one or two points to all other points on the map.
The Tissot varies in both shape and size, but all oriented towards the center of the projection, which is a point where direction is measured in the world, the only Tissot that is not distorted.
Use case: To plan an airline connection from one airport to all other airports.
Maintain:
Direction
Distort:
Area, Shape, Distance
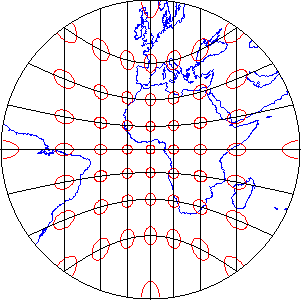
Distortion (Extra): COMPROMISE
It preserves none, but instead it seeks a compromise that minimizes distortions of all kinds.
Use case: It is often used in thematic mapping.
Maintain:
None
Distort:
All (minimal)
CRS
Coordinate Reference System
What is CRS?
- A coordinate reference system (CRS) or spatial reference system (SRS) is a coordinate-based local, regional or global system used to locate geographical entities.
- CRS defines a specific map projection, as well as transformations between different CRS.
- CRS can be referred to using a SRID integer, and can be assigned EPSG codes as CRS identifier.
- Most widely used CRS identifiers are EPSG:4326 and EPSG:3857
Types of CRS
Unprojected & Projected CRS:
-
Geographic Coordinate System (GCS), constituted by:
- Datum
- Prime Meridean
- Unit in degree
- Eg. EPSG:4326 (unprojected)
-
Projected Coordinate System (PCS), constituted by:
- GCS (GEOGCS)
- Projection (Parameters)
- Unit in metre
- Axis
- Eg. EPSG:3857 (projected)
PROJCS["WGS 84 / Pseudo-Mercator",
GEOGCS["WGS 84",
DATUM["WGS_1984",
SPHEROID["WGS 84",6378137,298.257223563,
AUTHORITY["EPSG","7030"]],
AUTHORITY["EPSG","6326"]],
PRIMEM["Greenwich",0,
AUTHORITY["EPSG","8901"]],
UNIT["degree",0.0174532925199433,
AUTHORITY["EPSG","9122"]],
AUTHORITY["EPSG","4326"]],
PROJECTION["Mercator_1SP"],
PARAMETER["central_meridian",0],
PARAMETER["scale_factor",1],
PARAMETER["false_easting",0],
PARAMETER["false_northing",0],
UNIT["metre",1,
AUTHORITY["EPSG","9001"]],
AXIS["X",EAST],
AXIS["Y",NORTH],
EXTENSION["PROJ4","+proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +wktext +no_defs"],
AUTHORITY["EPSG","3857"]]GCS :
PCS :
CRS Identifier
A Spatial Reference System Identifier (SRID) is a unique value used to unambiguously identify projected, unprojected, and local CRS.
Every CRS gets assigned a unique number, the EPSG code.
EPSG stands for European Petroleum Survey Group and is an organization that maintains a geodetic parameter database with standard codes.
Fun Fact:
Due to slow adoption by the EPSG registry back in 2000s, the Web Mercator Map Projection used by Google Maps is represented by several different names and SRIDs, including EPSG:900913, EPSG:3785, EPSG:3587 etc and the official registered by EPSG is EPSG:3857.
*900913 is GOOGLE transliterated to numbers
EPSG:4326
VS
EPSG:3857
Difference
| EPSG | 4326 | 3857 |
|---|---|---|
| CRS | Geographic Coordinate System (GCS) | Projected Coordinate System (PCS) |
| Unit | Degree | Meter |
| Area of Use | World | World (Between 85N-85S) |
| Datum | WGS84 | WGS84 |
| Distortion Type | Equidistance | Conformality |
| Scope | Used by the GPS satellite navigation system | Used by certain web mapping and visualization apps |
| Also known as | WGS84 | Web Mercator |




4326
3857
Based on the previous, what do you get?
How to determine which is best suited for data storage and visualization? And why?
Why 4326 is better used for map data storage?
- The map grid is all square and preserve distance of points along the meridean.
- GPS use EPSG:4326 to capture location in Lat/Lon (degree) which is directly from the surface of the earth.
- WGS84 is EPSG:4326. The name is just the way to identify WGS84 by using EPSG code.
- 4326 is unprojected CRS, so the location stored is in its original state from the field.
- Best suited for WFS services, since data is captured in Lat/Lon (by GPS), is best stored in Lat/Lon (EPSG:4326) and is best used in Lat/Lon for location geocoding.
Why 3857 is better used for map data visualization?
- Less cache/tiles generated. Ideal for generating map tiles since it will project the world into a square that can be subdivided evenly across zoom levels. For example one tile at zoom level 1, four tiles at zoom level 2 and so on.
- Widely used by popular web mapping applications; Google Maps, OpenStreetMap, HERE, Bing Maps etc.
- Best suited for WMS, WMTS & TMS services.
- But being popular doesn't mean it's better. It is 'controversial' used worldwide, no one dares to change. Because if you dare use other CRS, you can never correctly overlay with other popular maps. That's all, nothing wrong.
But at the moment there is a movement to propose changing the popular map visualization projection from Mercator into Gall-Peters.
Why 3857 is controversial for map visualization?
The Mercator projection increasingly inflates the sizes of regions according to their distance from the equator. This inflation results, for example, in a representation of Greenland that is larger than Africa, which has a geographic area 14 times greater than Greenland's. Since much of the underdeveloped countries lies near the equator, they appear smaller on a Mercator map and therefore seem less significant.

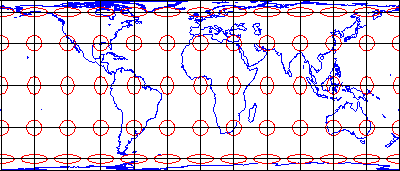
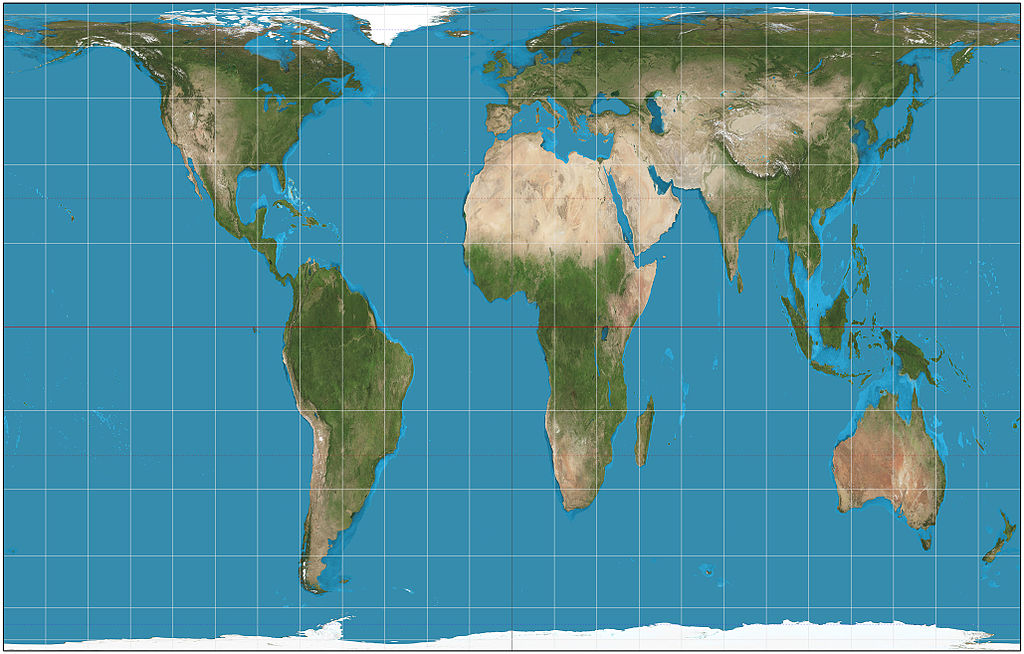
Gall-Peters Projection
This projection, by contrast, areas of equal size on the globe are also equally sized on the map. By using this projection, underdeveloped countries could be restored to their rightful proportions.
The distortion type of this projection is Equivalence (it preserves the area/size to the correct proportions on the 3D globe/earth).
Watch the video clip